对等温条件下理想气体伯努利方程的讨论

2021-03-19张国锋

物理与工程 2021年1期

周越张国锋

(1 北京林业大学理学院,北京 100083;2北京航空航天大学物理科学与核能工程学院,北京 100191)

1 问题的提出

在普通物理教材中,对伯努利方程的讨论一般仅限于理想流体的情况,即假定流体无粘性且不可压缩。与液体相比,气体的可压缩性要大得多,密度可以发生显著的变化,在流速远低于声速的条件下才能近似地将其视为理想流体[1]。要精确地定量分析气体的状态参量和流速的关系,应考虑密度变化的影响。在气体动力学中,一般把气体的流动视为等熵过程,即忽略气体和外界的热交换[2]。如果气体与热库良好地接触,膨胀和压缩过程又进行得足够缓慢,则气体的温度近似保持恒定,这时可以按等温过程处理。

在《等温条件下可压缩理想气体的伯努利方程》一文(以下简称《等》文)中基于能量守恒推导了等温条件下理想气体的伯努利方程[3],得到

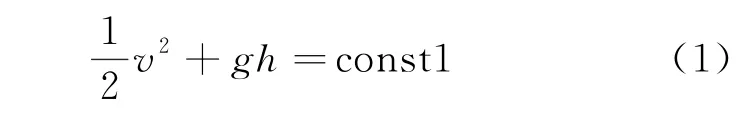
然而,式(1)的正确性是值得商榷的。理由如下:考虑理想气体在截面渐变的水平管道内做准一维定常流动,如式(1)成立则管道内气体的流速v将保持恒定。由质量流量守恒ρSv=const2可知,在v不变时气体密度与管道截面积成反比;在等温过程中,气体的压强又与密度成正比,显然管道内气体压强的纵向分布是不均匀的。设想在管道内取一个同轴的柱体,由于柱体两侧压强不同,柱体内的气体必然存在加速运动,这与流速v恒定矛盾。

2 问题分析

如图1,考虑做定常流动的理想气体中的一个截面变化的流管,流管两侧的气体压强、密度、速度和截面面积为p i、ρi、v i和S i(i=1,2)。假设经过微小时间间隔Δt后a1a2之间的气体运动到b1b2处。由定常流动的性质可知b1a2之间的气体状态没有任何变化,气体亦不可能从流管侧面逸出,因此a1b1之间的体积元ΔV1和a2b2之间的体积元ΔV2中的气体具有相同的质量Δm,在计算能量变化时只需考虑体积元ΔV1和ΔV2的能量差。《等》文中认为根据能量守恒定律,外力做功应等于ΔV1和ΔV2中气体的机械能和内能增量,即

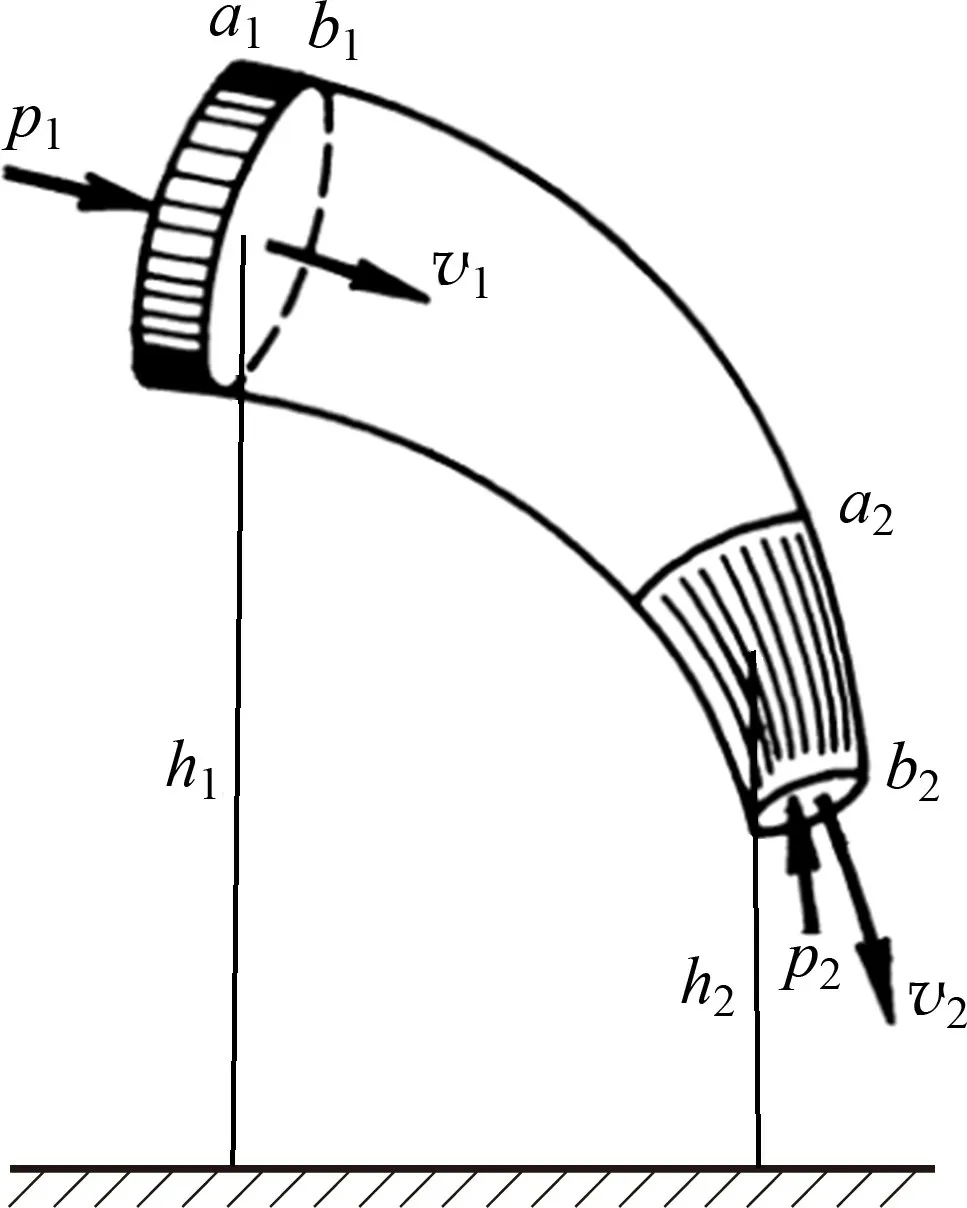
图1 定常流动的理想气体截面变化

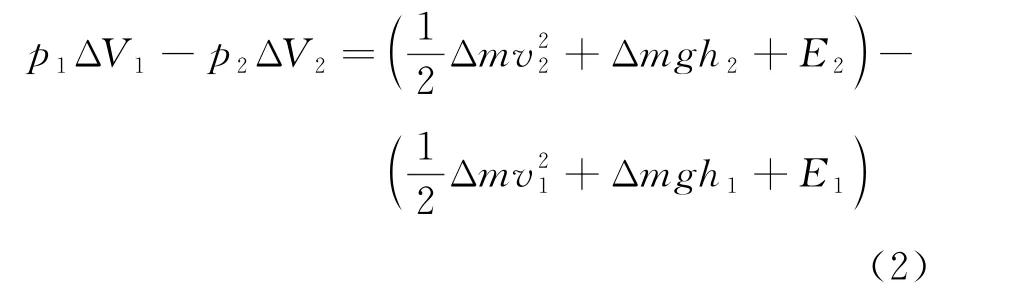
但式(2)存在两个问题:首先,理想气体的内能E是温度T的单值函数,对于等温过程,气体的内能恒定,并不存在增量;尤其重要的是,在等温过程中气体与外界存在热交换,利用能量守恒列出等量关系式时,必须将传递的热量Q考虑在内,在式(2)中因遗漏这一项而导致了错误的结果。

3 方程的推导

下面重新推导等温条件下理想气体伯努利方程的表达式。如前所述,在等温过程中理想气体的内能不变,由能量守恒,外力做功加上流动过程中气体吸收的热量应等于气体机械能的增量

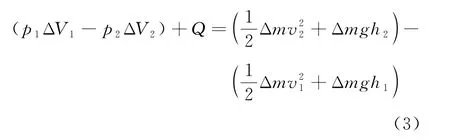
由波义耳定律p V=const3可知

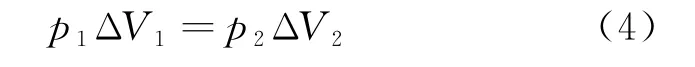
利用式(4)可将等温过程中气体吸收的热量表示为

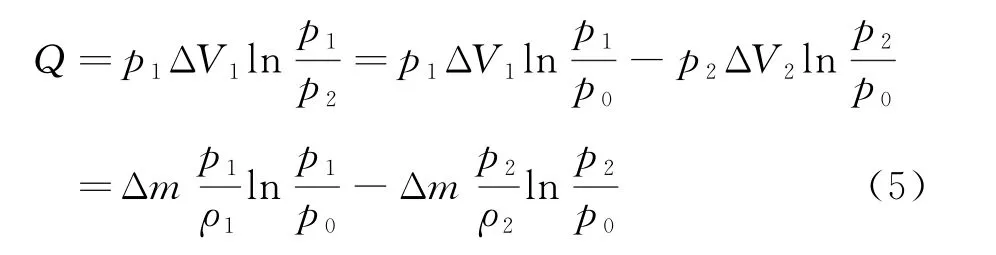
其中p0为任意常压强。将式(4)和式(5)代入式(3)并将下标相同的项移到等号同侧,可得

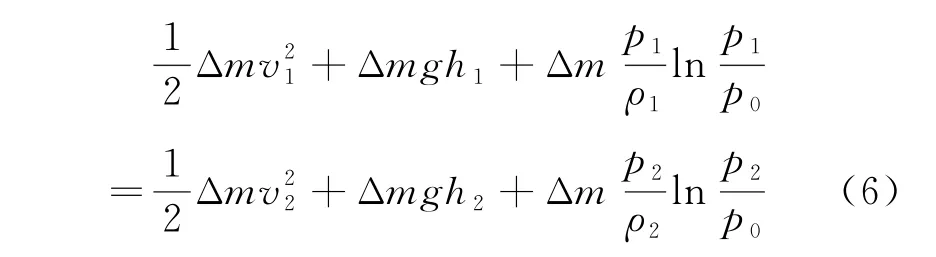
两边同时除以Δm,得

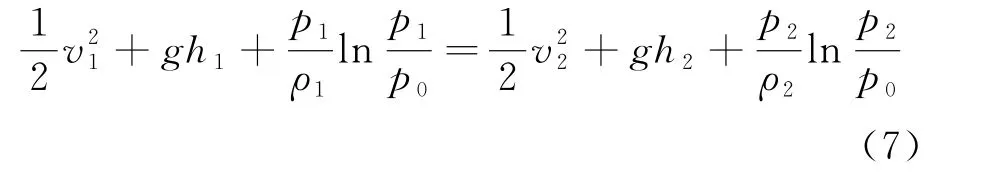
由于流管内两个截面的位置是任意的,等号两侧应共同等于一个常量,即

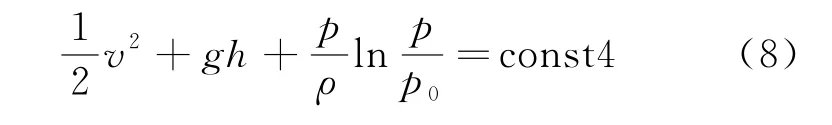
式(8)即等温条件下理想气体的伯努利方程。

利用伯努利方程的普遍性形式和等温过程的物态方程也可以导出相同的结果,简述如下。普遍形式的伯努利方程(又称伯努利积分)为[1]

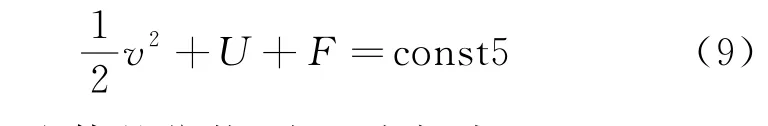
其中U为流体的位势,在重力场中U=gh;F=为压强的函数,具体形式由物态方程决定。对于等温过程,将波义耳定律表示为p/ρ=const6,则

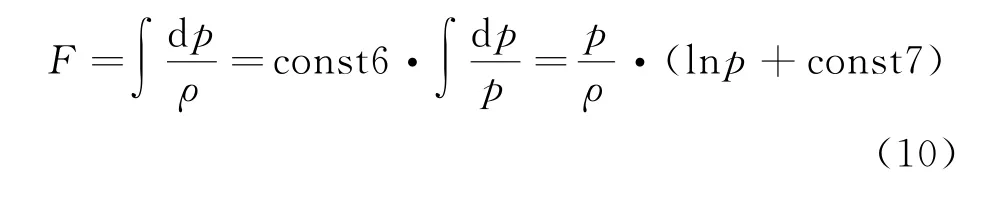
令const7=-lnp0可得

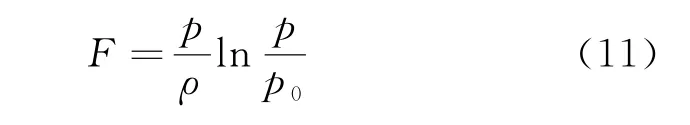
将U和F的表达式代入式(9)即得到式(8)。

利用理想气体状态方程

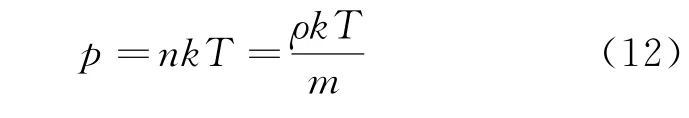
也可将式(8)等价地表示为

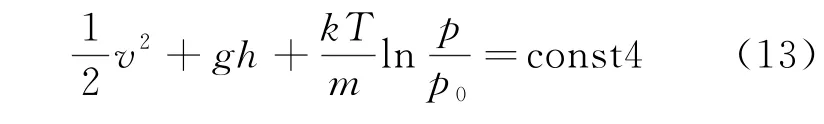
其中m为气体分子质量,k为玻耳兹曼常量。在等温过程中T为常量,利用式(12)可以更方便地说明流速与压强的关系。显然,即使在水平管道中,气体的流速也并不恒定,而是和压强有关,“流速大的地方压强小”这一规律仍然成立。还应指出的是,式(8)的成立的必要条件是气体的过程进行足够缓慢从而和外界有充分的热交换,这里的缓慢是就气体的膨胀和压缩过程而言,与流速v没有必然关系。如果流管的截面积是缓变的,即使流速较大仍然可以按等温过程处理。