考虑多类型故障的多缸液压机鲁棒容错滑模控制

贾 超 何浩成

（1.天津理工大学电气电子工程学院；2.天津市复杂系统控制理论及应用重点实验室）

当今，电液伺服系统在航空航天、船舶控制、机器人技术以及武器制造等领域得到了日益广泛的应用［1～4］。 多缸液压机由于具有结构特性优势，对其控制策略的研究也越来越多［5～7］。 由于多缸液压机具有过驱动特性，因此为系统的容错控制提供了很大的设计空间。 容错能力是考察过驱动系统稳定性和可靠性的重要方面，能够使系统部件在发生故障的情况下最大限度地满足期望的控制特性，因此开展相关研究至关重要［8，9］。

文献［10～12］分析了飞机等液压系统中由于液压缸泄漏等原因导致的执行器效能下降、中断及卡死等故障， 此类故障在液压机中也可能发生。 对于故障状态下的容错控制问题，文献［13］对一类带有螺旋桨故障的船舶动力定位系统展开了研究，文献［9］对一类考虑执行器故障的多旋翼直升机系统展开了研究，文献［14］对一类考虑执行器故障的航天器姿态稳定控制系统展开了研究，但目前针对具有冗余特性的多缸液压机容错控制方法的研究还较为少见。

受文献［9，13，14］的启发，笔者以一类多缸液压机为研究对象，在建模过程中引入多类故障模型信息，并基于Lyapunov稳定性理论，提出了一种多缸液压机滑模自适应容错控制策略，给出了严格的稳定性证明。 当执行器发生故障时，通过自适应机制在线估计故障信息，有效避免了故障信息检测模块误报所造成的影响，提高了多缸液压机的容错能力。

1 系统模型

笔者所述多缸液压机由5个活塞液压缸组成， 各液压缸分别位于滑块的4个边角位置及其中心位置。 数学模型主要分为滑块部分和液压部分［15］，其中5个活塞液压缸构成液压部分。

1.1 滑块部分模型

滑块部分的俯视图和受力示意图见文献［15］，滑块主要承受液压缸施加的力和工件的变形阻力。 各缸施加在滑块上的力用Fi（1，2，…，5）表示；工件的变形阻力被视为集中力，它可以作用在滑块下端面的任意一点，其大小、作用点与x轴的夹角以及到中心点o的距离分别记为FL、α、l。滑块中心点的位移以及围绕x、y轴的偏转角分别用xs、φx、φy表示。滑块的质量表示为mc，滑块对x、y轴的转动惯量分别用Jx、Jy表示， 位于滑块四角的活塞液压缸驱动力作用点到滑块中心点o的距离用d表示。

基于牛顿第二定律和刚体定轴转动定律，可以得出：

其中，h表示滑块上端面与下端面对角线的长度。 由于φx和φy通常较小，故假设sinφx≈φx，sinφy≈φy。

综上所述，整理式（1）～（3）可得：

当液压系统发生故障时，其实际输出驱动力可能与控制信号的期望输出驱动力不符，为此引入如下故障模型：

其中，θi为对应液压缸的效能因子，ηsi为对应液压缸未知时变有界卡死故障信号，ηi为对应液压缸的输出力，σi定义如下：

表1描述了液压缸各种故障类型的情况［16］。

其中，θi和θi分别表示第i个液压缸效能因子的下界和上界，0≤θi≤θi≤θi≤1。

上述模型与文献［7］的最大不同点在于引入了式（5），即模型的建立考虑了表1所列的多种类型故障，从而为多缸液压机高级容错控制算法的提出奠定了基础。

1.2 液压缸部分模型

假设液压缸油液密度为ρ，液压阀进口压力为ps，等效体积弹性模量为Ey，各缸进油腔的活塞面积用Ai1表示，排油腔的活塞面积用Ai2表示，进油腔与排油腔的容积分别表示为Vi1与Vi2， 各缸进油腔与排油腔的压强分别表示为pi1、pi2，每个液压阀的阀口流量系数为Cdi，每个液压阀的阀口面积为ui。

根据液压缸的流量方程和伺服阀的阀口流量公式，可以列出每个液压缸的进油腔和排油腔的压力动态特性：

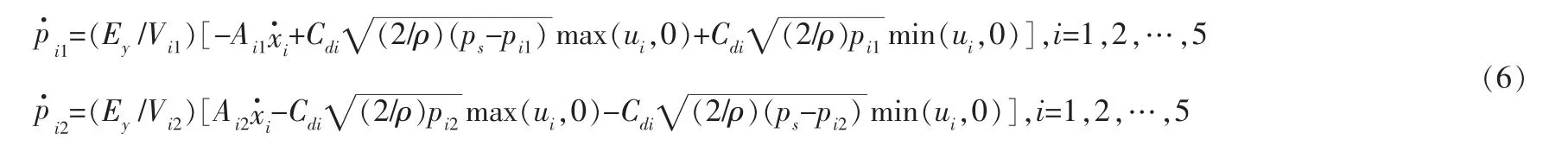
式（4）～（6）共同构成了带有故障信息的多缸液压机数学模型。 综合上述系统可以看出，该模型考虑了液压缸的多种类型故障，且系统输入多于系统输出，各缸压力的变化具有明显的非线性特性。 因此，该系统为考虑多类故障因素的非线性过驱动系统。

1.3 控制目标

笔者的控制目标是针对多缸液压机设计自适应滑模容错控制律，使多缸液压机在执行器失效、中断及卡死等故障情况下依然能够实现高精度的位移跟踪和调平。

2 控制器设计

2.1 自适应滑模控制器设计

为了保证容错控制算法的提出，引入如下假设。

假设1 非参数卡死故障ηs为分段连续有界方程，即存在未知正常数ηs，使得‖ηs‖≤ηs。

假 设2 在 任 意 故 障 类 型 下，rank（Bθ）=rank（B）=3，rank（*）代表矩阵*的秩。

首先，给出误差向量的定义：

其中，e=［e1，e2，e3］T，xd=［xsd，φyd，φxd］T为x的期望值。

滑模面设计为：

引理1［13］对于行满秩的矩阵B，一定会存在一个正标量μ， 使得在任意故障类型下， 不等式BθBT≥μBBT≥成立。

2.2 执行器控制律设计

采用分散滑模控制算法设计执行器控制律［7］。

由式（6）可以得到如下的最终控制律：

定理1 对于式（4）～（6）描述的考虑执行器多类故障及干扰的非线性系统， 满足假设1、2和式（15）条件，若采用式（8）的滑模面，控制律由式（9）～（13）、（16）给出，则在存在外部有界扰动和执行器故障的情况下，依然可以保证闭环容错系统所有信号一致有界。

证明 选取如下形式的Lyapunov函数［13］：

3 仿真分析

为了对笔者所提控制算法的跟踪和调平性能进行验证，并评估其容错能力，以第1节所述多缸液压机为对象进行仿真研究，并与文献［7］所提多缸液压机的控制算法进行对比。

液压模型参数（其中下角标i=1，2，3，4）为：mi=5.84×103kg；m5=5.84×104kg；mc=5×105kg；Jx=1.764×106kg·m2；Jy=2.534×106kg·m2；c=9.247m；d=5.8825m；ρ=900kg/m3；Ai1=1.5m2；A51=6.35m2；Ai2=0.23m2；A52=1m2；Vi1=1m3，V51=10.6m3，Vi2=0.3m3；V52=4m3；ps=31.5GPa。

负载力作用点参数选为l=0.25m，α=π/3， 该力大小随滑块下行而改变。 系统运行初始时刻滑块并未接触到负载，负载力值为0，滑块下降5mm时接触到负载， 受到一个力值与位移深度成正比的变形阻力，该力在达到最大值2×108N后保持恒定。

控制器参数为：c1=c2=c3=3000；k1=2×106；k2=1000；k3=1000；λi=0；δi=100；ε1=200；ε2=30；ε3=30；μ=0.09；r1i=0.02；r2i=0.005；r3k=2；r4i=0.05。

3.1 单液压缸故障

3.1.1 失效故障

为了验证笔者设计控制器对液压缸失效故障的容错能力，假设5s后，第3个液压缸失效50%，与文献［7］进行对比，仿真结果如图1～4所示。 定义Δ1=x1-x3，Δ2=x2-x4， 以便描述滑块的调平误差，衡量系统的调平精度。 由图1可以看出两种控制器皆能实现高精度的位置跟踪， 但图2～4的曲线说明：当系统第3个液压缸效能降低50%时，笔者设计控制器的调平精度更高，可以更好地抑制液压缸故障产生的影响，具有更好的容错能力。 图5为笔者设计控制器的输出曲线，可以看出，控制器在液压缸发生故障时做出了适当的调整， 从而提高了系统在故障状态下的调平精度和容错能力。

图1 位移跟踪曲线

图2 绕y轴偏转角响应曲线

图3 绕x轴偏转角响应曲线

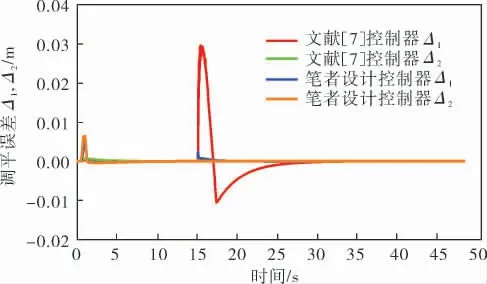
图4 调平误差曲线

图5 控制器输出曲线

表2为执行器发生失效故障时， 笔者设计控制器与传统控制器的调平性能对比， 表中的eφ=max｛φy，φx｝表示偏转角最大误差，eΔ=max｛Δ1，Δ2｝表示调平最大误差。

表2 调平性能对比

3.1.2 卡死故障

为了验证笔者设计控制器对液压缸卡死故障的容错能力，假设15s后，第2个液压缸发生卡死故障，所选卡死信号为7×105（1+sint），与文献［7］控制器进行对比，仿真结果如图6～9所示。 由图6可知，当执行器出现卡死故障时，两种控制器都能实现良好的位置跟踪，但是观察图8、9可以发现，文献［7］控制器在调平方面产生了很大的波动，笔者设计控制器依然能以较快的速度实现调平控制。

图6 位移跟踪曲线

图7 绕y轴偏转角响应曲线

图8 绕x轴偏转角响应曲线

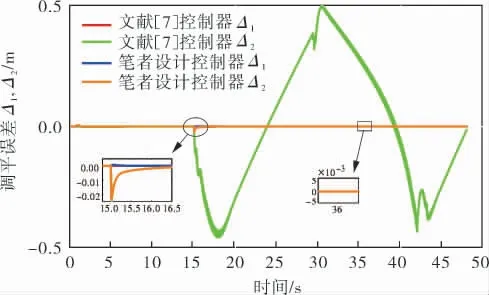
图9 调平误差曲线

3.2 多液压缸故障

假设第9s后， 第4个液压缸效能降低为85%，在此基础上，当系统运行至第15s时，第1个执行器同时出现中断故障，仿真结果如图10～13所示。 第9s出现失效故障时，对系统的影响并不明显，但从各图的局部放大图依然可以观察到失效故障对系统的影响和系统的调整过程；当系统在第15s又出现中断故障时， 由图11～13可知该故障对系统产生了明显的影响，但笔者设计控制器依然能使系统以较快速度进行调整，实现位移跟踪与调平控制。

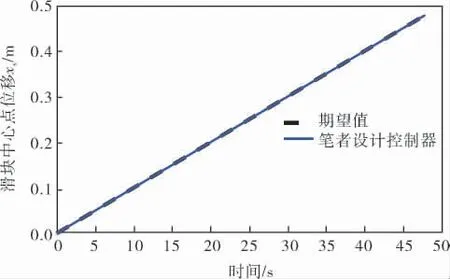
图10 位移跟踪曲线

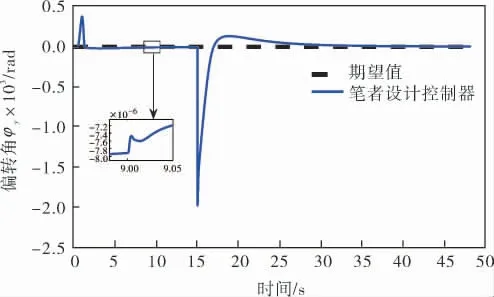
图11 绕y轴偏转角响应曲线

图12 绕x轴偏转角响应曲线

图13 调平误差曲线

以上通过在单液压缸发生多类型故障以及多液压缸同时发生不同类型故障的情形下，对控制器性能的对比与测试，充分说明了笔者设计控制器具有较强的容错能力，与文献［7］控制器相比具有明显的优越性。

4 结束语

笔者针对一类多缸液压机的鲁棒容错控制问题展开了研究。 首先建立了考虑多种类型故障的多缸液压机数学模型。 在此基础上，结合自适应机制， 提出了一类自适应滑模容错控制算法。该算法可以通过自适应机制在线估计未知外部扰动，且在故障发生时无需依赖故障信息检测模块（FDI），仍能使多缸液压机具有高精度的位置跟踪和调平能力。通过Lyapunov稳定性分析，证明了所提控制算法的一致稳定性。 仿真实验表明，所提控制方法能够实现高精度的位置跟踪和调平，且对多种类型故障具有较强的容错能力。 考虑执行器物理约束下的多缸液压机容错控制是值得进一步研究的方向。