数据驱动的变速器传感器故障诊断方法
2021-03-19
(同济大学汽车学院,上海 201804)
安全一直是车辆领域的主题之一,作为车辆动力传动部件的变速器对于安全驾驶有着至关重要的作用。传感器作为获取变速器信号的器件,是变速器与控制器之间通信的重要桥梁,传感器的正常与否直接影响变速器的性能,所以对于传感器的故障诊断至关重要。
传感器的故障诊断方法有3 种,分别为基于模型、基于规则与数据驱动的故障诊断方法[1-2]。
在能够获得系统精确解析模型的情况下,基于模型的故障诊断方法是最直接有效的,但对于变速器这样的复杂系统,精确的解析模型一般难以获得。此外,模型的不确定性、系统的非线性特性等都会对诊断结果产生很大影响。Lee[3]使用奇偶方程法对电动助力转向系统中的传感器进行故障诊断,由于模型存在不确定性,因此设置自适应阈值来提高故障诊断的鲁棒性,但该方法的对象是线性时不变系统,对于变速器这样的非线性时变系统而言适用性较差。Wang等[4]研究了多输入-多输出非线性模型的故障诊断方法,通过将该模型转化为多个一维的线性等效模型来处理非线性问题,简化了建模工作量,但没有分析系统内部结构对故障诊断产生的影响,这在模型简化时是必须要考虑的。
基于规则的故障诊断方法要求积累足够的故障原因与故障表象的先验知识,然后将知识转化为推理规则。运用故障树分析(FTA)、失效模式和效果分析(FMEA)等方法实现故障诊断,优点是规则非常容易修改,缺点是知识获取困难。Yang 等[5]通过FTA 方法对传感器故障进行诊断,仅考虑2 种故障规则就多达102条,工作量很大。变速器系统复杂,传感器数量多,在FAT 方法下故障规则可达到300多条。Zhang 等[6]运用概率分布方法对知识中的不确定性进行了处理,但是只适用于简单系统。
数据驱动的故障诊断方法不需要建立精确的解析模型,也不需要足够的先验知识,只需要通过对传感器信号的变化特性进行分析,再结合人工神经网络、主成分分析等识别算法就可完成对传感器故障的诊断。范立维[7]和Ji等[8]通过小波包分析、集成经验模态分解等对传感器信号进行特征值提取,再通过支持向量机算法实现对传感器故障的识别,但只考虑了传感器信号稳定时情况。Wang 等[9]不直接分析传感器信号,而是通过对传感器信号残差进行分析来实现故障诊断,动态和稳态时均有较好效果。
目前基于模型的故障诊断方法大多只针对传感器进行建模,不能从变速器系统的角度出发进行故障诊断,基于规则的故障诊断方法多见于企业,企业依靠多年的行业经验能够建立比较全面的诊断规则,数据驱动的故障诊断方法随着人工智能的兴起逐渐成为研究热点,越来越多的学者投入其中。变速器是一个复杂的系统,由众多零部件组成,而且工况变化多端,传感器输出呈现动态性强、噪声多等特点,基于模型和基于规则的变速器传感器故障诊断方法耗时长、难度大,不能实现快速有效的故障诊断。针对以上问题,提出以小波包变换(WPT)和概率神经网络(PNN)为基础的数据驱动的变速器传感器故障诊断方法。
1 数据驱动的故障诊断方法
数据驱动的变速器传感器故障诊断方法流程如图1 所示。以离合器油压传感器故障诊断为例,驾驶员通过加速踏板和制动踏板控制车辆行驶,获取车辆行驶过程中的整车及变速器数据。油压传感器的实际输出为y,从获取的数据中选取轮速、行驶挡位、预换挡位、输入轴转速、发动机转速、同步器位置作为油压传感器模型的输入。使用逐步回归算法建立油压传感器模型,模型的输出为,油压传感器的实际输出与模型输出相减得到油压传感器信号的残差序列Δy,将Δy通过WPT 分解,计算每个节点的香农熵作为特征值,然后使用PNN对特征值的类别进行识别,从而完成故障的诊断工作。

图1 数据驱动的变速器传感器故障诊断方法流程Fig.1 Flow chart of data-driven diagnosis method for transmission sensors
1.1 逐步回归算法
逐步回归算法的基本思想是通过计算自变量对因变量贡献度的大小,逐步引入对因变量贡献显著的自变量,并剔除对因变量贡献不显著的自变量,一直重复此过程,直到所有对因变量贡献显著的自变量都已被引入,所有对因变量贡献不显著的自变量都已被剔除,这样就可以建立起最优的多元线性回归模型[10]。衡量自变量对因变量贡献度的指标是偏回归平方和。假设逐步回归算法的输入样本为n×(m-1)的矩阵,n代表样本数,(m-1)代表自变量的个数,为统一表达,将输入与因变量组成n×m的矩阵x,最后一列代表因变量。为了消除量纲差异带来的影响,需要对输入进行标准化处理,标准化的公式如下所示:

式中:xi,j、分别是标准化前、后的第i个样本中第j个变量(包括自变量与因变量,下同)的值,i=1,2,…,n,j=1,2,…,m;是第i个样本的算术平均值。第j个变量的偏回归平方和定义为

式中:rj,m是第j个自变量与因变量的相关系数;rj,j是第j个自变量的自相关系数。相关系数描述自变量与因变量之间的相关程度,表示为
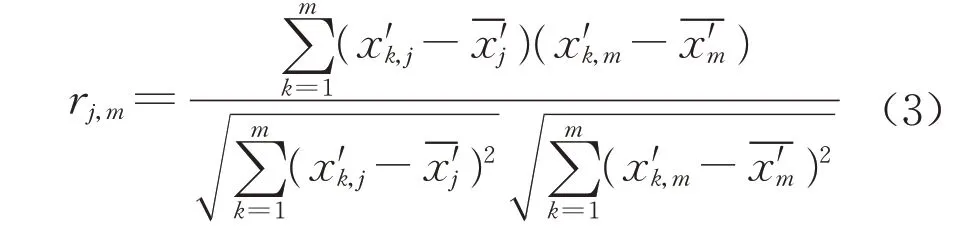
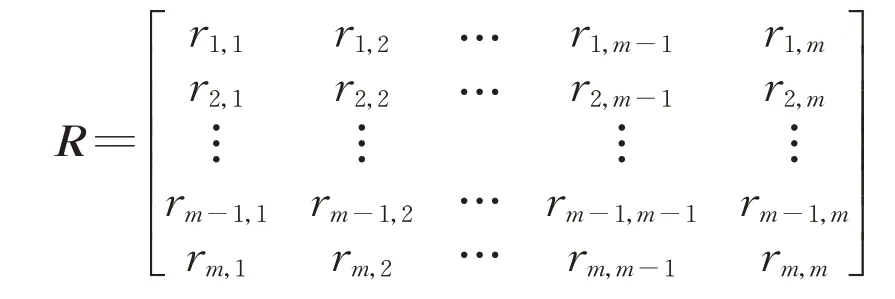
选择未被引入的自变量中对因变量贡献最大的自变量作为待引入的自变量,选择已被引入的自变量中对因变量贡献最小的自变量作为待剔除的自变量,根据F检验值决定待选的自变量是否被引入或剔除。F检验值计算式如下所示:

式中:Fin,l、Fex,l为第l次重复时待引入与待剔除自变量的检验值;μin,l、μex,l为第l次重复时待引入与待剔除自变量的偏回归平方和;rm,m,l-1、rm,m,l为第(l-1)、l次重复时的自相关系数。设Fa是F检验的临界值,当Fin,l≥Fa时,将待选自变量引入,当Fex,l<Fa时,将待选自变量剔除。每次完成自变量的筛选之后根据求解求逆变换原理进行相关系数矩阵的更新,如下所示:
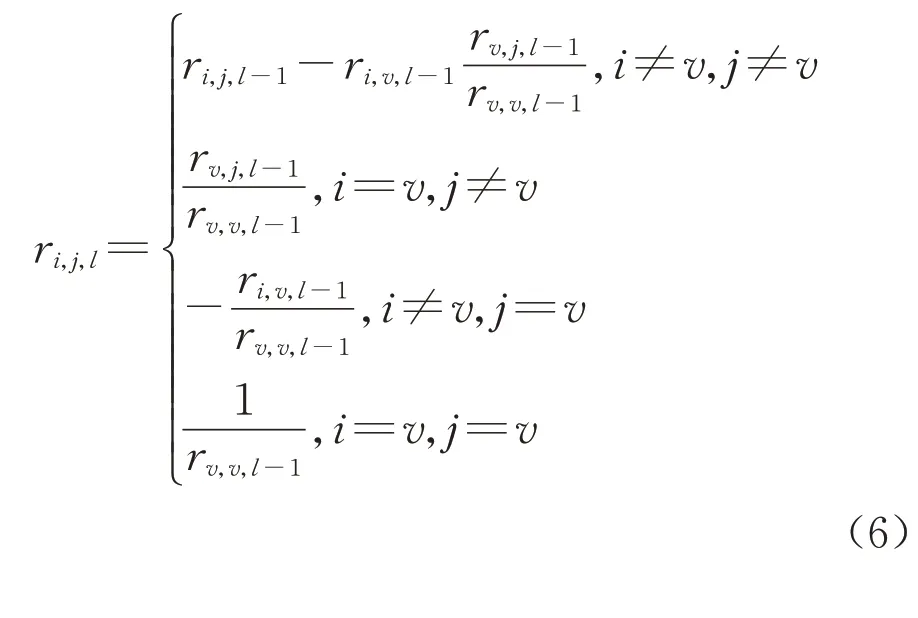
式中:v是待引入自变量的索引。
1.2 WPT-PNN
残差序列经过WPT 分解之后提取香农熵作为特征值,然后用PNN 对特征值进行识别,从而对故障做出诊断。WPT-PNN结构如图2所示。

图2 WPT-PNN结构Fig.2 Structure of WPT-PNN
1.2.1 WPT
WPT是在离散小波变换的基础上发展而来,通过同时对信号的高频部分和低频部分进行分解,确保信号的信息不会丢失。
WPT 的基本原理是将信号通过低通滤波器和高通滤波器后,再进行下采样过程,信号被分解为低频部分和高频部分。低频部分被称为近似系数,高频部分被称为细节系数,近似系数和细节系数统称为节点。将每个节点继续通过低通滤波器和高通滤波器后,再进行下采样,得到下一层节点,不断重复此过程,直至达到预定的分解层数[11]。假设得到的残差序列Δy=(Δy1,Δy2,…,Δyu),u代表采样点数。分解层数为J,则得到2J个节点,节点的长度d=u/2J。近似系数和细节系数的计算式分别为

式中:lJ、hJ分别是第J层的近似系数和细节系数;G、H分别是低通滤波器和高通滤波器,由小波函数构成;aJ-1是第(J-1)层的节点值。
Δy经过WPT 分解后,提取节点的香农熵作为特征值。香农熵是度量信号不确定性大小的指标,也是WPT 常用的特征之一。香农熵的计算式如下所示:
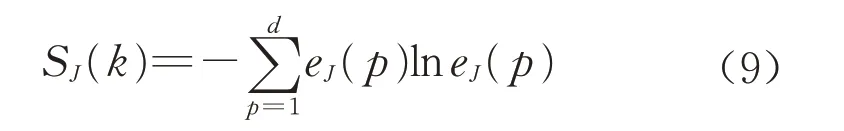
式中:SJ(k)是第J层第k个节点的香农熵,k=1,2,…,2J;eJ(p)是该节点中第p个数据点的能量占比。eJ(p)的计算式如下所示:
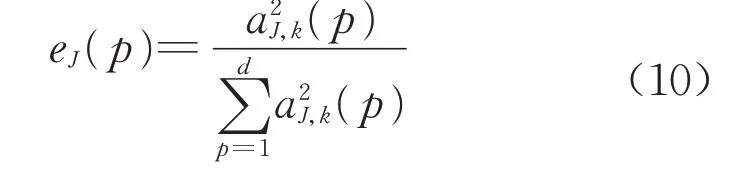
式中:aJ,k(p)是第J层第k个节点中第p个数据点的值。由式(10)可以得到香农熵的特征向量s=[s1,s2,…,s2J]。
1.2.2 PNN
PNN 以径向基神经网络(RBF)为基础,采用贝叶斯决策规则为分类依据,克服了反向传播神经网络(BPNN)局部最优问题以及RBF对径向基函数敏感问题,训练容易,收敛速度快,非常适用于实时处理[12]。PNN的一般结构如图3所示。
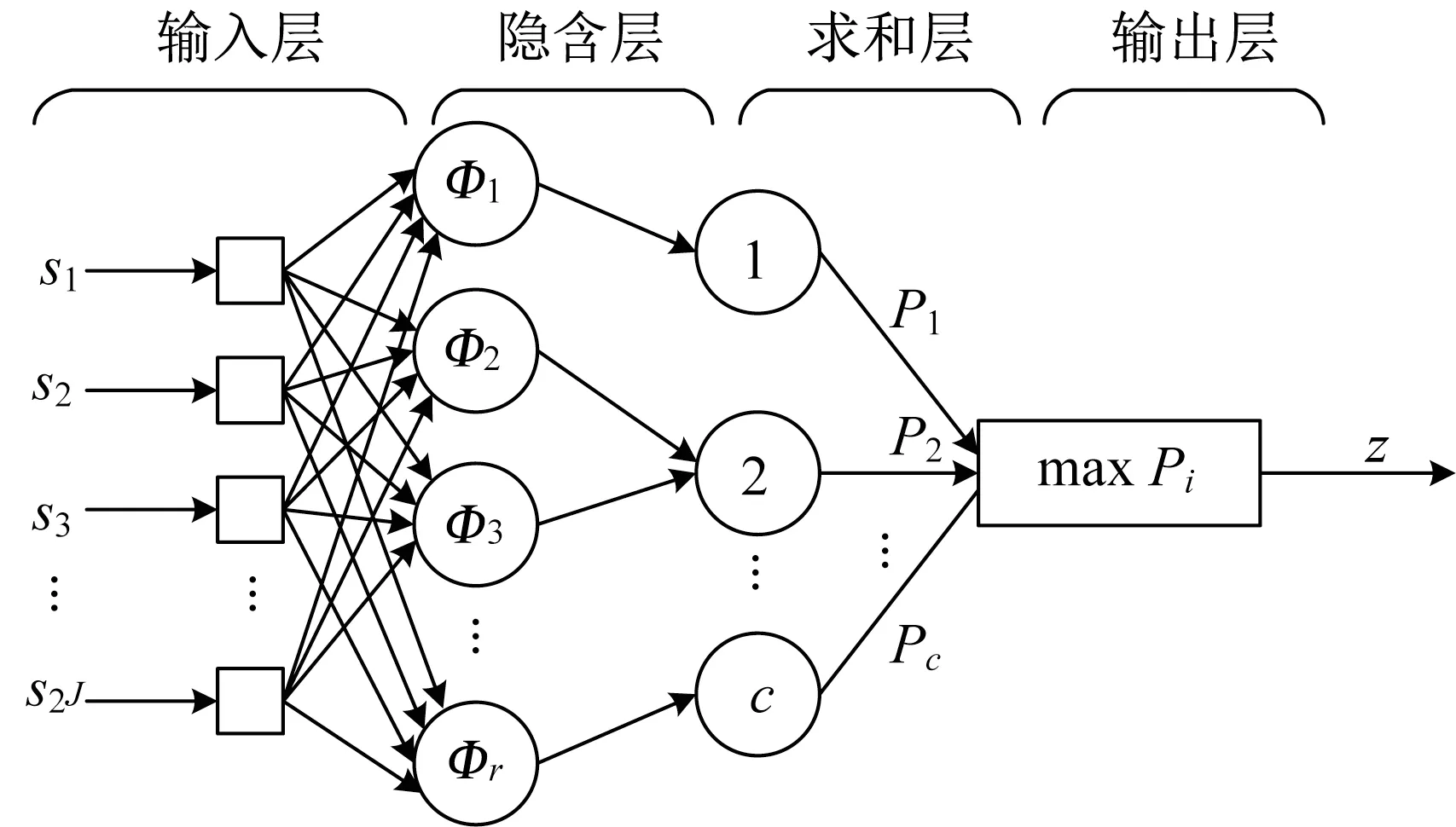
图3 PNN结构Fig.3 Structure of PNN
PNN 包含4 层结构,输入层用于接收来自样本的值,神经元个数与输入向量长度相同,隐含层为径向基层,激活函数为高斯核函数。隐含层有r个神经元,第q个神经元的输出
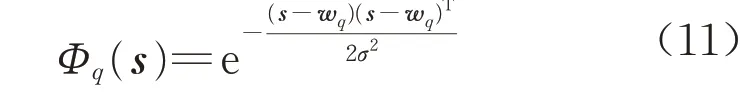
式中:Φq(s)是第q个隐含层神经元的输出,q=1,2,…,r;σ是平滑因子,对网络性能起着至关重要的作用;wq是第q个隐含层神经元的权重向量。求和层对隐含层的输出做加权平均,每一个求和层神经元代表一种类别。求和层共有c个神经元,第b个神经元的输出结果

式中:Pb是第b个类别的加权输出,b=1,2,…,c,其中c是样本类别数;L是指向第b个类别的隐含层神经元数。输出层依照贝叶斯决策规则决定输出的类别,贝叶斯决策的目的是使误判的风险降到最小。定义风险函数
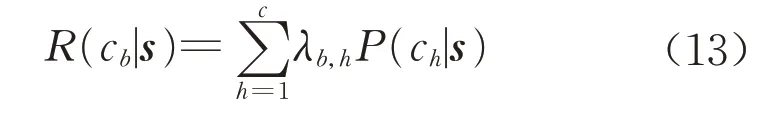
式中:R(cb|s)是将输入向量s判断为第b个类别的风险;λb,h是把类别h判断为类别b的损失;P(ch|s)是将输入向量s判断为类别h的条件概率,对应求和层中第h个神经元的输出。对λb,h定义,分类错误的损失为1,分类正确的损失为0,则式(13)就变成R(cb|s)=1-P(cb|s),要使R(cb|s)最小,P(cb|s)最大,则输出层取最大求和层输出对应的类别,即:
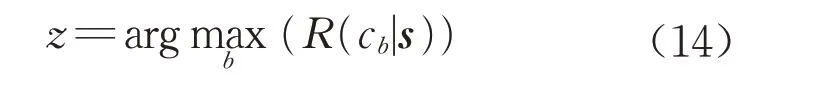
2 方法验证
2.1 数据采集
为验证本方法,使用硬件在环仿真试验台进行传感器故障数据的采集。硬件在环仿真试验台由宿主机、目标机、执行器(电磁阀)、输入(制动踏板和加速踏板)、控制器等组成,如图4 所示。宿主机中储存车辆模型以及变速器的控制策略,试验车辆为某款长安CS 系列SUV,搭载双离合器式自动变速器(DCT)。通过C 语言编译器和背景调试模式(BDM)设备将宿主机中的控制策略存储到变速器控制单元(TCU)中,TCU通过数据采集与转换板卡与目标机通信,并驱动电磁阀工作。目标机包含车辆的实时运行环境(RTW),并可以实时显示运行结果,通过TCP/IP 协议与宿主机通信。采样频率设为100 Hz,试验工况为30%恒定油门起步,分别在起步、升挡过程、在挡稳定行驶、降挡过程中注入故障。在过程中的随机时间点注入故障,注入故障后5 s停止数据采集。

图4 硬件在环仿真试验台架构Fig.4 Structure of hardware-in-the-loop platform
传感器典型故障有偏差、冲击、堵塞等[13-14],以奇数离合器油压传感器为例,该传感器属于电阻应变片式传感器。图5展示了车辆稳态行驶时某些传感器典型故障的具体表现形式(1 bar=0.1 MPa)。偏差故障设置为在正常值基础上增加10%,冲击故障的冲击大小设置为最大传感器测量值,持续时间为2 个采样周期,堵塞故障的恒值输出设置为故障发生前一时刻的传感器测量值。每种故障采集样本80 组,取发生故障前后的350 个数据点作为样本点。
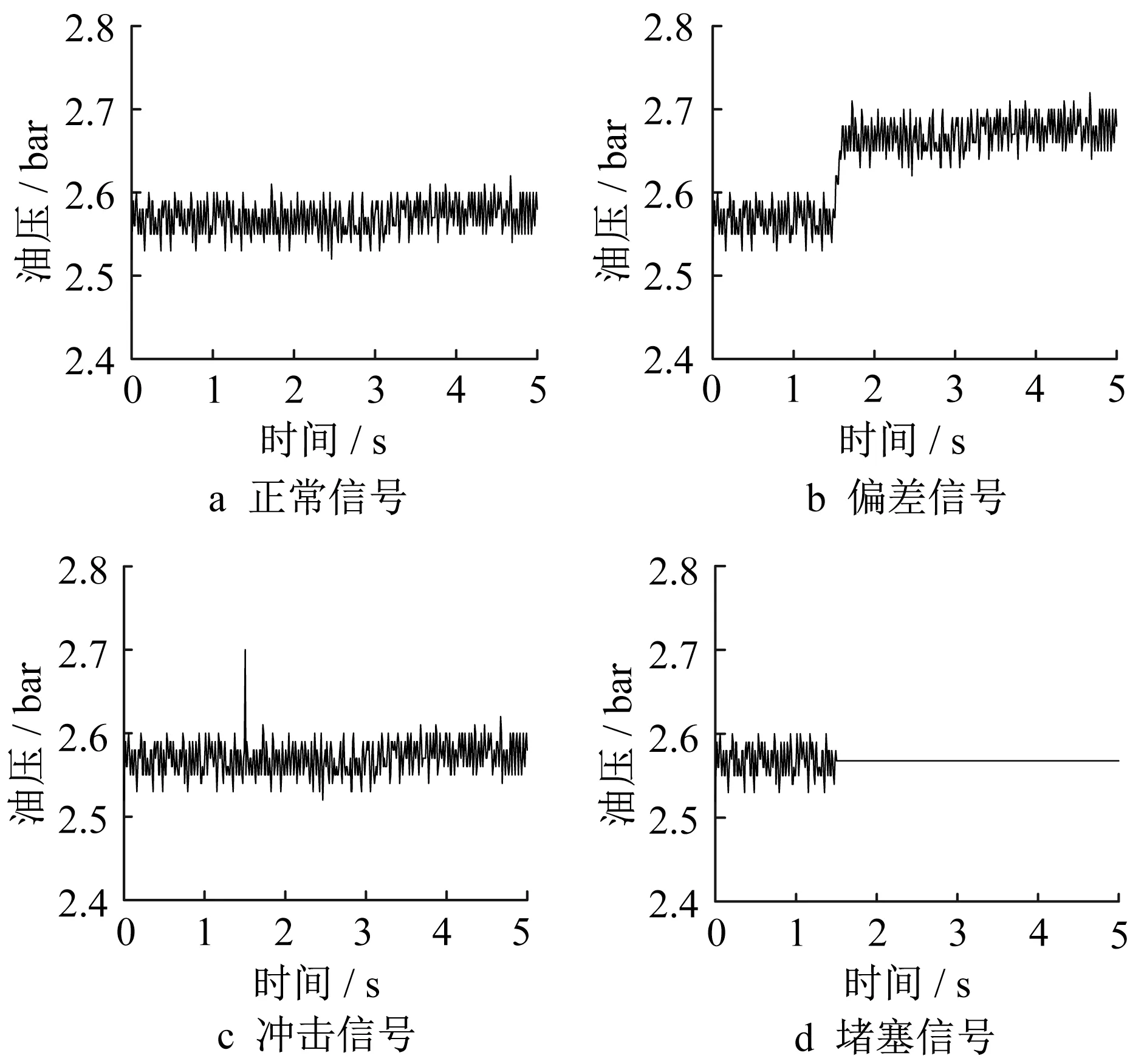
图5 传感器典型故障表现形式Fig.5 Typical signal modes of sensor faults
2.2 逐步回归模型
运用第1.1 节中介绍的逐步回归算法建立传感器模型。因为变速器的其他信号与目标传感器输出信号之间存在强非线性关系,而逐步回归算法属于线性回归算法,所以必须要对原始的变速器信号进行处理才能使用逐步回归算法。通过取倒数、相乘、平方等方式对原始信号进行重组。根据DCT 工作原理[15],对于奇数离合器油压传感器模型,原始输入选为发动机转速、奇数输入轴转速、偶数输入轴转速、行驶挡位、预换挡位、轮速、同步器位置,重组后的输入为行驶挡位与发动机转速的乘积、发动机转速的倒数、转速的平方值等。通过逐步回归得到奇数离合器油压传感器模型,如下所示:
式中:为模型输出;v1为发动机转速;v2为偶数输入轴转速;v3为预换挡位;v4为轮速;v5为发动机转速的倒数;v6和v7分别为奇数输入轴转速与行驶挡位乘积及其倒数;v8和v9分别为偶数输入轴转速与行驶挡位乘积及其倒数;v10为轮速与行驶挡位的乘积;v11为轮速与预换挡位的乘积;v12为偶数离合器油压。奇数油压传感器输出与奇数油压传感器模型输出的对比结果如图6所示。从图6可以看出,传感器模型能够较好地跟踪实际值,最大误差在0.3 bar左右,并且只出现在换挡时油压下降的过程中,其余过程均能控制在0.2 bar 以下,跟踪精度达到了92%,证明了传感器模型的有效性。
2.3 诊断结果分析
正常与故障下残差序列如图7所示。为了消除残差幅值差异带来的影响,将残差进行[-1,1]区间的归一化处理。归一化公式如下所示:

根据第1.2 节提出的方法,将从硬件在环仿真试验获得的传感器信号与传感器模型的输出相减,得到残差序列,残差序列经过WPT分解后提取香农熵作为特征值。小波函数选为离散Meyer 函数,分解层数选为3层,则特征向量的维度为8,用PNN对特征向量进行识别,各层神经元个数分别为8、240、4、1。将样本进行随机划分,75%的样本用于训练,25%的样本用于测试,如表1所示。

图7 传感器正常与故障下的残差序列Fig.7 Residual sequence of normal and faulty sensors
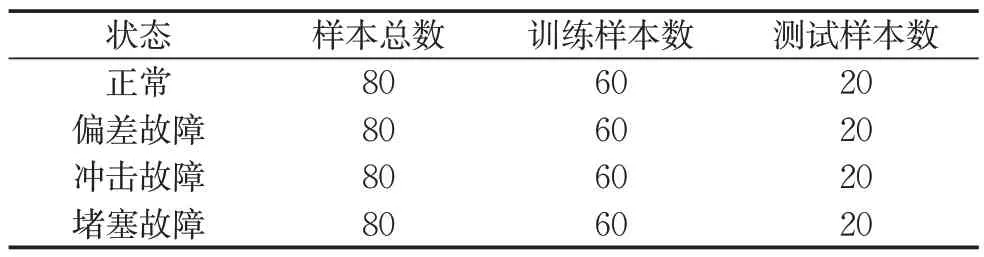
表1 样本划分Tab.1 Division of samples
平滑因子σ的大小对PNN性能有着至关重要的影响。σ较小时,径向基函数曲线形状较窄,只有与权值向量距离很近的输入才能获得较大输出,其他的输入对分类结果的影响很小;σ较大时,径向基函数曲线形状较宽,与权值向量距离较远的输入也会对分类结果产生一定的影响。为了获得尽可能高的诊断正确率,σ取值应适中,既不能太大,也不能太小。图8展示了PNN在某次训练过程中诊断正确率随σ变化的曲线。从图8 可以看到,诊断正确率随σ的增大呈现先增大后维持不变最后减小的趋势,在σ=3~16时,诊断正确率达到了最大。为了使PNN在不同的样本划分情况下仍能保持较高的诊断正确率,σ应取大些,本研究中的σ取为8。
PNN 的诊断结果如图9 所示,图9 同时展示了BPNN 和RBF 的诊断结果,以作对比。BPNN 网络层数为4层,各层神经元个数分别为8、10、4、1;RBF网络层数为3 层,各层神经元个数分别为8、240、1。在图9 的纵坐标中,1 代表正常信号,2 代表堵塞信号,3 代表偏差信号,4 代表冲击信号,在横坐标中,1~20 样本数是正常信号,21~40 样本数是堵塞信号,41~60 样本数是偏差信号,61~80 是冲击信号。根据图9统计每种类别的诊断结果,如表2所示。
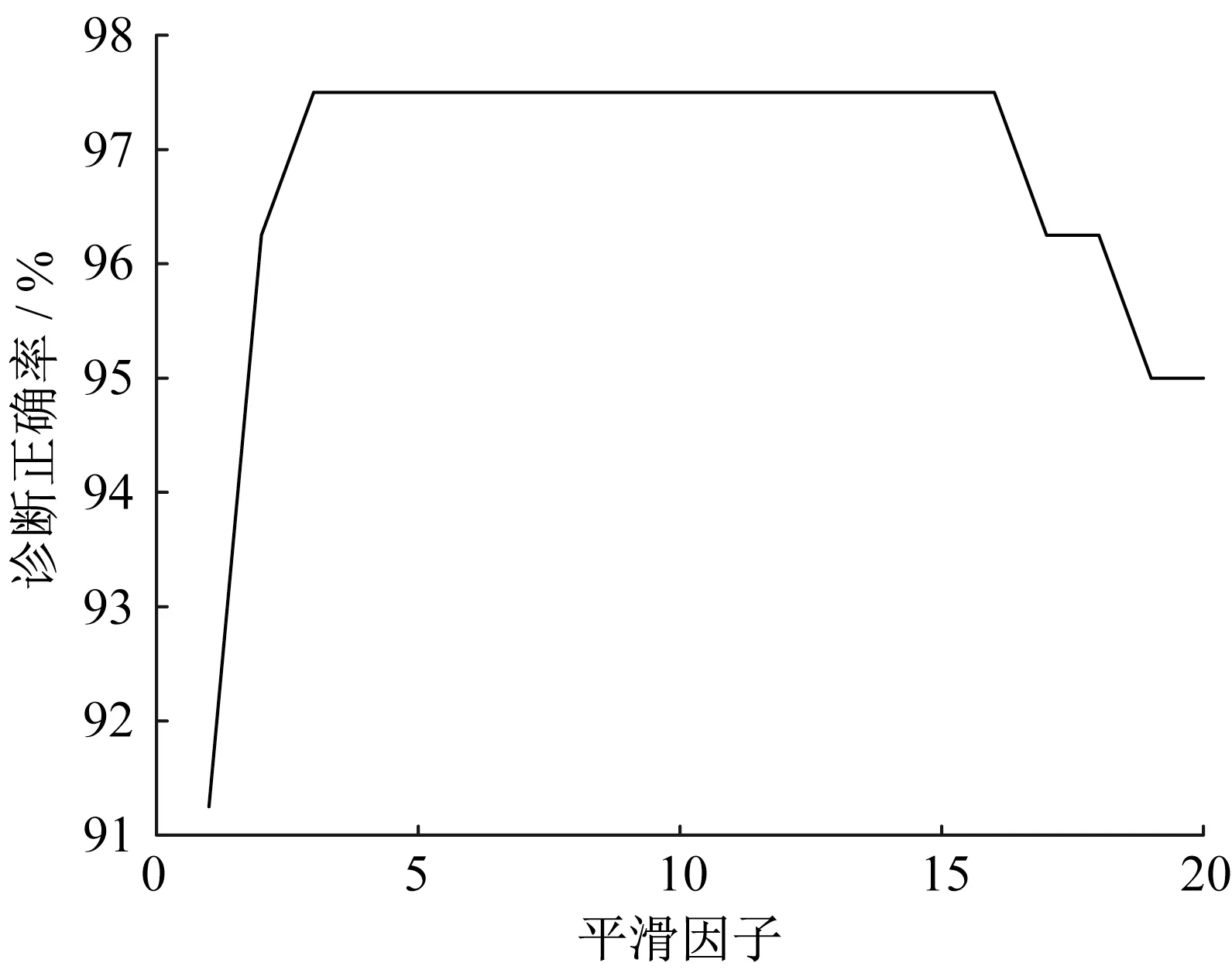
图8 诊断正确率随平滑因子变化的曲线Fig.8 Curve of diagnostic accuracy as a function of smoothing factor
由图9及表2可以看到,WPT-PNN只对一个堵塞故障识别错误,其余均能正确识别,而WPTBPNN 和WPT-RBF 的识别错误数均大于WPTPNN,诊断正确率要低于WPT-PNN,这就说明WPT-PNN的诊断性能优于其他2种方法。由于样本是随机划分为训练集和测试集,每次划分的结果是不同的,为了进一步探讨不同的划分结果对诊断正确率的影响,对样本进行5次随机划分,记录每次划分的诊断正确率。诊断正确率α的计算方法如下所示:

图9 不同方法下的诊断结果对比Fig.9 Comparison of diagnosis results between different methods
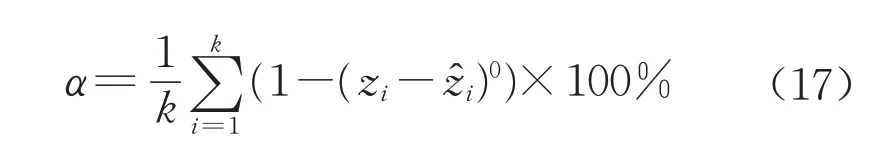
式中:zi代表实际样本类别;代表诊断得出的样本类别;k为测试样本数,k=80。

表2 不同诊断结果对比Tab.2 Comparison of diagnostic results between different methods
诊断正确率结果如表3 所示。从表3 看到,WPT-PNN不仅诊断正确率高,诊断结果稳定,还对数据有较强的适应性,WPT-BPNN 的诊断正确率较低,而且波动较大,稳定性不高,WPT-RBF 虽然诊断结果较稳定,但诊断正确率要低于WPT-PNN。相比其他2 种方法,WPT-PNN 具有较大的优势。为了进一步验证该方法的适用性,对DCT中的奇数轴转速传感器和偶数轴转速传感器进行故障诊断,数据采集、样本划分和方法的参数设置与上述相同。图10展示了2种传感器的故障诊断结果。

表3 不同样本划分下的诊断结果Tab.3 Diagnostic results for different divisions of samples
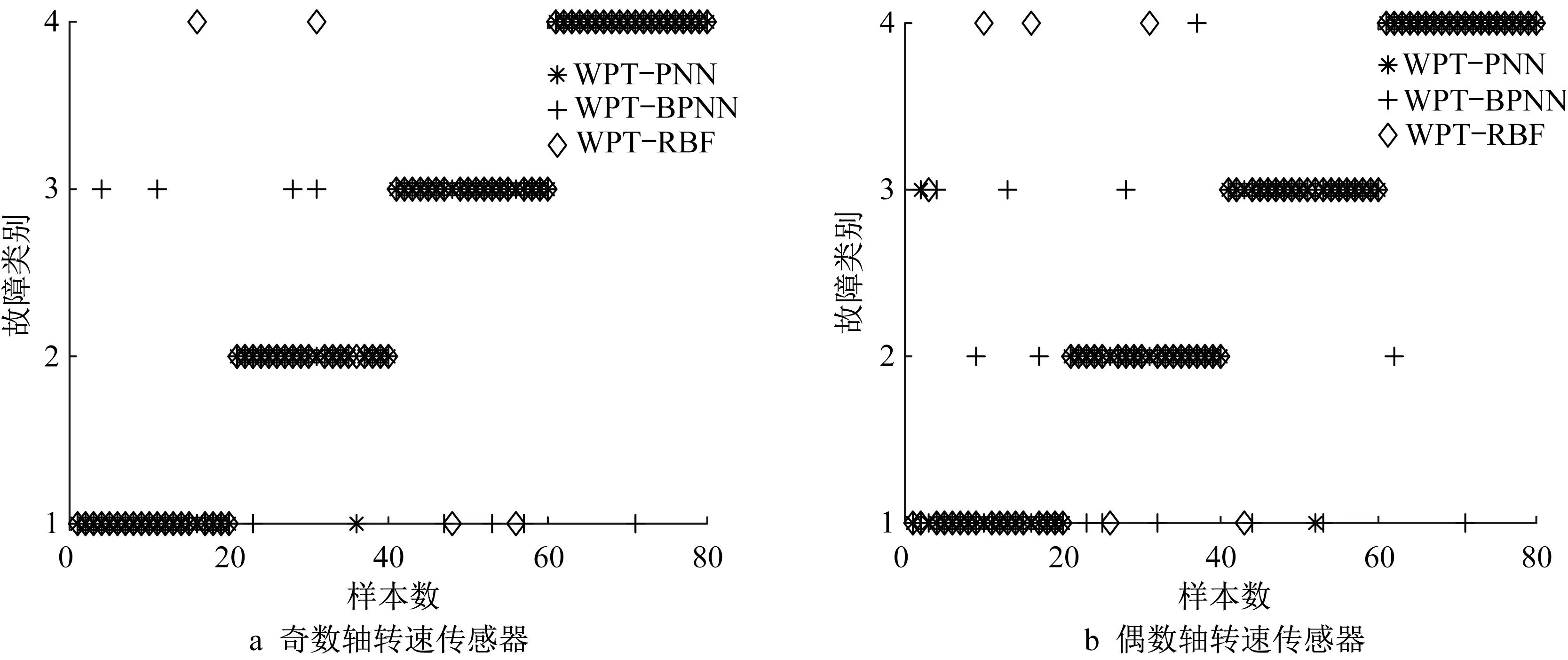
图10 转速传感器的诊断结果对比Fig.10 Comparison of diagnosis results for speed sensors
根据图10 统计每种类别的诊断结果,如表4 所示。结合图10 及表4 可以看出,WPT-PNN 对转速传感器的诊断仍保持了较高的正确率,相比WPTBPNN和WPT-RBF,WPT-PNN拥有较大优势,说明所采用的方法对于DCT 中的传感器具有良好的适用性。

表4 转速传感器的诊断结果对比Tab.4 Comparison of diagnosis results for speed sensors
3 结论
(1)采用数据驱动的方法对变速器传感器进行故障诊断,克服了基于模型以及基于规则的故障诊断方法的局限性,实现了对变速器传感器故障快速、准确的诊断。
(2)使用逐步回归算法建立变速器传感器模型,模型输出与实际传感器输出的差值作为WPTPNN的输入。从故障诊断与容错控制的角度出发,该模型还可在传感器故障时代替传感器,以最大限度地减小故障的影响。
(3)WPT-PNN 诊断正确率高,达到98.50%,使用性能稳定,诊断正确率不会随样本的变化而产生较大波动,诊断性能优于WPT-BPNN 和WPTRBF。另外,对2 个变速器输入轴转速传感器进行了故障诊断,正确率分别为98.75%和97.50%,证明了本方法对于变速器传感器的适用性。
作者贡献声明:
吴光强:指导论文方向,对论文的不足提出了建设性的意见。
陶义超:提出论文的研究思路,对论文的方法与验证部分进行了研究,撰写论文。
曾 翔:利用逐步回归算法建立了传感器模型。
