随机点锈蚀下圆形钢管轴压承载能力

2021-03-19赵中伟张宏伟

同济大学学报（自然科学版） 2021年2期

赵中伟，张宏伟，吴刚

（1.东南大学土木工程学院，江苏南京 211189；2.辽宁工程技术大学土木工程学院，辽宁阜新 123000）

圆形截面钢管目前已被广泛地应用于各种工业输送管道以及空间网格结构。对于钢结构而言，服役期间的锈蚀现象是不可避免的。锈蚀严重减小钢构件的有效厚度，降低构件的承载能力，从而引起局部的失稳鼓曲。我国在20 世纪七八十年代兴建了一大批钢结构，至今已有40余年的服役期。由于维护工作的不到位，这些结构都发生了不同程度的锈蚀。

锈蚀会严重降低钢构件的承载能力，同时锈蚀也是一个非常复杂的电化学过程。很多学者从微观角度对锈蚀的机理进行研究。Han 等［1］通过试验研究了G20Mn5QT 铸钢与Q345d 钢材对接连接的锈蚀现象。还有很多学者从宏观角度研究了锈蚀对钢筋混凝土［2-4］以及钢构件［5-6］力学性能的影响。徐善华等［7］对中性盐雾环境锈蚀H型钢柱的抗震性能进行了试验研究，基于试验数据建立了锈蚀H 型钢柱位移延性系数的退化模型以及累积滞回耗能与循环次数的关系。Ok等［8］对点锈蚀影响下的钢板进行了256次非线性有限元分析，研究了点锈蚀位置以及大小的影响，通过多元回归方法得到了局部锈蚀下平板极限承载能力的理论计算公式。郑山锁等［9-11］对锈蚀后钢结构以及钢筋混凝土的抗震性能进行了一系列的深入研究。

已有研究结果［12-14］表明，随着锈蚀程度的增加，钢材的剩余强度逐渐降低，但是目前并没有锈蚀钢管轴压承载能力降低程度与锈蚀程度之间的定量关系。钢管在大跨空间网格结构中有着广泛的应用并且以受轴力为主。随着我国一大批钢结构即将进入加固修复期，研究锈蚀钢管的轴压承载能力显得很有必要，因此重点研究了锈蚀参数，包括锈蚀深度、质量损失率、锈蚀坑大小以及钢材强度等级对锈蚀后钢管轴压承载能力的影响。

1 数值模型的建立

基于商业有限元软件Ansys建立了带有随机锈蚀缺陷的钢管有限元模型。随机有限元分析通常需要进行数万次的计算分析。采用Shell181单元建立钢管的数值模型，同时通过减小单元的厚度以模拟锈蚀缺陷的影响［15］。Shell181 单元尺寸设定为5 mm，该尺寸足以精确描述锈蚀坑的形状。实际工程中的锈蚀坑非常复杂，典型的锈蚀坑形状如图1 所示。图1中，Wc表示锈蚀坑的表面尺寸（即锈蚀坑表面的直径），Tc表示锈蚀深度。文献［16］中的计算结果表明，圆柱形的锈蚀坑对钢管承载能力的影响最为不利，同时也为了简化，本研究中将锈蚀坑的形状设定为圆柱形。文献［17］的研究结果表明，将锈蚀坑的形状设定为圆柱形是切实可行的。

图1 锈蚀坑的不同形状Fig.1 Shapes of corrosion pit

锈蚀的本质特征是随机性，首先就是位置的随机性，锈蚀坑的发生位置随机地分布在钢管的表面。利用随机函数来模拟锈蚀坑位置的随机性。为了简化，锈蚀坑在钢管表面每一个位置发生的概率相等，也就是锈蚀坑的位置服从均匀分布。在锈蚀坑发生的位置，壳单元的厚度被指定为t（1-Tc/t）。其中，Tc指锈蚀深度，t指钢管的初始厚度。

为便于施加轴向荷载，在钢管顶面的中心位置建立加载点，通过建立MPC184 刚性梁单元将钢管顶端节点与加载点相连接；同时，将钢管底面所有节点的平动自由度进行约束。带有随机初始缺陷的钢管数值模型如图2所示。图2中，F表示所施加的轴力，Ux、Uy和Uz表示钢管底部节点沿x、y和z轴的线位移。

2 数值模型的验证

2.1 试件设计

图2 随机点锈蚀钢管数值模型Fig.2 Numerical model of steel pipe with random pitting corrosion

为了验证所建立数值模型计算结果的可靠性，设计了5个带有人工点锈蚀的试件。试件统一采用外径和厚度分别为108 mm和4 mm的空心钢管。由于是研究钢管的轴压承载能力，因此将钢管的长度设计为150 mm，以减小初弯曲以及二阶效应对轴压承载能力的影响。构件的初弯曲以及二阶效应可以在整体结构中进行考虑［18-19］。采用人工钻孔的方式模拟锈蚀的影响。随机锈蚀的位置不易确定，因此采用简化的人工锈蚀，即锈蚀坑的位置预先指定。锈蚀孔的直径设定为15 mm。各试件的示意图以及编号如图3所示，试件的照片如图4所示。试件A-1并未进行钻孔，代表未锈蚀的构件。试验在200 t万能压力机上进行，以位移控制的形式进行加载，加载速度设定为0.5 mm·min-1。

2.2 试验结果对比分析

为了验证所建立数值模型的准确性，将试验所得荷载-位移曲线与数值模型所得结果进行对比。有限元所采用的钢材本构模型如图5a所示。该模型为由工程应力（σe）、应变（εe）按照式（1）和式（2）所转换的真实应力（σt）、应变（εt），如下所示：

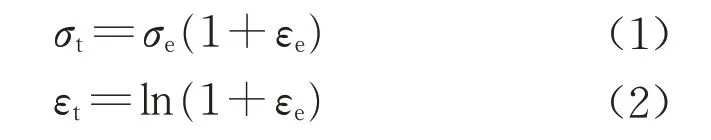
5个试验构件的荷载-位移曲线的对比结果如图5所示。从对比结果可以看出，采用Shell181单元所建立的带有锈蚀缺陷的数值模型可以准确模拟钢管的初始刚度、屈服荷载以及轴压承载能力。试件A-1所得结果的计算误差最大为8.6%，其他试件的结果吻合较好。试件A-1 属于强度破坏，误差来源为钢材本构的误差。该误差主要存在于强度退化阶段，并不影响本研究结论。试件的破坏模式如图6所示。从图6 可以看出，有限元模型中试件的破坏模式与试验结果一致。所建立的数值模型考虑了由于锈蚀所引起的应力集中效应，从而可以精确预测带有锈蚀缺陷钢管的轴压承载能力。

图3 试件示意图（单位：mm）Fig.3 Schematic diagram of test specimens（unit：mm）

图4 试件照片Fig.4 Photo of test specimens

3 轴压承载力的影响因素

为了更好地描述锈蚀对钢管轴压承载能力的影响，采用折减系数Rc来描述锈蚀后钢管轴压承载力的降低程度。折减系数Rc定义为锈蚀后钢管轴压承载力与锈蚀前钢管轴压承载力的比值，如下所示：

式中：Fu，c是锈蚀后钢管轴压承载力；Fu是锈蚀前钢管轴压承载力。

图5 试验结果Fig.5 Test results

采用折减系数的优点在于：当钢管的锈蚀参数确定以后，可以直接根据未锈蚀钢管的承载力Fu和折减系数Rc确定锈蚀钢管的极限承载力。在以下参数化分析中，钢材材料选用理想弹塑性本构模型。钢材的弹性模量E、屈服强度fy、切线模量Et分别为2.06×105MPa、235 MPa和0。

图6 破坏模式Fig.6 Failure mode

3.1 锈蚀深度对折减系数的影响

3.1.1 均匀锈蚀深度

在实际工程中，钢管不同位置的锈蚀深度Tc是随机分布的，为了简化，将Tc假定为常数，即钢管表面任意位置的锈蚀深度都是相同的，以揭示锈蚀深度对钢管轴压承载能力的影响。在本节计算中，锈蚀参数Wc的取值为10 mm。钢管的外径D、厚度t的取值分别为100 mm 和6 mm。所分析钢管的长度为300 mm。为了使所得结论具有普适性，使用量纲一参数Tc/t来代表锈蚀深度，将Tc/t分别假定为0.30、0.40、0.45、0.50、0.70和0.90。所得折减系数Rc随质量损失率χ的变化曲线如图7所示。图7中，黑实线代表均匀锈蚀时（即钢管厚度均匀减小），钢管轴压承载力折减系数的变化曲线。从图7可以看出，当Tc/t为常数时，钢管的最大质量损失率为Tc/t，此时钢管已由点锈蚀转变为均匀锈蚀，因此和图7中代表均匀锈蚀的直线相交。相交点的纵坐标即Rc值为（1-Tc/t），横坐标最大质量损失率为Tc/t。该结论与实际情况相符，进一步验证了计算结果的可靠性。

另外，从计算结果可以看出，点锈蚀所引起的折减系数在与均匀锈蚀对应的黑实线以下，说明点锈蚀不可以简单地简化为均匀锈蚀，否则所得折减系数Rc偏大，偏于不安全。

通过图8 可知，Rc-χ曲线与纵轴的交点代表未锈蚀钢管的折减系数，此时Rc的值为1，Rc-χ曲线的终点坐标为（Tc/t，1-Tc/t）。基于Rc-χ曲线的形状，将其数学方程假定为幂函数，根据终点坐标，则Rc的计算式如下所示：

图7 均匀锈蚀下Rc-χ曲线Fig.7 Curves of Rc- χ corresponding to uniform corrosion

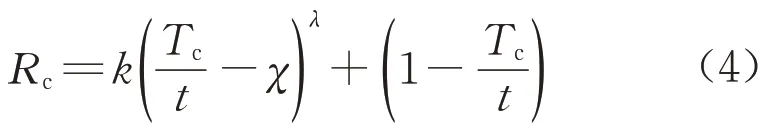
当χ为0 时，Rc为1，由此可进一步确定系数k的取值，计算式如下所示：

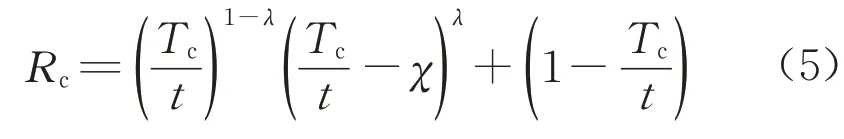
式（5）中只有一个待确定的指数λ。通过试算，将指数λ设定为5 时，结果吻合最好，结果对比如图8 所示。图8 中，黑实线代表理论计算结果。从结果对比可以看出，所提出的理论公式可以根据质量损失率χ精确预测均匀锈蚀厚度下钢管轴压承载力的折减系数，如下所示：

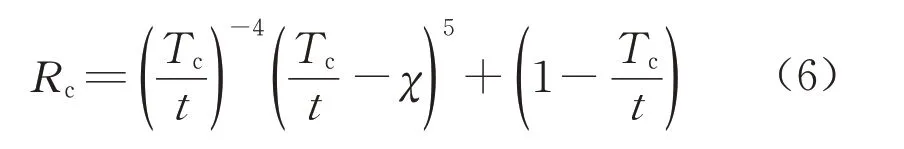
图8 理论结果与有限元结果对比Fig.8 Comparison between analytical and FE results

3.1.2 随机锈蚀深度

在实际工程中，不同位置的锈蚀深度是随机分布的，也就是说Tc/t是随机变量。为了研究Tc/t对Rc分布规律的影响，假定Tc/t服从（0～（Tc/t）max）的均匀分布，（Tc/t）max指最大锈蚀深度。锈蚀参数Wc和钢管几何参数与上节相同。将（0～（Tc/t）max）设定为（0～0.40）、（0～0.60）、（0～0.80）和（0～0.90）。由于Tc/t服从均匀分布，因此χ的最大值为（Tc/t）max/2。

随机锈蚀深度所对应的折减系数分布如图9所示。从图9 可以看出，随机锈蚀深度所对应的Rc分布与均匀锈蚀深度存在很大不同。当锈蚀深度服从（0～0.40）的均匀分布时，最小Rc为0.68，并不等于0.60，也不等于均匀锈蚀深度为（Tc/t）max/2 时的0.80。同样，锈蚀深度服从（0～0.60）、（0～0.80）和（0～0.90）时的最小Rc分别为0.55、0.41 和0.31。通过观察可以看出，随机锈蚀深度（0～（Tc/t）max）与均匀锈蚀深度3/4×（Tc/t）max等效，即当锈蚀深度服从（0～（Tc/t）max）的均匀分布时，可以将其简化成锈蚀深度为3/4×（Tc/t）max的均匀分布。此时，式（6）中的Tc/t需转化为其等效锈蚀深度3/4×（Tc/t）max，则式（6）仍可适用于随机锈蚀深度的计算。为了验证式（6）对于随机锈蚀深度下Rc计算的可靠性，将均匀锈蚀深度Tc/t等于0.300、0.450、0.600 和0.675时的Rc与随机锈蚀深度Tc/t所对应的Rc进行对比，如图9 所示。从计算结果可以看出，所提方法可以精确预测随机锈蚀深度下Rc的分布规律。

图9 随机锈蚀下Rc-χ曲线Fig.9 Curves of Rc- χ corresponding to random corrosion

3.2 点锈蚀大小对Rc的影响

在实际工程中，钢结构表面锈蚀坑的平面尺寸也是随机分布的，而上述分析中将锈蚀坑的表面尺寸简化为常数，即Wc=10 mm。为了研究这一简化对分析结果的影响，将Wc设定为10 mm、15 mm 和20 mm。锈蚀深度Tc/t分别设定为0.50和0.90。钢管的外径D、厚度t的取值以及所分析钢管的长度与前述分析相同。

基于不同Wc所得到的Rc随质量损失率χ的分布规律如图10所示。从计算结果可以看出，在锈蚀深度Tc/t相同的前提下，基于不同Wc所得到的Rc随χ的分布规律完全相同。也就是说，表面锈蚀坑的尺寸大小并不影响钢管轴压承载力折减系数的分布规律。这也说明前述分析基于Wc=10 mm 所得到的结论可以适用于随机Wc的实际情况。

图10 Wc对Rc-χ曲线的影响Fig.10 Effect of Wcon Rc-χ curves

3.3 钢材等级对Rc的影响

以上结论均是基于fy=235 MPa得到，而实际工程结构中会选用不同等级的钢材，因此为了研究本结论对于不同强度等级钢材的适用性，将钢材的屈服强度设定为235 MPa、345 MPa以及390 MPa。不同屈服强度下折减系数Rc随χ的变化规律如图11所示。从图11可以看出，不同屈服强度所对应的折减系数随χ的变化规律完全相同，因此所得结论可以适用于不同强度等级的钢材。

图11 fy对Rc-χ曲线的影响Fig.11 Effect of fyon Rc-χ curves

3.4 钢管厚度对Rc的影响

实际工程中所采用的钢管具有不同的半径或者厚度。为了研究所得结论对不同尺寸钢管的适用性，研究了钢管径厚比D/t对Rc-χ曲线的影响。在本节进行的分析中，钢管外径为100 mm，通过改变钢管壁厚来改变钢管径厚比D/t的大小。将钢管的厚度设置为1 mm、3 mm和6 mm。在钢管壁厚较薄或者钢材强度较高时可能会出现局部失稳的问题，因此将钢材强度设置为390 MPa。

不同径厚比所对应的Rc-χ分布曲线如图12 所示。从图12 可以看出，钢管壁厚为1 mm 时所对应的Rc要小于壁厚为3 mm 和6 mm，当Tc/t的取值为0.90 时，这一现象更为明显。原因是当钢管壁厚太薄时（壁厚小于1 mm），会出现局部失稳的现象，从而降低了钢管的承载能力。这可以从如图13 所示的失效模式得到。局部失稳使钢管的失效由强度问题转化为稳定问题，使钢管在材料强度完全发挥出来之前失效，进而降低了Rc。当t和Tc/t的取值分别为1 mm 和0.90，质量损失率增加到0.90 时，钢管壁厚的有效值为0.1 mm，D/t的值为1 000，这种大径厚比的钢管不会应用于实际结构，尤其是空间网格结构。当t和Tc/t的取值分别为6 mm和0.90时，钢管壁厚的有效值为0.6 mm，此时D/t的值为167。从图12a 可以看出，当D/t的值为167 时，所得结论完全适用。因此，本研究结论只适用于径厚比小于167的轴压锈蚀钢管。

图12 D/t对Rc-χ曲线的影响Fig.12 Effect of D/t on Rc-χ curves

我国空间网格结构技术规程规定，杆件截面的最小尺寸应根据跨度和网格大小确定，网架和双层网壳空心球的外径与壁厚之比宜取25～45，单层网壳空心球的外径与壁厚之比宜取2.0～3.5，空心球外径与主钢管外径之比宜取2.4～3.0，空心球壁厚与主钢管的壁厚之比宜取1.5～2.0。因此，实际空间网格结构工程中所采用的钢管径厚比通常为12.5～37.5，该值远小于167。对于承受轴心拉力的锈蚀钢管，由于不存在局部稳定问题，因此本研究结论也是完全适用的。