局部织构无限长可倾瓦推力轴承 流体动压润滑分析

纪敬虎，邓智文，陈天阳，房鲁南，符永宏

（江苏大学，江苏 镇江 212013）

流体动压润滑的推力轴承广泛应用于水轮机、泵和船舶推进器等重型机械设备，是重要的基础零部件[1]。推力轴承表面的流体动压润滑性能和承载能力，对机械设备的工作性能、使用寿命和可靠性具有决定性的作用[2]。可改善推力轴承的润滑性能，在推力瓦表面制备具有一定分布规律和相应尺寸的微结构，推力轴承的润滑性能是当前表面工程和摩擦学领域的热点课题之一[3-4]。

通过对推力轴承入口区进行粗糙化处理，可以在表面形成有效的收敛楔形间隙，从而使油膜产生承载能力[5]。受此启发，人们提出利用局部表面织构平面推力轴承来提高承载能力，即在入口区制备规则微凹坑织构，利用局部织构化区域微凹坑的“富集效应”来实现，其作用类似于传统斜面滑块和阶梯滑块[6-7]。随着研究的深入，发现斜面滑块表面的入口区经局部织构处理后，可以增强流体动压润滑效应，减小摩擦[8]。因此，局部织构被引入到可倾瓦推力轴承中[9-11]，并基于流体动压润滑理论发展了局部织构的“平衡楔效应”。即利用局部织构增强表面的楔形收敛效应，一方面提高油膜承载能力，另一方面通过改变油膜压力分布，提高可倾瓦推力轴承的平衡性能。目前，针对局部织构可倾瓦推力轴承的理论研究都是采用一维理论模型，虽然能在一定程度上反映表面织构对油膜压力的影响，但是由于表面织构形貌的多样性及其分布规律的复杂性，一维润滑理论模型具有较大的局限性。

本文将在上述研究的基础上，建立二维局部凹坑织构无限长可倾瓦推力轴承润滑理论模型，利用数值分析的方法研究凹坑织构对流体动力润滑性能的影响。

1 理论模型

1.1 几何模型

本文忽略曲率半径的影响，假设扇形可倾瓦的径向宽度远大于周向宽度，则可认为扇形可倾瓦在垂直于运动方向上无限长，其几何结构如图1 所示。上表面为宽度bx的局部微凹坑织构可倾瓦，可绕中心枢轴点xp旋转，下表面为光滑滑块，相对上表面以速度U 滑动。凹坑横截面为抛物线，半径为rd，深度为hd。入口处油膜厚度为h1，出口处油膜厚度为h0，定义收敛比为K，则K=(h1-h0)/h0。

图1 局部凹坑织构化无限长可倾瓦推力轴承结构示意图 Fig.1 Partially dimple textured infinitely long tilting pad thrust bearing

图2 为局部凹坑织构化可倾瓦表面结构示意图，凹坑织构规则地分布于可倾瓦表面，水平间距和纵向间距分别为sx、sy。织构区域宽度为bt，入口处到织构区域的距离为si。局部织构比定义为γt，代表织构区域宽度与可倾瓦宽度之比，即γt=bt/bx。描述局部织构位置参数定义为局部织构位置比γt，代表入口处到织构区域的距离与无织构宽度之比，γt=si/(bx-bt)。

图2 局部凹坑织构化可倾瓦表面结构示意图 Fig.2 Partially dimple textured tilting pad surface

假定轴瓦在纵向上无限长，因此可以忽略纵向的边界效应。此外，织构周期性分布于轴瓦表面，其周期长度为cy，并且cy=2rd+sy。因此，为了减少计算量，在水平方向上取一单行凹坑织构作为计算单元，建立直角坐标系如图3 所示。

图3 单行凹坑织构计算单元及其笛卡尔坐标系 Fig.3 Single-row dimple texture calculation unit and its Cartesian coordinate system

1.2 数学模型

假设润滑油充满摩擦表面接触区域，润滑状态为流体动压润滑。对于不可压缩牛顿流体，在稳态层流条件下，油膜压力控制方程如下:

式中：p 为油膜压力，h 为油膜厚度，ρ 为润滑油密度。

基于质量守恒的JFO 空化边界条件，采用Elrod空化算法[12]，引入通用变量θ（θ=ρ/ρc）和开关函数g，则压力控制方程转变为：

式中：β 为润滑油体积模量，β=ρ∂p/∂ρ；开关函数g 由（3）表示。

式中，pc为润滑油膜空化压力。

润滑油膜厚度方程为：

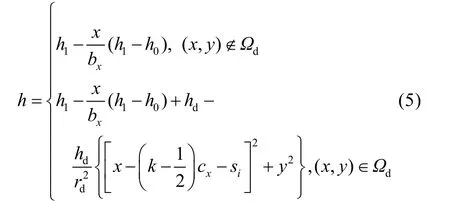
式中：cx=2rd+sx；k=1, 2, 3,···, nd，其中nd为凹坑数目；Ωd为凹坑区域。

为了提高数值稳定性，定义无量纲参数如下：

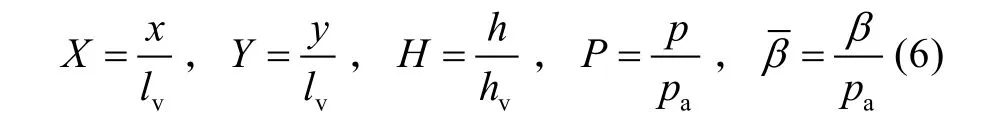
式中：lv为x 和y 的无量纲参考量，hv为h 的无量纲参考量，pa为大气压力。

式中：H0=h0/hv，H1=h0/hv，Bx=bx/lv，Hd=hd/hv，Rd=rd/lv，Cx=cx/lv，Si=si/lv。

无量纲油膜压力的计算公式如下：

无量纲油膜压力边界条件如下：

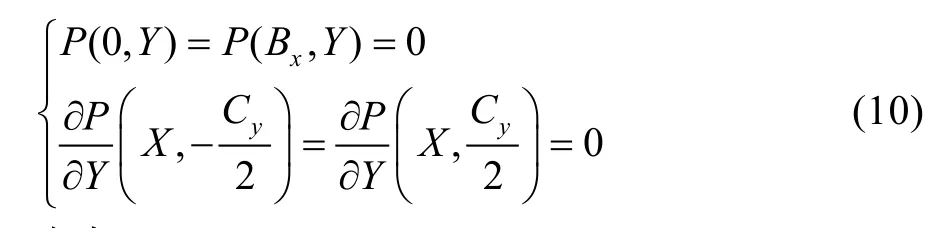
式中：Cy=cy/lv。

单行凹坑织构计算单元内无量纲油膜承载力计算公式如下：

式中：Ω 为单行凹坑织构计算区域。

本文以油膜平均无量纲压力作为局部凹坑织构化可倾瓦推力轴承的评价指标，其计算公式为：

式中：Au为计算单元的无量纲面积，Au=BxCy。

俄罗斯实行独家垄断型管理模式，上中下游业务一体化运营，受前苏联计划经济的影响，俄天然气管网始终由政府统一管理，国家干预性极强。俄罗斯天然气管道系统全部归俄罗斯天然气工业股份公司（Gazprom）下的俄罗斯天然气运输股份公司垄断经营。俄罗斯天然气工业股份公司是苏联解体后在原苏联天然气工业部的基础上建立起来的，主要从事天然气勘探、开发、生产、加工、储运以及销售，是一家上中下游业务一体化的国有垄断性公司，也是世界上最大的天然气公司。俄罗斯国内天然气消费量的近70%由俄罗斯天然气工业股份公司供应。

1.3 数值求解方法

为了便于进行数值计算，无量纲雷诺方程可以表示如下[13]：

与有限差分法和有限元法相比，多重网格法是一种快速有效的求解稠密网格非线性问题的方法[14]。在本文中，使用多重网格法处理式（12），其流程如图4 表示。两个相邻层间的网格结构如图5 所示。

图4 m=3 时的V 循环流程图 Fig.4 V cycle flow chart when m=3

图5 二维问题的网格结构 Fig.5 Grid structure of a two-dimensional problem

式中：kv是V 循环次数。整个计算过程如图6所示。

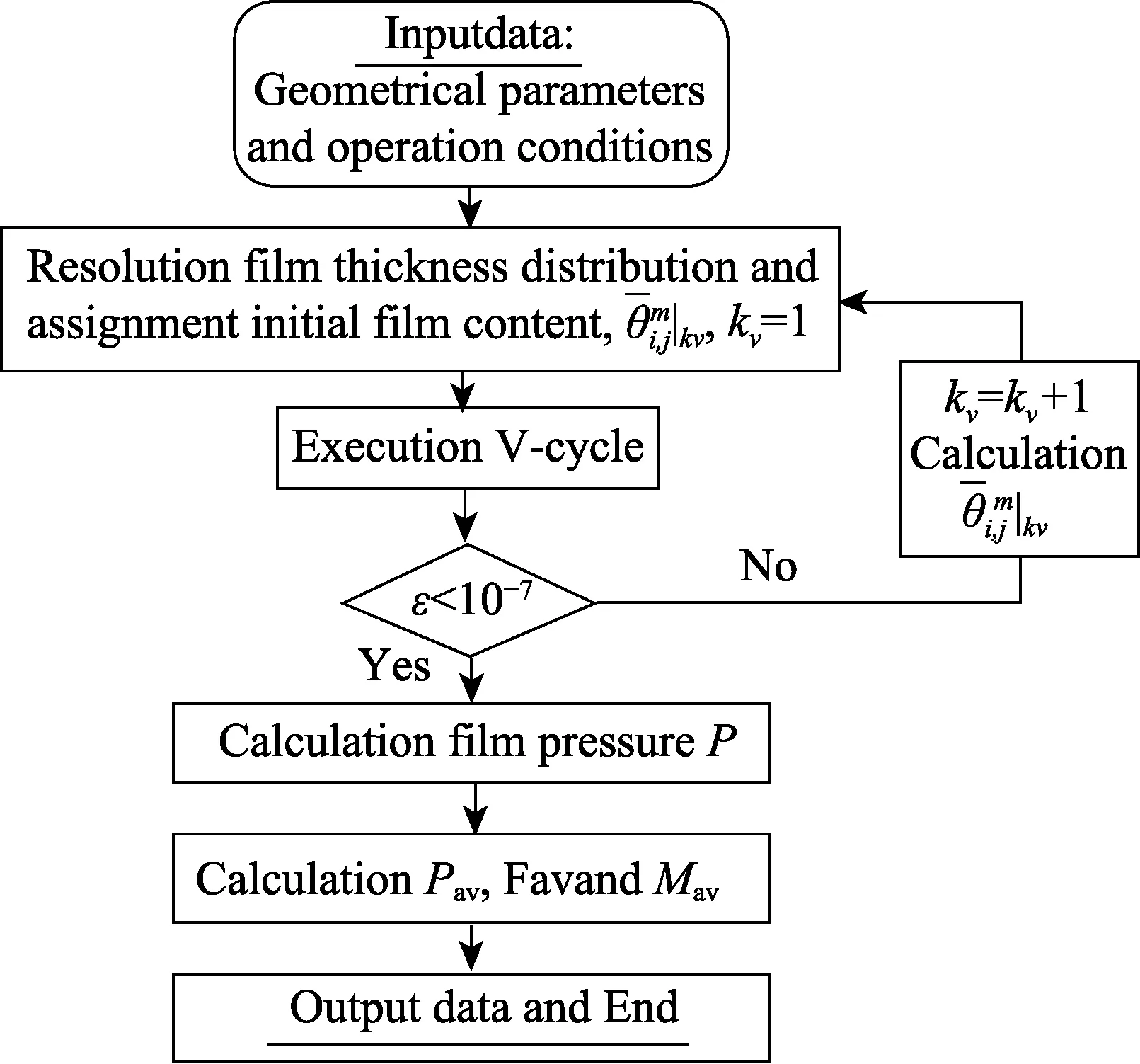
图6 整个计算过程的流程图 Fig.6 Flow chart of the entire calculation process

2 模型验证及结果分析

2.1 模型验证

模型的几何参数和工作条件如表1 所示。计算过程中使用均匀网格，最密集的网格的步长为ΔX=0.25和ΔY=0.25。

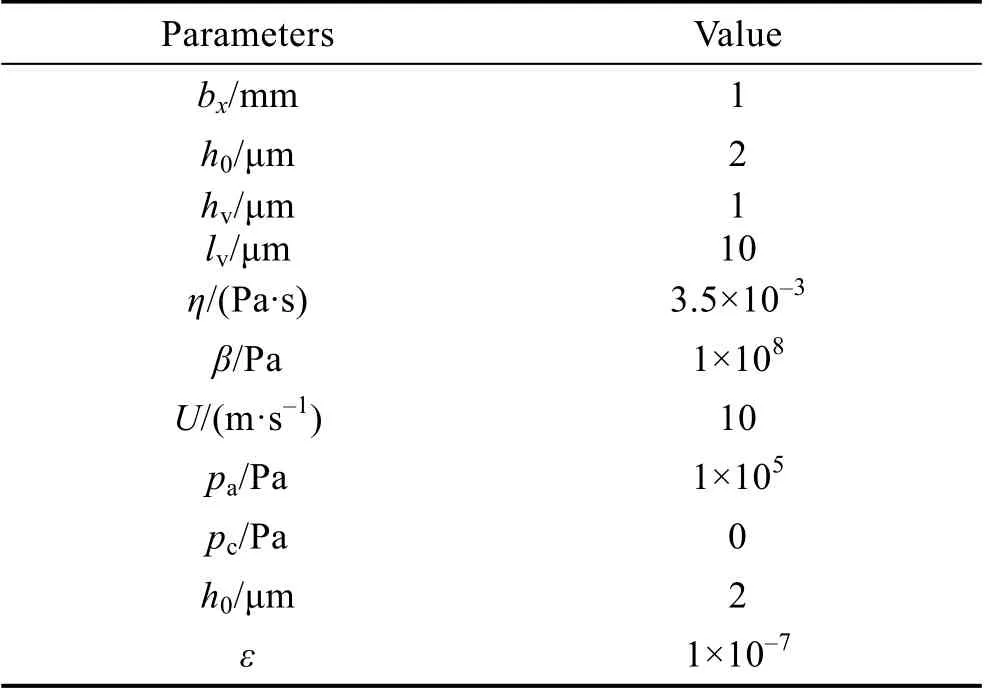
表1 模型几何参数和工作参数 Tab.1 Geometrical parameters and operating conditions

为了验证模型准确性，将对比分析未织构无限长可倾瓦推力轴承流体动压润滑解析解与数值解的结果。对于未织构无限长可倾瓦推力轴承，在流体润滑问题的计算中，可以将其简化为求解一维问题，润滑油膜压力的解析解表达式为[26]:

在此，比较了无限长可倾瓦推力轴承流体动压润滑的解析解和数值解。图7a 为无量纲油膜平均压力的解析解和数值解随收敛比的变化曲线。可以看出，油膜平均压力的解析解与数值解与收敛比的变化规律相同，存在相同的最佳收敛比K=1.2，此时油膜平均压力达到最大，二者之间的偏差约为4.35%。在最佳收敛比附近，数值解和解析解的结果存在一定的偏差；而在其他区域，数值解与解析解的偏差非常微小。图7b 为解析解和数值解的无量纲油膜压力分布曲线，可以看出，解析解和数值解的油膜压力分布规律相同，且都在X=68.75 处达到峰值。解析解和数值解的油膜压力在峰值附近存在一定的偏差，而在其他区域偏差较小，二者之间的最大偏差约为6.43%。

基于上述分析，利用本文所建立的理论模型和数值求解方法获得润滑油膜流体动压润滑效应与解析基本一致，偏差较小，从而证明了所建立的理论模型和数值求解方法的有效性。

图7 无限长可倾瓦推力轴承流体动压润滑解析解与数值解结果 Fig.7 Analytical solution and numerical solution of hydrodynamic lubrication of infinitely long tilting pad thrust bearing (a) the average pressure curve based on convergence ratio and (b) the pressure distribution of oil film at K=1.2

2.2 结果分析

2.2.1 油膜压力分布

图8、图9 和图10 分别给出了收敛比K=0.2 时，未织构、局部凹坑织构和全部凹坑织构无限长可倾瓦推力轴承表面润滑油膜厚度和压力分布。图8 为未织构表面的润滑油膜压力分布。可以看出，在沿运动方向，两表面形成了收敛楔形间隙，产生了流体动压润滑效应，油膜压力先增大后减小，约在X=55 出现峰值；在垂直于运动方向，由于膜厚没有变化，因此油膜压力也没有变化。图9 为局部凹坑织构表面的润滑油膜压力分布。可以看出，在沿运动方向，由于在入口区设置的微凹坑织构，增大了两表面所形成的收敛楔形间隙，此时微凹坑的“富集效应”增强了油膜的流体动压润滑效应；此外，在入口区油膜压力呈阶梯状递增，油膜压力峰值出现在局部织构区末端。图10 为全部凹坑织构表面的润滑油膜压力分布。可以看出，在沿运动方向，润滑油膜压力呈折叠状先增加后减小，约在X=60 出现峰值。由于在出口区设置了凹坑，一方面削弱了微凹坑的“富集效应”，另一方面，增大的出口区的油膜厚度使收敛比降低，从而抑制了流体动压润滑效应的产生。

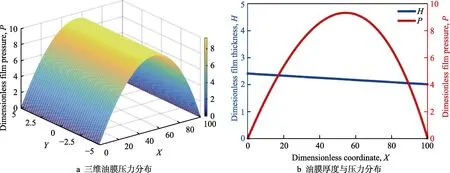
图8 未织构无限长可倾瓦推力轴承表面流体动压润滑效应 Fig.8 Hydrodynamic lubrication effect on the surface of non-textured infinitely long tilting pad thrust bearing: a) 3D film pressure distribution; b) film thickness and pressure distribution

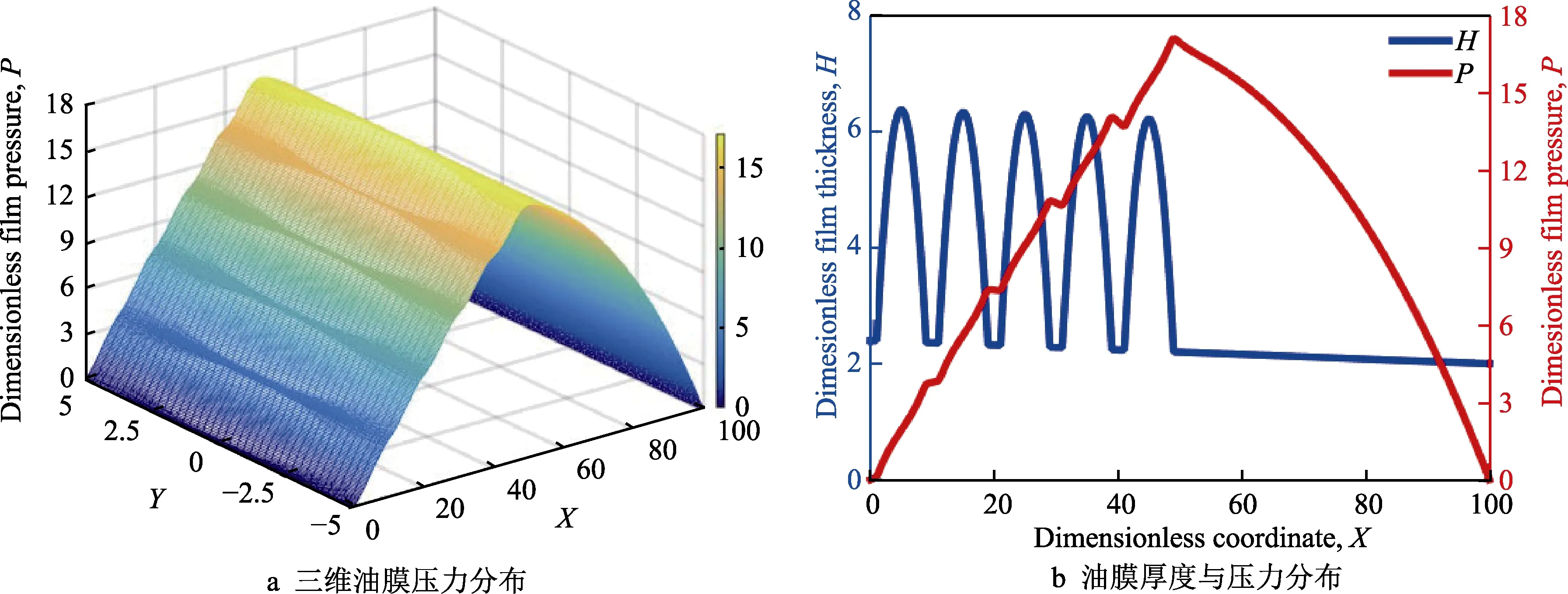
图9 局部凹坑织构无限长可倾瓦推力轴承表面流体动压润滑效应 Fig.9 Hydrodynamic lubrication effect on the surface of partially dimple textured infinitely long tilting pad thrust bearing: a) 3D film pressure distribution; b) film thickness and pressure distribution

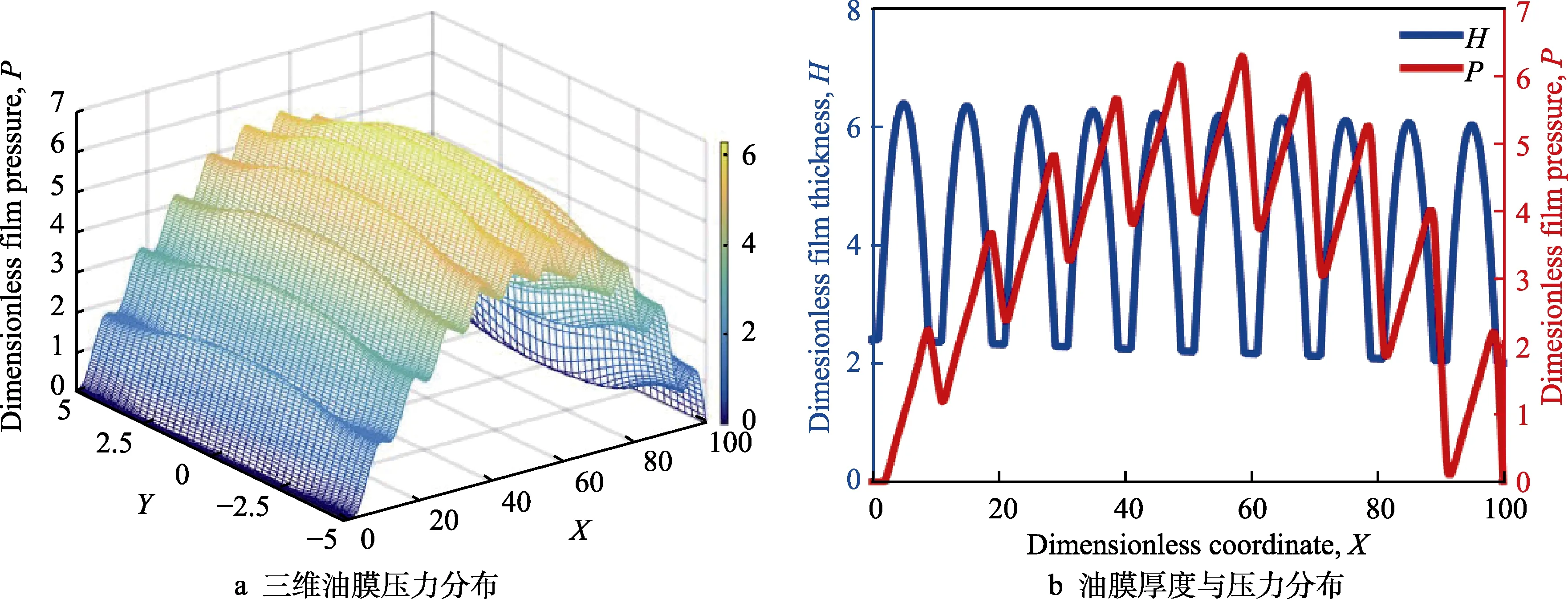
图10 全部凹坑织构无限长可倾瓦推力轴承表面流体动压润滑效应 Fig.10 Hydrodynamic lubrication effect on the surface of totally dimple textured infinitely long tilting pad thrust bearing: a) 3D film pressure distribution; b) film thickness and pressure distribution

2.2.2 不同收敛比下局部织构比对承载能力的影响

图11 给出了不同收敛比下油膜无量纲平均压力随局部织构比的变化曲线。可以看出，局部织构比对油膜承载能力有较大的影响。当收敛比较小时，油膜承载能力随局部织构比增加而先升高后降低，最优局部织构比约为0.6。这主要是因为当收敛比较小时，局部凹坑织构能够起到增大收敛楔形间隙和产生凹坑“富集效应”的作用，从而增强流体动压润滑效应。随着收敛比的增大，局部凹坑织构对承载能力的影响变小，这主要是因为随着收敛比的增大，局部凹坑织构对收敛楔形间隙的影响逐渐减弱。

图11 不同收敛比下油膜平均压力随局部织构比的变化曲线 Fig.11 The effect of the textured extent on dimensionless average pressure at various convergences

2.2.3 不同局部织构比下局部织构位置比对承载能力的影响

图12 给出了不同局部织构比下油膜无量纲平均压力随局部织构位置比的变化曲线。由图可以看出，油膜承载能力随着局部织构位置比的增大而逐渐减小。这主要是因为随着局部织构位置比的增大，入口区的平均油膜厚度减小，降低了收敛楔形间隙，使得 收敛比也随之减小，从而削弱了流体动压润滑效应，降低了油膜承载能力。

图12 不同局部织构比下油膜平均压力随局部织构位置比的变化曲线 Fig.12 The effect of the textured location extent on the dimensionless average pressure at various textured extents

2.2.4 不同收敛比下凹坑深度对承载能力的影响

图13 给出了不同收敛比下油膜无量纲平均压力随凹坑深度的变化曲线。由图可以看出，当K≤1.2时，油膜承载能力随着凹坑深度的增加，呈先增大后减小的趋势，存在最佳凹坑深度使得油膜承载能力达到最大，且最佳凹坑深度随着收敛比的增加而减小。这主要是因为随着凹坑深度的增大，入口区的油膜平均厚度增大，从而提高了收敛楔形间隙，油膜承载能力也随之增大。然而，当凹坑深度继续增大时，微凹坑内所形成的发散楔形间隙也随之增大，从而抑制了流体动压润滑效应。

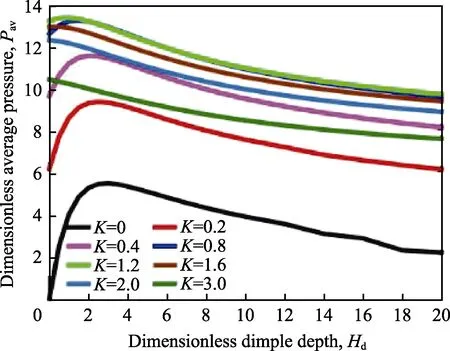
图13 不同收敛比下油膜平均压力随凹坑深度的变化曲线 Fig.13 The effect of the dimensionless dimple depth on the dimensionless average pressure at various convergences

2.2.5 不同收敛比下凹坑纵向间距对承载能力的影响

图14 为不同收敛比下油膜无量纲平均压力随凹坑纵向间距的变化曲线。可以看出，当收敛比较小时，油膜承载能力随着凹坑纵向间距的增大而减小。这主要是因为凹坑面积密度随着纵向间距的增大而减少， 入口区的平均油膜厚度也随之减小，从而使得收敛比降低。随着收敛比的增大，凹坑对入口区平均油膜厚度的影响也随之减弱，因此对油膜承载能力的影响也越来越小。

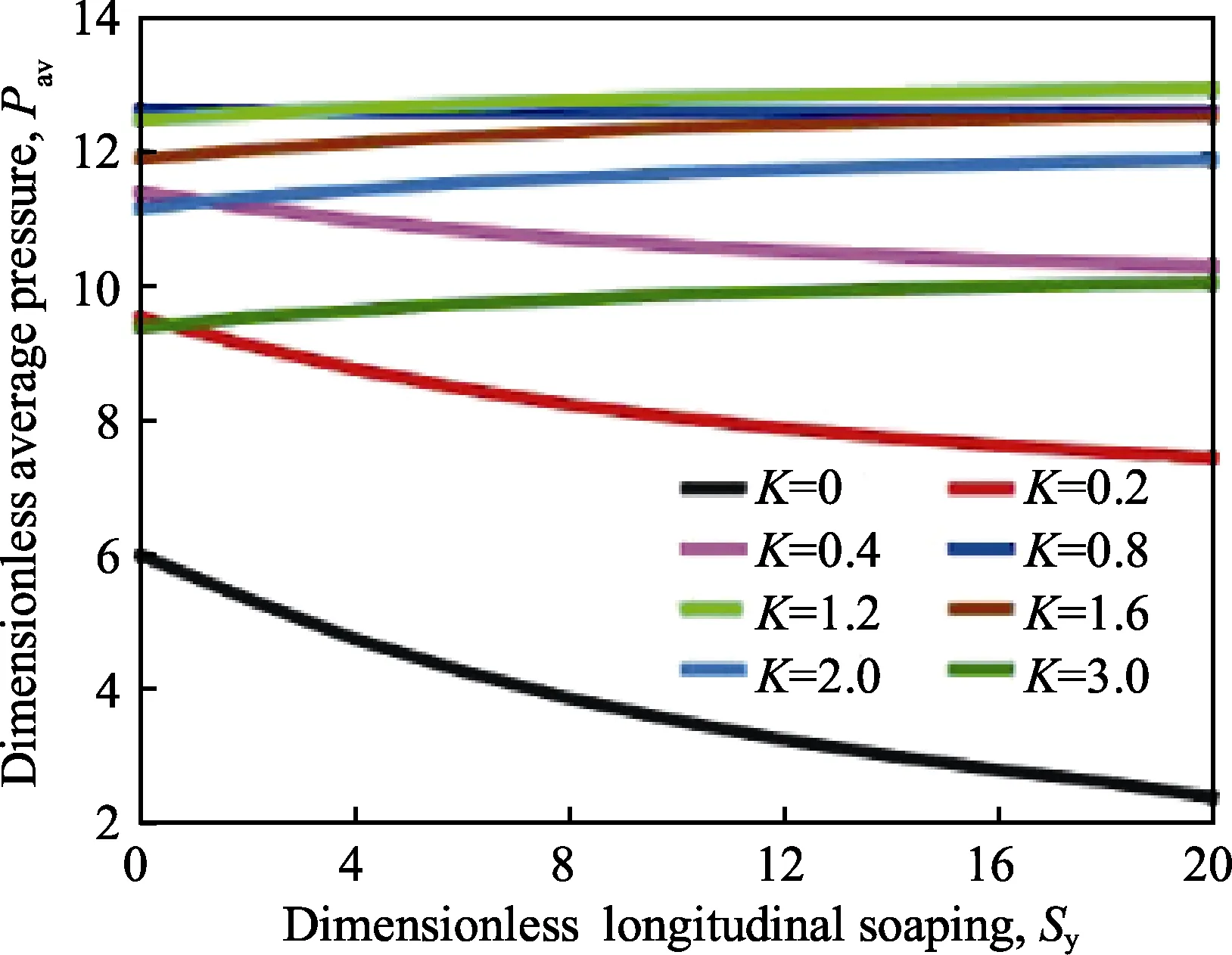
图14 不同收敛比下油膜平均压力随凹坑纵向间距的变化曲线 Fig.14 The effect of the dimensionless longitudinal spacing on the dimensionless average pressure at various convergences

2.2.6 不同收敛比下凹坑数目对承载能力的影响

图15 为不同收敛比下油膜无量纲平均压力随凹坑数目的变化曲线。可以看出，当收敛比较小时，油膜承载能力随着凹坑数目的增大而增大。这主要是因为随着凹坑数目的增大，入口区的平均油膜厚度也增大，从而增加了收敛比，提高了油膜流体动压润滑效应。随着收敛比的增大，凹坑数目对入口区平均油膜厚度的影响也减弱，因此对油膜承载能力的影响也越来越小。

图15 不同收敛比下织构数量对无量纲平均油膜压力的影响 Fig.15 The effect of number of dimples on the dimensionless average pressure at various convergences

3 结论

1）本文所建立的二维局部织构无限长可倾瓦推力轴承理论模型的数值解与解析解误差较小，能够有效地分析油膜流体动压润滑性能。

2）当收敛比较小时，在入口区进行局部微凹坑织构化处理能增强流体动压润滑效应，并存在最优局部织构比使得油膜承载能力达到最大；而当收敛比较大时，局部微凹坑织构对油膜承载能力的影响较小。

3）油膜承载能力随着局部织构位置比的增大而逐渐减小。存在最优凹坑深度，能够最大化轴承的承载能力，并且最佳凹坑深度随着收敛比的增加而减小。

4）油膜承载能力随着凹坑纵向间距的增大而减小，随着凹坑数目的增大而增大。