基于稳健回归的激光视觉异常值识别
2021-03-19要志斌马立峰智晋宁蔺素宏
要志斌,马立峰,智晋宁,蔺素宏,程 鹏
(1.太原科技大学 a.重型机械教育部工程研究中心,b.机械工程学院,太原 030024;2.太原理工大学 物理与光电工程学院,太原 030024)
在冶金工业和金属加工行业中棒材的轮廓尺寸是非常重要的测量内容。棒材轮廓的测量一般采用指示量具进行机械测量,或者采用圆度仪和坐标测量机进行测量[1-3]。基于机器视觉的激光测量法逐渐成为轮廓参数测量的新手段,相对于传统测量方法,可实现实时在线测量,具有测量精度高,速度快,无损伤的特点[4-6]。对于实现加工装备的信息化和智能化具有重要意义。
本文采用基于线结构光的激光视觉系统对棒材轮廓进行了测量研究。在测量过程不可避免的存在异常值,当数据被异常值污染,会造成模型参数的错误估计,得到错误的分析结果[7],所以必须采取措施,识别和剔除异常值。受到数据分布形态、数据量大小以及自身算法的限制,常用的异常值识别法在激光轮廓测量中存在稳健性差、应用困难的问题。
本研究提出一种基于稳健局部加权回归的异常值识别法来实现轮廓孤立异常值的有效识别。该算法利用稳健局部加权回归,即综合局部多项式估计与局部加权回归的稳健拟合法开展数据平滑,再计算平滑数据与测量数据的残差值,最终依据3σ准则判别出轮廓异常值。本研究依据该算法对棒材激光轮廓数据进行异常值识别,并开展轮廓椭圆的拟合分析,以验证该方法在激光轮廓检测中的有效性。
1 基于激光视觉的轮廓测试系统
激光视觉测试系统的工作原理如图1所示,该系统主要由激光视觉传感器、运动控制平台以及工业计算机组成,可对棒材外廓尺寸进行精确测量。激光视觉传感器采用线结构光扫描方式,即激光光源向空间投射出一平面光,此平面光在被测工件表面形成调制光带,再利用相机镜头与像平面的透视几何关系,获取高精度数字图像,根据激光三角测量原理,计算得到截面轮廓数据。利用运动控制系统沿轴向测量棒材轮廓,则可得到被测工件各截面轮廓云点数据[8-10]。
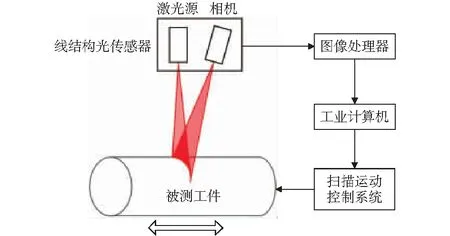
图1 激光视觉测试系统组成及工作原理
所获轮廓云点数据如图2所示。由图可见,轮廓中部存在明显异常值,该类异常值常以单点或双点的形式孤立出现,与其前后数据质量无必然联系,故该类异常值被称为孤立型异常值,或孤立野值[11-12]。这些异常值的出现极大影响了测量的精度和准确度,并导致错误的测量结果,所以必须对其加以识别和剔除。
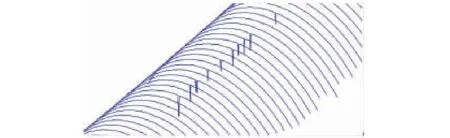
图2 所测扫描轮廓
2 基于稳健局部加权回归的异常值识别法
稳健局部加权回归(robust locally weighted regression,RLWR)属于非参数估计方法。非参数估计是现代统计分析的重要研究方向,其不依赖于样本所属总体的分布形式,无需对总体分布参数进行估计,仅从样本数据就可获取所需的信息,得到样本序列的分布结构,相对于参数估计,其适用范围更为广泛,对减小偏差、提高预测精度、了解样本动态结构都具有重要意义[13]。稳健局部加权回归由局部加权回归(locally weighted regression,LWR)发展而来,是一种综合局部多项式估计和局部加权回归的稳健拟合过程。该方法最早由CLEVELAND提出[14-15],并由CLEVELAND和DEVELIN进一步完善[16],因其稳健的非参数回归特性,逐渐得到重视,应用于科学研究的不同领域[17-18]。
本研究基于稳健局部加权回归方法,结合3σ准则实现对激光轮廓异常值的有效识别,可称为基于稳健局部加权回归的莱特识别法,其基本思路为依次提取一定比例的局部数据,在该子集中拟合多项式加权回归曲线,利用最小二乘法估计数据的局部规律和趋势,随着提取范围的推进,得到连续平滑的拟合曲线,计算平滑数据与原数据的残差,再利用3σ准则判别出异常值,其具体算法如下:
设所测数据序列为{xi,yi},i=1,2,…,n,其数据模型关系如下:
yi=g(xi)+εi.
(1)
式中:g为多项式平滑函数,εi为均值为0的独立分布的随机变量。
设,局部加权回归的权函数为w(x),权函数w(x)一般选取3次权重函数,如式(2)所示:
(2)
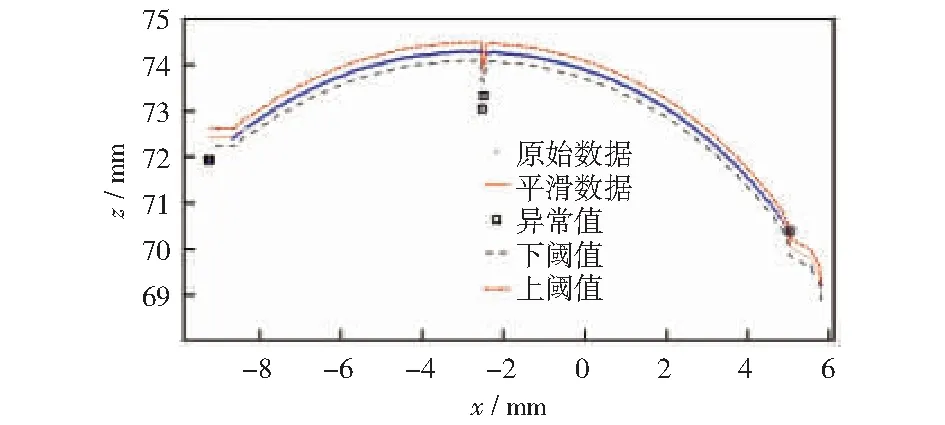
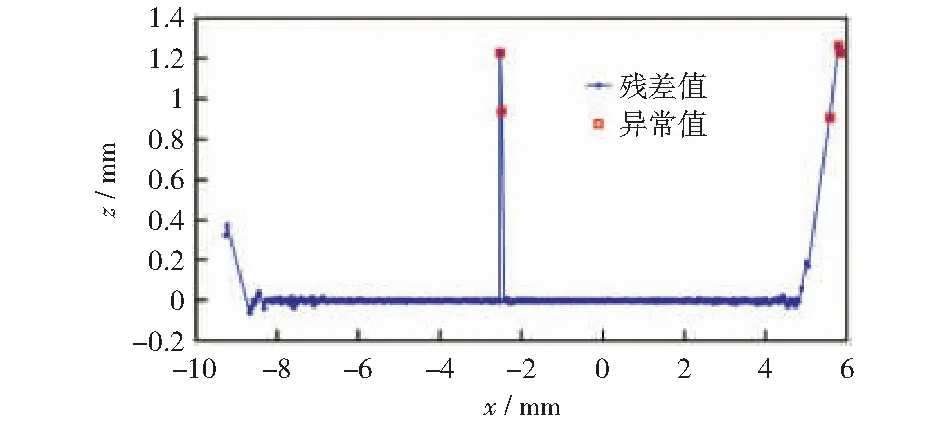
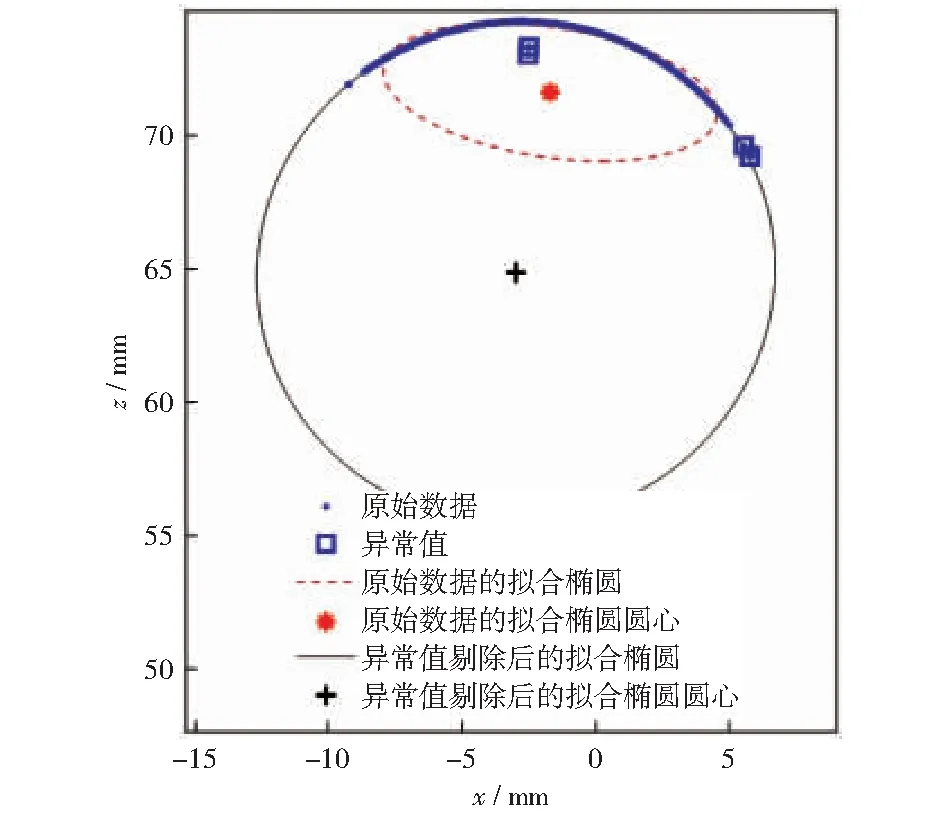
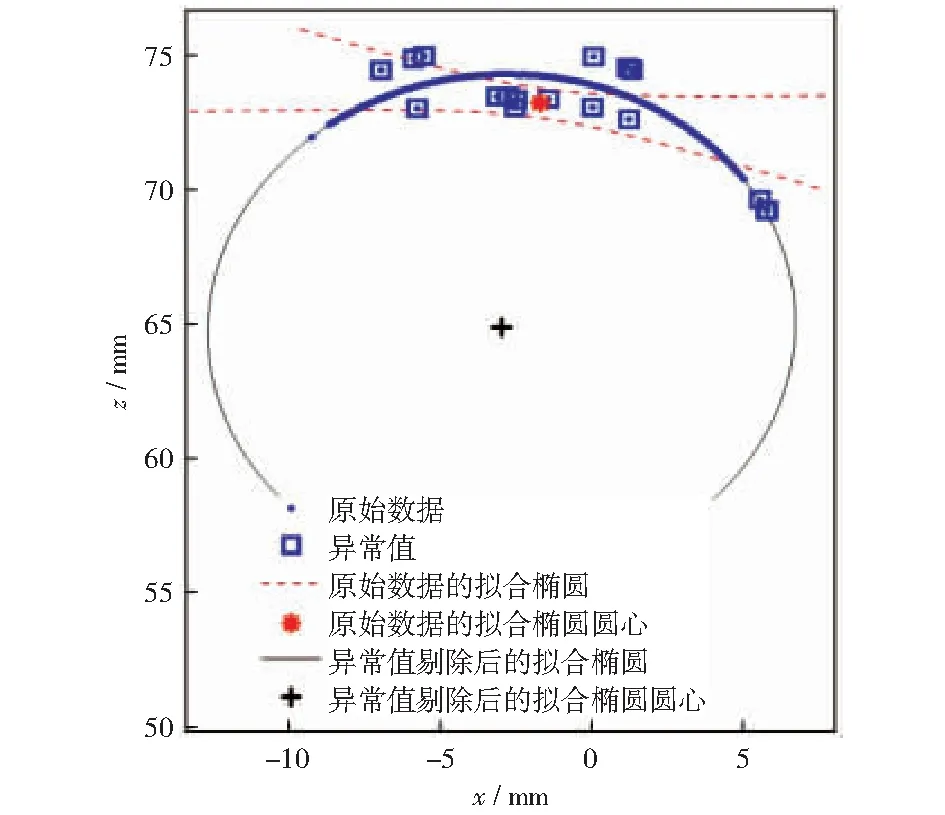
设,平滑系数为f,且0 首先以各观测点xi为中心,选取适当的f,确定其移动窗宽为xi±r. 再根据所选权函数w(x),以xi为中心,为窗内各数据得到对应的权重w(xi),如式(3)所示: (3) (4) 此时,设定稳健局部加权回归的4次鲁棒权重函数Q(zi),如式(5)所示: (5) (6) 重复上述鲁棒增强步骤,经过多次迭代,最终得到的稳健局部加权拟合值。 (7) 当所测数据残差与其均值之差大于3倍标准差时,即认为是异常值,如式(8)所示: (8) 针对典型轮廓数据,采取不同的移动窗宽,分别运用移动均值识别法和基于稳健局部加权回归的异常值识别法开展孤立异常值的识别和分析。 3.1.1移动均值法识别异常值 移动均值法是较为经典的异常值识别法,其基本思路为依次提取指定窗宽内的局部数据,计算其局部均值和局部标准差,再利用3σ准则判断异常值。实验中,移动窗宽从5逐步增加,观察其识别效果。如图3所示,窗宽增加到17时,才识别出数据中部的单个孤立异常点;当窗宽扩展到28时,才能正确识别出数据中部的双点孤立异常值,如图4所示。图中圆点数据为所获轮廓数据,方框为识别出的异常值。 图3 当窗宽为17时移动均值法识别出的异常值 图4 当窗宽为28时移动均值法识别出的异常值 由图3,4可见,异常值的存在,使得局部均值大幅度提高,异常值所处位置的判别阈值出现大幅度的增加。随着窗宽增加,中部阈值曲线逐渐平滑,上、下阈值范围逐渐减小,轮廓中部异常值识别能力有所提高;然而随着窗宽的增加,轮廓两侧的上、下阈值范围却明显增加,表明轮廓两侧的异常值识别能力会随窗宽的增加而下降。 3.1.2稳健局部加权回归法识别异常值 利用基于稳健局部加权回归的异常值识别法对该轮廓进行识别。选取不同的移动窗宽观察轮廓的平滑效果以及异常值识别情况。当窗宽为5时,如图5所示,该方法已能识别出轮廓中部的双点孤立异常值,但受异常值影响,其平滑曲线及其上下判别阈值随之波动,并将轮廓两端部分间断点识别为异常值。 图5 当窗宽为5时RLWR法识别异常值 逐步增加窗宽,当窗宽为9时,如图6所示,所拟合曲线和上下阈值曲线更为平滑,仅在轮廓两端,曲线出现轻微偏移。 图6 当窗宽为9时RLWR法识别异常值 图7为原始数据与平滑数据的残差值,利用3σ准则识别出孤立异常值,以及轮廓右端异常数据。轮廓端部异常数据的产生的原因主要是激光在圆弧边缘存在边缘效应,产生异常间断数据点,形成测量误差,进而造成拟合平滑曲线的偏移。 图7 当窗宽为9时原始数据与平滑数据的残差 当窗宽继续增加,其异常值识别效果与图7基本相同,所以该方法在窗长≥9时都可以识别轮廓中的孤立型异常值,并将轮廓两端,特别是右侧异常间断数据点加以识别。 在激光视觉测量过程中,可能存在多个孤立异常值,对异常值识别提出了更高的要求。由上节可知,移动均值法识别多孤立异常值基本无法实现,所以仅对稳健局部加权回归法识别多孤立异常值的能力进行验证。 在原有轮廓的基础上增加多个随机孤立异常值,对其进行异常值识别,识别效果如图8所示;原数据与平滑数据的残差值,如图9所示。 图8 当窗宽为9时RLWR法识别多孤立异常值 图9 当窗宽为9时原始数据与平滑数据的残差 由图8,9可见,在移动窗长为9时,基于稳健局部加权回归的异常值识别法,能将所有孤立异常值以及右端的异常数据识别,展现出较强的多孤立异常值识别能力。 在此采用图6和图8的识别结果,剔除异常值,利用非线性最小二乘法进行椭圆拟合;同时对保留异常值的原轮廓进行拟合,最终得到异常值去除前、后的轮廓拟合对比结果,如图10、图11所示。 图10 原始轮廓异常值处理前、后的椭圆拟合效果 图11 多孤立异常值剔除前、后的椭圆拟合效果 依据测量数据和拟合结果计算出异常值剔除前后的拟合椭圆参数,如表1所示。结合图、表分析剔除异常值前、后的拟合椭圆。观察图10,原始轮廓异常值处理前、后的拟合椭圆存在较大差异,原始数据的拟合椭圆圆心为“*”,其长轴直径为12.613 2 mm,短轴直径仅为4.875 1 mm,离心率达到0.922 3;而剔除异常值后,拟合椭圆圆心为“+”,长轴直径为19.475 5 mm,短轴直径为18.779 8 mm,离心率为0.264 9,更为符合测量实际。图11为多孤立异常值轮廓在剔除异常值前、后的椭圆拟合效果,在多孤立异常值情况下,轮廓数据已无法进行椭圆拟合,拟合结果不收敛;而采用RLWR法则能有效剔除全部异常值,其拟合椭圆参数与图10剔除异常值后的拟合椭圆参数基本一致。 表1 异常值处理前后的拟合椭圆参数 在椭圆拟合的同时,对轮廓异常值处理前后的拟合误差进行了分析,结果如表2所示。 表2 异常值处理前后的椭圆拟合误差 原始轮廓异常值剔除后,拟合误差大幅减小,其残差平方和SSE由8.452 3×10-6减少到4.983 2×10-7;均方差MSE由1.507 4×10-4减少到3.684 9×10-5;均分根差RMSE则由2.272 1×10-8降为1.357 8×10-9.同样,多孤立异常值的轮廓在剔除异常值后,其拟合误差也大幅减小,与原轮廓异常值剔除后的拟合误差基本一致。上述实验结果说明利用稳健局部加权回归识别法剔除异常值可以使截面椭圆的拟合误差大幅度减小,拟合结果更加精确。 本文采用基于激光视觉的轮廓测量系统对棒材轮廓进行了测量。针对测量中出现的孤立异常值,提出了一种基于稳健局部加权回归的异常值识别法,并与移动平均识别法进行了对比,探讨了不同移动窗宽下的识别效果,及其处理多孤立异常值的能力。随后利用非线性最小二乘法对异常值剔除前、后的数据进行了椭圆拟合,并计算了各拟合椭圆参数和拟合误差。进一步证明基于稳健局部加权回归的异常值识别法相较于移动均值法等传统识别方法,具有较强的异常值识别能力,简便高效,鲁棒性好,对提高激光轮廓在线测量精度具有重要作用。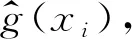

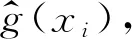
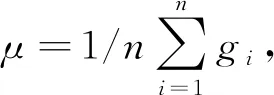
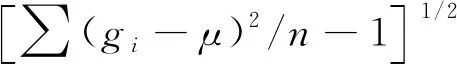
3 激光轮廓的异常值识别实验
3.1 典型轮廓的识别



3.2 多孤立异常值的识别


4 轮廓拟合效果分析


5 结束语
