半径间隔界驱动卷积神经网络模型的图像识别

肖 遥，蒋 琦，王晓明,2*，杜亚军，黄增喜

（1.西华大学计算机与软件工程学院，四川 成都 610039；2.西华大学机器人研究中心，四川 成都 610039）

图像识别是计算机视觉领域的重要研究方向，其任务是识别给定的一张或多张图像的类别或属性。图像识别技术被广泛应用于自动驾驶、视频监控以及智能医疗等领域。实际应用中，图像识别的主要挑战在于如何提取具有强鉴别性的图像特征。传统的图像识别算法针对不同模式的识别任务设计了多种类型的特征[1−3]。然而，这些特征往往只针对某一特定的识别环境，无法完全适应复杂环境。随着计算机硬件的迅速发展及大规模数据集可用性的提高，卷积神经网络（convolution neural network,CNN）在图像识别领域受到越来越多研究者的关注。不同于传统的识别算法，基于CNN 的图像识别能够自适应的提取适合当前识别模式的深度特征，具有更强的泛化性能及更高的识别率。为了进一步增强深度模型的特征表达能力，研究者提出了许多不同的改进方案。按照实现的方式，这些改进可分为基于网络结构的改进和基于能量函数的改进。基于网络结构的改进旨在增加网络的深度以提高深度模型的特征表达能力。文献[4]提出了具有13～19 层网络的VGG 深度卷积模型。文献[5]提出的GoogLeNet 深度卷积模型将网络层数提高到了22 层。文献[6]将网络模型进一步提高到了110 层，并探索了高达1 102 层的网络模型的有效性。增加网络的深度能够增强模型的特征表达能力，然而，这种策略是不可持续的。随着网络层数的增加，深度模型将变得更难收敛。此外，更深的网络需要更多GPU/CPU 集群和复杂的分布式计算平台，以实现具有高计算复杂性的学习，然而在当前计算机硬件性能的限制下，这样的策略不可避免地将会达到极限。

不同于基于网络结构的改进，基于能量函数的改进着手于采用不同的学习策略来指导深度模型的训练。传统的CNN 模型中往往采用Softmax 能量函数指导模型的更新，但这种策略是间接和低效的[7]。针对这一不足，文献[7]采用Triplet 能量函数代替Softmax，然而，该能量函数中锚样本对的构造与选择是一个复杂且困难的过程，会导致模型的训练变得不稳定。文献[8]提出的中心损失能量函数在鲁棒性和模型收敛速度上具有优势，但其应用必须依赖于Softmax 损失。文献[9]在Softmax 中引入了Fisher 判别正则项与旋转不变正则项，增加了图像特征的质量与鲁棒性，但过多的正则项约束使得深度模型的学习变得更加困难。

不同于上述基于能量函数的改进，文献[10]认为支持向量机（support vector machine,SVM）能够提供更出色的正则化效果，提出了一种基于SVM的CNN 模型。与传统的CNN 模型相比，基于SVM 的CNN 最显著的优势在于将大间隔原理引入到CNN 的学习策略中，迫使CNN 更多的关注异类样本特征间的分类间隔，从而提取到具有更强鉴别性的样本特征。然而，它忽略了一关键事实：SVM 的泛化能力不仅取决于不同类别样本之间的间隔，还与特征空间中所有样本的最小包含球（minimum enclosing ball,MEB）的半径有关[11]。实际上，在一般的识别任务中，给定的样本特征往往是不变的，MEB 的半径是一个固定的常数。在CNN 模型中，训练样本的特征会随着网络参数的更新而变化，MEB 的半径也随之发生改变。基于SVM 的CNN 模型中未考虑到这一变化，导致SVM 泛化能力不足，进而限制了其对CNN 正则化效果的提高。

针对上述不足，本文提出了一种半径间隔界（radius margin bound,RMB）驱动的CNN 模型。与传统的CNN 相比，半径间隔界驱动的CNN 采用了更严格的学习策略，不仅考虑了不同类别的样本特征间的间隔，还进一步考虑了不断变化的MEB 的半径对SVM 泛化能力的影响。本质上，通过在学习策略中引入SVM 的泛化误差界理论，本文模型中的CNN 能够扩大不同类别的图像特征间的分类间隔，同时减小包含所有图像特征的MEB 的半径。换言之，迫使CNN 在增大类间间隔的同时减小类内间隔，从而能够提取到更高质量的特征。此外，作为一种基于能量函数的改进方案，本文模型能够显著提高深度卷积模型的泛化能力而不会额外增加网络的复杂度，且不受限于某一特定的网络结构，能够应用于不同的深度模型中。在多个公开数据集上的实验结果表明，半径间隔界驱动的CNN模型能够提取到鉴别性更强的图像特征，在识别应用中表现出了更高的识别率。

1 相关工作

为了建立半径间隔界驱动的CNN 模型，本章首先阐述SVM 及其泛化误差理论，然后介绍基于SVM 的CNN 模型。

1.1 SVM 与泛化误差

SVM 是一种典型的基于大间隔的分类算法，其目标是在给定的特征空间中寻找一个最优分类超平面，使得特征空间中正负样本间有最大的分类间隔。对于一组线性可分的训练样本{x1,···,xn}，SVM 的优化问题可表示为:

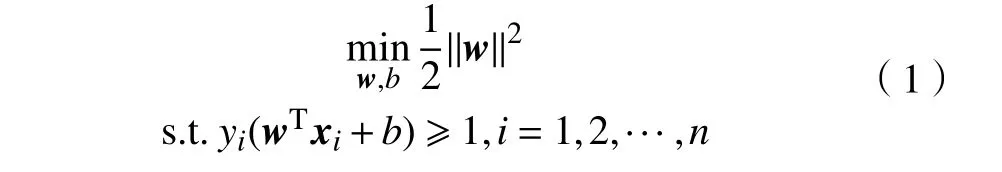
式中：yi∈{+1,−1}是对应的训练样本的标签；n表示训练样本的个数；||w||=1/γ为特征空间中正负样本分类间隔 γ的倒数；b为对应的偏置项。为了选择有效的分类参数，使SVM 在数据集上取得更好的分类表现，VAPNIK 等[12]提出了留一法(leave-oneout,LOO)误差估计用于评估SVM 的泛化性能。LOO 误差被定义为

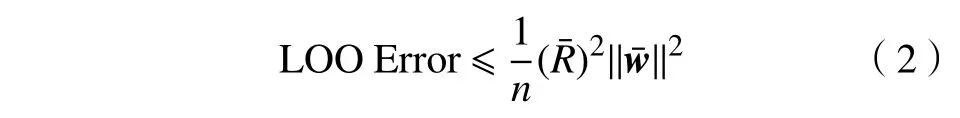
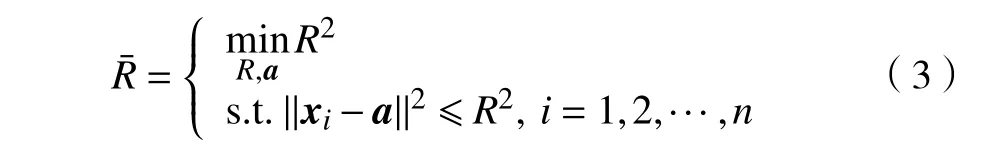
式中a为MEB 的中心。由式（2）可知，SVM 泛化误差上界不仅取决于正负样本间的分类间隔，还与特征空间中包含所有样本的MEB 半径有关。

在一般分类任务中，给定的训练样本往往是线性不可分的，对于此类情况，定义L2 范数SVM的优化问题为：

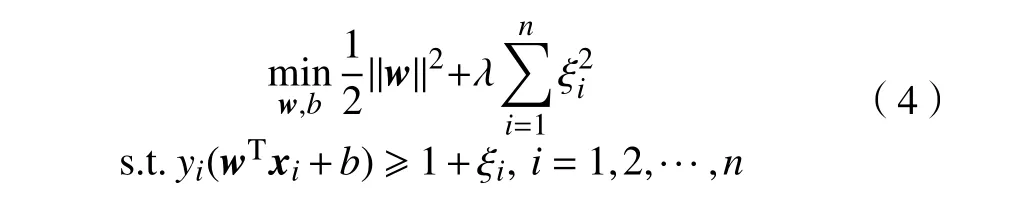
式中：ξi为引入的松弛变量；λ为惩罚系数用于表示模型对分类误差的容忍度，当λ=0时为线性可分的情况。实际上，根据文献[13]，L2 范数SVM 可以被转换为一个等价的硬间隔SVM 问题。

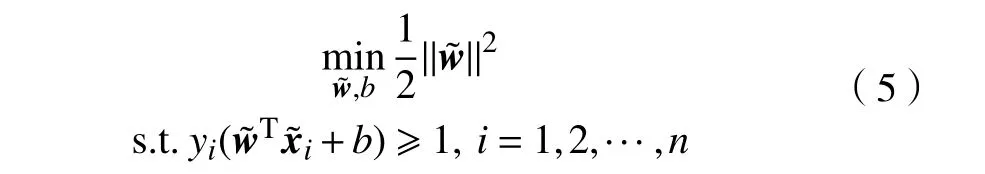
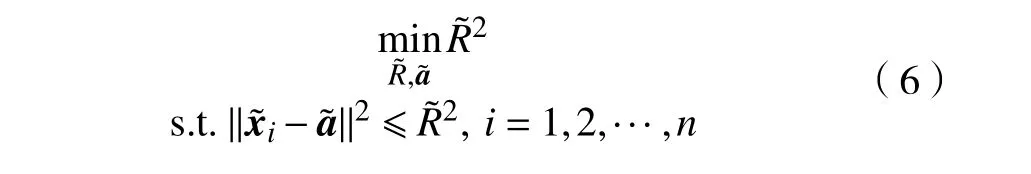
1.2 基于SVM 的CNN 模型

传统的CNN 模型中往往采用Softmax 能量函数指导模型的学习。给定一组包含C个类别的训练样本，则Softmax 能量函数可表达为

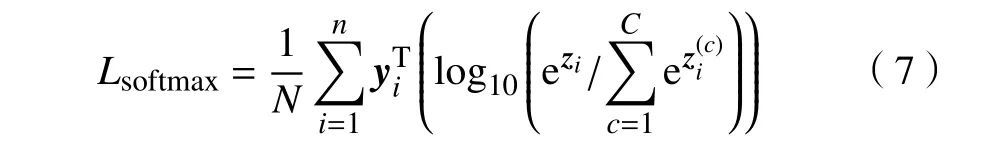
式中：zi=wTϕ(xi;ω)+b为模型中Softmax 层的预测输出；w是模型中预测层的权重系数；ϕ(xi;ω)为模型提取到的样本xi的图像特征；ω表示网络中的权重系数；表示样本zi中的第c个元素；yi是对应样本的标签向量；N表示样本的个数。显然，式（7）只考虑了模型的经验风险，其正则化效果有限。针对这一不足，文献[10]提出了一种基于SVM 的CNN模型。该模型通过结合L2 范数的SVM，将大间隔原理引入到了CNN 模型中。基于SVM 的CNN定义了能量函数，为

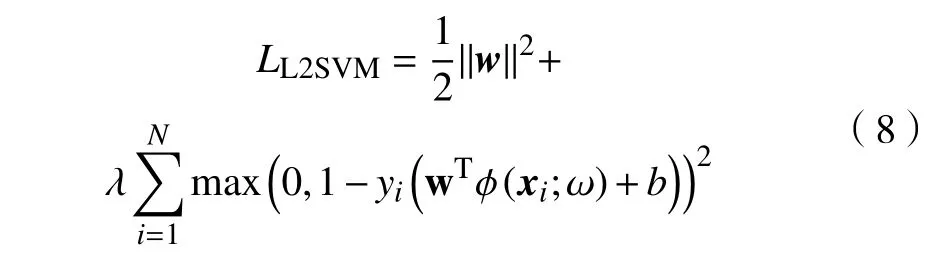
式中：||w||2是分类间隔项，越小则表示不同类别的图像特征间的间隔越大；max(·)2表示二次方的合页损失用于度量卷积深度模型的识别误差，该项越小则表明模型的识别误差越小。与式（7）相比，基于SVM 的CNN 模型额外考虑了不同类别的样本间的间隔，能够提取高质量的图像特征。

2 半径间隔界驱动卷积网络的目标识别

本章的目的在于建立半径间隔界驱动的CNN模型，首先构建二分类模式下的模型，并进一步推广到多类别的模式中；其次详细说明所提模型的训练策略；最后给出模型的识别方法。

2.1 模型的构建

基于SVM 的CNN 模型通过结合L2 范数的SVM，将大间隔原理引入到了深度模型中。相比于传统的基于Softmax 的CNN 模型，基于SVM 的CNN 在识别中表现出了更好的泛化能力。然而，其忽视了一个关键事实：SVM 的泛化性能不仅取决于异类样本特征间的间隔，还与包含所有样本特征的MEB 的半径有关。实际上，在一般分类任务中，确定了特征提取器后，训练样本的特征就不再变化。包含所有样本特征的MEB 的半径随之被固定为一个常数。由式（2）可知，此时SVM 的泛化误差只取决于异类样本间的分类间隔因此不必考虑MEB 的半径。然而，在基于CNN 的深度模型中，作为特征提取器的CNN 会随着权重系数的每一轮更新而改变，由所有样本特征决定的MEB 的半径在不断变化。在这种情况下，如果仍忽略MEB 的半径对SVM 泛化能力的影响，会导致分类间隔只是简单的随着的增大而增大，而无法对SVM 泛化性能的提升做出有效的贡献。换言之，CNN 提取到的样本特征虽然具有更大的类间间隔，但其类内间隔也更大，显然，这样的特征并不能有效提高深度模型的识别能力。

针对上述不足，基于SVM 的泛化误差界理论，本文提出了一种半径间隔界驱动的CNN 模型。为了同时考虑不同类别的图像特征间的间隔和MEB 的半径，所提模型中定义的能量函数为

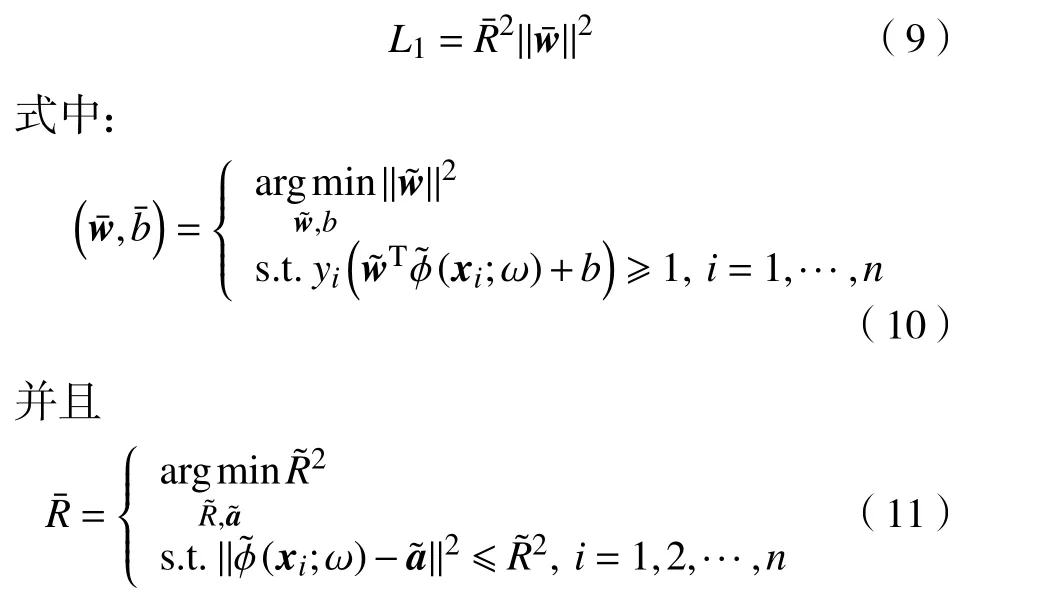
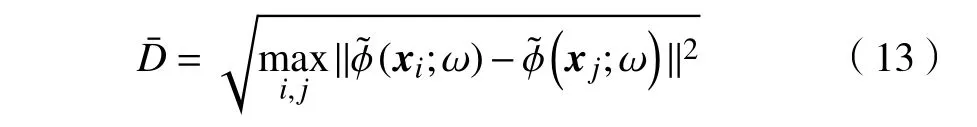
化简式（13），可得

本质上，这是一个简单的求图像特征间最大距离的问题，只需要遍历图像特征便可求得的值。显然，相对于求解复杂的对偶优化问题，求解最大成对距离可以有效地减小模型的计算开销。采用替换式（9）中的，得到改进后的能量函数，为

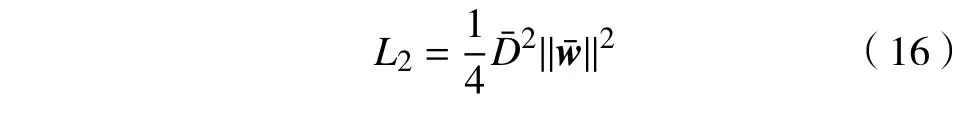
在实际应用中，识别处理的图像往往远大于2 个类别。因此，本文将提出的深度模型扩展到多类别的模式。借鉴文献[14]中一对多的策略，本文分别学习每个类别间的分类间隔的倒数及其对应的最大成对距离。对于给定的一组包含C个类别的训练样本，令{y1,···,yn}表示对应样本的标签，yi∈{1,···,C}。由此扩展能量函数（16）到多类别的模式，为

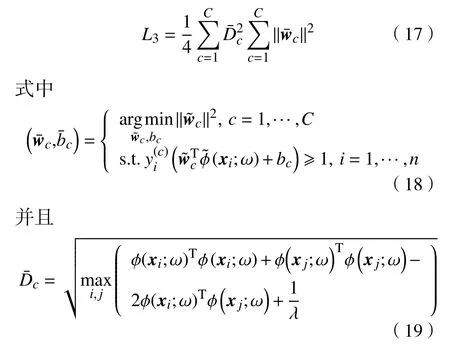
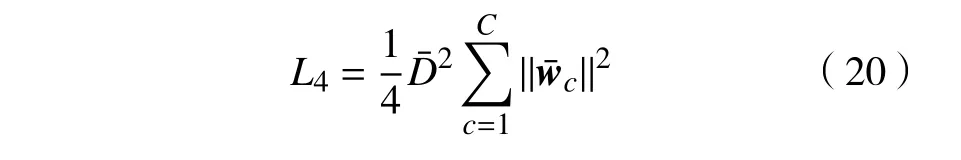
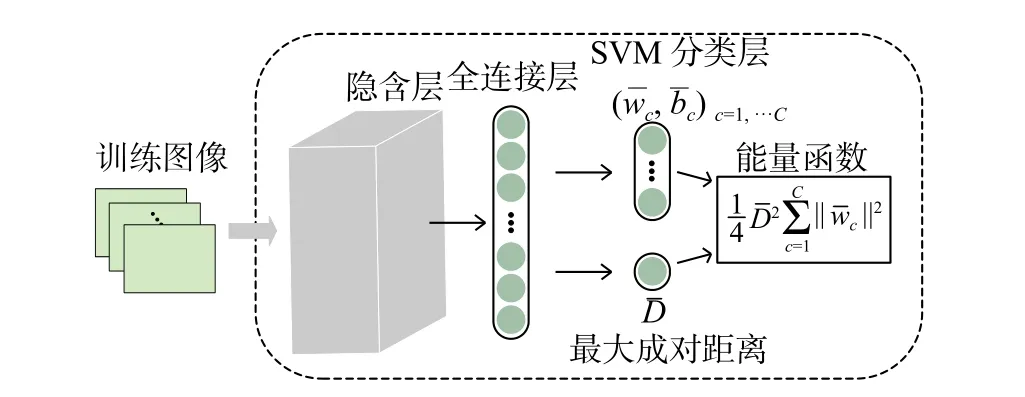
图1 本文卷积深度模型的结构

2.2 模型的更新

本节将介绍半径间隔界驱动的CNN 模型中各个参数的更新，包括卷积网络中的权重系数 ω、分类器参数以及最大成对距离。更新过程采用交替优化的策略，将深度模型分为3 个部分进行更新：固定 ω与更新固定ω 与，更新固定与更新 ω。

2.2.1 更新最大成对距离

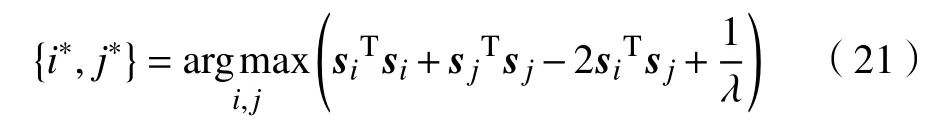
式（21）是一个寻找样本间最大间隔的问题，简单地遍历图像特征就可求得该问题的解。求得{i∗,j∗}后，通过计算式（22）便可得到D¯的值。

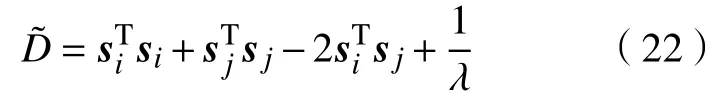
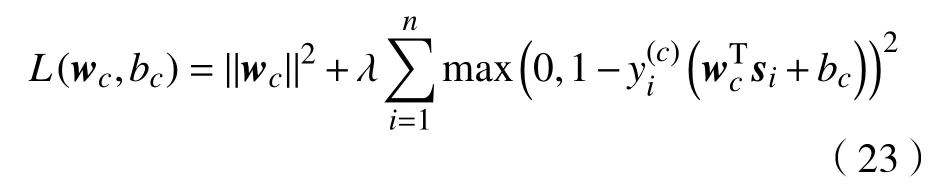
其中si=ϕ(xi,ω)。该无约束问题是关于wc和bc可导的[13]，因此，可通过梯度下降法对其进行求解。为了便于表述，将问题式（23）改写为

得到梯度后，通过梯度下降法便可求得wc与bc在卷积深度模型中的局部最优解。

2.2.3 更新权重系数ω

其中∂si/∂ω表示反向传播，可由深度学习框架如TensorFlow 以及Caffe 等提供的自动微分技术进行计算。最后，能量函数关于权重系数 ω的梯度为

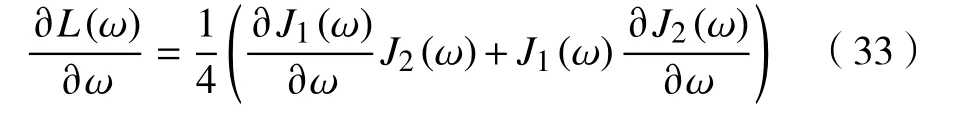
利用式（33），在反向传播的过程中，通过梯度下降法即可实现对卷积网络中各权重系数的更新。

图2 示出了本文提出的深度模型的更新过程。其中步骤（a）表示更新分类器参数以及最大成对距离，步骤（b）表示更新卷积网络中权重系数 ω。

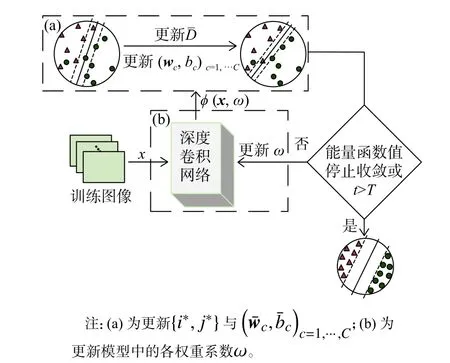
图2 本文提出的深度模型的更新过程

综合所提模型的更新步骤，概括半径间隔界驱动的CNN 模型的学习过程如下。

输入：训练样本X∈Rm×n,训练样本的标签Y∈Rn，设置惩罚系数λ，学习率 σ以及最大迭代次数T。

步骤3：通过式（26）与式（27）更新分类器参数wc与bc。

步骤4：通过式（20）计算能量函数的值。判断，若能量函数停止收敛或迭代次数t＞T，则终止迭代，否则继续进行步骤5。

步骤5：通过式（33）更新权重系数 ω。返回步骤1）继续迭代。

2.3 识别方法

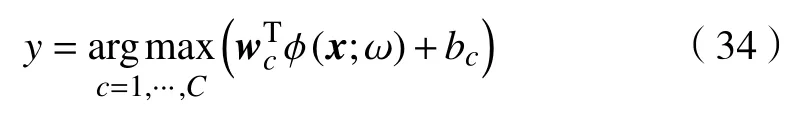
3 实验设计与结果分析

为了综合评价本文提出的半径间隔界驱动的CNN 模型，本章首先分析了不同的惩罚系数λ对所提模型性能的影响，然后通过可视化的方式将所提模型提取的图像特征与传统CNN 及基于SVM 的CNN 提取的图像特征进行比较，最后基于3 种具有代表性的深度卷积网络结构，在多个标准数据集上进行了仿真实验，以验证所提模型在识别率上的有效性。本文中所有的实验都在Nvidia TITAN X(Pascal) GPU 以及Intel(R) Xeon(R) W-2125 CPU环 境中进行。

3.1 惩罚系数对模型性能的影响

半径间隔界驱动的CNN 模型中，惩罚系数λ被用于度量模型对误差的容忍度。为了调查其对模型性能的影响，本节基于ResNet-18 网络结构[5]在数据集CIFAR-10[15]上对多个不同的 λ进行仿真实验。CIFAR-10 数据集包含了10 个类别的真实图像，由5 万张训练图像以及1 万张测试图像组成，每个图像均为32×32 大小的RGB 彩色图。实验中设置惩罚系数λ ∈{0.001,0.01,0.1,1,10,100}，采用Mini-batch 策略，设置每次迭代中使用250 张训练图像，规定最大迭代次数t=2 000。为了使模型尽可能的收敛，采用梯度学习率策略，具体设置为：若迭代次数t＜500，则学习率σ=10−3；若500 ≤t＜1 500，则σ=10−4；若1 500 ≤t＜2 000，则σ=10−5。图3 示出了在不同惩罚系数λ下能量函数值的收敛曲线、识别率的增长曲线。图4 示出了模型在CIFAR-10 数据集上取得的最大识别准确率。从实验结果中可以看出：在λ=0.01 时能量函数的收敛速度最快，模型取得了最高的识别率；随着惩罚系数λ的增大，能量函数的收敛速度变慢，对应的识别率的增长明显变缓，模型也难以取得较高的识别准确率。分析其原因，过大的惩罚系数使得深度卷积模型过多的关注被错误识别的样本，迫使模型拟合更复杂的网络参数以尽可能多地修正被错分的训练样本，这增加了模型的优化难度，同时导致模型出现过拟合。根据实验结果，设定本文实验中的惩罚系数λ=0.01。

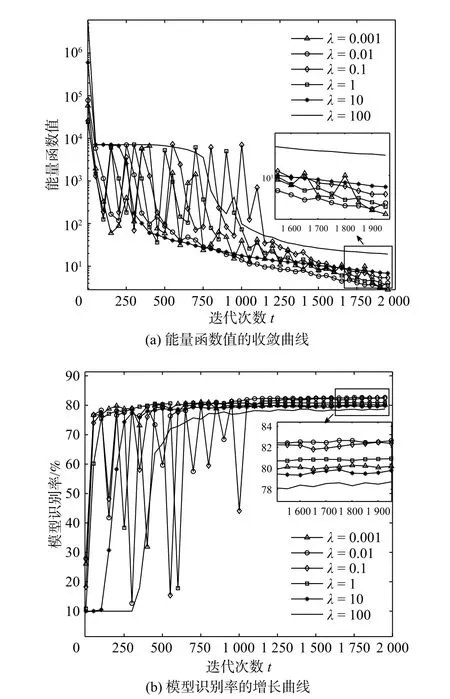
图3 不同的惩罚系数对模型的收敛和识别率的影响

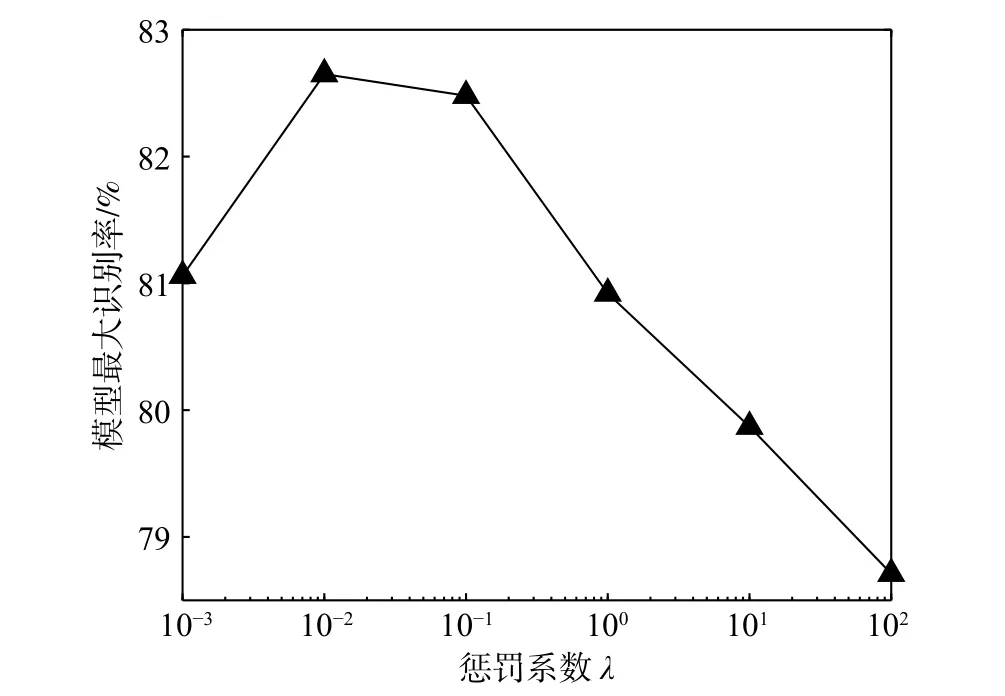
图4 不同惩罚系数下模型的最大识别率

3.2 图像特征可视化分析

为了验证半径间隔界驱动的CNN 模型能够提取到鉴别性更强的图像特征，本节在CIFAR-10 数据集上通过可视化的方式将所提模型提取的图像特征与基于中心损失、基于Softmax 以及基于SVM 的深度卷积模型提取的图像特征进行比较。其中，比较的图像特征提取于CIFAR-10 数据集中全部的测试样本。同时，为了调查本文提出的模型在不同网络结构中的泛化能力，实验中采用AlexNet[16]、VGGNet-13[4]以及ResNet-18[5]3 种具有代表性的网络结构。由于深度模型提取的特征为高维的图像特征，实验先通过TSNE 降维算法[17]，将图像特征的维度降到二维后再进行可视化比较。

图5 示出AlexNet、VGGNet-13 以及ResNet-18在3 种损失函数驱动下提取到的图像特征的可视化结果。其中：xxx-Center 表示基于中心损失的深度卷积模型；xxx-Softmax 表示基于Softmax 的深度卷积模型；xxx-SVM 表示基于SVM 的深度卷积模型；xxx-RMB 表示半径间隔界驱动的深度卷积模型。

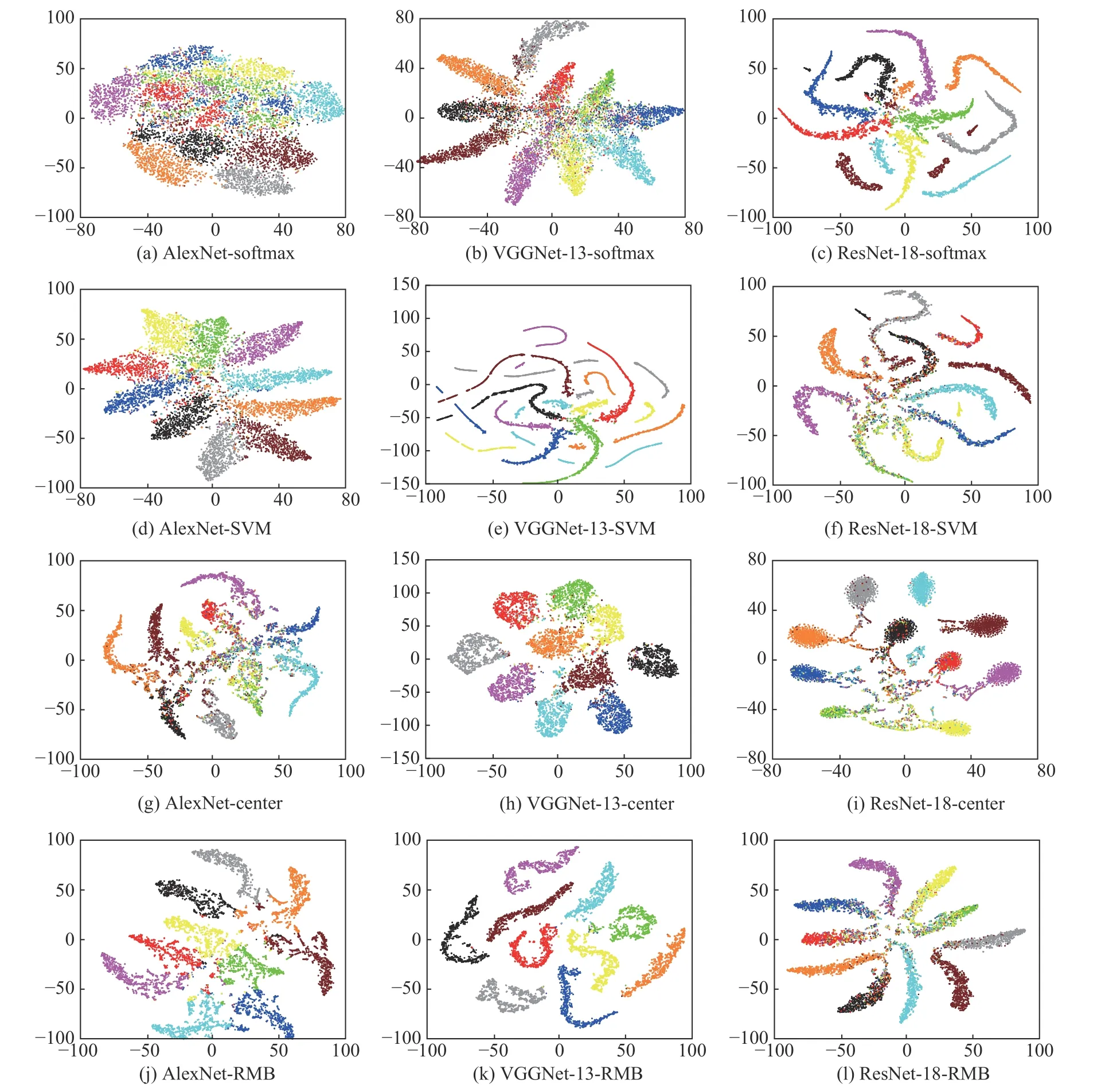
图5 各卷积深度模型提取的图像特征的可视化比较

从实验结果可以看出：与另外3 种深度模型相比，半径间隔界驱动的深度卷积模型能够有效分隔不同类别的样本，得到线性可分的图像特征，从而提取到更高质量的图像特征；基于Softmax 的深度卷积模型难以分隔不同类别的图像特征，并且提取的同类样本特征的分布较为分散；基于SVM 的深度卷积模型能够提供较大的类间间隔，对不同类别的样本的分隔能力相对较差，使得图像特征间线性不可分；基于中心损失的深度卷积模型能够聚合同类图像特征，减小了类内间隔，但其难以分隔不同类别的图像特征。综上，半径间隔界驱动的深度模型在图像特征表达上是非常有效的。

3.3 实验结果与分析

为了验证本文所提出的深度卷积模型在识别率上的有效性，本节在5 个大规模数据集上进行仿真实验。使用的数据集包括2 个数字识别数据集MINIST[18]和SVHN[19]、1 个表情识别数据集FER2013[20]，以及2 个相对复杂的真实图像数据集CIFAR-10[15]和CIFAR-100[15]。其中：MINIST 与SVHN 都是由0-9 这10 个类别的数字图像组成，MINIST 为简单的手写数字数据集，包含的图像是28×28 尺寸的灰度图，SVHN 是相对复杂的街景数字数据集，由尺寸为32×32 的RGB 彩色图组成；FER2013 由7 个类别的表情图像组成，每个图像都是48×48 的灰度图；CIFAR-10 和CIFAR-100 由相同的从真实世界收集的图像构成，这些图像均为32×32 的RGB 彩色图，CIFAR-10 将其分为了10 个类别，CIFAR-100 进一步将这些图像细分成了100 个不同的类别。为了规范数据集中的图像，使用时，本文首先将MINIST 和FER2013 中的图像尺寸缩放到32×32 大小，然后对所有数据集中的图像做归一化处理。实验中，采用3 种具有代表性的卷积网络结构 AlexNet、VGGNet-13 以及ResNet-18，使用TensorFlow 深度学习框架搭建对应的网络结构，使用Top-1 和Top-5 正确率作为模型识别性能的评价指标[21]。Top-1 正确率表示深度卷积模型输出的预测向量中响应最大的那个类别就是测试图像真实类别的准确率。Top-5 正确率则表示预测响应最大的前5 个类别中包含真实类别的概率。所提深度模型中的惩罚系数根据3.1节中的结论进行设置，基于SVM的深度模型与基于中心损失的深度模型中的相关参数参考文献[10]和文献[22]进行设置。实验中的剩余参数采用与3.1 节中相同设置，包括设置最大迭代次数、梯度学习率以及Mini-batch 策略。

表1-2 示出了基于Softmax 的深度卷积模型、基于中心损失的深度卷积模型、基于SVM 的深度卷积模型以及半径间隔界驱动的深度卷积模型在5 个大规模数据集上的Top-1 识别率和Top-5 识别率。从实验结果可以看出，相比于另外3 种类别的深度卷积模型，半径间隔界驱动的深度卷积在所有测试数据集的Top-1 以及Top-5 识别率上均取得了最好的表现，尤其在类别最多且最复杂的CIFAR-100 数据集上表现出了最显著的识别率，其中：与次优的基于中心损失的深度卷积相比，半径间隔界驱动的CNN 模型在CIFAR-100 的Top-5正确率上对AlexNet 的增益为0.03%，对VGGNet-13的增益为0.63%以及对ResNet-18 的增益为1.28%；同时在Top-1 正确率上对AlexNet、VGGNet-13 以及ResNet-18 的增益分别为3.40%、2.90%以及3.66%。实验结果验证了所提模型在识别率上的有效性。此外，观察深度卷积模中的参数总量可知，所提模型能够应用于不同的网络结构中，并且不会额外增加网络结构的复杂度。

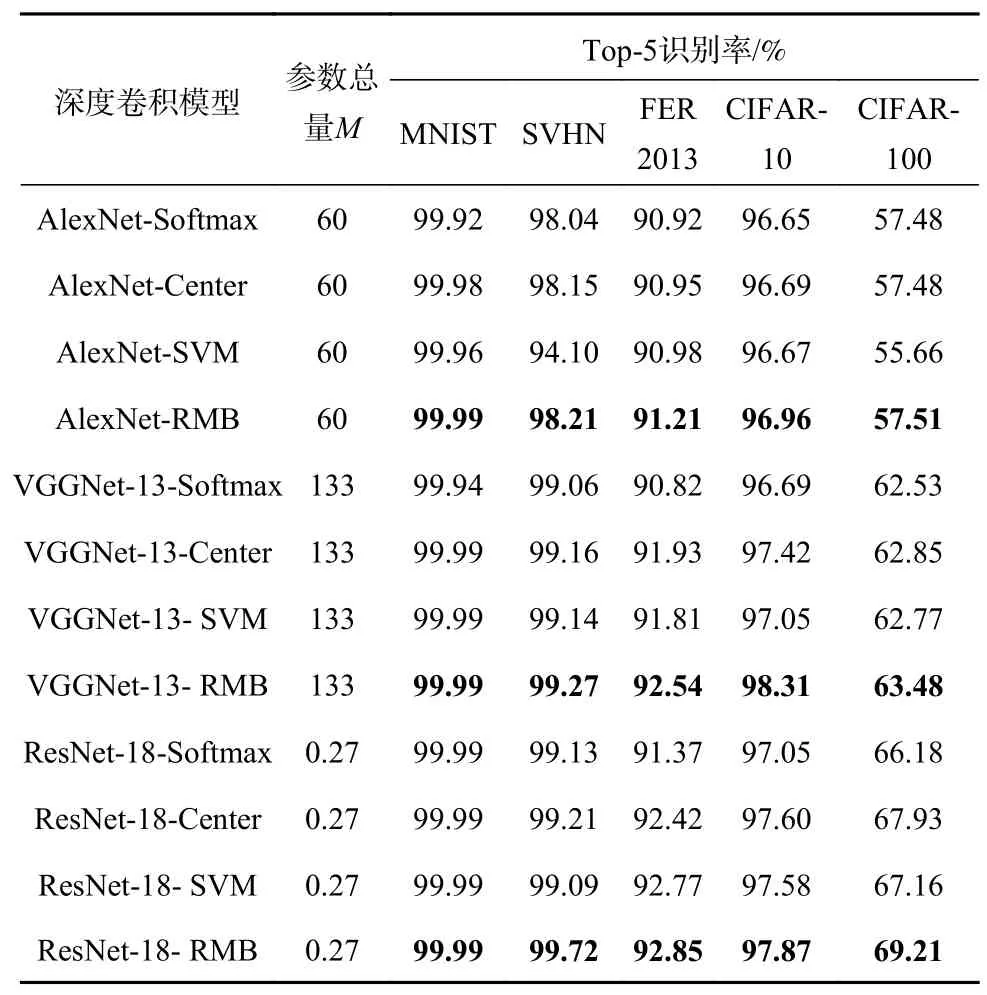
表1 各深度卷积模型的参数总量和在5 个所使用的数据集上的Top-5 识别率比较

表2 各深度卷积模型的参数总量和在5 个所使用的数据集上的Top-1 识别率比较

4 结束语

为了提高CNN 的图像特征表达能力并增强其在识别应用中的泛化性能，本文基于SVM 的泛化误差理论，提出了一种半径间隔界驱动的CNN 模型。该模型采用基于SVM 泛化误差界的准则来指导CNN 深度模型学习和相应分类器构建，其不仅考虑了大间隔原理，还进一步考虑了包含所有训练样本的MEB 的半径对SVM 泛化能力的影响。在多个大规模数据集上的实验结果表明，相对于传统CNN 模型、基于SVM 的CNN 模型以及基于中心损失的CNN 模型，该模型够提取到鉴别性更强的图像特征，并且在图像识别中具有更高的识别率。同时，该模型具有较强的泛化能力，能够被应用于不同的网络结构中，因此，下一步的研究方向是探索所提深度卷积模型在其他模式中的应用，如目标检测、目标追踪以及行为识别等。