考虑时滞的磁流变半主动悬架控制
2021-03-19张志勇王建波蒋文杰李博浩
张志勇,王建波,蒋文杰,李博浩
(1.机械装备高性能智能制造关键技术湖南省重点实验室,长沙理工大学,湖南 长沙 410114;2.长沙理工大学汽车与机械工程学院,湖南 长沙 410114)
随着车辆工业的发展,在设计生产的过程中,除了满足最基本的安全性及操纵稳定性的前提,行业内对车辆的平顺性及舒适性也有了日益严苛的要求[1−2]。在传统被动悬架逐渐难以完全满足需求的情况下,出现了能根据控制策略调整悬架特性的主动悬架和半主动悬架,并逐渐应用于现代汽车中[3]。其中由于半主动控制悬架系统能耗低、控制效果好、结构简单和可靠性高等优点,成为现阶段最有前景的一种可控悬架系统[4]。目前,半主动悬架中运用最广泛的是磁流变半主动悬架,其主要元件是磁流变阻尼器,通过改变该阻尼器的外加电压或电流可以影响其内部磁流变液的外加磁场,进而改变磁流变液中磁性颗粒的黏滞特性,宏观表现为磁流变阻尼器阻尼的改变。因此,可通过改变磁流变阻尼器的电压或电流来实现悬架性能的调整,具有控制方式简单、能耗低等优势[5]。但由于阻尼器中磁流变液的非线性及磁滞特性,难以获得描述精确的正向及逆向参数化模型,这也是实现磁流变悬架半主动控制的难点之一[6]。并且,磁流变阻尼器在接受控制电信号后,从内部磁励线圈实现磁场的激发到磁流变液中磁性颗粒受磁场影响改变黏滞特性之间存在一定的响应时间,这段时间称为磁流变阻尼器的响应时滞,响应时滞的大小与阻尼器元件的结构、尺寸、磁励线圈参数及驱动电路密切相关[7 − 8]。磁流变阻尼器的响应时滞也是悬架控制中值得重点关注的问题。
磁流变悬架实现半主动控制的方式是根据车身及路面状态调整悬架阻尼特性,进而提升悬架性能。但悬架阻尼力具体的调整数值则需依靠特定的控制策略计算获得,目前常见的悬架控制策略包括天棚阻尼控制[9]、PID 控制[10]、滑模控制[11]、鲁棒控制[12]等。然而,从传感器数据的采集到控制策略的计算,再到磁流变液的黏滞特性响应,这一控制流程中,必定会存在一段时间的间隔,也即控制时滞。为了使悬架半主动控制效果更加理想,控制时滞的影响需在控制策略的设计阶段就必须加以考虑。在现有的控制系统时滞稳定性条件中,根据是否依赖系统中时滞的大小,可以分为时滞独立和时滞依赖两种。陈长征等[13]针对具有变时滞控制输入的悬架系统,利用鲁棒H∞控制方法设计出了具有时滞依赖特性的多目标控制策略。该策略在所设计的时滞界限内效果明显,悬架性能大幅提升,但在超过一定界限的大时滞条件下却较为敏感,甚至会出现控制失效现象。高小林等[14]在对悬架进行控制的同时分析了时滞依赖条件下决定临界时滞量大小的影响因素,为改善悬架控制性能提供了新思路。时滞依赖条件下,控制策略的稳定性很大程度上取决于所设计的时滞界限的范围,而时滞独立条件下却没有这种限制。Xu 等[15]针对存在时滞的控制系统给出了不限制延时界限的控制算法,并通过数值算例验证了算法的有效性。Davies 等[16]研究了具有无限时滞的时滞微分系统的稳定性问题,利用李雅普诺夫方法,从线性矩阵不等式(LMI)出发,得到了无穷时滞系统稳定的时滞独立充分条件,然后利用所得到的线性矩阵不等式的可行解,设计了状态反馈控制器。该控制器虽然可在任意时滞量下保持系统稳定,但控制效果却存在一定保守性。
为了提升车辆的舒适性,本文以1/4 车辆动力学模型为对象,采用磁流变悬架进行半主动控制。针对磁流变阻尼器由于存在非线性及磁滞特性而难以得到精确描述的数学模型这一问题,采用BP 神经网络的方法建立了阻尼器的逆模型。为了实现悬架的半主动控制,根据鲁棒H∞控制理论设计出了具体的控制策略,针对控制过程中存在的时滞问题,从时滞独立稳定性条件及时滞依赖稳定性条件两个方面进行了分析,并通过数值仿真对比了两种时滞情况下控制策略的控制性能。
1 带磁流变阻尼器的1/4 车辆动力学模型
根据1/4 车辆振动时的受力情况,可将振动模型简化为车身二自由度模型。该模型主要考虑了车身质量、悬架弹簧刚度、悬架阻尼、车轮质量及轮胎刚度。二自由度模型能够非常准确地描述车身及车轮的振动状态,可运用在绝大多数车辆动力学分析中,也称为车身与车轮双质量系统模型。由于悬架中采用了磁流变阻尼器,该阻尼器除了自身的黏滞阻尼力,还具有由电磁信号产生的库伦阻尼力,具体如图1 所示。

图1 1/4 车辆动力学模型
根据动力学分析及牛顿第二定律可知,该1/4车辆动力学模型的运动微分方程为:
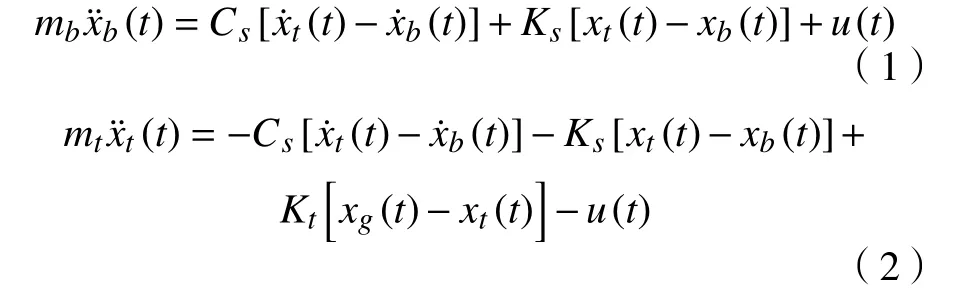
式中:mb为 簧上质量;mt为簧下质量;Kt为轮胎的刚度;xb、xt和xg分别为车身、车轮和路面的位移;Ks为悬架刚度;Cs作为磁流变阻尼器的黏滞阻尼系数;u(t)为控制力,也即库伦阻尼力,其数值大小可由阻尼器的外加电压控制。由此可知磁流变阻尼器产生的总阻尼力为自身黏滞阻尼力与库伦阻尼力之和。
定义车身加速度为被调输出,状态空间方程形式的1/4 车辆动力学模型为:


在悬架实际控制过程中,由于传感器接收感应数据的灵敏性不高,控制器存在运算周期,以及磁流变阻尼器从内部磁励线圈实现磁场的激发到磁流变液中磁性颗粒受磁场影响改变黏滞特性之间存在一定的响应时间等原因,悬架的控制输出并不是完全实时的,而是存在一定的时间延迟。为了建立更加准确的悬架控制系统,应考虑控制时滞因素。因此,车辆动力学模型的状态空间方程可改写为:

式中,d为控制时滞量。
2 考虑时滞的鲁棒控制H∞控制律设计
磁流变悬架实现半主动控制的过程为:首先,根据车身及路面状态确定出悬架所需的期望控制力;然后,再根据期望控制力的大小调节磁流变阻尼器的控制电压,改变悬架的库伦阻尼力,使得悬架力趋近于期望的控制力。因此,如何获得悬架所需期望力便是半主动控制的关键问题。本文采用鲁棒H∞控制策略来计算悬架的期望力,并且为了得到更加准确、符合实际情况的期望力,在控制策略的设计过程中需考虑控制时滞因素。
在各类控制系统中,时滞现象的存在是极其普遍的,关于如何在存在控制时滞的情况下使得控制系统保持稳定性,是所有控制策略设计的基本需求之一。在现有的时滞系统稳定性条件中,根据是否依赖系统时滞的大小,将控制稳定性条件分为时滞独立和时滞依赖两种。下文将分别在这两种时滞稳定性条件下给出鲁棒H∞控制定理。
2.1 时滞独立型鲁棒H∞控制律
定理1对于具有控制时滞的车辆悬架控制系统(5)—(6),如果存在γ >0,且存在适当维度的正定对称矩阵Q、R和矩阵M,使得矩阵不等式(7)有解,则控制律K能使被控系统(5)—(6)渐近稳定。

式中,Θ=QAT+AQ+R。控制律表示为:K=MQ−1。此时,系统控制力可表示为:u=Kx。
定理1 证明过程如下。首先,定义如下的Lyapunov函数:

式中,P和S均为对称正定矩阵。
然后再定义如下二次型性能指标:

在零初始条件下可以得到:

根据Schur 补的性质,式(12)可改写为

式中,Φ=ATP+PA+S。
再令Q=P−1,R=P−1SP−1,M=KP−1则得式(7)。因此,当存在使式(7)成立的可行解时,该解即可保证∏<0,而∏<0又可以保证(x)<0。由Lyapunov稳定性理论可知,当V˙(x)<0时,被控系统(5)—(6)在基于可行解所得到的鲁棒控制律下渐近稳定。到此,定理得证。
2.2 时滞依赖型鲁棒H∞控制律
定理2 对于具有控制时滞的车辆悬架控制系统(5)—(6),对于给定的时滞界限,如果存在γ >0,且存在适当维度的正定对称矩阵L、V、W、R和矩阵M、N,使得矩阵不等式(14)有解,则控制律K0能在所有的滞后时间时,使被控系统(5)—(6)渐近稳定。

该定理的证明过程同样运用到Lyapunov 稳定性理论,其具体推导过程可参考文献[17]。
从时滞独立型和时滞依赖型鲁棒控制律的表示形式可看出,计算控制律力需要已知状态向量即需要采集簧载质量、非簧载质量和路面激励的位移与速度等信号。这些信号在实际应用中比较难以获取,但可以在本文提出的控制律基础上采用输出反馈控制,或车辆状态估计等方法获取相关信号。
3 磁流变阻尼器逆模型
关于建立磁流变阻尼器的模型,国内外学者进行了大量研究,提出了一些具有不同优缺点的力学模型,主要可以分为参数化模型和非参数化模型。常用的模型有Herschel-Bulkley 模型、Bingham 模型、Bouc-Wen 模型等[18]。本文选择Bouc-Wen 模型进行悬架控制设计,模型具体如图2 所示,其动力学方程式如下:

式中:v为磁流变阻尼器的输入电压;f为模型中磁流变阻尼器的总输出阻尼力;而其他参数(c0a,cob,k0,c1a,c1b,k1,x0,αa,αb,δ,µ,N,n,η)需通过实验数据进行优化得到,文中这些参数的具体数值可参考文献[19]的优化数据。
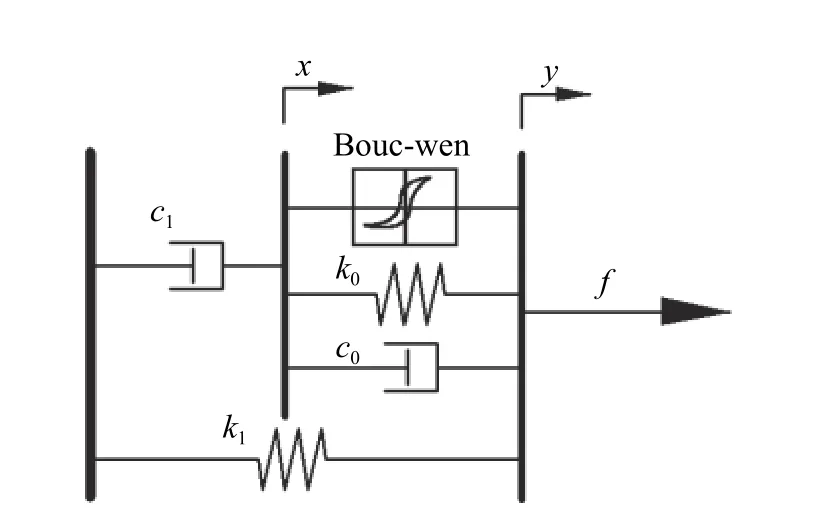
图2 磁流变阻尼器的Bouc-Wen 现象模型
若省略中间过程,磁流变阻尼器的模型可近似为
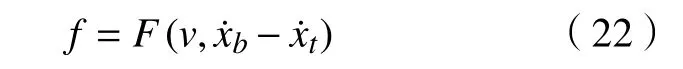
即,磁流变阻尼器的输出力f可近似表示为电压v和阻尼器(车身)速度的函数关系。
在实际的半主动控制过程中,所期望的磁流变阻尼器的输出阻尼力f可由控制律得到,速度可由传感器数据获得,而实现控制所需的控制变量是电压v。因此,需要得到磁流变阻尼器的逆模型,即:
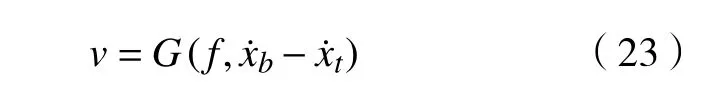
由于磁流变阻尼器的输出阻尼力与速度的关系具有非线性和磁滞特性,加大了磁流变逆模型的参数化建模难度。为了建立能够较为准确地反映出磁流变阻尼器特性的逆模型,本文采用BP 神经网络方法。BP 神经网络算法,也称为误差反向传播法,是诱导学习算法的一种。该算法通过误差来修正网络连接权值,使实际的输出接近期望的输出。根据磁流变阻尼器特性,经过反复测试,本文建立的逆模型如图3 所示。BP 神经网络为3 层,其中输入层有5 个神经元,隐藏层有10 个神经元,输出层有1 个神经元。BP 神经网络具体建立过程如下。
定义神经网络的输入向量为
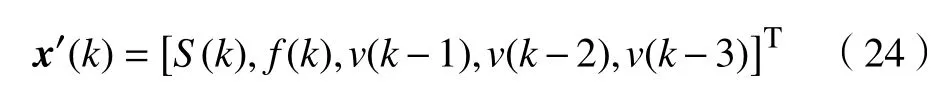
隐藏层的输入为

式中:xi为神经网络输入向量的第i个元素;为输入层神经元的权值;为输入层神经元的偏置量。
隐藏层的激活函数采用Sigmoidal 函数,因此隐藏层的输出为
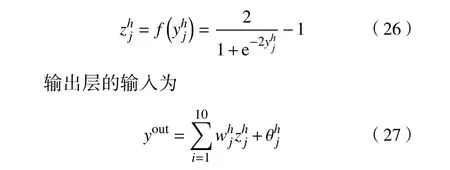
输出层的激活函数采用非线性函数,因此输出层的输出为

磁流变阻尼器逆模型反映了期望力与控制电压之间的关系,与磁流变阻尼器本身的特性有关,但与路面激励、车辆质量分布、车速等因素无关。
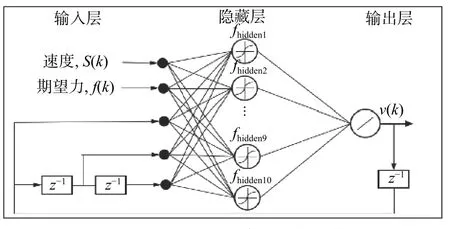
图3 磁流变阻尼器神经网络逆模型
4 控制性能分析
以本文讨论的磁流变悬架为例,运用上节所设计的控制策略对悬架系统进行数值仿真。磁流变阻尼器的初始值为Cs=1 kN/(m/s),悬架的其他参数为:Ks=16 kN/m,mc=690 kg,mt=40 kg,Kt=200 kN/m。分别选择正弦路面和白噪声随机路面谱作为悬架系统的输入激励。其中,正弦路面激励的具体输入信号表示为
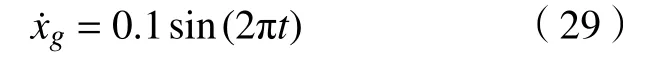
白噪声随机路面激励则以C 级路面谱作为激励输入,路面激励用白噪声表示:

式中:G0为路面不平度系数;U0为车速;ζ(t)为白噪声。此处的白噪声相当于路面激励的速度,其功率谱密度采用下式计算:

在车辆行驶的过程中,车身加速度与舒适性密切相关,故常作为评价汽车舒适性的量化指标。此外,悬架动行程除了能反映乘员的舒适性外也能在一定程度上反映在受到路面激励时悬架的稳定性。为了在验证所设计的考虑时滞的半主动控制策略有效性的同时,了解不同时滞稳定性条件下的鲁棒H∞控制策略效果的区别,本文以车身加速度和悬架动行程作为评价悬架控制性能的指标,进行不同时滞条件下的悬架半主动仿真试验。

图4 车身加速度比较(正弦路面)
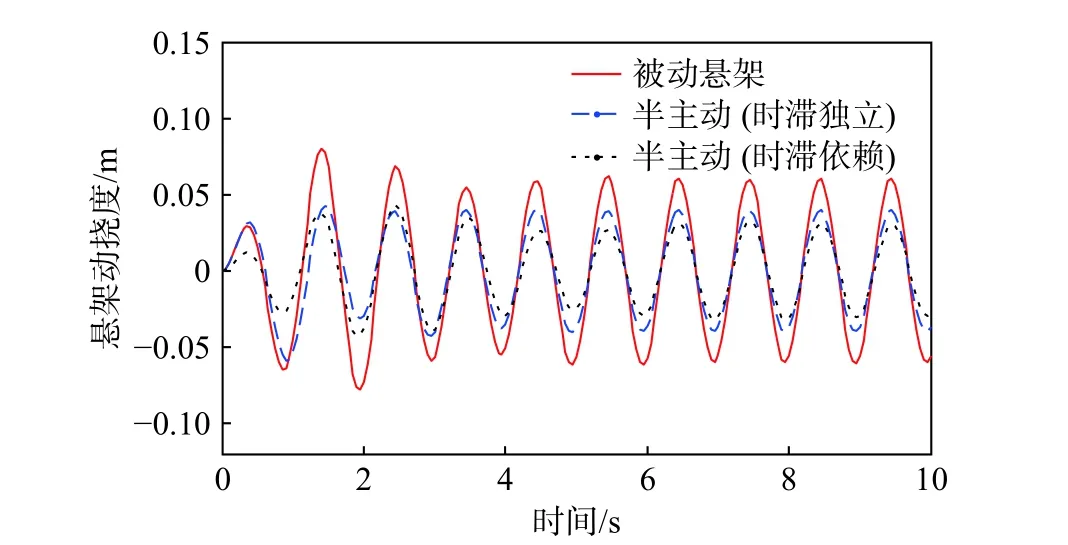
图5 悬架动行程比较(正弦路面)
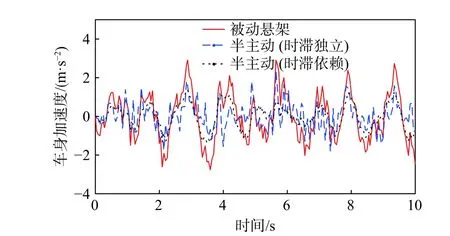
图6 车身加速度比较(白噪声随机路面)
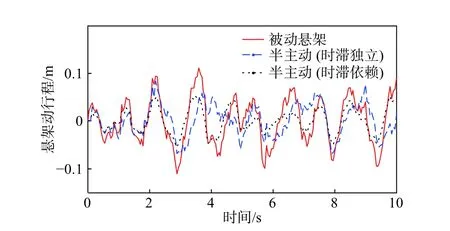
图7 悬架动行程比较(白噪声随机路面)
从图4 和图5 中可以看出,正弦路面激励下,在系统实际延时不超过时滞界限时,相较于被动悬架,时滞独立及时滞依赖条件下的半主动控制策略的控制性能在车身加速度及悬架动行程方面均有所提升,且时滞依赖条件下控制策略的性能提升更明显。
由图6 和图7 可知,白噪声随机路面激励下的控制性能与正弦路面激励下的结果保持一致。
仿真试验中具体性能指标的峰值及均方根值如表1 所示。从表中可知,正弦路面工况下,两性能指标的峰值从被动悬架的1.9459 和0.0798 分别降低到时滞独立控制时的1.0006 和0.0587,时滞依赖控制时的0.7648 和0.0429,时滞独立下降比为48.6%和26.4%,时滞依赖下降比为60.1%和46.2%。两性能指标的均方根值从被动悬架的1.0808和0.0436 分别降低到时滞独立控制时的0.5575和0.0287,时滞依赖控制时的0.4036 和0.0227,时滞独立下降比为48.7%和34.2%,时滞依赖下降比为62.6%和47.7%。在白噪声随机路面工况下,两性能指标的峰值从被动悬架的2.9061 和0.111 5分别降低到时滞独立控制时的2.3141 和0.0834,时滞依赖控制时的1.8760 和0.0651,时滞独立下降比为20.4%和25.2%,时滞依赖下降比为35.4%和41.6%。两性能指标的均方根值从被动悬架的1.2497 和0.0489 分别降低到时滞独立控制时的0.7278 和0.0337,时滞依赖控制时的0.6578 和0.0261,时滞独立下降比为41.7%和31.3%,时滞依赖下降比为47.4%和46.6%。

表1 半主动控制性能指标的峰值及均方根值(实际延时量不超过时滞界限)
当实际延时量大于时滞界限时,即d=0.4 s 时,根据定理2 及时滞界限=0.2 s 的条件,计算出时滞依赖控制律K0,即控制律K0中所反映的时滞界限小于实际延时量。再根据定理1 计算出时滞独立控制律K,其中K的获得不需要时滞界限条件。在白噪声路面激励下分别将两控制律应用到控制系统当中,进行控制性能分析,并将结果与被动悬架对比,如图8 和图9 所示。

图8 车身加速度比较(白噪声随机路面)
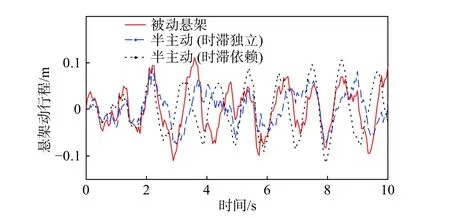
图9 悬架动行程比较(白噪声随机路面)
当系统实际延时超过所设计的控制策略时滞边界时,时滞独立条件下的半主动控制悬架性能依旧优于被动悬架系统,而时滞依赖条件下的半主动悬架性能却变得较差,表现为随着时间的推移,控制性能出现明显恶化现象。
仿真试验中具体性能指标的峰值及均方根值如表2 所示。从表中可知,在白噪声随机路面激励下,时滞依赖条件下半主动悬架的车身加速度和悬架动行程的峰值分别为2.9156 和0.1151,均方根值分别为1.2690 和0.0504,相比于被动悬架基本毫无优势,甚至稍逊于被动悬架。
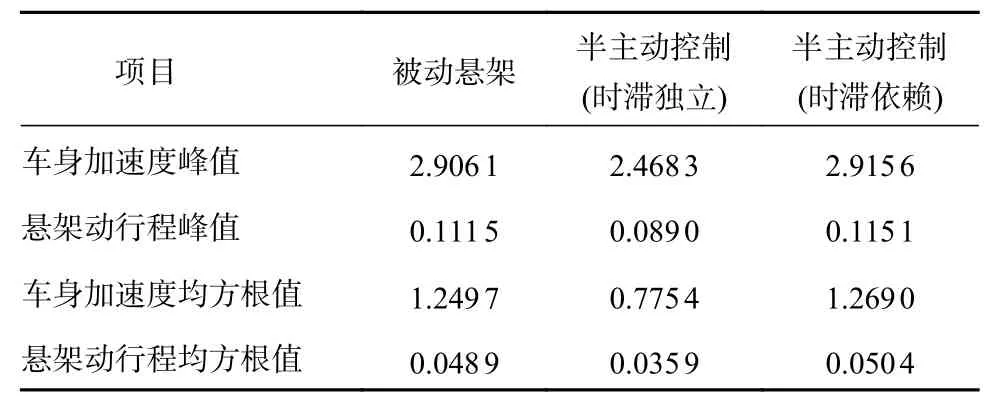
表2 半主动控制性能指标的峰值及均方根值(实际延时量超过时滞界限)
与之形成鲜明对比的是,时滞独立条件下,半主动控制悬架的车身加速度和悬架动行程峰值从被动悬架的2.9061 和0.1115 降低到了2.4683 和0.0890,降幅达15.1%和20.2%,均方根值从被动悬架的1.2497 和0.0489 降低到了0.7754 和0.0359,降幅达37.9%和26.6%,相较于系统实际延时不超过所设计控制策略时滞边界的情况,其降幅保持稳定。
5 结论
1) 以1/4 车辆动力学模型为研究对象,建立了磁流变半主动悬架控制系统,并根据鲁棒H∞控制理论设计了半主动控制策略。数值仿真结果证明,设计的悬架半主动控制策略能改善车辆的平顺性。
2) 当系统实际延时不超过时滞界限时,时滞独立和时滞依赖条件下半主动控制策略的控制性能均优于被动悬架,且时滞依赖条件下的控制性能更明显,说明时滞依赖稳定性条件下的控制策略针对性较强。
3) 当系统实际延时超过时滞界限时,时滞独立条件下的半主动控制性能仍优于被动悬架系统,但时滞依赖条件下的控制性能有恶化趋势,说明时滞独立条件下控制策略具有更好的稳健性。
