云环境中抵御内部关键字猜测攻击的快速公钥可搜索加密方案
2021-03-17陈宁江黄汝维黄保华
陈宁江 刘 灿 黄汝维 黄保华
①(广西大学计算机与电子信息学院 南宁 530004)
②(广西多媒体通信与网络技术重点实验室 南宁 530004)
1 引言
在云计算技术的应用推动下,云服务成为企业或个人减轻应用维护的方式。可搜索加密[1]是解决密文检索的重要方案之一,它允许用户检索包含用户指定关键字的加密文档,其中给定关键字陷门,服务器可以在不解密的情况下找到用户所需的数据。可搜索加密分为对称可搜索加密(Symmetrickey Searchable Encryption, SSE)[2]和非对称可搜索加密(Asymmetric-key Searchable Encryption,ASE)[3]。SSE虽然效率较高,但秘钥分配复杂,适用于一对一的场景。为了解决这一问题,Boneh等人[4]首次提出一种基于关键字搜索的公钥可搜索加密(Public Key Encryption with Keyword Search,PEKS),使用户能够在非对称加密中搜索加密数据。Boneh等人[4]的方案在抵御关键字攻击方面是满足语义安全的[5]。然而,CSP(Cloud Service Provider)是一个诚实且好奇的第三方,在拥有关键字陷门之后,不可避免会通过关键字猜测攻击[6,7]获取密文的关键字信息。由此,产生内部关键字猜测攻击。内部关键字猜测攻击是指由内部攻击者,一般是指可以通过合法手段获取关键字陷门数据的实体,在本文背景中,通常指云服务提供商。外部关键字攻击是指需要拦截方式来获取数据陷门的实体因此相较于外部关键字攻击,内部关键字攻击具有更高的权限和安全性。
PEKS的概念由Boneh等人[4]提出,但是其方案不仅在加密和检索中有较大的计算开销,而且存在许多安全性问题。Byun等人[8]指出关键词空间远小于秘钥空间,提出离线关键字攻击的问题,并成功击破Boneh等人的方案。为了抵御离线关键字猜测攻击,文献[9]和文献[10]分别提出基于倒排索引和无证书认证的抵御关键字猜测攻击的公钥可搜索加密方案。然而,对于方案内部对手仍然有机会成功地发起关键字猜测攻击。文献[11]提出了一种基于模糊关键字搜索的加密方案,该方案能够抵御外部关键字猜测攻击。Rhee等人[12]引入“陷门不可区分性”的安全概念,证明陷门不可区分性是阻止关键字猜测攻击的充分条件。但是,他们的工作都没有解决关键字猜测攻击(Keyword Guessing Attack, KGA)[13,14]是服务器的问题。为抵御服务器关键字攻击问题,Shao等人[15]提出诚实且好奇的服务器问题,采用信息技术签名和权威机构的认证。文献[16]使用代理重加密技术对部分密文进行重加密处理,但需要较大系统开销的方案。以上方案都是基于正向索引,其搜索效率较低。为了提高效率,文献[17]提出不需要认证的概念,在构建索引过程中加入数据拥有者的私钥,任何没有数据拥有者私钥的人都不能生成合法的索引,服务器无法进行正常的攻击。但在考虑到内部关键字攻击中,以上工作都是基于“文献-关键字”的正向索引方式,密文信息的检索时间复杂度与总的密文数成正比。对于加密的文件来说,当密文包含大量的关键字时,这种线性链表索引结构就会大大降低搜索效率。因此,为了在提高检索效率的同时可以抵御内部关键攻击,本文设计了基于并行倒排索引的可以抵御内部关键字猜测攻击的快速公钥可搜索加密方案。利用安全高效的倒排索引[18]实现次线性搜索,其搜索效率只与包含相关查询关键字的密文数成正比。在抵御内部关键字猜测攻击方面,通过加入用户私钥技术来抵御关键字猜测攻击。
针上述问题的描述,本文的主要思路是:
(1) 提出一种抵御内部关键字攻击方案。基于双线性配对的公钥算法,构造了一个完全公钥环境下的可抵御内部关键字攻击的公钥可搜索加密方案。
(2) 提出一种高效的关键字搜索方案。采用快速并行的倒排索引,且加密索引能够抵御内部关键字猜测攻击,提高了系统安全性和搜索效率。
2 PSEFKS方案设计
2.1 系统模型
本文定义的快速安全的公钥可搜索加密(Publickey Security Encryption with Fast Keyword Search, PSEFKS)的系统模型如图1所示,主要由3个实体组成:数据拥有者、数据用户和云服务器。
首先,数据拥有者有一系列数据文档集合f ={f1,f2,···,fn},打算把它存储到云服务器中。为了保证数据的安全且提高用户的搜索效率,数据拥有者构建了一个安全可搜索加密的倒排索引和一系列加密后的密文,然后数据拥有者把安全索引和可搜索密文上传至云服务器。另外,数据用户根据自己的需求,生成包含特定需求的关键字密文陷门;随后,把关键字陷门上传至云服务器,并解密云服务器返回的搜索结果。最后云服务器根据数据用户上传的关键字陷门,与已有的加密密文进行检索匹配,从已有的密文集合中,返回给数据用户包含精确关键字搜索密文的密文集合。
2.2 高效的倒排索引构建
在上述系统模型中,数据拥有者在进行密文上传之前需进行密文关键字索引的构造。具体过程如图2所示。假设密文Cw提 取的关键词集合为Cw= {w1,w2,···,wi}, H为哈希函数,倒排索引是对密文C1,C2,···,Cw等建立的“关键词-文档”索引。每个关键词 wi拥有对应的关键词文档的集合为(wi,value )索引集,其中v alue为关键词所对应的文档集合。Enc( wi||Kwi) 中Kwi表 示关键词wi当前产生的计数器即文档编号值。
在倒排索引中,文档和搜索效率是次线性的,为实现海量数据的快速检索,所以本文采用高效的倒排索引架构来进行密文的搜索操作。基于倒排索引构建的并行加密索引结构,每个关键字都有一个计算器用来记录产生密文的数量。每个密文都由一个关键词和当前计数器值作为输入生成。当kw=1时,说明这是第1次生成的密文w,把w和kw作 为输入,生成密文Cw,kw。然后,将Cw,kw和密文文档集合上传至云服务器。云服务器收到用户的关键字陷门请求时,在倒排索引中找到对应的逻辑地址,得到加密的文档列表。最后,采用用户公钥对加密的文档列表进行逐个解密,得到文档ID集合。由于上述迭代过程可以并行完成,所以一个完整的搜索过程可以并行实现,从而可以在很大程度上减少关键词匹对的次数,从而降低开销,提高搜索效率。

图1 系统模型

图2 高效的倒排索引
2.3 模型的形式化定义
PSEFKS方案主要由2个哈希函数、3个对象和7个概率多项式时间算法组成: Setup, K eyGenDO,KeyGenDU, S trucInit, S trucEnc, T rapdoor, T est。具体的每个算法实现形式如下:
(1) Setup( λ):系统初始化算法。算法以安全参数 λ作为输入,输出系统公共参数Param,由数据拥有者运行。
(2) K eyGenDO(Param):数据拥有者生成秘钥算法。算法以系统公共参数Param作为输入,产生数据拥有者的公/私钥 ( PKDO, S KDO),由数据拥有者运行。
(3) K eyGenDU(Param):数据用户生成秘钥算法。算法以系统公共参数Param作为输入,产生数据用户的公/私钥( PKDU, S KDU),由数据用户运行。
(4) StrucInit(Param):隐藏关系结构初始化算法。运行算法以初始化一个用于加密索引生成的隐藏关系结构。以系统公共参数Param为输入,输出隐藏关系结构 H S= (P RI,PUB),由数据拥有者执行。
(5) StrucEnc( w, P RI, P KDU, S KDO):隐藏关系结构加密即加密索引生成算法。算法以关键字w 、隐藏关系结构P RI 、数据拥有者的私钥S KDO和数据用户的公钥P KDU为输入,生成可搜索的加密索引C Iw并更新P RI,由数据拥有者执行。
(6) Trapdoor( w′, P KDO, S KDU):关键字陷门生成算法。算法生成关键字w′的陷门,然后上传到服务器,进行搜索阶段的匹配工作。算法输入数据拥有者公钥 P KDO, 数据用户私钥S KDU,产出包含特定关键字的陷门信息,由数据用户运行。
(7) Test( Cw, C Iw, P UB, P KDU, P KDO,Tw′):测试算法。云服务器在收到数据用户发送的陷门Tw′后,结合存储在云服务器上的可搜索关键词索引C Iw,运行该算法进行匹配搜索以找出匹配陷门Tw′的密文。算法以可搜索密文Cw、加密索引集CIw、隐藏关系结构的公共部分P UB、数据用户的公钥P KDU和 陷门Tw′为输入,输出为0或1,由云服务器运行。
3 PSEFKS方案构造
3.1 方案构建
PSEFKS方案的具体算法描述如下:
(1) Setup( λ):系统初始化算法。算法以安全参数λ 作为输入,输出系统公共参数Param={p,g,,G,GT,H1,} 。 其中p 是 一个与安全参数λ 相关的最大素数, G,GT是阶为p 的循环阶,g 是群G的生成元,=G× G →GT是一个高效非退化的双线性映射,H1,H2是 两个哈希函数,满足映射关系:H1: {0,1}∗→G , H2:GT→{0,1}logp。
(2) K eyGenDO(Param):数据拥有者生成秘钥算法。算法以系统公共参数Param作为输入,输出数据拥有者的公/私钥对(P KDO, S KDO) =(gx,x),其中x。
(3) K eyGenDU(Param):数据用户生成秘钥算法。算法以系统公共参数Param作为输入,产生数据用户的公/私钥 (PKDU, S KDU) =(gy,y),其中y。
(4) StrucInit(Param):隐藏关系结构初始化算法。算法输入为系统公共参数Param,输出一个隐藏关系结构HS = (PRI, PUB) = (α , gα),其中α以 及P R I 是 一 个 形 如( α,{( w,kw)|w ∈W,kw∈N })的动态列表,初始化为(α )。
(5) KwEnc(ww,SKDO, P KDU,PRI):加密索引生成算法。算法生成文档 w的关键字集wi= (w1,w2,···,wt) 、数据拥有者的私钥S KDO=x和数据用户的公钥P KDU=gy作为输入,通过以下方式生成文档的可搜索密文Cwi:
(a)判断关键字w 的 记录(w ,kw) 是否在P RI中;
(b)如果记录不存在,设置 kw= 1并添加(w ,kw)至P RI ;否则,设置kw=kw+1并 更新P RI;
(c)输出可搜索密文Cwi= (C1,C2),其中
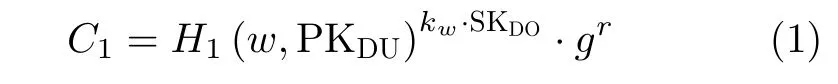

(d)当全部关键字计算完成后,记索引集CIw= (C Iw1,CIw2,···,CIwt),并将含有关键字的密文和索引发送给云服务器。
(6) Trapdoor( w′, P KDO, S KDU):关键字陷门生成算法。算法生成关键字w′的陷门,然后上传到服务器,进行搜索阶段的匹配工作。算法以数据拥有者公钥 P KDO, 数据用户私钥S KDU作为输入,计算关键词的陷门 Tw′=e ︿ (H1(w′)SKDU, P KDO),并将Tw′发送给云服务器。
(7) Test( CIw, Cw, P UB, P KDU, P KDO,Tw′):云服务器在收到数据用户发送的陷门 Tw′后,结合存储在云服务器上的可搜索关键词索引C Iw,运行该算法进行匹配搜索以找出匹配陷门 Tw′的密文。算法以可搜索密文 Cw、 加密索引集C Iw、隐藏关系结构的公共部分P UB=gα、 数据用户的公钥P KDU=gy和陷门Tw′为输入,通过以下步骤搜索匹配的密文集:
(c)在加密索引集 C Iw中查找满足C′=C [i]的加密索引集C Iw=(C1,C2),如果找到,则将该索引对应的密文集 Cw的 密文C [i]加 到C′,另t=t+1,然后继续步骤1;
(d)如果遍历加密索引集 CIw找不到匹配的索引,则输出C′。
通过图3可以看出,在数据用户生成关键字陷门,进行密文搜索时,可以在一次双线性对的时间内匹配到密文集中的搜索关键字。在普通的倒排索引搜索中,在通过关键字陷门匹配到关键字密文集后,需要进行链式访问,会揭露所有的密文信息。在本文隐藏关键字结构的方案中,只有在进行双线性匹配运算时,得到想要的关键字匹配密文,由此,确保了数据密文信息更加安全。接下来,将对PSEFKS方案的安全性进行证明。
3.2 安全性证明
PSEFKS索引方面的安全性证明是建立在(Computational Bilinear Diffie −Hellman,CBDH)难题建设之上的,即当CBDH问题是难解的,索引加密部分是不可区分性安全的(INDistinguishability under Chosen Keywords Attack, IND-CKA)。
图 3 快速倒排索引关系结构图gb,gc,G,GT,,t ),算法B 通过模拟以下步骤完成与
(1) 初始化阶段:给定关键字 w和 参数(p,g,ga,敌手A的交互问题:
(a)初始化一个空的列表HL∈w×G1××{0,1} , PLis ∈×G1;
(b)设置公钥 PK = (p =ga,g,G,GT,︿e);
(c)初始化隐藏关系N,具体实现如下:
随机选择ui←和 Ci←{0,1};
如果Ci= 1,计算P UBi=gb∗ui;
否则,计算P UBi=gui; gb∗u2···gb∗uN), 并将 多 元 组
另N 个隐藏结构构成结合H S E T=(gb∗u1表HL中;
把(P K,PUBi)发送给敌手。
(2) 询问阶段1:
随机预言机查询 OH1(w ):敌手收到关键字w后,进行随机预言机查询,以获取 w的哈希值H(w ),具体执行操作如下:
(b)如果Coin=1,则把
(c)否则,把< w,PUBi,gu1,ui,Ci>加入列表HL,输出gu1。
陷门查询OTrapdoor(w):当敌手自适应地选择随机预言机 OTrapdoor,并获取关键字w ∈{0,1}∗的陷门,B 算法如下:
(a)判断
(b)从列表HL中取出关键字w 的 元组
(3) 挑战阶段:敌手任意选择两个关键词者,随后挑战者执行以下操作生成加密索引:
(c)此时, C0∗,C1∗中至少有一个为0,随机选
(d)将密文Cd∗发送给敌手。
(4) 询问阶段2:这个阶段与查询阶段1类似。但是,不允许询问关键词和 隐藏矢量PU,PU的陷门和索引。b′=b ,算法B 输出1,否则输出0。
(5) 猜测阶段:敌手A输出一个比特 b′。如果
4 分析与实验
4.1 理论分析
将PSEFKS方案与公钥可搜索加密中比较有代表性的Boneh等人的方案[4], Shao等人的方案[15]和隐藏结构的快速公钥可搜索加密(Searchable Publickey Ciphertexts with Hidden Structures,SPCHS)[19]方案进行对比。其中,Boneh等人的方案是最经典的公钥可搜索加密方案,大部分的公钥可搜索加密都是基于本方案的改进,Shao等人的方案是第1个实现可以抵御内部关键字攻击的方案;在文献[19]的SPCHS方案中,采用了快速的倒排索引,以此提高了密文搜索效率。但在确保密文在CSP关键字攻击方面的安全性上,SPCHS方案对于诚实而好奇的云服务器的猜测攻击问题存在不足,云服务器可以通过逐个关键字匹配来获取用户密信息。本文方案不仅实现了快速的并行倒排索引,还实现了抵御内部关键字攻击。另外,对各方案在不同阶段的计算成本进行比较,其中E为运行模指数运算所用时间,H为运行哈希运算时间,P为计算双线性映射所用时间。
如表1所列,将PSEFKS与Boneh等人的方案,Shao等人的方案和SPCHS从生成加密秘钥、生成加密索引、生成关键字陷门和密文搜索4个阶段进行对比。
PSEFKS依赖双线性对运算,在生成公私钥时和Boneh生成密钥算法相同,需要两次模密运算。在进行索引构建时,SPCHS需要两次双线性对运算,但PSEFKS基于SPCHS倒排索引进行改造,只有在查找到匹配关键字时进行1次双线性对和1次哈希运算。在陷门生成时,因为加入了数据拥有者的公钥,所以相比Boneh等人的方案多了1次双线性对运算。最后,在查找阶段因采用并行倒排索引结构,在进行匹配时只需1次哈希和1次双线性映射,即可完成可搜索密文和陷门的匹配工作。Boneh等人,Shao等人的方案都是基于正向索引构建的,在生成关键字密钥时,Boneh与总的生成关键字密文数有关。SPCHS基于倒排索引构建,搜索效率与关键字个数成正比,但需要两个双线性对运算。Shao的运行时间与n的大小线性相关,其中n为关键字的阶。所以,相比Boneh和PSEFKS方案,Shao方案在生成秘钥时,所需时间最长。Setup函数在终端的每次运行理论值为1,因Shao方案在抵御内部关键字攻击方面需要第三方认证机构,所以,在不考虑生成函数运行的时间情况下,Shao的方案约为本方案运行时间的4倍。

表1 性能分析
表2总结了各方案的安全性情况。PSEFKS方案相比Boneh, Shao和SPCHS的方案,通过给数据拥有者分配公私钥,是一个可以抵御内部关键字攻击的方案。另外,在索引构建过程中,我们引用并行的快速倒排索引方式,根据关键字生成密文的次数,记录关键字域密文的关系结构生成检索模式,实现了密文和陷门的不可分辨且相比Shao方案的在抵御外部关键字攻击方面需要身份信息认证和第三方权威机构的认证,本文有更高的安全性与检索效率。
从Boneh第1次提出PEKS方案,到2015年Shao第1次考虑内部关键字攻击问题,在他们所提方案中,由于都基于正向索引,在进行算法匹配,去寻找包含关键字 的密文文档时,所提算法几乎要把所有的加密索引匹配一遍,故搜索阶段的时间复杂度为o (n)。所以,以上对比方案只适用于文档较少的可搜索加密系统,对于文档较多的系统,效率会严重降低。但是,在PSEFKS方案中,由于采用了并行的倒排索引的加密索引结构,云服务器在收到关键字搜索陷门时,允许并行的执行关键字搜索匹配任务,然后找到所有匹配的论文,提高检索效率。因此,在现今大数据存储的云存储中,本文方案能够在有效的倒排索引下实现抵抗内部关键字攻击的功能,使方案更加安全高效。
4.2 实验分析
实验原型系统的开发和测试是基于Ubuntu18.04系统,所依赖的软件库为PBC-0.5.14[20],GMP,Openssl/crypto和Openssl/sha,实验机器的CPU为Intel(R)Core(TM)i5-7500 CPU@3.40 GHz;选取椭圆曲线为Type-A类型,所用参数选取PBC库中给定的参数文件a.param。

表2 安全性对比
因为PSEFKS方案是在SPCHS方案索引的基础上进行改进的,因此增加与SPCHS方案的对比。对比在4个主要方面进行:数据拥有者产生可搜索密文时间、数据用户产生陷门时间、云服务器进行关键字搜索匹配时间和所占空间大小。
图4展示了PSEFKS和SPCHS在进行生成加密索引、生成陷门和搜索性能3个方面的比较。在图4(a)中,SPCHS方案使用链式索引关系,只有在已知前一个密文的基础上根据链式指针查找下一个关键字密文,查找效率相对较低。而在PSEFKS方案中,索引关系允许关键字进行并行搜索。因此,在云服务器获得用户陷门,可以通过本文方案中的Test算法进行比较和遍历。当该索引指向的密文的明文包含关键字 w时,才需要进行一次双线性配对运算。
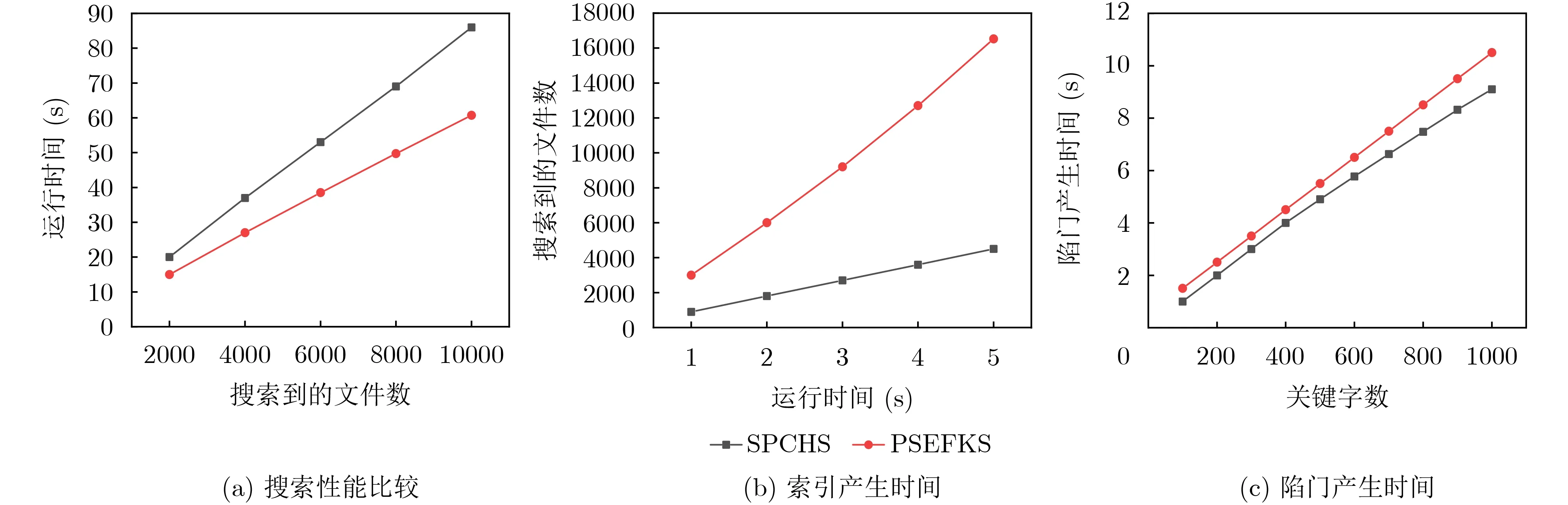
图4 效率比较
图4(b)在进行构建关键字索引时,PSEFKS有一个公共的参数指向头部,加密索引阶段主要包括转换为哈希字符串和映射群元素G的运算。由于PSEFKS在加密关键字索引时,引入计算器操作,相对耗时多一些。但在加密文档数量较多时,在4000个关键字文档后,依然与所加密的关键字密文数成正比。但SPCHS由于需要在链式隐藏索引结构查询插入关键字密文,所以会随着关键字密文数增加而逐渐增大。如图所示,在产生10000个可搜索加密密文时,SPCHS方案大约需要80 s,而本文方案仅仅需要40 s。因此,在生成关键字可搜索的密文时,PSEFKS方案有了很大的改进。
图4(c)展示了在陷门生成时所需时间的方案对比。在SPCHS中,关键字生成需要有两个参数,分别是数据用户的私钥S K和 所需的关键字w ,算法只需1次幂指运算。在本文PSEFKS中,因为需要加入数据用户的公钥 PK,所以,相比SPCHS来说,需要多一次双线性对映射运算。所以,在陷门生成时,PSEFKS方案的效率略低于SPCHS方案。
本实验通过统计评估生成的关键字可搜索密文的字节大小,比较了PSEFKS方案和SPCHS方案的通信成本。在SPCHS方案中,关键词字典中不仅存储了加密关键字信息,还需额外的空间来存储关键字密文之间的关系结构。而在本文PSEFKS方案中,采用隐藏关键字结构的星型倒排索引结构,不需要额外的信息存储密文关系。如图5所示,实验对比表明,10000个关键字可搜索密文,PSEFKS方案约需要350 KB, SPCHS的比较方案约需要3600 KB。因此,通过与SPCHS方案相比,PSEFKS方案的通信成本大大降低。因此,通过与SPCHS方案相比,PSEFKS方案的通信成本大大降低。
综上所述,在SPCHS隐藏关系的链式倒排索引的基础上,本文方案的星型倒排索引,只需关键字经过 H2((H1(w)Kw, pu))计算,生成相应的可搜索加密密文,不仅降低了存储开销,在搜索阶段可进行并行操作,提高了检索效率。而且,在生成关键字索引时,加入数据拥有者的私钥,使本文方案可以抵抗内部关键词攻击。

图5 通信成本比较
5 结束语
本文提出一种快速的可抵御内部关键字攻击的公钥可搜索加密方案。主要贡献为:首先,提出一个高效快速的抵御内部关键字攻击方案PSEFKS,可以抵御云服务器等敌手通过加密索引等关键字实施关键字猜测攻击,从而保障了系统的安全性;其次,通过分析基于倒排索引的隐藏结构关系,改进了加密索引的构造方式,同时结合现有的公钥可搜索加密方案,构建了高效并行的倒排索引,减少了在搜索阶段服务器执行双线性配对运算时间,从而提高了搜索效率。本文方案在使用倒排索引时,无法充分保证对加密数据的动态更新问题,因此后续工作将考虑对倒排索引结构进行改进,在保证用户的搜索效率和安全性的同时,可以对索引结构进行动态更新。
