循环相关熵谱密度估计高效算法研究

李 辉

(天津职业技术师范大学机械工程学院 天津 300222)

1 引言

循环平稳信号处理理论产生于20世纪70年代，并在20世纪90年代得到迅速发展，已经成为一种有效的信号处理方法[1–4]，其研究对象主要是针对非平稳信号中的一类特殊信号——其统计量具有周期性变化特征的非平稳信号，即循环平稳信号。循环平稳信号处理方法引入循环频率，从而在循环频率和谱频率构成的双频图中，很好地描述循环平稳信号的频谱特征，已在通信领域[5–7]、机电设备故障诊断[8,9]等领域得到了广泛应用。传统的循环平稳信号处理理论基于信号的2阶统计量，能够较好地抑制高斯噪声，但在处理非高斯噪声(如Alpha稳定分布噪声)时，会造成性能衰退，甚至失效[10]。近年来，有效处理Alpha稳定分布噪声的信号处理方法，主要有基于分数低阶统计量[11–14](Fractional Lower-Order Statistics, FLOS)方法和基于相关熵[15–17](correntropy) 的方法，而FLOS方法尽管能够有效抑制脉冲噪声的影响，但却过度依赖于对信号噪声Alpha值的先验知识或精确估计，因而限制了FLOS方法的应用[10]。基于相关熵理论的循环相关熵方法是处理脉冲噪声的另一种有效方法，已在雷达和通信信号检测、信号滤波、波达方向估计和时延估计等方面得到应用和验证，取得了良好效果[10]。但在已发表的相关文献[18–21]中，循环相关熵谱密度估计还缺乏高效的估计算法，且循环相关熵谱密度的估计性能还有待进一步提高和改进。

循环平稳信号处理方法的有效应用得益于高效的谱相关密度估计技术。谱相关密度估计常用的方法有循环相关图和循环周期图[22]。为了提高谱相关密度的估计效率和性能，学者们提出了多种估计算法[22–24]。经过几十年的发展，谱相关密度计算方法已日臻成熟[24]。而基于循环相关熵的信号处理方法是最近几年才提出的，循环相关熵谱密度的估计还没有成熟的高效算法，大多采用巴西学者Fontes等人[20]提出的算法，该算法采用循环周期图检测(Cyclic Periodogram Detection, CPD)方法计算循环平稳相关熵谱密度，CPD算法采用多重嵌套循环语句计算循环平稳相关熵谱密度，存在计算效率低且计算方法复杂、占用计算机内存多的缺点，严重制约了循环平稳相关熵谱密度在信号处理领域的推广应用，因此，亟需探寻开发高效率、高频谱分辨率的循环相关熵谱密度估计方法。

本文借鉴WVD时频分析算法，提出了一种Correntrogram循环相关熵谱密度估计方法，该方法不仅提高了循环相关熵谱密度计算速度，而且大大提高了频谱分辨率。本文简要介绍了Correntrogram算法的基本原理，推导了计算公式，给出了计算步骤，用仿真调幅信号对Correntrogram算法进行了分析，并与CPD算法和直接算法进行了对比，验证了Correntrogram算法的高效性和可靠性，证明了该算法具有计算速度快、频谱分辨率高、能量聚集性高的优点。

2 循环相关熵简介

2.1 相关熵

2006年美国佛罗里达大学Principe教授研究团队[25–28]在综合利用再生核和信息理论学习(Information Theoretic Learning, ITL)方法的基础上，首次提出了广义相关函数(Generalized Correlation Function, GCF)的概念，并将该广义相关函数命名为相关熵(correntropy)。

对于任意两个随机变量 X 和 Y ，它们的互相关熵(广义相关函数)可定义为

式中， κσ(·)表示满足Mercer条件的核函数，如高斯核函数等，σ 为核函数的核长。

在实际应用中，通常认为随机过程具有时间遍历性，因此可利用随机变量的时间平均来对其进行估计。对于一组长度为 N 的观测样本{ (xi,yi)}1，互相关熵的无偏估计为

对于随机过程 x(t)，时变自相关熵(a u t o correntopy)可定义为

式中， τ为时间滞后量，κσ(·)可采用高斯核函数，其表达式为

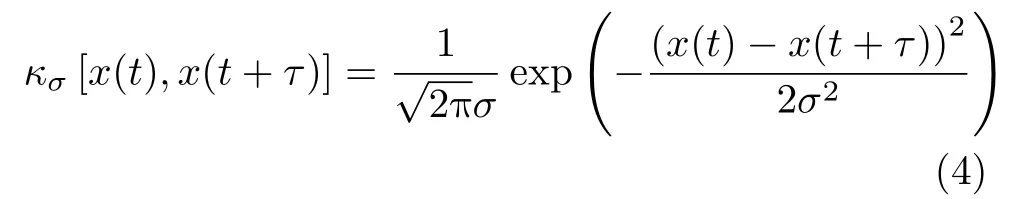
式中，σ 为高斯核函数的核长。

2.2 循环相关熵

2016年，大连理工大学邱天爽教授研究团队[19]将循环平稳信号处理方法和相关熵理论相结合，提出了循环相关熵的概念，给出了循环相关熵函数(Cyclostationary Correntropy Function, CCF)和循环相关熵谱密度(Cyclostationary Correntropy Spectral Density, CCSD)计算公式，并将其成功应用于无线通信信号处理，该方法能从被非高斯噪声污染的信号中提取有用信号的高阶循环平稳特征。

假设时变相关熵 Vxσ(t,τ)具有周期性，且周期为 T0， 对随机过程x (t) 以T0为周期进行采样，则这样的采样值显然满足遍历性，可以用时间平均将相关熵写成

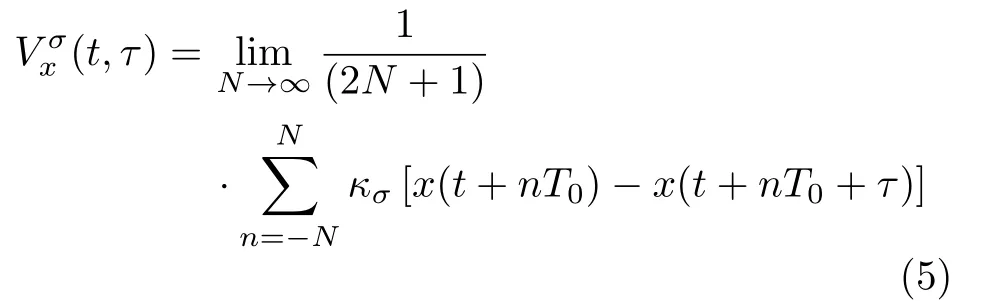
从式(5)可知相关熵 Vxσ(t,τ)是 关于时间t(固定τ)的周期为T0的函数，则有式(6)成立

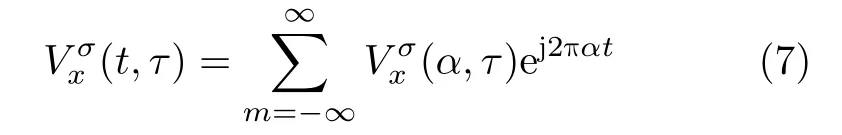
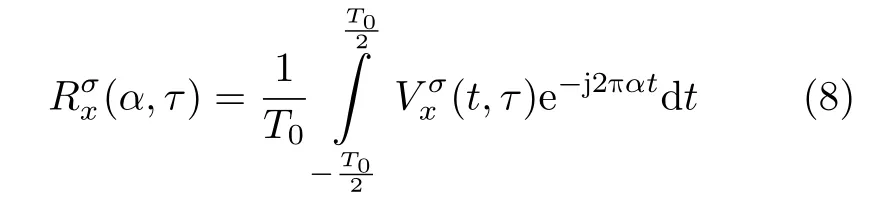
可将式(8)表示为时间平均运算符E [·]形式，即

在式(10)中，当 α =0 时，循环相关熵谱密度退化为传统的功率谱密度。由于循环相关熵函数(α,τ)为广义循环相关函数，因此，循环相关熵谱密度函数(α,f)也称为广义谱相关密度函数。

循环相关熵谱密度函数具有一种特殊的谱相关特性，在频率 f处的循环相关熵谱密度值等于以频率 f 为中心，上下各间隔处的谱分量互相关。利用这种独特的谱相关特性，可以从非平稳的干扰中将特定的循环平稳信号提取出来。

3 循环相关熵估计算法

3.1 CPD算法

2017年，巴西学者Fontes等人[20]提出了CPD方法，并基于CPD算法计算循环相关熵谱密度。CPD算法主要由以下5个步骤组成：

(1) 将信号平均分为 L段，每段采样点数为 N;

(2) 计算每段数据的时变相关熵和信息势；

(3) 计算每段数据的循环自相关熵函数；

(4) 计算循环自相关熵函数的均值；

(5) 计算循环自相关熵谱密度。

CPD算法的实质是采用未重叠分段平均周期图法，主要存在以下4个缺点：(1) 在计算时变相关熵、循环自相关熵函数和循环自相关熵谱密度时，均采用多重循环语句(Fontes等人[20]采用4重嵌套循环语句)计算，计算速度慢，占用计算机内存量大。(2) 在第1步将信号 x分段时，采用非重叠的平均分段方法，即将信号 x 分成互不重叠的 L段，不仅降低了频率分辨率，而且估计的方差也比较大；(3) 在计算时变相关熵和循环自相关熵函数时，未使用任何窗函数，因此，在循环相关熵谱密度图中存在比较严重的“频谱泄漏”，易造成频谱模糊和失真；(4) CPD算法只能计算一种非对称形式的循环相关熵谱密度，不如对称形式的循环相关熵谱密度更直观、频谱结构特征更清晰。上述这些缺点严重制约了循环相关熵谱密度在信号处理领域的推广应用，因此，亟需探寻并开发高效率、高分辨率、更直观的循环相关熵谱密度估计方法。

因相关熵和循环相关熵是最近几年提出的一种信号处理方法，到目前为止，还没有学者发表有关循环相关熵谱密度估计的有效方法方面的文章，因此，本文给出两种计算循环相关熵谱密度的方法，一种是直接利用相关熵和循环相关熵的定义式(4)、式(9)和式(10)进行计算，称为直接算法，另一种是本文提出的Correntrogram算法，以便进行计算效率性能对比。

3.2 直接算法

直接算法是首先根据式(4)和式(9)计算信号的相关熵谱密度函数(α,f)。

3.3 Correntrogram算法

信号x 的瞬时自相关函数Rx(t,τ)定义为

式中， ∗表示共轭运算符。

Wigner-Ville 分布(简称WVD)是典型的二次型变换，它定义为信号 x瞬时自相关函数Rx(t,τ)关于延时τ 的傅里叶变换[29]，即

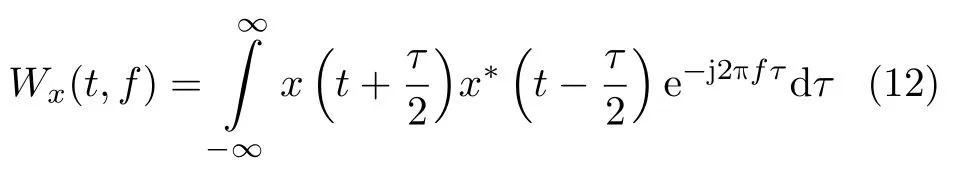
若对x 的瞬时自相关函数Rx(t,τ)关 于时间t 作傅里叶变换，则得到模糊函数，即

式中，T0为 时变相关熵函数Vxσ(t,τ)的周期。

对于实信号x , Vxσ(t,τ)有以下3种形式：

(1) 对称形式

(2) 非对称形式1

(3) 非对称形式2

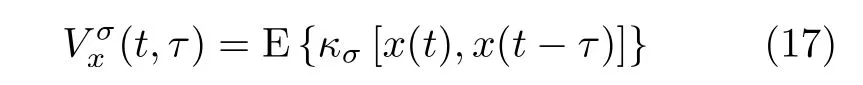
式(15)—式(17)中，κσ(·)为核函数，本文采用高斯核函数。

借鉴功率谱估计中，通过计算信号相关函数的FFT，进行功率谱估计的方法称为相关图(Correlogram)法，因此，将本文通过计算时变相关熵的FFT，进行循环相关熵谱密度估计的算法，称为相关熵图(Correntrogram)算法。

3.4 Correntrogram算法实现步骤

根据2.3节的介绍，可以总结出Correntrogram算法估计循环自相关熵谱密度的步骤：

根据2.3节介绍的基本原理和上述步骤，借鉴时频分析工具WVD实现程序，采用Matlab语言编写了Correntrogram估计循环相关熵谱密度的程序。

4 仿真分析

用一个调幅信号来验证提出算法的有效性和正确性，仿真信号由以下信号成分组成

式中， f0为调制频率，fc为 载波频率，θ 为初始相位。取f0=10 Hz, fc=1024 Hz, θ =0。信号采样频率 fs=6000 Hz，信号采样点数n =2048，通过该仿真信号，验证Correntrogram算法的性能，并与CPD算法和直接算法进行性能对比。

4.1 Correntrogram算法仿真

图1是仿真信号的时域图及其FFT，在图1(a)中能清晰看出调幅信号x (t)的幅值调制特征，在图1(b)中能清晰识别调幅信号x (t)的载波频率和调制频率边频带。运用3.4节提出的信号循环相关熵谱密度估计Correntrogram算法，按式(15)估计调幅信号x(t) 的循环相关熵谱密度(σ =0.1)，如图2、图3和图4所示。图2为循环相关熵谱密度函数的等高线图，图4为其3维图，其双频谱图为对称结构。从图2可以看出，调幅信号x (t)的频谱主要分布在频谱线f =±0.5α 与f =±fc的交点，以及频谱中心(0,0) 和( ±2fc,0), ( 0,±fc)等 位置。调幅信号x (t)的循环相关熵谱在α =±2fc的位置存在明显的谱峰，表明能准确识别载波频率 fc。为了能准确识别调制频率，洞悉循环相关熵谱密度函数的细微频谱结构，图3给出了图2中坐标点( α,f)=(0,0)附近的局部放大图，从图3的中心部分可以看出，该部分为一个菱形频谱区域，在由每相邻4个点组成的小菱形中，小菱形对角线在平行于循环频率轴 α方向的间隔为 2f0，而在平行于谱频率轴f 方向的间隔为f0，这种谱图结构很好地刻画了调幅信号x (t)的调制频率f0， 表明能准确识别调幅信号x (t)的调制频率。

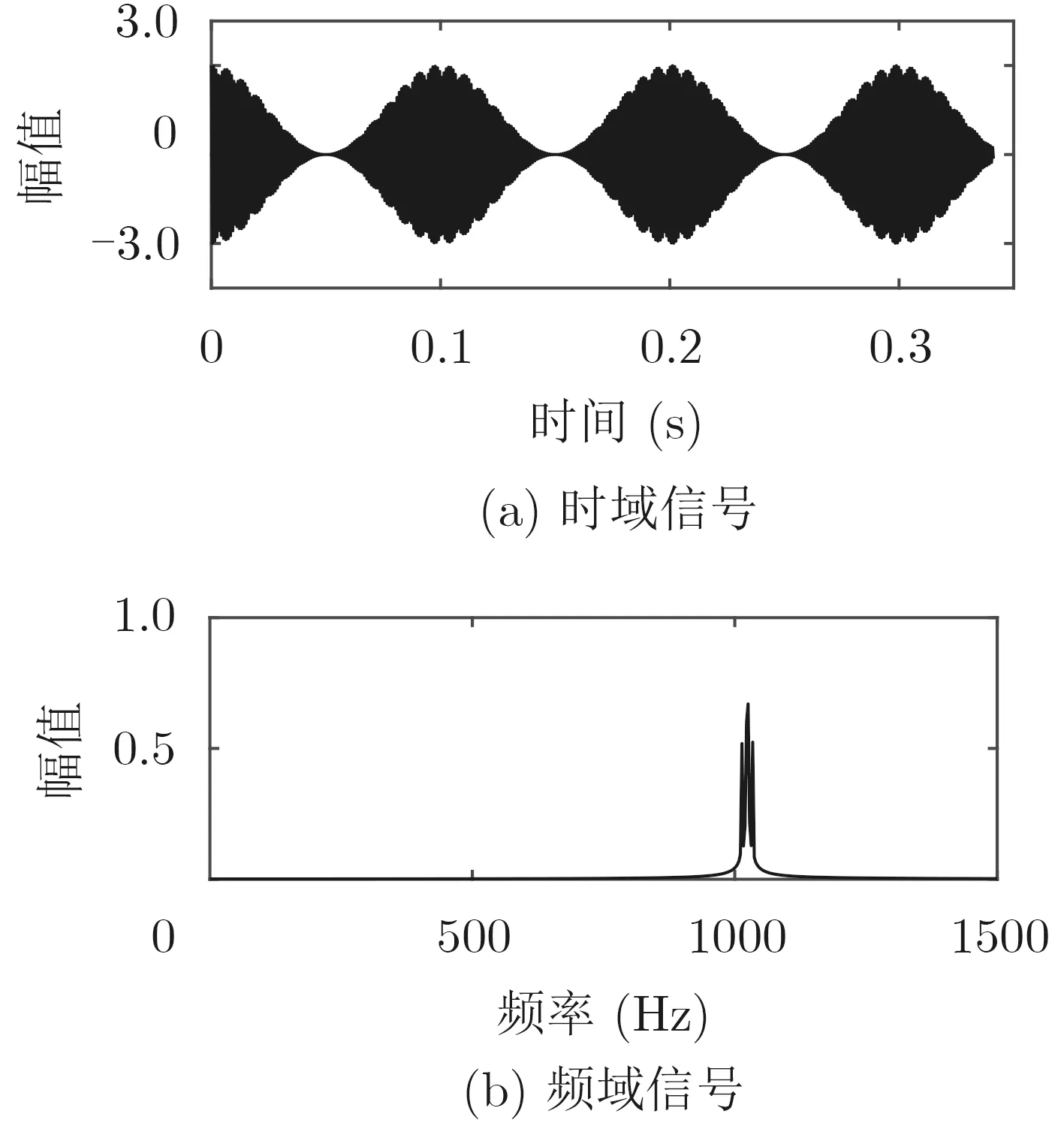
图1 仿真调幅信号

图2 调幅信号循环相关熵谱(Contour图)

图5给出了调幅信号x (t)的广义循环平稳度图，在图5中，在 α=±2fc的位置也存在明显的谱峰，表明能正确识别载频频率fc。图6为图5广义循环平稳度的局部放大图，在循环频率α =0 以 及α=±2fc谱峰两侧，能清晰显示出调制频率边频带。因此，在广义循环平稳度图中，能正确识别调制频率f0。

采用本文算法计算调幅信号循环相关熵谱的运行时间为0.937 s，程序运行参数为：计算机型号intel i7-2600，双核CPU 3.4 GHz，内存3 GB, Windows XP操作系统，使用的软件为Matlab R 2018b。

Correntrogram算法的循环频率 α的分辨率∆α=fs/n ，谱频率f 的分辨率∆ f =fs/n，从图2、图3和图4可以清晰看到，调幅信号x (t)的频谱为相互独立的频谱点，具有很好的频谱分辨率和频谱能量聚集性，能清晰刻画调幅信号的频谱结构特征。另外，Correntrogram算法充分利用了Matlab语言高效的向量和矩阵运算能力，其计算的复杂度为O(n×lg n)(n 为信号的采样点数)，因而Correntrogram算法计算速度很快。

图7和图8为采用CPD方法计算的调幅信号循环相关熵谱，其双频谱图为一种非对称结构，频谱主要分布在 f =0.5α 及( 0,0), ( ±2fc,0) , ( 2fc,2fc)和(−2fc,−2fc)等位置，如图7中点划线绘出的六边形区域。在图7和图8中，调幅信号 x (t)的循环相关熵谱在α =±2fc的位置存在明显的谱峰，表明CPD算法的计算结果能准确识别载波频率。图9给出了图7中坐标点 (α,f)=(0,0)附近的局部放大图，从图9的中心部分可以看出，其频谱线为相互连通的区域，存在比较严重的“频谱泄漏”现象，因而不能有效识别调幅信号 x (t) 的 调制频率f0。在图8中，α=0处的频谱线也连在了一起，说明CPD算法的频谱能量聚集性较差。图10给出了调幅信号x (t)采用CPD算法计算的广义循环平稳度图，在循环频率 α =0 以及α =±2fc谱峰两侧，不能正确显示出调制频率边频带，因此，不能有效识别调制频率f0。

图3 调幅信号循环相关熵谱局部放大图

图4 调幅信号循环相关熵谱3维图

图5 广义循环平稳度

图6 广义循环平稳度(局部放大)

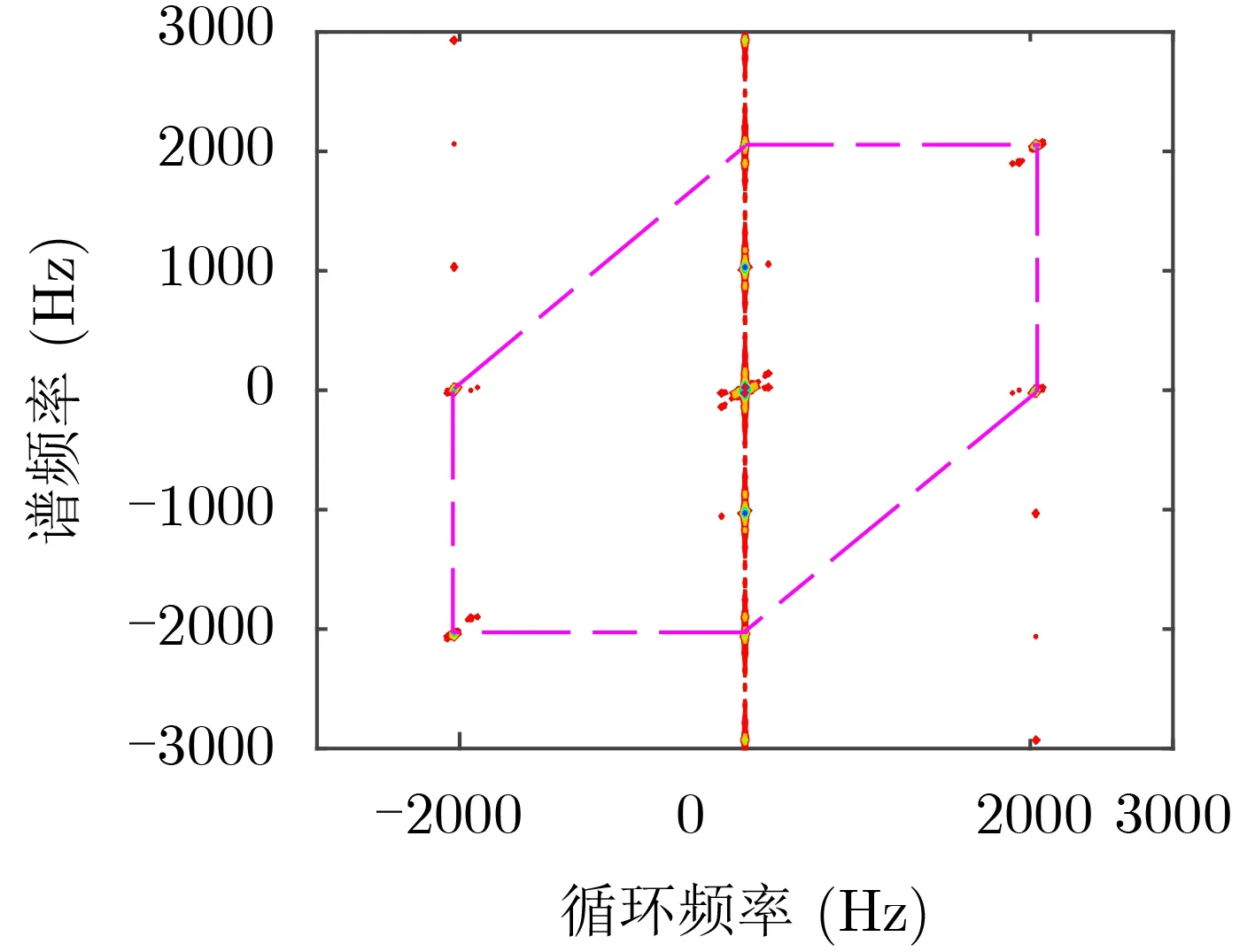
图7 调幅信号循环相关熵谱Contour图(CPD算法)

图8 调幅信号循环相关熵谱3维图(CPD算法)

4.2 CPD算法仿真

为验证本文提出Correntrogram算法的高效性和高频谱分辨率，与Fontes等人[20]提出的CPD算法进行了对比。采用CPD算法计算调幅信号x (t)的循环相关熵谱的运行时间为337.829 s，与Correntrogram算法相比，Correntrogram算法的计算速度比CPD算法快360.5倍。由于CPD算法采用4重循环语句计算谱相关熵密度，因此，其计算的复杂度为O(N4)( N为每小段数据采样点数)，计算效率较低。

对比图2、图4与图7、图8可以看出：Correntrogram算法计算的循环平稳相关熵谱密度，在频谱图中是相互分离的谱峰，循环频率 α的分辨率∆α=fs/n为 2.93 Hz，谱频率f 的分辨率∆f =fs/n为2.93 Hz，频谱分辨率高，无频谱泄漏现象。而CPD方法计算的循环相关熵谱密度，取每小段数据采样点数N =256，在频谱图中是互连的谱峰，存在比较严重的频谱泄漏现象。循环频率 α的分辨率∆α=fs/n为 2.93 Hz，谱频率f 的分辨率∆f =fs/N为23.44 Hz，谱频率分辨率较低；同时，由于在信号分段时未使用任何窗函数，因此，在循环相关熵谱密度图中存在比较严重的“频谱泄漏”现象，导致载波频率 fc的 旁瓣掩盖了调制频率f0的谱峰，造成了频谱模糊和频率失真，因而不能正确识别f0=10 Hz的调制频率。

图9 调幅信号循环相关熵谱(局部放大图)

图10 广义循环平稳度

4.3 直接算法仿真

直接利用相关熵和循环相关熵的定义式(4)、式(9)、式(10)和式(16)对式(18)的仿真信号x (t)进行计算，为便于进行性能对比，直接算法采用与CPD算法相同的频谱分辨率。采用循环频率 α的分辨率 ∆α=fs/n 为2.93 Hz，最大延时τmax=128个数据采样点，谱频率 f的分辨率∆ f =fs/(2τmax)为23.44 Hz。采用直接算法计算调幅信号x (t)的循环相关熵谱的运行时间为174.594 s，与Correntrogram算法相比，Correntrogram算法的计算速度比直接算法快186.3倍，由于直接算法采用双重循环语句计算循环相关熵谱密度，其计算的复杂度为O(n2)( n为信号的采样点数)，计算时间与频谱分辨率∆α 和∆ f 有关，∆ α 和∆ f越小，计算时间越长。

图11和图12为采用直接算法计算的调幅信号循环相关熵谱。从图11和图12可以看出，直接算法计算的频谱结构与CPD算法计算的频谱结构相同，因谱频率f 的分辨率∆ f较低，因此，直接算法计算的调幅信号循环相关熵谱也不能有效识别信号x(t) 的调制频率f0。

图11 调幅信号循环相关熵谱(Contour图)

图12 调幅信号循环相关熵谱3维图(直接算法)

Correntrogram算法不仅能计算式(15)所示的对称形式高斯核的循环相关熵谱，而且也能方便计算式(16)、式(17)所示的非对称形式的循环相关熵谱。图13和图14为根据式(16)计算的非对称形式1高斯核的循环相关熵谱，图15和图16为根据式(17)计算的非对称形式2高斯核的循环相关熵谱。从图13、图14和图15、图16可以看出，非对称形式的循环相关熵谱为非对称结构。为便于与式(15)计算的对称形式高斯核的循环相关熵谱进行对比，图17给出了图13中坐标点 ( α,f)=(0,0)附近的局部放大图，从图17的中心部分可以看出，该部分为一个平行四边形频谱区域，平行于循环频率轴 α方向两个相邻谱峰的间隔为 f0， 而平行于谱频率轴f 方向相邻谱峰的间隔也为f0，这种谱图结构也很好地刻画了调幅信号 x (t) 的调制频率f0。对比图2与图13、图15可知，对称形式的循环相关熵谱图(图2)比非对称形式的循环相关熵谱图(图13和图15)更直观，频谱结构特征更清晰。

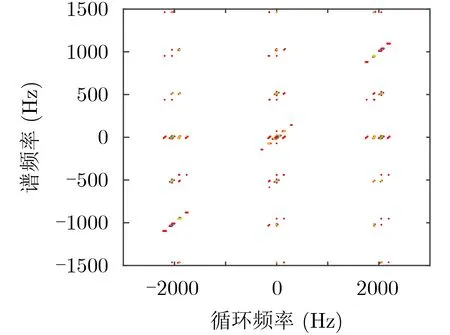
图13 调幅信号循环相关熵谱(非对称1)

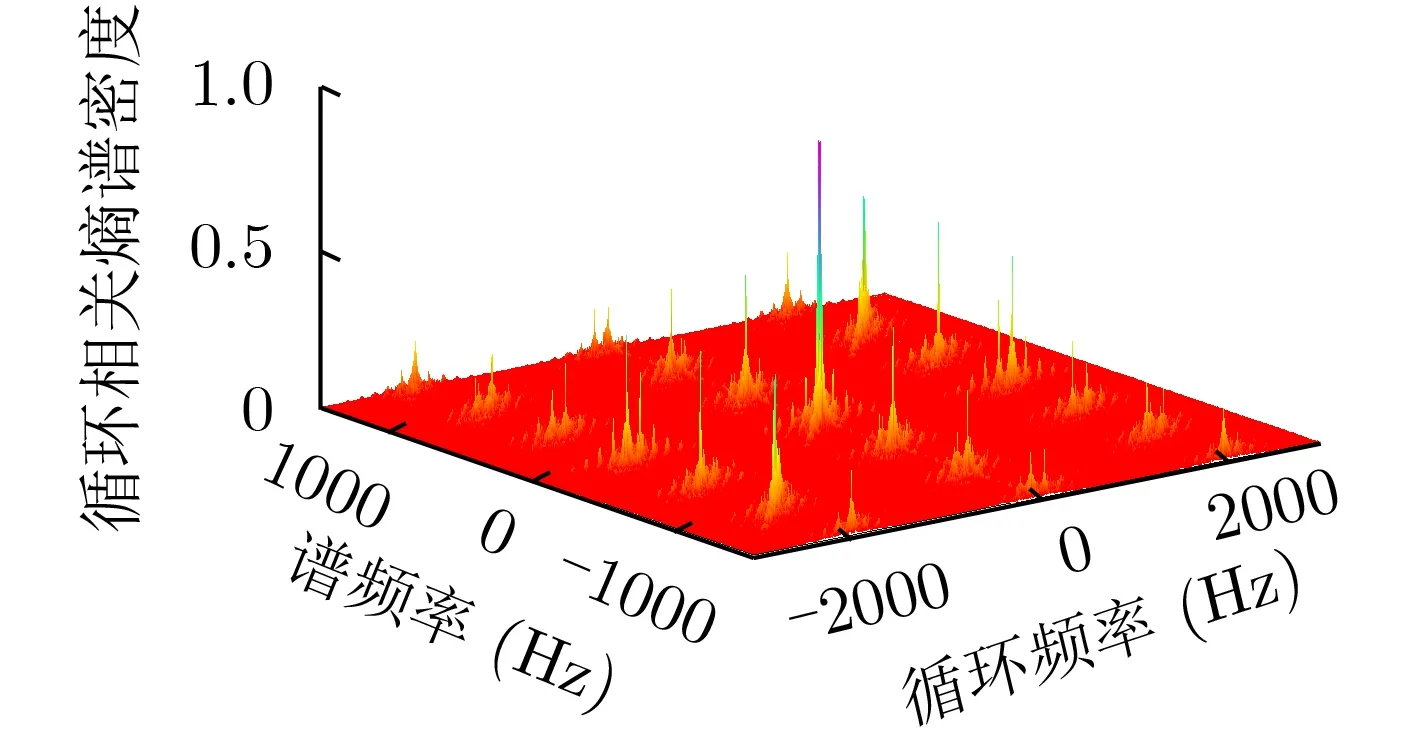
图14 调幅信号循环相关熵谱3维图(非对称1)

图15 调幅信号循环相关熵谱(非对称2)

图16 调幅信号循环相关熵谱3维图(非对称2)

图17 调幅信号循环相关熵谱(非对称1局部放大图)

5 结束语

借鉴Wigner-Ville 分布方法，本文提出了一种循环相关熵谱估计的高效算法—Correntrogram，并与循环周期图检测(CPD)算法和直接算法进行了对比，Correntrogram 算法克服了CPD方法计算效率低、频谱分辨率低和易产生“频谱泄漏”的缺陷。简单介绍了该算法的基本原理和实现步骤，并用Matlab语言编制了算法程序。通过仿真调幅信号验证了Correntrogram算法的性能，Correntrogram算法不仅能提高循环相关熵谱估计的计算速度，而且能有效提高频谱分辨率，消除“频谱泄漏”现象，因此，Correntrogram算法是一种循环相关熵谱估计的高效、可靠算法。