脉冲噪声下一种自适应ASR稳健滤波方法

金 艳 李亚刚 姬红兵

(西安电子科技大学电子工程学院 西安 710071)

1 引言

Alpha稳定分布[1–3]是一类极具吸引力的脉冲信号模型，可以对水声、雷达、地震等探测领域中，遇到的具有显著脉冲性和厚重概率密度函数拖尾的噪声进行很好的描述，其特征指数 α可表征噪声脉冲 特性的强弱， α值越小，则分布的拖尾越厚，出现脉冲异常值的概率越大且其幅值越高，即噪声的脉冲特性越强。但 α稳定分布概率密度函数缺乏统一的解析表达式，在实际应用中受到很大的限制。此外，传统的基于高斯模型的信号处理方法在脉冲噪声下不再适用，已有学者提出分数低阶理论，中值滤波和基于 α稳定分布特例的Myriad[4,5]滤波、Meridian[6]滤波等多种降噪方法，但在强脉冲噪声下性能明显下降。

对此，本文提出ASR(A SαS Robust)滤波方法，该方法基于M估计理论[7]，选取 ASαS(Approximate Symmetric alpha Stable)分布这一具有统一概率密度表达式的脉冲噪声模型，构造适用于脉冲噪声背景的稳健滤波代价函数簇。相比Myriad滤波和Meridian滤波均基于 α稳定分布特例构造的代价函数，本文构造的代价函数簇适用的脉冲噪声范围更广，且可利用代价函数求导所得的影响函数对ASR滤波方法进行性能评估。ASR滤波器选取不同的线性度参数可实现不同的滤波效果，本文在缺乏噪声先验信息的情况下，采用阈值选择法实现线性度参数的自适应选择。此外，从代价函数和影响函数两个方面分析了Myriad滤波和Meridian滤波均服从本文提出的ASR滤波方法。

线性调频(Linear Frequency Modulation, LFM)信号[8]，是一种典型的非平稳信号，在声呐、雷达等技术中有广泛应用。利用短时傅里叶变换[9](Short Time Fourier Transform, STFT)进行时频分析结合Hough变换[10]在时频2维平面搜索，可以完成LFM信号的参数检测与估计。但在强脉冲噪声背景下，上述方法性能严重退化。因此，本文将ASR滤波方法推广到时频2维平面上，提出了可有效抑制脉冲噪声的AS-FT(ASR STFT)方法，利用LFM信号参数估计的结果表明该方法的抑噪性能，研究ASR滤波方法的稳健性。此外，需要说明的是，ASR滤波方法不仅适用于线性调频信号，在脉冲噪声环境下均可适用。

2 M估计原理

基于位置参数的最大似然估计是在M估计[11]基础上发展起来的一类重要的稳健估计理论，其主要原理如下：

(1) 由背景噪声概率密度函数构造适当的代价函数

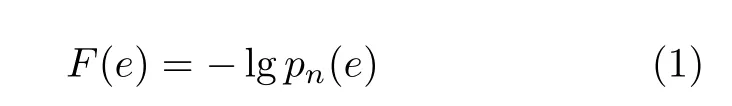
其中，pn(·)是 噪声概率密度函数，e 为误差函数。

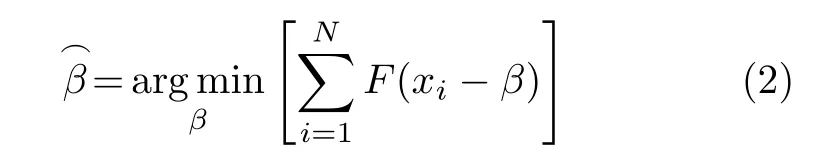
式(2)也可以描述为

其中φ (e)为 影响函数[12]，可由F (e)关 于β 求导所得。

实际上，均值滤波、中值滤波、Myriad滤波和Meridian滤波，就是分别由背景噪声为正态分布、拉普拉斯分布、柯西分布和广乂柯西分布所构造的代价函数得到的。表1为不同滤波器对应的噪声概率密度函数、代价函数和影响函数。

影响函数φ (e)可以描述滤波器输出受异常值的影响程度，因而可用于稳健估计器性能评价。

稳健估计器影响函数的特征有：

(1) B 稳健：若影响函数的绝对值是有界的，即异常值对滤波结果的影响有限，则称该估计器为B稳健。

(2) 抑制点：影响函数中心点到其值为极小时之间的距离称为抑制点[12]，稳健估计器此距离应有限，抑制点可以反映估计器的异常值剔除能力。

如图1所示，均值滤波的影响函数绝对值没有上界，均值滤波显然不是B稳健的，且其抑制点为无穷大，不能剔除异常值；中值滤波、Myriad滤波和Meridian滤波均满足 B稳健条件，但中值滤波的抑制点为无穷大，滤波结果始终受异常值的影响；Myriad滤波和Meridian滤波的抑制点均有限，且影响函数随着异常值的增大而减小。此外，Meridian滤波的影响函数衰减速率比Myriad快，因此Meridian滤波影响函数的抑制点更小，这表明Meridian滤波器比Myriad滤波器异常值剔除能力更强。

3 ASR滤波模型及AS-FT滤波方法

3.1 A SαS 分布

针对对称 α稳定分布不存在统一概率密度函数表达式这一问题，已有学者基于Fourier逆变换法、幂级数展开法和有限高斯混合法等，提出多种近似解析表达式。文献[13]基于脉冲噪声概率分布拖尾的衰减特性，利用PDF和特征函数互为Fourier变换对的关系，采用非线性最小二乘曲线拟合与点匹配方法，提出一种幂级数形式的脉冲噪声分布参数模型，即A SαS分布。

ASαS分布PDF表达式为

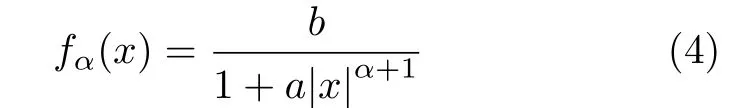
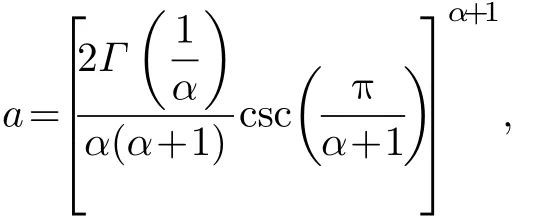
表1 常用滤波器的代价函数与影响函数

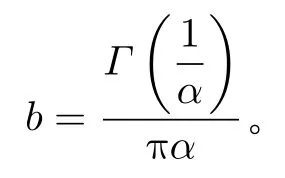
图2为不同特征指数 α所 对应的A SαS分布和对称 α稳定分布的概率密度曲线对比图。如图所示，ASαS分 布与对称α 稳定分布的概率密度曲线相似性较高，当 α较小时，A SαS 分 布与对称α 稳定分布的概率密度曲线较为接近，能很好地反映分布的拖尾情况，且当 α =1.0 时，A SαS 分布与对称α 稳定分布的概率密度曲线拖尾完全重合。上述分析表明，具有统一形式概率密度表达式的 A SαS分布噪声模型是对称 α稳定分布的有效近似，能很好地和实际脉冲噪声数据相吻合。

3.2 ASR滤波模型及其代价函数选取

本文将脉冲噪声建模为A SαS分布，根据式(1)和式(4)得到ASR滤波方法的代价函数簇为

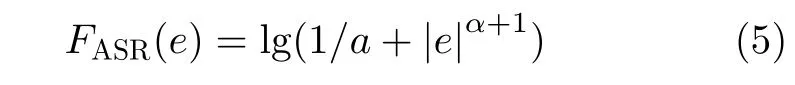
其中，1 /a 为 线性度参数[14]，α 与 A SαS分布特征指数一致，均在区间( 0,2]取 值，α 不同代价函数不同，据此可构造一簇滤波器。

图1 均值滤波，中值滤波，Myriad, Meridian滤波影响函数

图2 A SαS分 布与对称α 稳定分布PDF对比图

稳健估计器的性能可用影响函数来评估，ASR滤波方法的影响函数簇为

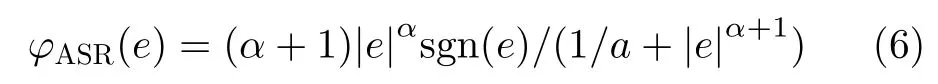
图3为ASR滤波方法影响函数簇中不同α 对应的影响函数，对比稳健估计器影响函数的特征，可得出以下结论。

结论1：ASR滤波方法的影响函数簇中不同α 对应的影响函数都为 B稳健，且满足抑制点条件。这表明ASR滤波方法的代价函数簇是稳健的，据此可建立一簇稳健滤波器。

结论2：α 越小时，其对应的影响函数曲线的衰减率越高，抑制点越小，滤波器对异常值更稳健。

没过多久，因为换工作，我有几个月没事干，真可以到乡间小住一阵。朋友把钥匙拿来，让我一个人在那儿修养身心，说是“换换脑子”。虽没有湖，住的也不是木屋，但确实幽静，也有大片的草地。不怎么有蛐蛐，但能听到远处村子里的狗叫。每天，我都散步到几百米外的小卖部买点吃的喝的，然后端着易拉罐啤酒坐在院子里听狗叫。按理说，这是内省的好时机，离开红尘的喧嚣，擦拭心灵上的灰尘，倾听自己内心的声音。我安静地坐在那里，听到自己内心的声音却是：“要是能上网该多好呀！”

ASR滤波方法参数 α =1时，其代价函数簇和影响函数簇取值分别为

对比表1可知，ASR滤波器参数 α=1时即为Myriad滤波器。

ASR滤波方法参数 α =0时，其代价函数簇和影响函数簇取值分别为

对比表1可知，ASR滤波器参数 α=0时即为Meridian滤波器。

由代价函数和影响函数可知，Myriad滤波和Meridian滤波服从本文提出的ASR滤波方法。本文选取的A SαS 分 布噪声模型，解决了采用α 稳定分布模型缺乏统一概率密度表达式的问题，可对不同强度的脉冲噪声进行模拟，因此ASR滤波方法可以将上述滤波器统一起来，构建稳健滤波的统一框架。

由结论2可知，当α 越小时，其对应的影响函数曲线衰减率越高，抑制点越小，滤波器更稳健。因此，为解决中值滤波，Myriad滤波等在强脉冲噪声环境下性能下降的问题，可从代价函数簇中选取α较小的代价函数，如α =0.5时的代价函数。

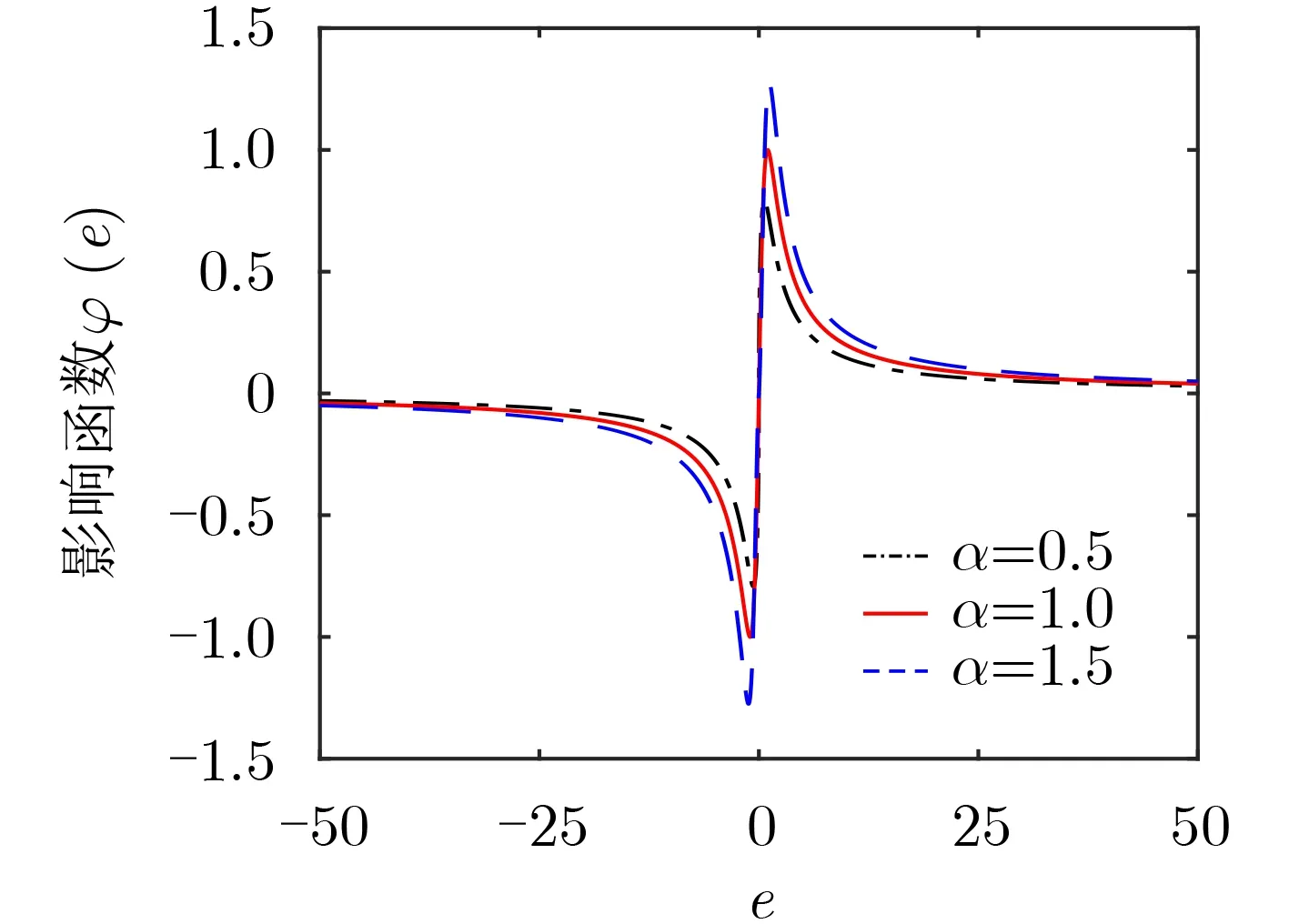
图3 影响函数簇

3.3 线性度参数阈值选择

1/a是 线性度参数，文献[15]指出滤波器异常值剔除能力与线性度参数的选取有关，式(11)给出了1/a的表达式。

由式(11)可知，ASR方法中线性度参数 1 /a的选取与A SαS 分 布的特征指数α 相关，对于不同强度的噪声，可根据式(11)确定线性度参数的取值以使滤波器具有最优的异常值剔除能力。因此，将式(11)中取值与α 对 应的 1/a称为最优线性度参数。

图4和图5分别为A SαS 分 布下线性度参数1 /a随特征指数 α变化的曲线图和PCK均值图。显然，最优线性度参数的获取，需要知道噪声先验信息，即特征指数α 的值。

因此，本文在缺乏噪声先验信息的情况下，为实现线性度参数的自适应选取，提出如下阈值选择方案

其中， ψ0为门限值，PCK(Percentile Coefficient of Kurtosis)为峰度系数百分数，由文献[16]引入用于测量脉冲噪声PDF的拖尾厚度，脉冲噪声PDF拖尾厚度越大，脉冲特性越强。文献[17]借助PCK提出一种阈值选择(switching scheme)滤波机制。

图4 A SαS分布最优线性参数曲线图

图5 A SαS分布下PCK均值图

由2.1节知，A SαS分布可看作具有统一形式概率密度表达式的对称 α稳定分布，因此本文用实测对称α 稳定分布下的PCK均值图作为A SαS分布下的PCK均值图。 A SαS 分布的PCK随其特征指数α 的减小呈减小趋势。借助此性质，本文选取PCK作为自适应参数，以实现在缺乏噪声先验信息的情况下对线性度参数的合理选取。图5中 α=1对应的PCK ≈0.2 ， 选取ψ0=0.2作为门限值，将特征指数划分为α ≥1和 α <1两部分，实现不同强度脉冲噪声的划分。

根据图5中A SαS分布下PCK随特征指数的变化曲线，与图4中最优线性度参数随特征指数的变化关系知，当特征指数α ≥1即 P CK ≥ψ0，可取线性度参数1 /a2=1.9901， 即α =1.5时的最优线性度参数；当特征指数 α <1即P CK<ψ0，可取线性度参数1/a1=0.1851， 即α =0.5时的最优线性度参数。

综上，阈值选择步骤可总结如下：

步骤 1 计算观测信号的PCK

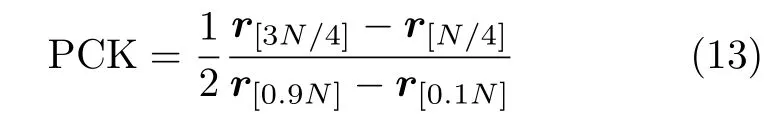
{ri|1} 为 观测 样本{ xi|1} 的 排 序 值ri≤ri+1，式中[ ·]表示取最近的整数值。

步骤 2 利用步骤1所得PCK选取线性度参数

3.4 AS-FT方法

将M估计推广到STFT，则时频平面上某点(n,k)所对应STFT的M估计可由式(2)得

其中，γ (n,k,l)=x(n+l)exp(−j2πlk/N)。

将A S R 滤波方法的损失函数簇FASR(e)=lg(1/a+|e|α+1)代入式(15)求导，再由式(3)，可得隐式方程

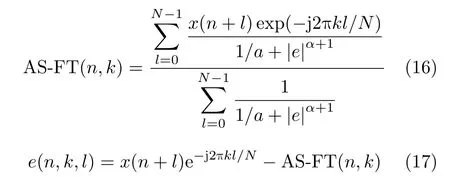
可用不动点迭代算法求解此方程，其步骤为

步骤 1 初始化：令 i=0，将含噪信号的STFT作为迭代初始值，记作S TFT(n,k)，即

步骤 2 计算第i次 迭代值

步骤 3 停止迭代

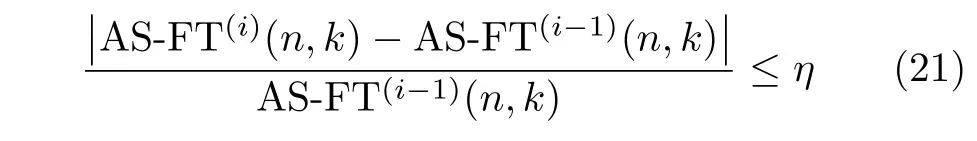
η为迭代停止门限值。

4 仿真实验及分析

LFM信号的数学模型定义如下

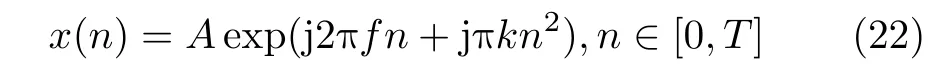
其中，A ,f,k依次为信号的幅值、初始频率和调频斜率， T为信号时宽。本文仿真采用的LFM信号参数为：采样频率fs=1024 Hz， 初始频率f0=50 Hz，调频斜率 k =100 Hz/s， 采样点数N =1024。 ASαS可看作具有统一形式概率密度表达式的对称 α稳定分布，因此本文利用对称 α稳定产生仿真的噪声数据。但α 稳定分布不存在有限的2阶矩，常规信噪比SNR=10 lg(/)中 噪声方差失去意义，因此定义广义信噪比为

依照前文分析，选取ASR滤波方法代价函数簇中α =0.5时的代价函数，利用阈值选择法选取线性度参数，采用AS-FT方法进行滤波，并将AS-FT方法分别与基于Myriad滤波的STFT(MY-FT)，基于中值滤波的STFT(ME-FT)，分数低阶STFT(FL-FT)方法进行对比。

图6(a)为LFM信号的STFT时频分布图，由图可见LFM信号在时频域呈清晰的直线。图6(b)—图6(e)为特征指数α =0.8, G SNR=3 dB 的对称α 稳定分布噪声下，对含噪信号采用不同方法时域滤波后进行STFT得到的时频分布图。图6(b)为含噪信号直接进行STFT的时频分布图，LFM信号的时频特性完全被脉冲噪声淹没，STFT方法在强脉冲噪声的影响下，已经完全失效；图6(c)和图6(d)分别为含噪信号在ME-FT和MY-FT方法下的时频分布图，可以看出ME-FT和MY-FT方法在强脉冲噪声下滤波效果并不理想；从图6(e)可知FL-FT方法相对ME-FT和MY-FT抑制噪声的能力强，但时频平面仍有噪声残留；图6(f)为含噪信号在AS-FT方法下的时频分布图，与LFM信号在STFT方法下的时频分布图对比可知，AS-FT方法具有良好的脉冲噪声抑制效果。

图6 各种方法下时频分布图

本文采用归一化均方根误差(Normalized Root Mean Square Error, NRMSE)来进一步分析脉冲噪声下不同去噪方法的性能，经过100次蒙特卡罗实验，仿真结果如图7所示。

图7 α= 0.8 LFM信号参数归一化均方误差图

由图7可知，当α =0.8时，在强脉冲噪声背景下，STFT方法完全失效，不能实现有效的参数估计；ME-FT方法和MY-FT方法，在GSNR=5 dB时仍不能实现脉冲噪声的抑制；FL-FT在GSNR ≥4 dB时可实现LFM信号的初始频率和调频斜率的准确估计；AS-FT在 G SNR ≥−3 dB时便可准确估计LFM信号的初始频率和调频斜率。在上述脉冲噪声背景下，STFT方法、ME-FT方法和MY-FT方法均不能实现LFM信号参数的有效估计；FL-FT方法和AS-FT方法的LFM信号参数估计性能随着广义信噪比的减小而降低，但与AS-FT方法相比FL-FT方法可以实现更低广义信噪比下LFM信号参数的有效估计。

5 结论

Alpha稳定分布缺乏统一的概率密度表达式，致使传统的基于alpha稳定分布特例的滤波方法脉冲抑制能力有限，为此本文详细比较了 A SαS分布和对称alpha分布的概率密度函数曲线和拖尾特性，采用A SαS分布作为噪声模型，解决了alpha稳定分布缺乏统一概率密度表达式的问题，且实现了不同强度脉冲噪声的模拟。在此基础上，提出ASR滤波方法，构建了稳健滤波的统一框架。理论分析和仿真结果表明，ASR自适应稳健滤波方法与Myriad滤波、中值滤波、分数低阶等稳健滤波方法相比，能实现不同脉冲强度下的噪声抑制。