基于新型阵列的双基地电磁矢量传感器MIMO雷达高分辨角度参数估计

谢前朋 潘小义 陈吉源 肖顺平

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室 长沙 410073)

1 引言

MIMO雷达角度参数估计是当前研究的热点与难点。相比于相控阵雷达，MIMO雷达通过利用相互正交的波形特性可以实现更高的角度分辨率、更大的阵列自由度以及灵活的发射波形设计。由于空间多样性和波形多样性，MIMO雷达可分为分布式MIMO雷达和集中式MIMO雷达[1,2]。进一步地，根据发射阵列和接收阵列的距离，集中式MIMO雷达可以分为单基地MIMO雷达和双基地MIMO雷达。本文主要研究双基地电磁矢量传感器(ElectroMagnetic Vector Sensors, EMVS) MIMO雷达中的角度参数估计问题。

近年来，为了实现双基地MIMO雷达中DOD和DOA的联合参数估计，在文献[3–16]中许多优良的算法被提出。尽管以上所提出的各种算法能够实现双基地MIMO雷达在不同背景下的目标参数精确定位，但是以上各种算法所使用的发射阵列和接收阵列均是标量的均匀阵列或非均匀阵列。相比于标量阵列，电磁矢量传感器阵列不仅能够提供目标的角度信息，同时能够提供目标的极化信息。因此，电磁矢量传感器阵列具有较高的目标分辨率和参数估计能力、稳健的目标检测能力和较强的干扰抑制能力。为了实现双基地EMVS-MIMO雷达的角度参数估计，文献[17]首先提出ESPRIT-Like算法。但是，ESPRIT-Like算法由于需要对接收数据协方差矩阵进行奇异值分解，具有较高的计算代价。为了降低矩阵奇异值分解的计算复杂度，文献[18]利用传播算子(Propagator Method, PM)来实现对接收数据信号子空间的近似。为了利用EMVS-MIMO雷达阵列接收数据的多维张量结构，文献[19]提出协方差矩阵高阶奇异值分解算法来实现对2DDOD和2D-DOA的角度参数联合估计。以上3 种算法针对双基地EMVS-MIMO雷达进行角度参数估计时，面临的问题在于为了实现发射俯仰角和接收俯仰角的角度参数配对，都需要进行构建额外的谱峰搜索类配对优化函数。而且，在进行对发射俯仰角和接收俯仰角求解时，需要从得到的信号子空间中选择合适的参数来构建旋转不变关系。如果参数选择不正确，最终估计得到的角度信息和极化信息将会产生较大的误差。为了避免2D-DOD和2D-DOA的参数配对过程，文献[20,21]分别提出改进的PM算法和PARAFAC算法。但是，文献[17–21]所提出的算法均是基于均匀线性阵列，相应的角度参数估计精度需要进一步提升。因此，为了避免以上算法所面临的问题，本文通过设计新型的发射电磁矢量传感器阵列和新型的接收电磁矢量传感器阵列来实现对双基地EMVS-MIMO雷达的角度参数和极化参数的估计性能的提升。并且，为了避免参数求解过程中，发射俯仰角和接收俯仰角面临的角度参数配对问题，本文提出利用平行因子算法来实现对发射导向矢量矩阵和接收导向矢量矩阵的估计。通过多次迭代之后得到的发射导向矢量矩阵和接收导向矢量矩阵具有自动的参数配对特性。同时，所提出的平行因子算法也充分利用了双基地EMVSMIMO雷达阵列接收数据的多维特性。相比于当前算法，所提算法在保证2D-DOD和2D-DOA角度参数估计精度提升的同时具有较低的计算复杂度。仿真结果验证了所提算法的有效性和优越性。

2 信号模型

如图1所示，考虑一个包含 M个 EMVS 发射阵列和 N个EMVS 接收阵列的新型双基地 EMVSMIMO 雷达系统，其中设计的新型发射阵列和新型接收阵列均包含 2个子阵。对于EMVS发射阵列，第1 个子阵和第2 个子阵均包含M /2个半波长的均匀线性阵列。且第 1个子阵和第2 个子阵的阵元间距为Dt(Dt≫λ/2 )。对于EMVS接收阵列，第1 个子阵和第 2个子阵均包含N /2个半波长的均匀线性阵列。相应的第 1个子阵和第2 个子阵的阵元间距为Dr(Dr≫λ/2)。因此，所设计的新型EMVS发射阵列和新型EMVS接收阵列的阵元位置可以表示为

图1 新型阵列 EMVS-MIMO 雷达系统

假设入射目标个数为 K ，则第k 个目标对应的发射EMVS导向矢量和接收EMVS导向矢量可以表示为

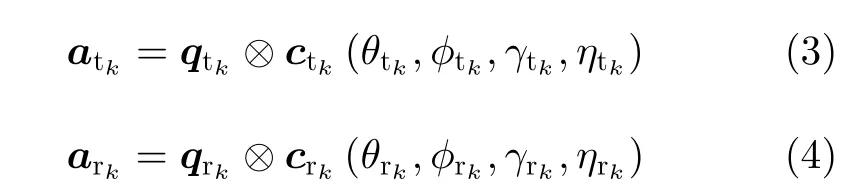
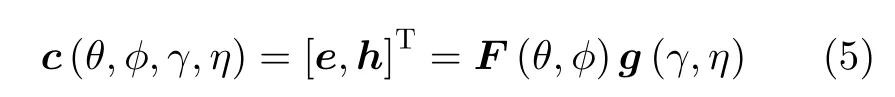
其中，e =[ex,ey,ez]表 示电场域信息，h=[hx,hy,hz]表示磁场域信息。 F (θ,ϕ)∈C6×2表示空间角度位置矩阵，且θ ∈[0,π)表 示俯仰角，ϕ ∈[0,2π)表示方位角。 g(γ,η)∈C2×1表示极化状态矢量，且γ ∈[0,π/2) 表示极化角，η ∈[−π,π)表示极化相位差。

经过以上对电磁矢量传感器空间响应的分析，双基地EMVS-MIMO雷达的阵列接收数据可以表示为

其中， At=Qt⊙Ct=[at1,at2,···,atK]表示发射导向矢量矩阵， Ar=Qr⊙Cr=[ar1,ar2,···,arK]表示接收导向矢量矩阵， n(t)表示加性高斯白噪声矢量。对于 L个采样快拍，总的EMVS阵列接收数据可以被表示为

在文献[17]和文献[18]中直接利用最大似然估计对阵列接收数据进行协方差矩阵的求解，这种处理方法未考虑EMVS阵列接收数据的多维结构特性。根据文献[19]中的分析，双基地EMVS-MIMO雷达的阵列接收数据具有多维张量结构。因此，为了充分利用发射EMVS阵列、接收EMVS阵列和采样快拍之间的内在联系，本文采用3 阶张量模型来处理阵列接收数据的空时特性。

3 基于平行因子算法的高分辨角度参数估计

3.1 角度参数和极化参数联合估计

根据平行因子分解的定义[22]，可以看出式(7)中的双基地EMVS-MIMO雷达阵列接收数据模型可以利用平行因子分解算法进行相应的求解。因此，式(7)中的信号模型可以进一步被表示为

平行因子算法的原理在于，通过多次最小二乘迭代来实现对加载矩阵 At, Ar和S 的求解。如对于已知的 Y ,和，利用最小二乘算法来实现对信号矩阵的求解；对于已知的Yt,和，利用最小二乘算法来实现对发射导向矢量矩阵的求解；对于已知的 Yr,和，利用最小二乘算法来实现对接收导向矢量矩阵的求解。经过对以上迭代过程进行多次的求解，最终能够得到估计性能良好的加载矩阵,和。通过以上的迭代过程得到的和存在一一对应关系，这种对应关系是由于平行因子算法固有的特性。因此，和中的一一对应关系意味着包含在和中的发射俯仰角、发射方位角和接收俯仰角、接收方位角是自动参数配对的。故本文所提算法相比于文献[17–19]中的算法能够避免额外的角度参数配对过程。首先，为了实现对发射角度参数和极化参数进行求解，针对估计得到的发射导向矢量矩阵，定义如下两组对应于粗估计和精估计的选择矩阵

由于设计的新型EMVS发射阵列中两个子阵之间的阵元间距 Dt远大于半个波长，因此，式(16)求得的发射俯仰角是高精度周期模糊的。根据模糊周期与Dt之间的关系，可以得到针对发射俯仰角的所有的高精度周期模糊值为

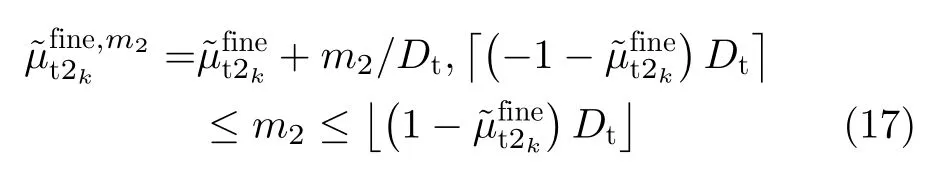
进一步地，为了实现对高精度的发射俯仰角进行解模糊处理，本文利用粗估计的俯仰角作为参考，寻找满足式(18)的约束条件的m2

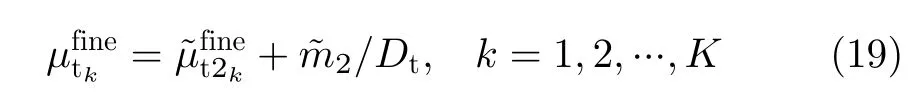
因此，最终的发射俯仰角估计值为

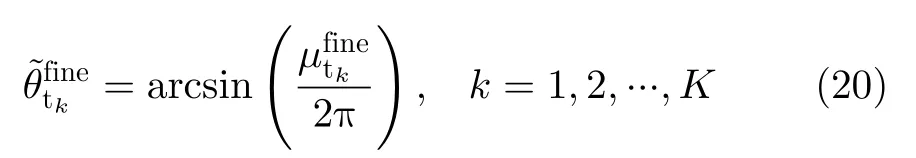
经过以上的精粗估计结合，我们可以得到高精度的无模糊发射俯仰角估计值。从而，相应的发射方位角、发射极化角和极化相位差可以通过矢量叉积算法来进行求解。因此，对于平行因子估计得到的加载矩阵t, E M V S 发射阵列的空间响应(θt,ϕt,γt,ηt)可以通过式(21)得到

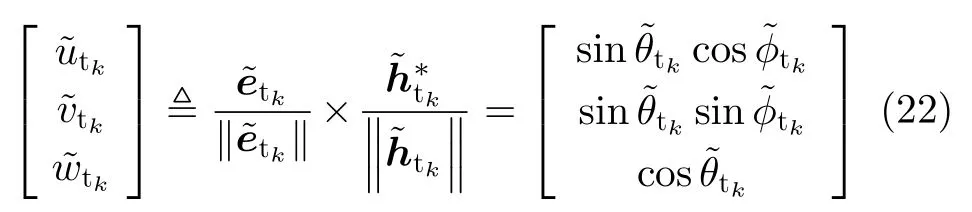
相应的发射极化角和极化相位差可以通过式(24)得到

因此，EMVS发射阵列的极化参数可以表示为

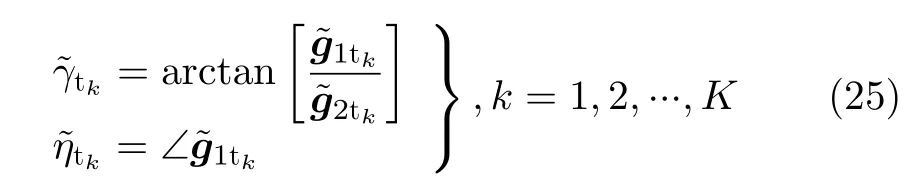
最终，经过以上的处理过程，相应的发射俯仰角、发射方位角、发射极化角和发射极化相位差能够实现精确的估计。并且，以上所得到的关于EMVS发射阵列的 4个参数满足自动配对特性。同样地，对于接收俯仰角、接收方位角、接收极化角和接收极化相位差的估计也能够通过以上的处理过程得到。因此，在本文中，针对估计得到的接收导向矢量矩阵的处理过程进行了省略。

3.2 计算复杂度分析

4 仿真实验

为了验证所提算法的高分辨性能，下面通过仿真实验来验证所提算法与文献[17]中提出的ESPRIT-Like算法，文献[18]中的PM-Like算法和文献[19]中Tensor子空间算法的性能对比。如图1所示，假设EMVS发射阵列个数M =10，EMVS接收阵列个数N =10。且对于EMVS发射阵列和EMVS接收阵列的第 1个子阵和第2 个子阵的阵元个数均为5 。 第1 个 EMVS发射子阵和第2 个EMVS发射子阵的阵元间距 Dt设 置为5 λ ，第1 个EMVS接收子阵和第 2个EMVS接收子阵的阵元间距Dr设 置为6 λ。假设入射的窄带非相关目标的个数 K =3，且入射信源的4维参数和文献[17]中的仿真参数一致。

实验1角度参数自动配对特性

在这个仿真实验中，我们利用星座图来验证所提算法的角度参数自动配对特性的有效性。在实验中，快拍数 L为200，信噪比设置为10 dB，图2中的星座图是通过100次蒙特卡洛仿真实验得到的仿真结果。从图2中可以看出，所提出的算法在保证估计精度的同时能够实现发射俯仰角和接收俯仰角、发射方位角和接收方位角的角度参数自动配对。

实验2算法估计性能随信噪比的变化

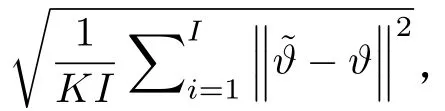
5 结束语

本文的主要贡献在于通过对双基地EMVS-MIMO雷达的发射阵列和接收阵列的设计来实现角度参数和极化参数估计性能的提升。通过对EMVS发射阵列和EMVS接收阵列进行设计，高精度的发射角度参数和接收角度参数可以利用构建的精粗估计结合来实现。并且，通过使用平行因子算法能够实现发射角度参数和接收角度参数的自动配对，从而避免额外的角度参数配对过程。同时，通过归一化坡印亭矢量得到的方位角、极化角、极化相位差和俯仰角也是自动参数配对的。相比于当前算法，由于所提出的平行因子算法不需要进行阵列接收数据协方差矩阵的奇异值分解过程，因此所提算法在保证估计精度提升的同时进一步降低了算法的计算复杂度。仿真实验表明，本文所提出的算法具有优良的参数估计性能。

图2 所提算法角度参数估计星座图

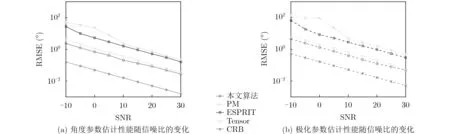
图3 信噪比对算法的影响