模块化多电平换流器型多端高压直流输电控制参数优化方法
2021-03-17刘宛菘秦博宇张若微刘佳玲
刘宛菘,秦博宇,张若微,刘佳玲
(1.西安交通大学 电力设备电气绝缘国家重点实验室,西安 710049;2.西安交通大学 陕西省智能电网重点实验室,西安 710049;3.西安交通大学 电气工程学院,西安 710049)
0 引 言
基于模块化多电平换流器的高压直流(modular multilevel converter based high voltage direct current, MMC-HVDC)输电系统具有无换相失败问题、较低的开关频率、接近正弦的输出波形、适用于整合不同类型能源等优点,目前已经广泛应用于输电领域[1-2]。MMC-HVDC系统能够在不改变电压极性的情况下改变潮流方向,为组成多端直流(multi-terminal direct current, MTDC)输电系统提供了可能,有效提高了电力系统供电可靠性[2-3]。近年来,在全球范围内已有多个模块化多电平换流器型多端直流(modular multilevel converter-based multi-terminal direct current, MMC-MTDC)工程在建或投产,如美国跨湾工程、浙江舟山五端直流输电工程、张北四端直流输电工程等[4]。因此,基于MMC的多端直流输电系统已成为未来智能电网和全球能源互联发展的重要趋势[5]。
目前,已有研究分析了MMC-HVDC系统的小干扰稳定性[6-13]。文献[7]采用阻抗法对MMC-HVDC与风电场互联系统的稳定裕度进行了预测。特征值分析法也被用于研究单端MMC[8]、背靠背MMC-HVDC[9]和MMC-MTDC[10]的小干扰稳定性。文献[10]与文献[12]采用平均值模型分别分析了MMC-HVDC和MMC-MTDC的阻尼特性和动态响应。文献[8]和文献[13]采用考虑MMC换流站内部谐波动态的详细模型,分别分析了在平衡和非平衡电网条件下,控制系统对单端MMC的小干扰稳定性的影响。上述研究结果表明,控制系统密切影响MMC-HVDC系统的稳定性。
MMC控制系统采用d-q解耦控制策略以控制换流站的功率或电压,通常通过比例-积分(proportional-integral,PI)控制器实现。为增强系统的稳定性,需要合理地设置PI控制器的参数。控制参数优化已经在风电场并网HVDC[6]、双馈异步风力发电机组[14]、微电网群[15]、磁悬浮轴承转子系统[16]等领域得到了广泛的应用。MMC-MTDC控制系统间相互作用复杂,控制参数较多,采用传统的试错法对多个控制参数协同优化十分困难,且控制参数优化问题是一个受特征值约束的非线性问题[15]。因此,已有研究采用了启发式算法对其进行求解,如粒子群优化算法[17-18]、遗传算法[16,19]、人工鱼群算法[20]等。然而,启发式算法在优化过程中缺乏明确的搜索方向,迭代次数较多,耗时较长。
参数灵敏度能够反映参数变化时,系统特征值的变化方向和幅度,因此可为控制参数的设置提供指导。基于参数灵敏度提出了一种MMC-MTDC系统控制参数的优化设计方法以提高系统的稳定性。首先,建立MMC-MTDC系统的小信号模型;其次,建立以特征值为目标函数的控制参数优化问题;然后,提出一种基于参数灵敏度的优化算法对优化问题进行求解,并采用回溯直线搜索(backtracking line search, BLS)确定每次迭代的搜索步长,防止迭代振荡,提高收敛速度。由于优化方向和步长取决于控制参数的灵敏度,因此每次迭代的结果都能单调地提高系统的稳定性。然后,在一个三端MMC-MTDC输电系统中应用所提出的控制参数优化方法,在不同扰动下测试其动态性能,并与粒子群算法进行比较,验证所提方法的有效性。
首先建立了MMC-MTDC输电系统的状态空间模型,并对其在某一稳定工作点附近线性化,获得MMC-MTDC系统的小信号模型。
1.1 MMC-MTDC系统的状态空间模型
基于文献[8]与文献[13],MMC-MTDC系统的状态空间模型包括MMC主回路、MMC控制系统、交流系统、直流系统,各部分结构如图1所示。
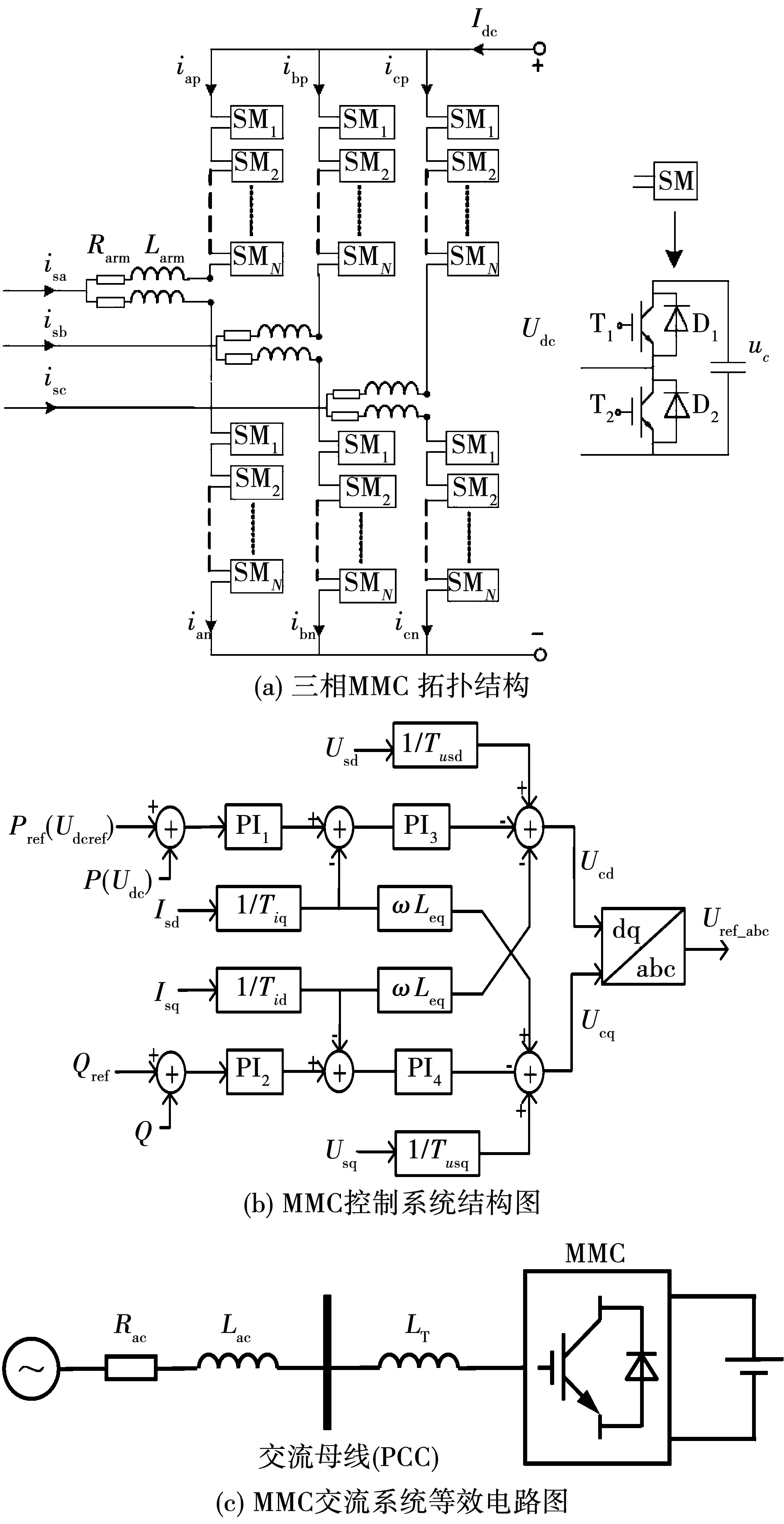
图1 MMC-MTDC各部分结构图Fig.1 Structure of each part in MMC-MTDC system
对于MMC主回路,采用平均值模型[8]进行建模,得到其在d-q坐标系下的状态空间模型为:
(1)
式中:Isd、Isq分别为交流系统d轴、q轴电流;Usd、Usq分别为交流系统d轴、q轴电压;Ucd、Ucq为经d-q变换后的三相基频参考电压;Rarm、Larm分别为桥臂的等效电阻和等效电感;Req=RT/2+Rarm,Leq=LT/2+Larm。RT与LT分别为换流变压器的等效电阻与电感。
MMC的控制系统采用d-q解耦控制策略控制换流站功率或电压,其结构如图1(b)所示。MMC控制系统包括4个一阶惯性测量环节与4个PI控制器,其状态空间方程包括8个微分方程[8]。控制器的输出为经d-q变换后的三相基频参考电压Ucd和Ucq,同时作为MMC主回路的输入[13]。
对于交流系统,采用理想电源与电阻和电抗串联的戴维南等值电路建立交流系统模型[21],如图1(c)所示,则d-q坐标系下交流母线(point of common coupling,PCC)的电压可以表示为:
(2)
式中:Ued和Ueq是理想交流电压源的电压;Rac和Lac分别是交流系统的等效电阻和电抗。
MMC-MTDC的直流系统由直流传输线和换流站端部的平波电抗器组成[21]。将平波电抗器等效到线路串联电感中,采用电阻电感串联电路建立直流系统的等效模型为
(3)
式中:Udc1和Udc2为直流线两端的直流电压;Rd和Ld为等效电阻和电感。
1.2 MMC-MTDC系统小信号模型
联立MMC主回路、控制系统与交流系统的状态空间模型,可以得到单端MMC换流站的12阶状态空间模型为
(4)
式中x和u分别为系统的状态变量与输入变量。
将式(4)在某一稳定工作点附近线性化,则单端MMC换流站的小信号模型为
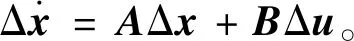
(5)
式中状态变量矩阵可以表示为
式中:isdm、isqm、usdm、usqm分别为Isd、Isq、Usd、Usq的测量值;x1、x2、x3、x4分别为4个PI控制器误差信号对时间的积分。
输入变量矩阵Δu可以表示为
式中Pref、Qref、Udcref分别为有功功率、无功功率和直流电压的参考值。
联立式(3)和式(5),得到由n个换流站组成的MMC-MTDC完整小信号模型为
(6)
式中:Asys为n端MMC-MTDC系统的状态空间矩阵,为12n-1阶方阵;Δxsys为系统的状态变量矩阵,为12n-1阶列向量。
为提高MMC-MTDC系统的稳定裕度,首先建立以特征根为目标函数的控制参数优化问题,并提出基于控制参数灵敏度的优化算法以协同优化多个控制参数。
根据式(6),一个n端柔性直流输电系统含有12n-1个特征值。分析这些特征值就能判断系统的小信号稳定性,当所有的特征值都在复平面的左半平面时,系统是稳定的。当系统运行在某个稳定的运行点时,特征值的大小取决于控制器参数。
在12n-1个特征值中,特征值的实部能够反映暂态过程衰减速度的快慢,且距离虚轴越远,其衰减速度越快,系统的稳定裕度越大,因此,距离虚轴最近的特征值可以反映所研究系统的稳定裕度。为提高系统的稳定裕度,应使距离虚轴最近的特征值尽量远离虚轴,则优化问题可以构造为:
(7)
i=1,2,…,n。
式中:λg为系统状态空间系数矩阵Asys的特征值;kLB、kUB分别为对应控制参数的下限与上限。
由于参数灵敏度能反映参数变化时特征值的变化方向和幅度[22],因此可以为控制参数的调整提供指导。所提出的控制参数优化算法的流程如图2所示。

图2 基于灵敏度的控制参数优化算法流程图Fig.2 Flowchart of the sensitivity analysis-based control parameter optimization algorithm
优化算法具体步骤如下:
第一步:初始化。通过小信号建模获得系统状态空间系数矩阵Asys。
第二步:特征值分析与优化问题的建立。通过式(6)计算Asys的特征值,选择距离虚轴最近的特征值λ1建立优化问题式(7)。
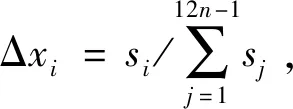
第四步:确定迭代步长。在确定优化方向后,需要决定优化步长。在优化过程中,若采用定步长优化,步长选择过大,可能会跳过最优点,引起震荡;步长选择过小,可能会导致收敛速度太慢。BLS是求解优化问题中调整搜索步长的有效方法,也是实际应用中的常用方法[23],其有效解决了优化过程中采取定步长的问题。回溯直线搜索的主要思想是首先给定初始步长,若初始步长不满足条件,则根据需要缩短步长,直到找到步长满足条件[24]。回溯直线搜索的具体过程如下:对于第三步中建立的控制参数调整梯度矩阵Δx,令初始步长t=1。若步长t不满足F(x+tΔx) 第五步:调整控制参数。根据灵敏度梯度矩阵,分配第四步中获得的迭代步长对控制参数进行调整,即Δli=tΔxi。若控制参数超过给定的下限或上限,则将其设置为相应的边界值。 第六步:终止条件。如果满足终止条件,终止迭代,输出优化后的控制参数。本算法的终止条件包括: 终止条件1:目标函数两次迭代结果的差值小于给定的收敛误差。 终止条件2:在距离虚轴次远的特征值与距离虚轴最近的特征值变化方向相反的情况下,距离虚轴次近的特征值与距离虚轴最近的特征值的差值小于给定的收敛误差。 选用一个三端MMC-MTDC系统测试所提出控制参数优化方法,其拓扑结构如图3所示。三端MMC-MTDC系统中,换流站1采用定直流电压,定无功功率控制方式,其无功功率设定值为0 MVar;换流站2采用定有功功率,定无功功率控制方式,其功率设定值为600 MW与0 MVar;换流站3采用定有功功率,定无功功率控制方式,其功率设定值为-200 MW与0 MVar。三端MMC-MTDC系统的参数如表1所示。 图3 三端MMC-MTDC系统结构图Fig.3 Structure diagram of a three-terminal MMC-HVDC transmission system 表1 三端MMC-MTDC仿真模型主要参数Table 1 Main parameters of the three-terminal MMC-MTDC simulation model 在PSCAD/EMTDC中建立如图3所示的三端MMC-MTDC系统。为验证小信号模型的有效性,换流站2的有功功率参考值在t=0.5 s时从600 MW阶跃变化至660 MW。图4为所建立的小信号模型与PSCAD仿真模型的动态响应结果。 图4 小信号动态模型与PSCAD中仿真模型的动态响应比较Fig.4 Dynamic response comparison between the proposed small-signal dynamic model and the nonlinear model in PSCAD 有功功率和直流电网电压的动态响应与仿真结果之间良好的一致性证明了所建立的小信号模型的有效性。暂态过程中存在微小差异的主要原因是在小信号建模过程中的线性化误差和建模过程中忽略MMC换流站内部动态谐波。 计算三端MMC-MTDC的所有特征值与控制系统状态变量相关比,分析特征值与控制系统的相关性,如图5所示。控制系统相关比的定义为 (8) 式中pki为状态变量xk对特征值λi的相关因子。 从图5可以看出,λ1与控制系统状态变量的相关比最大,对控制参数进行优化能够有效地改变λ1的分布,继而提升系统稳定裕度。 图5 三端MMC-MTDC特征值控制系统相关比Fig.5 Control system relative coefficients of the eigenvalues of three-terminal MMC-HVDC transmission system 在上述三端MMC-MTDC系统中应用所提出的控制参数优化方法提升系统稳定裕度。优化前后系统所有特征值均位于复平面的左半平面,系统是稳定的,且通过控制参数优化,系统距离虚轴最近的特征值由-3.891变为-5.093,远离虚轴,系统稳定裕度增大。图6为目标函数在优化过程中的变化情况,可以看出,在优化过程中,目标函数单调减小,没有出现震荡现象,每次迭代的结果均能单调地提高系统的稳定性裕度。 图6 目标函数轨迹Fig.6 Trajectories of the objective function 分别在PSCAD/EMTDC对三端MMC-MTDC施加不同的扰动,比较三端MMC-MTDC系统在原始参数与优化后参数情况下遭受扰动时的动态响应,以验证所提出的控制参数优化方法的有效性。 算例1:有功功率参考值变化。 换流站2的有功功率参考值在t=0.5 s时从600 MW阶跃变化至900 MW,参数优化前后3个换流站的有功功率响应与直流电网电压响应如图7所示。 从图7可以看出,控制参数优化后,换流器有功功率和直流电网电压的波动明显变小,其中换流站1的有功功率超调量由优化前的57.01 MW下降至优化后的30.32 MW;换流站3的有功功率波动由优化前的0.870 3 MW下降至优化后的0.266 5 MW;直流系统过电压由27.71 kV下降到17.96 kV。由此可见,三端MMC-MTDC输电系统控制参数优化后系统的稳定性增强。 图7 换流站2有功功率参考值变化时,优化前后有功功率和直流电网电压的动态响应比较Fig.7 Dynamic response of active power and DC voltage before and after optimization when active power reference changes 算例2:直流电压参考值变化。 换流站1的直流电压参考值在t=0.5 s从±320 kV阶跃下降至±300 kV,3个换流站有功功率和直流电网电压的动态响应如图8所示。 图8表明三端MMC-MTDC系统在采用优化后的控制参数时,有功功率和直流电网电压的波动得到了有效地抑制,其中,换流站1的有功功率波动最大幅度从184.95 MW减小到166.18 MW,换流站2的有功功率波动最大幅度从1.25 MW减小到0.69 MW,换流站3的有功功率波动最大幅值从1.235 MW减小到0.35 MW,直流系统电压超调量从15.39 kV减小到10.17 kV,表明控制参数优化后系统的稳定性增强。 图8 直流电压参考值变化时,优化前后有功功率和直流电网电压的动态响应比较Fig.8 Dynamic response of active power and DC voltage before and after optimization when DC voltage reference change 算例3:直流电网短路故障。 在t=0.5 s时,在换流站1和换流站2之间的直流线路中点发生故障电阻为10 Ω的极间短路故障,0.05 s后故障清除。图9比较了在故障期间,控制参数优化前后换流站有功功率和直流电网电压的动态响应。 图9 直流侧发生两极间短路时,优化前后有功功率和直流电网电压的动态响应比较Fig.9 Dynamic response of active power and DC voltage under a pole-to pole short circuit fault before and after optimization 图9的结果表明,当控制器采用优化后的控制参数时,故障清除后直流电网电压波动显著减小,恢复时间明显缩短,换流站有功功率的振荡幅度显著减小。因此,采用优化后的控制参数显著提升了三端MMC-MTDC系统的稳定裕度。 为验证所提出方法的有效性,采用粒子群算法[25]对上述三端MMC-MTDC系统的控制参数进行优化。所提出的优化方法与粒子群算法的目标函数轨迹如图10所示。多次运行粒子群算法,其平均收敛迭代次数为58次。 图10 目标函数轨迹比较Fig.10 Comparison of the trajectories of the objective functions 对比2种方法的优化结果与优化效率,可以发现: 1)基于参数灵敏度的优化算法迭代次数较少,收敛速度较快;粒子群算法搜索初期收敛速度快,但搜索后期收敛速度变慢,且迭代次数较多。 2)基于参数灵敏度的优化算法通过参数灵敏度确定优化方向,使每一次迭代结果都能单调地向最优解靠近;粒子群算法的惯性权重系数、学习因子等参数的选择具有随机性,优化效果依赖于这些参数,且每次优化的结果可能不同。 3)基于参数灵敏度的优化算法可以采用已有的控制参数作为初值,能够充分利用控制器的先验知识;粒子群算法随机产生控制参数的初值,抛弃已有控制器的先验知识是一种浪费。 综上所述,所提出的基于参数灵敏度的优化方法从优化结果与优化效率上均优于粒子群算法。 针对MMC-MTDC系统提出了一种基于参数灵敏度的控制参数优化方法。建立了包括MMC主回路、控制系统、交流系统和直流系统的MMC-MTDC小信号模型,为控制系统参数优化奠定基础。建立了以特征值为优化目标的控制参数优化问题,并提出了一种基于参数灵敏度的控制参数优化算法以提升MMC-MTDC系统的稳定裕度。在三端MMC-MTDC系统中应用所提出的控制参数优化方法进行稳定性分析和时域仿真,结果表明采用所提出的方法优化控制参数后,系统的稳定性显著提升。最后比较了所提出的控制参数优化算法与粒子群算法的优化结果与优化效率,验证了本方法的优越性。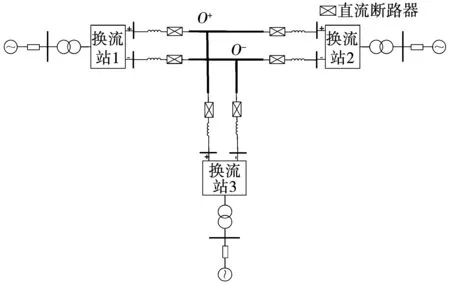
3.1 小信号模型验证

3.2 三端MMC-MTDC的控制系统相关比分析
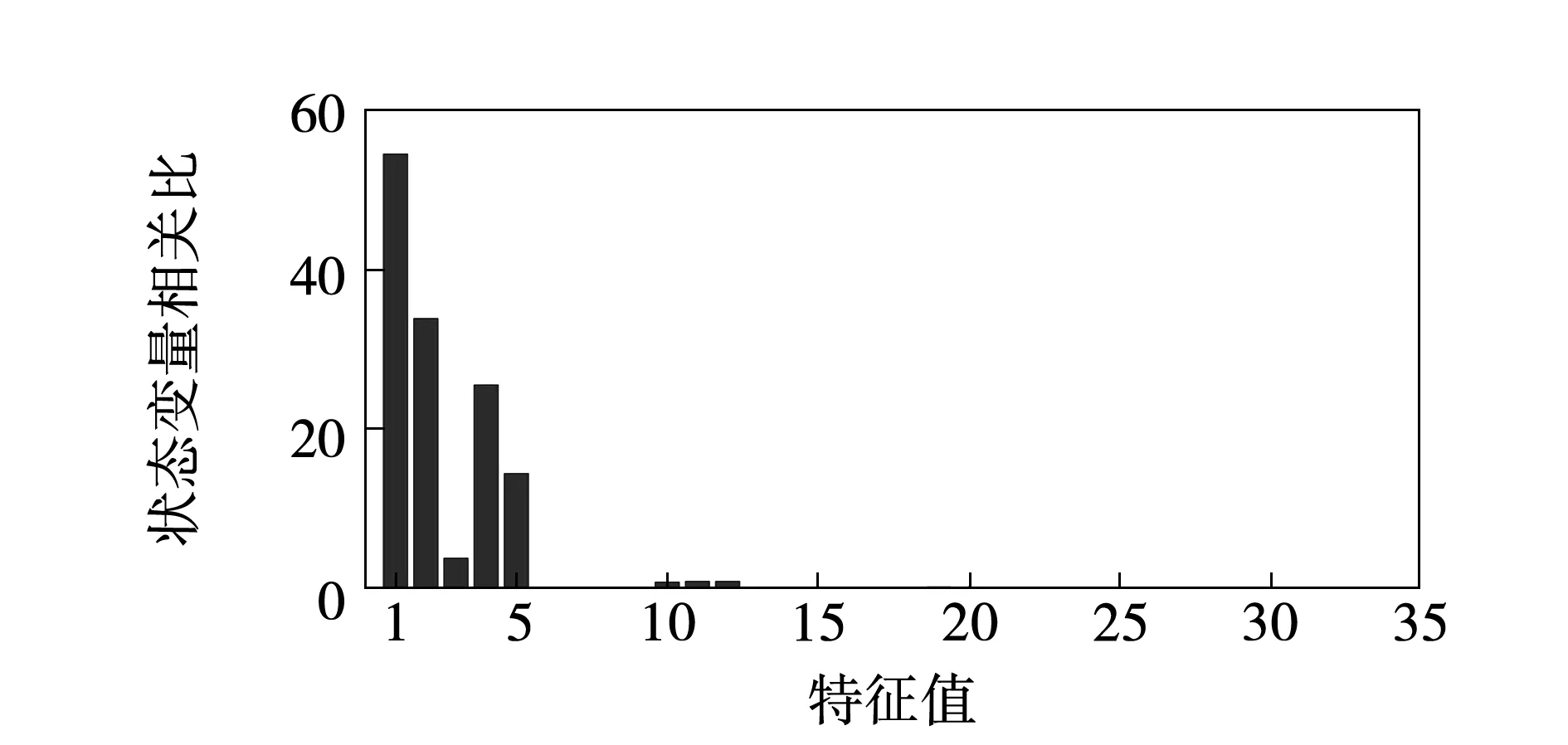
3.3 稳定性分析

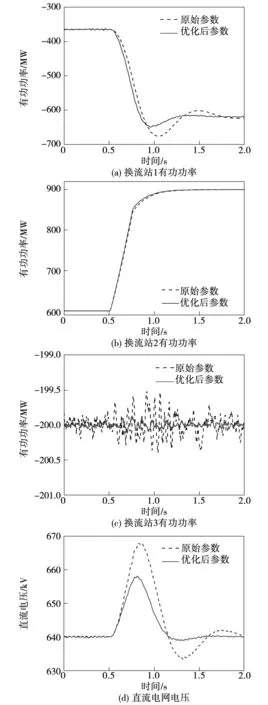
3.4 仿真验证


3.5 优化算法性能讨论

