永磁同步电机模糊自适应变开关次数权重系数模型预测转矩控制

李耀华，秦辉，苏锦仕，秦玉贵，赵承辉，周逸凡

(长安大学 汽车学院，西安 710064)

0 引 言

模型预测转矩控制(model predictive torque control,MPTC)基于电机系统预测模型，遍历计算施加不同电压矢量后下一时刻电机磁链和转矩值，并由此得到不同的成本函数值，从备选电压矢量集合中选择令成本函数最小的电压矢量作为最优电压矢量，近年来成为了永磁同步电机(permanent magnet synchronous motor,PMSM)控制领域研究的热点[1-6]。

不同于矢量控制与直接转矩控制，模型预测控制采用成本函数来评价施加电压矢量对系统的作用效果。成本函数作为模型预测转矩控制选择电压矢量的唯一标准，对系统的性能起着重要的作用。成本函数具有较大的柔性，可将不同性质的控制目标或控制变量统一在一个成本函数中，兼顾多个控制目的，实现系统的综合性能优化。这也是模型预测转矩控制的优势之一。

减小开关频率对减小开关损耗、提高电机控制系统效率有着重要的意义。但传统模型预测转矩控制成本函数一般仅将转矩与磁链作为控制目标，并未考虑减小开关次数，使得逆变器开关频率较高，增加了系统损耗[7-8]。文献[9]从备选电压矢量出发，根据当前逆变器开关状态，以降低开关次数为原则来确定下一控制周期的可选电压矢量集合。该方法不仅降低逆变器的开关频率，也有利于减少模型预测控制算法的计算量，但是该方法无法对开关次数和控制性能的重要性进行调节，没有利用成本函数的灵活性。为了兼顾控制性能与系统开关次数，实现多目标优化，文献[10-11]将开关次数控制引入至成本函数，但并未给出开关次数权重系数的具体确定方法。文献[12]将降低开关频率也设定为控制目标之一，并采用搜索法设计权重系数，但其设计的权重系数为固定值。当系统状态变化时，固定的权重系数不能保证控制目标的重要性随系统状态变化而实时调节。为了适应多变的系统状态，文献[13-14]以优化系统对转矩与磁链的控制效果，选择磁链误差和转矩误差作为模糊控制器的输入、输出可调的转矩权重系数与磁链权重系数。文献[15]基于模型预测电流控制，以转速偏差及转速变化率为模糊控制的输入，分别输出d-q 轴电流控制的权重系数和开关次数的权重系数。文献[16]将转矩、转矩误差及磁链误差作为模糊控制的输入，也采用模糊控制动态调节权重系数。

本文基于定子磁链坐标系的表面式永磁同步电机模型预测转矩控制系统，将减小开关次数作为成本函数控制目标之一，采用搜索法确定了开关次数权重系数。提出自适应变权重系数控制策略，确定了稳态开关次数权重系数。仿真结果表明：自适应变权重系数可在对平均开关频率减小效果相当条件下，减小磁链和转矩脉动。模型预测转矩系统的不同控制目标重要性应随着系统状态动态变化。因此，表征控制目标相对重要性的权重系数也应是动态变化的。本文进一步提出模糊自适应变权重系数控制策略，采用模糊控制动态输出稳态开关次数权重系数。仿真结果表明：模糊自适应变权重系数根据电机实时运行状态动态由模糊控制器输出稳态开关次数权重系数，从而进一步降低逆变器平均开关频率、电机转矩与磁链脉动。

基于定子磁链坐标系，表面式永磁同步电机(surface permanent magnet synchronous motor,SPMSM)定子磁链幅值和转矩的预测模型[17-20]分别为：

(1)

(2)

式中：ψs(k)、Te(k)和δ(k)分别是k时刻的定子磁链幅值、转矩和转矩角；Vs(k)和α为施加电压矢量的幅值及电压矢量与定子磁链的夹角；p为电机极对数；ψf为转子磁链；Ld为d轴电感；Δt为系统采样周期。

模型预测转矩控制备选电压矢量采用逆变器产生的全部7个基本电压矢量，表达式为

Vs∈{V0,V1,V2,V3,V4,V5,V6}。

(3)

式中：Vs为施加电压矢量；V0～V6为逆变器产生的7个基本电压矢量。零电压矢量可由两个开关状态(111或000)生成，具体选择以开关次数最小为原则[21]。

传统模型预测转矩控制成本函数如下式所示，其仅考虑磁链和转矩控制，未考虑减小开关次数。

(4)

表面式永磁同步电机模型预测转矩控制系统如图1所示。

图1 表面式永磁同步电机模型预测转矩控制系统Fig.1 MPTC system of SPMSM

传统模型预测控制中逆变器开关频率较高，为减少逆变器的能量损耗与发热，本文将降低平均开关频率作为附加控制目标包含进成本函数优化过程中。考虑到逆变器平均开关频率的计算周期与电机磁链和转矩计算周期不匹配，本文取逆变器在每个控制周期中的开关次数作为控制变量，消除了三者计算周期不匹配的矛盾。考虑降低逆变器开关频率的模型预测转矩控制成本函数表达式为

λswnsw。

(5)

式中：λsw为降低开关频率项的权重系数；nsw为所选电压矢量引起的开关次数。

权重系数体现了控制目标在成本函数中的重要程度，其大小将直接影响到系统性能。所以正确设计权重系数对电机系统性能优化至关重要。本文以0为初始值，逐步增大权重系数，根据不同权重下磁链、转矩及平均开关频率的变化，选择最优权重系数[8]。

在MATLAB/Simulink环境中建立了表面式永磁同步电机模型预测转矩控制仿真模型。仿真模型的采样周期为5×10-5s；逆变器直流母线电压为312 V。仿真用表面式永磁同步电机参数如表1所示。

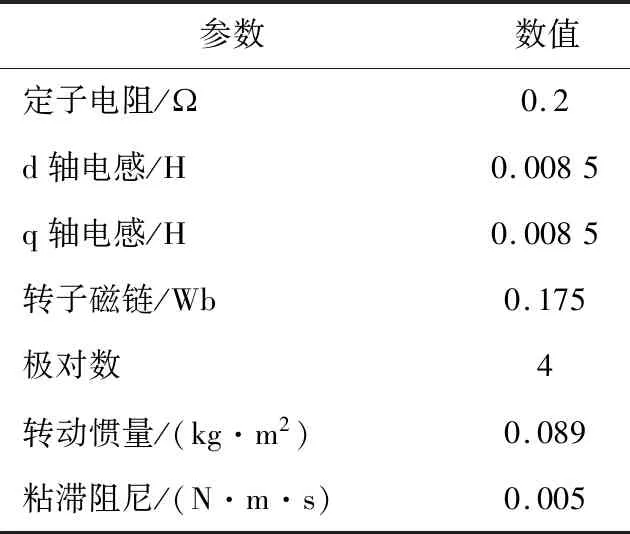
表1 仿真用表面式永磁同步电机参数Table 1 Parameters of SPMSM for simulation

定义稳态(0.5～2 s)转矩脉动均方根误差(root mean squared error,RMSE)、稳态磁链脉动RMSE、平均开关频率和评价函数平均值分别为

(6)

(7)

(8)

(9)

式中：n为采样点总个数；Nswitching为逆变器开关总次数；t为采样总时长。

开关次数权重系数需通过反复试验来获得：给定电机参考转速为30 r/min，负载转矩为20 N·m，定子磁链采用恒幅值控制，仿真时长为2 s。令开关次数权重系数初始值为0，以合适的步长(本文取0.001)逐步增大权重系数。采用不同权重系数λsw进行循环仿真试验，系统控制性能由以上定义的评价指标来量化，结果如表2和图2～图5所示。

表2 不同λsw下电机系统性能Table 2 Performance of motor system under different λsw

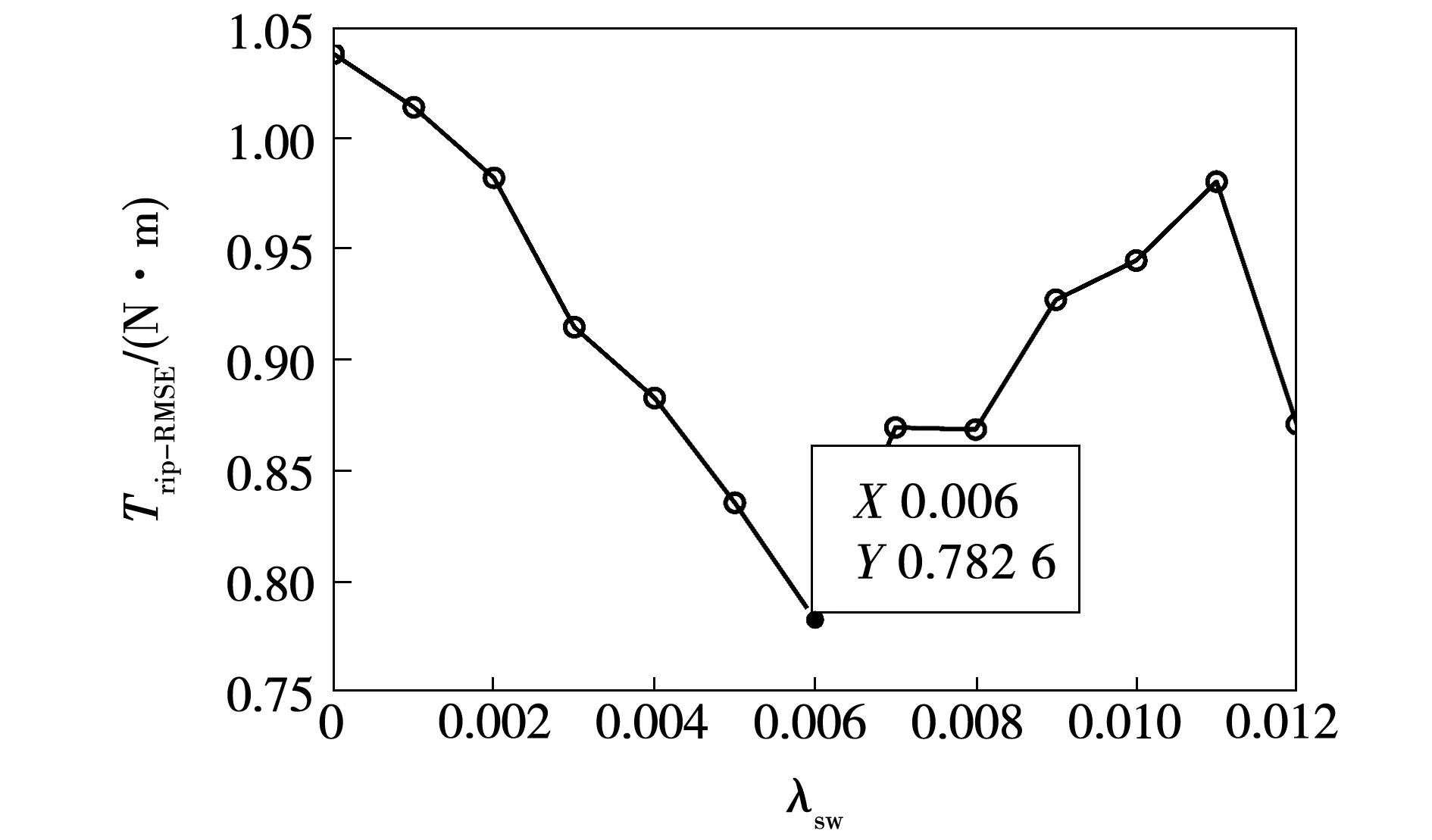
图2 不同λsw下转矩脉动均方根误差Fig.2 RMSE of torque ripple under different λsw

图3 不同λsw下磁链脉动均方根误差Fig.3 RMSE of stator flux ripple under different λsw

图4 不同λsw下平均开关频率Fig.4 Average switching frequency under different λsw

图5 不同λsw下评价函数平均值Fig.5 Average value of evaluation function under different λsw

仿真结果表明，随着开关次数权重系数的递增，逆变器的平均开关频率明显下降，但电机的磁链脉动与转矩脉动也有所增加。同时仿真试验表明：当权重系数大于0.013，模型预测控制系统过多偏重减小开关次数，此时选择电压矢量不能满足磁链和转矩控制要求，转矩与磁链脉动过大，导致电机转速不能正常跟踪参考转速，系统无法对电机有效控制，出现失控。因此，考虑到电机转矩和磁链的控制性能，采用固定权重系数的成本函数应避免选取过大的开关次数权重系数。这使该控制策略降低开关频率的能力受到了限制。兼顾电机的综合性能，本文选择权重系数λsw为0.006。

上文所提的权重系数固定的成本函数当开关次数权重系数较大时，系统减弱对磁链和转矩的控制，导致系统失控。当系统处于动态时，由于没有调节磁链和转矩控制的重要程度，也会导致系统失控。因此，采用固定的权重系数对系统性能提升有限，无法满足电机系统控制目标重要性动态变化的实际要求。因此，需要根据系统状态动态调整权重系数。本文提出一种变权重系数的成本函数，根据磁链与转矩控制效果实时调节开关次数的权重系数。当磁链或转矩脉动过大时(磁链脉动大于0.02 Wb或转矩脉动大于1 N·m)，系统处于动态，令开关次数权重系数为0，此时模型预测转矩控制仅考虑控制磁链和转矩，迅速减小磁链脉动或转矩脉动，防止系统失控。否则，系统处于稳态，此时选用较大的权重系数以减小开关次数，降低逆变器开关频率。

基于自适应变权重系数成本函数的模型预测转矩控制流程如图6所示。

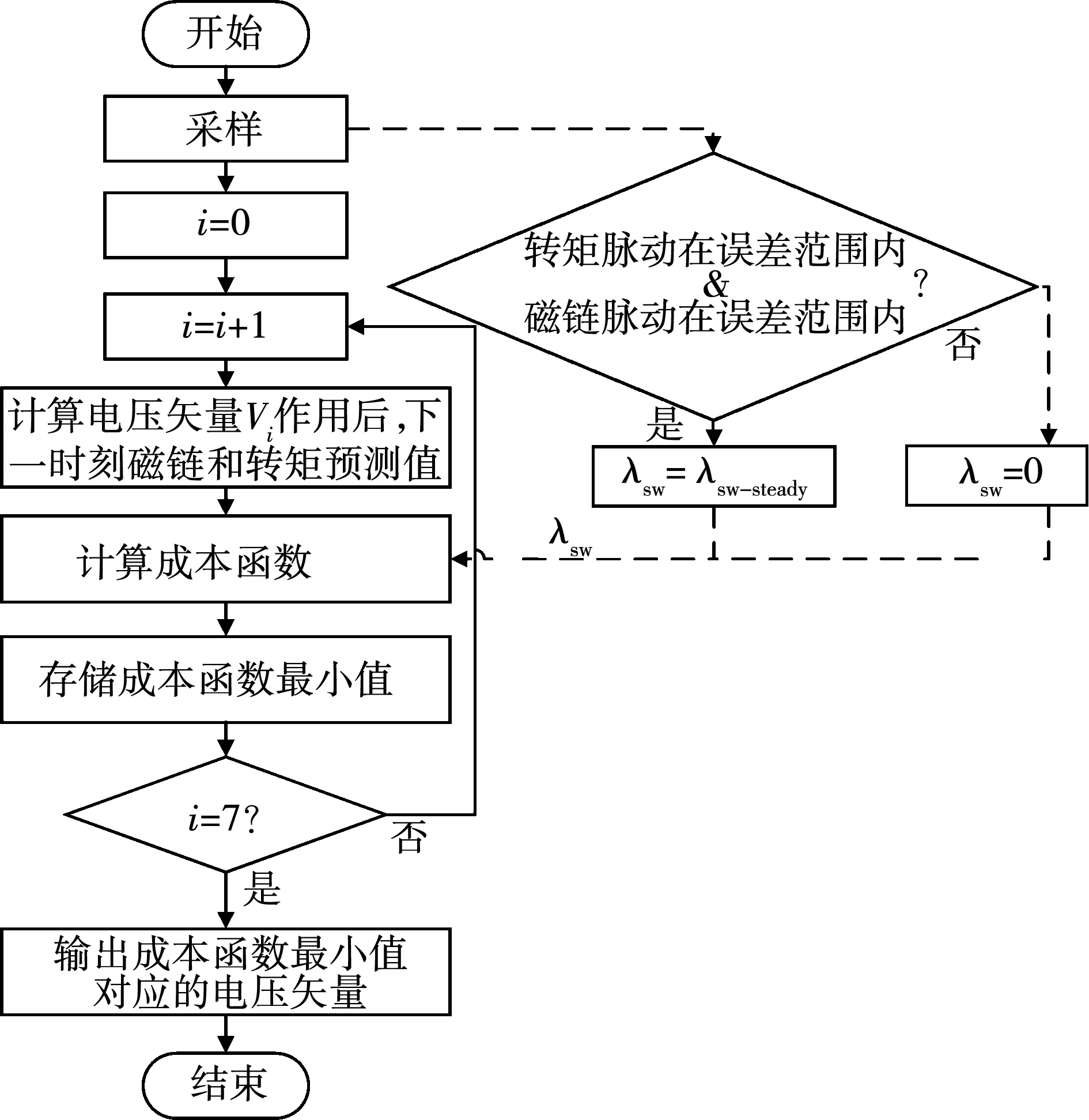
图6 基于自适应变权重系数的模型预测转矩控制流程Fig.6 Flow chart of the MPTC using adaptive dynamic weight coefficient

依然采用搜索法确定系统处于稳态时的开关次数权重系数λsw-steady，令其初始值为0，并逐步增大。在不同λsw-steady下，转矩脉动RMSE、定子磁链脉动RMSE、逆变器平均开关频率、评价函数平均值及系统稳态时间占比如表3和图7～图10所示。

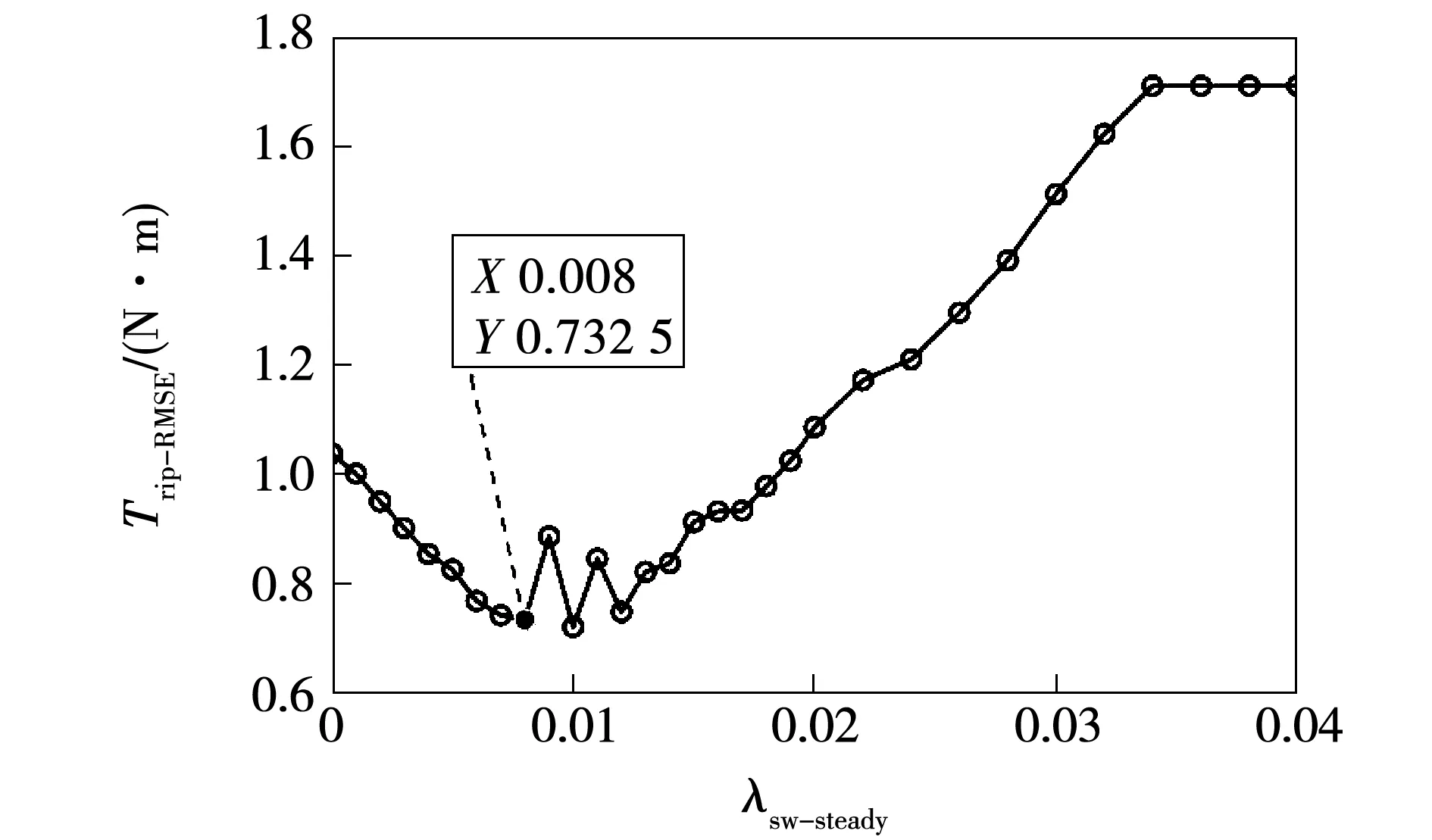
图7 不同λsw-steady下转矩脉动均方根误差Fig.7 RMSE of torque ripple under different λsw-steady

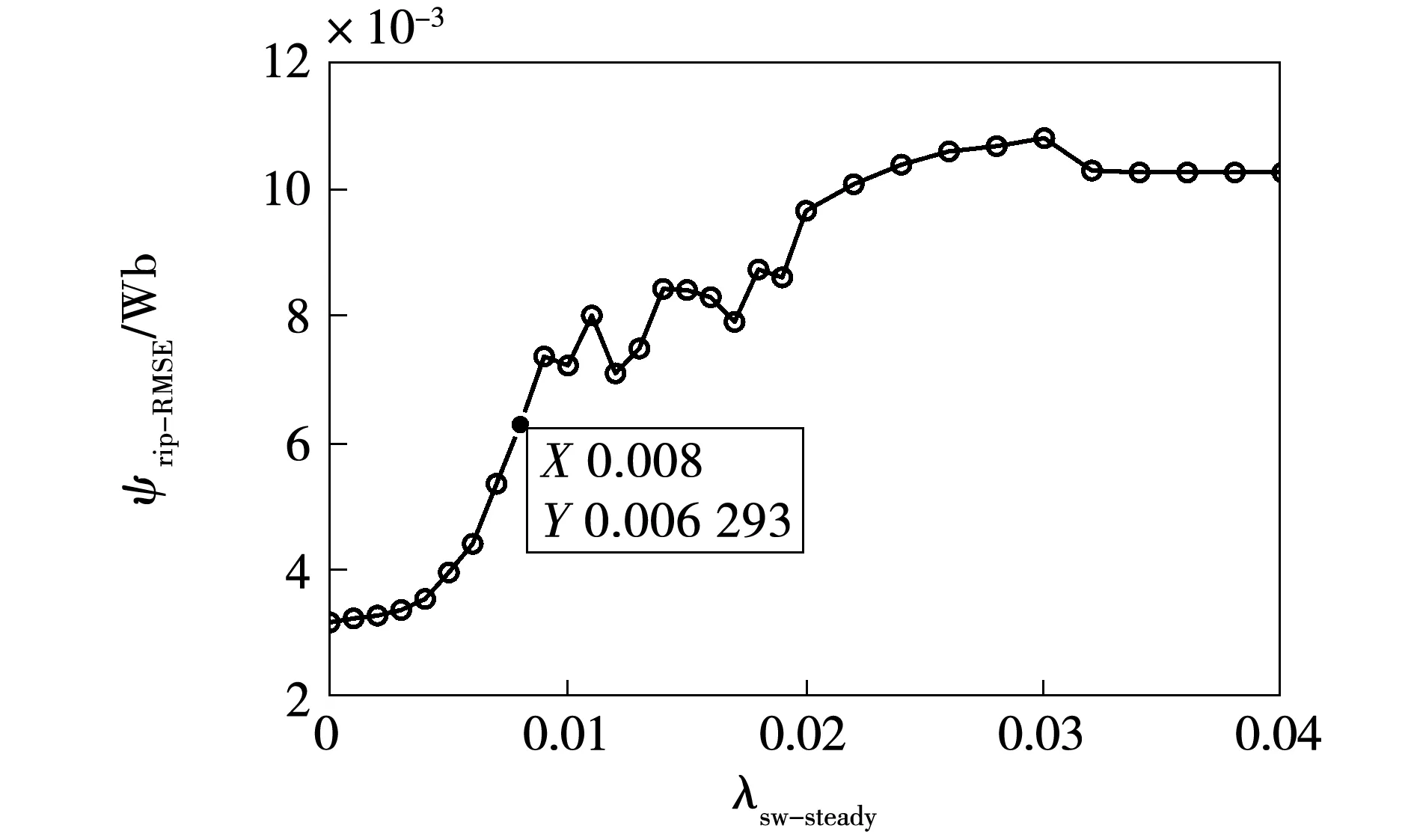
图8 不同λsw-steady下磁链脉动均方根误差Fig.8 RMSE of stator flux ripple under different λsw-steady

图9 不同λsw-steady下平均开关频率Fig.9 Average switching frequency under different λsw-steady

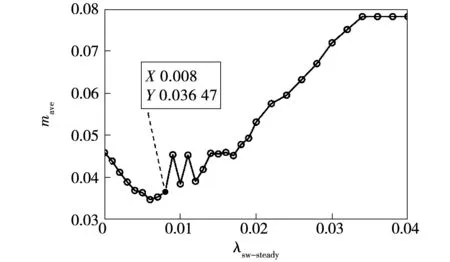
图10 不同λsw-steady下评价函数平均值Fig.10 Average value of evaluation function under different λsw-steady

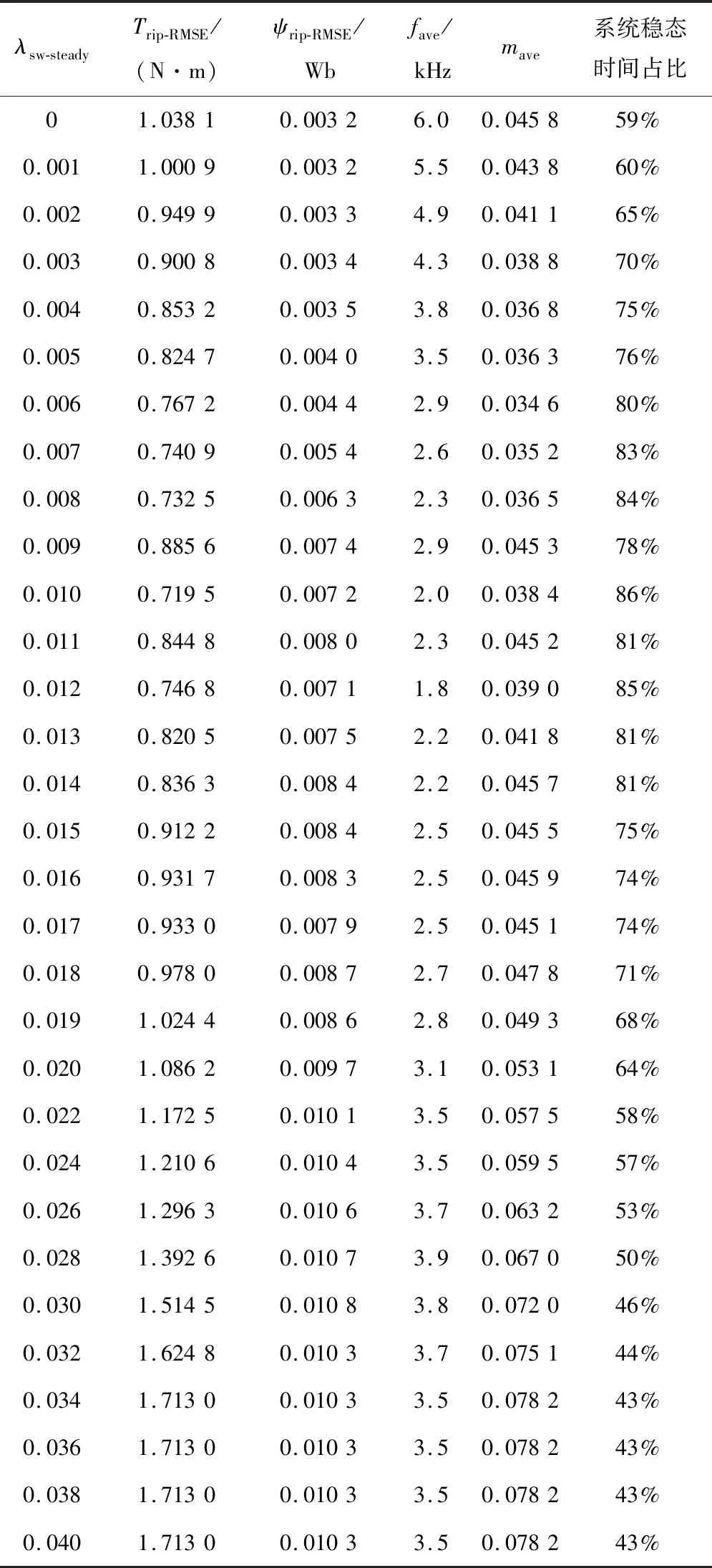
表3 不同λsw-steady下电机系统性能Table 3 Performance of motor system under differentλsw-steady

仿真结果表明，随着λsw-steady的递增，平均开关频率降低，且转矩和磁链脉动始终在可控范围内。但当λsw-steady大于0.012之后，平均开关频率反而开始增大。当λsw-steady大于0.034之后，平均开关频率、磁链和转矩脉动均保持稳定。这是因为随着稳态权重系数的增大，系统逐步减弱对磁链和转矩的控制，使得转矩和磁链脉动增大，系统稳态时间占比减小，从而减小了稳态下使用权重系数来降低开关次数的时间，使得电机的转矩与定子磁链脉动增加，系统平均开关频率增大，并最终达到平衡。兼顾电机的综合性能，本文选择λsw-steady为0.008。

上文采用了统一的试验条件，以便正确设计权重系数λsw-steady。而电机实际运行工况是复杂多变的，单一的权重系数难以与多变的运行工况匹配。因此，λsw-steady的设计应考虑电机当前的运行工况，在线调整来实现最优控制。

给定电机参考转速为30 r/min，负载转矩Tm分别取10、20、30 N·m，令稳态权重系数λsw-steady初始值为0，以给定步长(取0.001)逐步增大λsw-steady。随着开关次数权重系数的递增，逆变器平均开关频率以及评价函数平均值如图11～图13所示。

图11 开关次数权重系数对电机性能的影响(Tm=10 N·m)Fig.11 Influence of λsw-steady on motor performance(Tm=10 N·m)

由图11～图13可得：当电机负载转矩分别为10、20、30 N·m时，合适的λsw-steady取值区间分别为[0.010,0.014]、[0.006,0.010]和[0.003,0.006]。由此可得，合适的λsw-steady的取值在一定程度上受到电机转矩的影响，随着电机转矩的增大，λsw-steady的取值应有所降低。

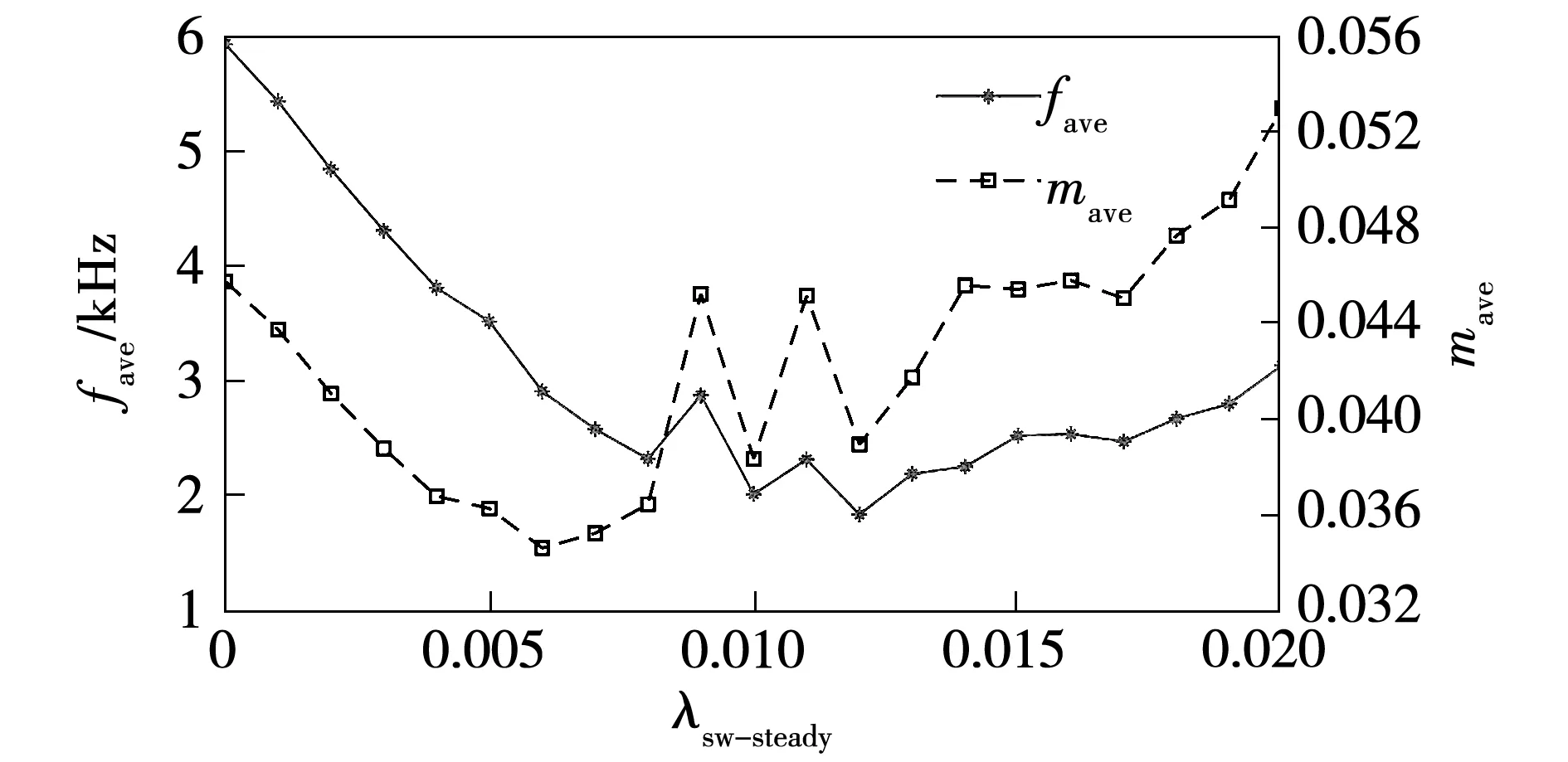
图12 开关次数权重系数对电机性能的影响(Tm=20 N·m)Fig.12 Influence of λsw-steady on motor performance(Tm=20 N·m)

图13 开关次数权重系数对电机性能的影响(Tm=30 N·m)Fig.13 Influence of λsw-steady on motor performance(Tm=30 N·m)

由上文可知，电机转矩对λsw-steady的选取存在一定的影响。同时考虑到电机在动态响应时，成本函数应更多地关注对转矩与磁链的控制，开关次数权重系数应降低，以保证系统具有良好的动态性能。因此，本文引入模糊算法，采用模糊控制动态输出合适的λsw-steady。模糊控制器的输入变量取电机转矩绝对值|Te|与转速误差Δn，输出则为稳态时开关次数权重系数λsw-steady。模糊变权重系数控制的开关次数权重系数确定流程如图14所示。

图14 模糊变权重系数控制的开关次数权重系数确定流程Fig.14 Process of determining λsw of adaptive dynamic weight coefficient using fuzzy control

电机转矩绝对值|Te|论域为[0 N·m,35 N·m]，分为5个模糊子集，记为{T1,T2,T3,T4,T5}，隶属度函数如图15所示。

图15 电机转矩绝对值隶属度函数Fig.15 Membership function of |Te|

转速误差Δn论域为[-5 r/min,5 r/min]，分为3个模糊子集，记为{N,Z,P}，隶属度函数如图16所示。

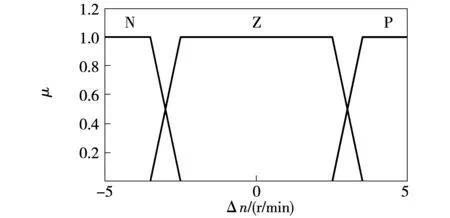
图16 转速误差隶属度函数Fig.16 Membership function of Δn

稳态权重系数λsw-steady论域为[0,0.017]，分为5个模糊子集，记为{λ1,λ2,λ3,λ4,λ5}，隶属度函数如图17所示。

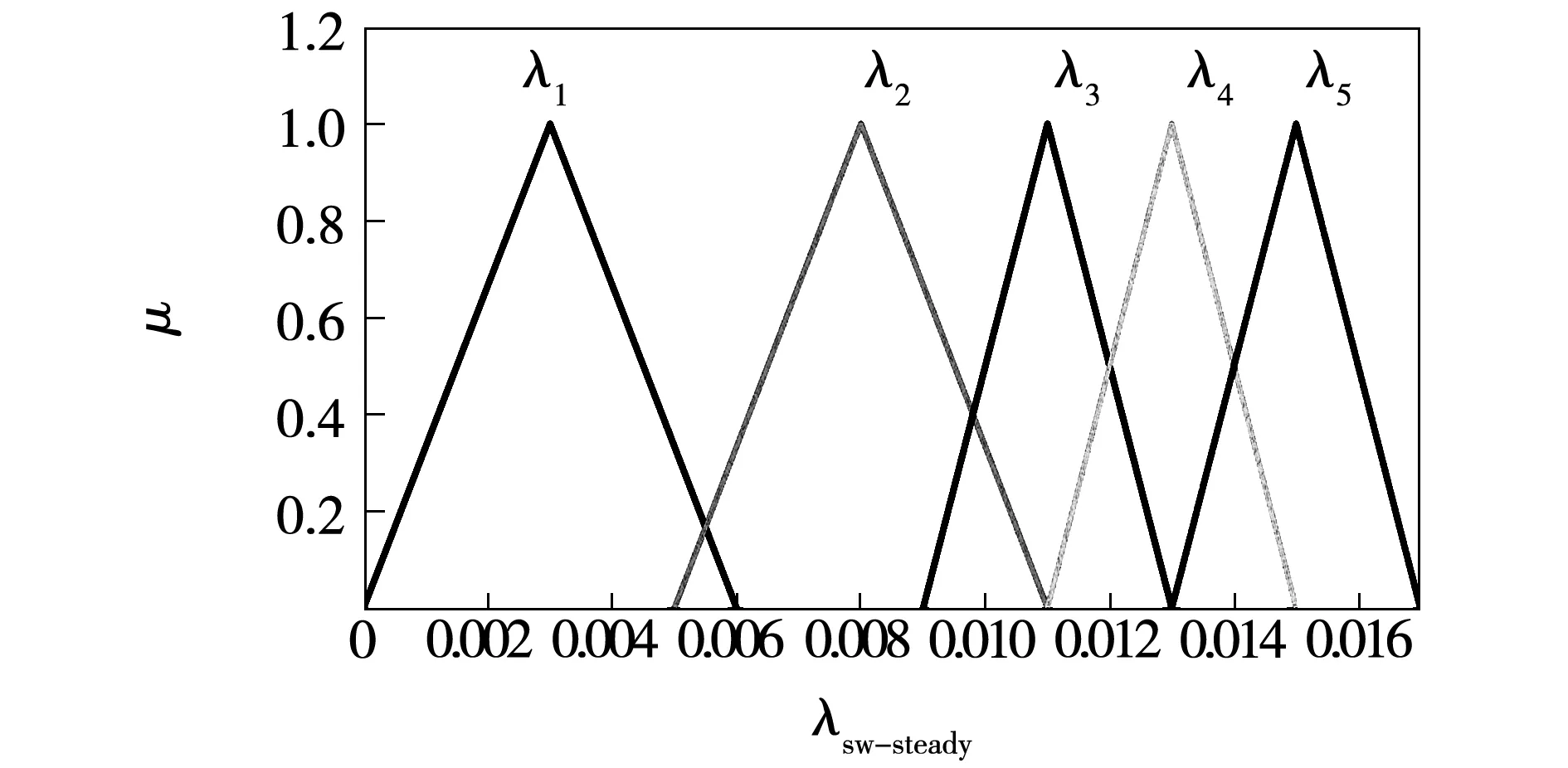
图17 稳态权重系数λsw-steady隶属度函数Fig.17 Membership function of λsw-steady

由上文可得：随着电机转矩的增大，λsw-steady的取值应有所降低。当电机转速误差Δn过小或过大时，表明电机当前转速偏离参考转速，处于动态响应过程，成本函数中的稳态权重系数λsw-steady也应减小，由此可得模糊控制规则表，如表4所示。模糊控制器采用经典的Mamdani模型，并以面积重心法反模糊化并输出。模糊推理输入-输出曲面如图18所示。

表4 模糊控制规则表Table 4 Fuzzy control rules

图18 模糊推理输入-输出曲面Fig.18 Input-output surface of fuzzy reasoning

仿真所用永磁同步电机模型预测转矩控制系统与上文保持一致。仿真条件的设定如下：总时长为10 s，电机由静止启动，参考转速初始为40 r/min，2 s时阶跃至80 r/min，6 s时阶跃至60 r/min。负载转矩初始值为15 N·m，4 s时阶跃至25 N·m，8 s时阶跃至10 N·m。分别采用传统模型预测转矩控制、固定权重系数(λsw=0.006)、自适应变权重系数(λsw-steady=0.008)及模糊自适应变权重系数控制四种控制方案进行对比验证，电机的转矩、磁链幅值以及开关次数权重系数分别如图19～图28所示。

图19 传统模型预测转矩控制下转矩Fig.19 Torque under the conventional MPTC

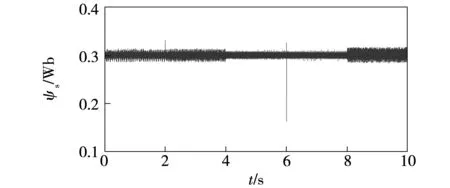
图20 传统模型预测转矩控制下定子磁链幅值Fig.20 Amplitude of stator flux under the conventional MPTC

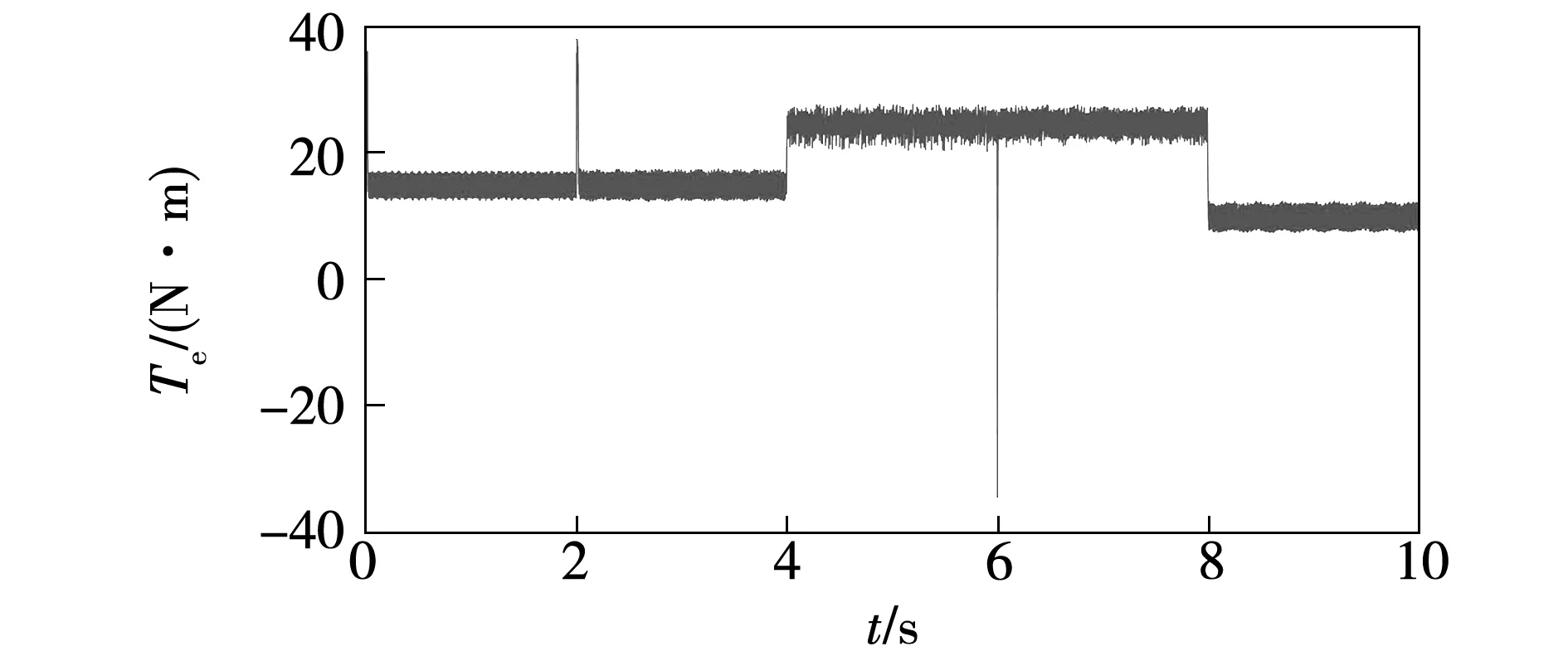
图21 固定权重系数控制下转矩Fig.21 Torque under the control of cost function with constant weight coefficient

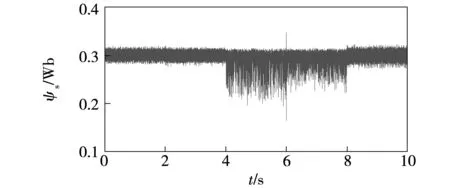
图22 固定权重系数控制下定子磁链幅值Fig.22 Amplitude of stator flux under the control of cost function with constant weight coefficient

图23 自适应变权重系数控制下转矩Fig.23 Torque under the control of cost function with adaptive dynamic weight coefficient

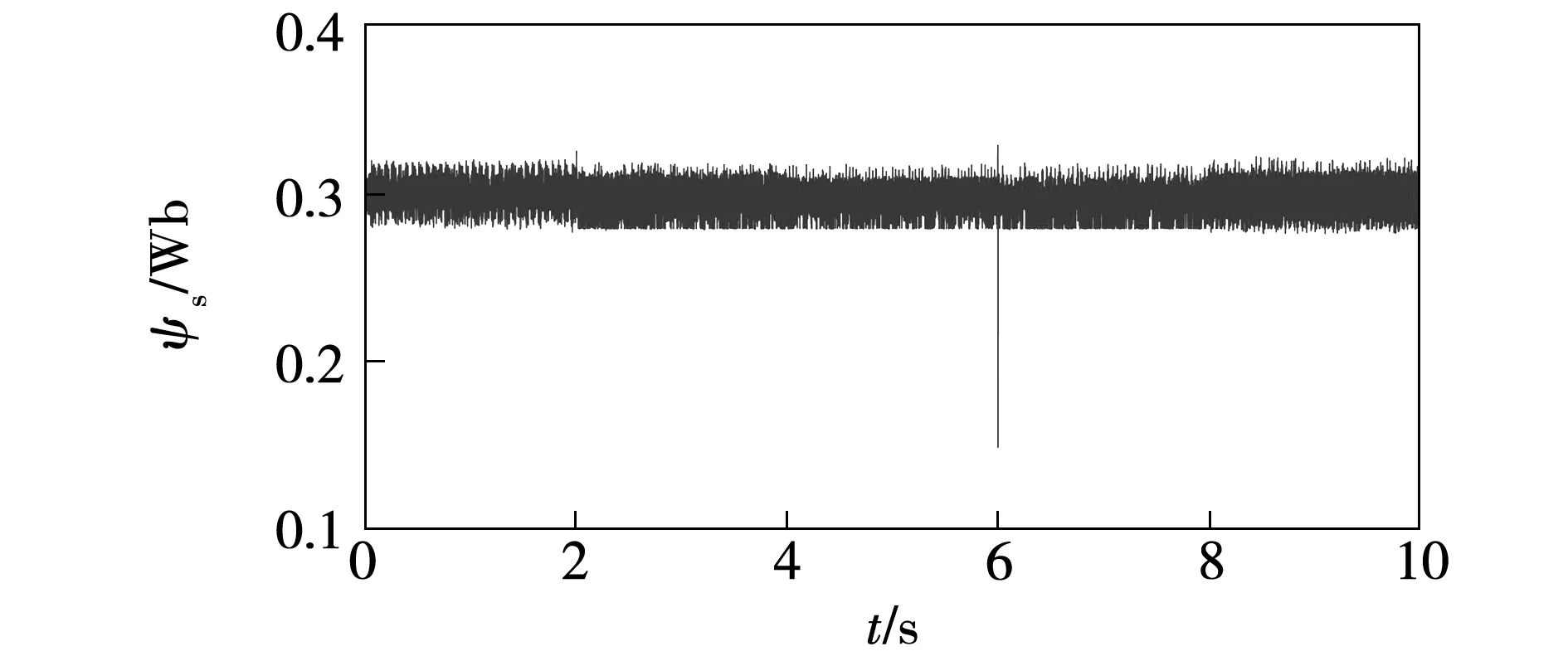
图24 自适应变权重系数控制下定子磁链幅值Fig.24 Amplitude of stator flux under the control of cost function with adaptive dynamic weight coefficient

图25 自适应变权重系数控制下开关次数权重系数Fig.25 λsw under the control of cost function with adaptive dynamic weight coefficient

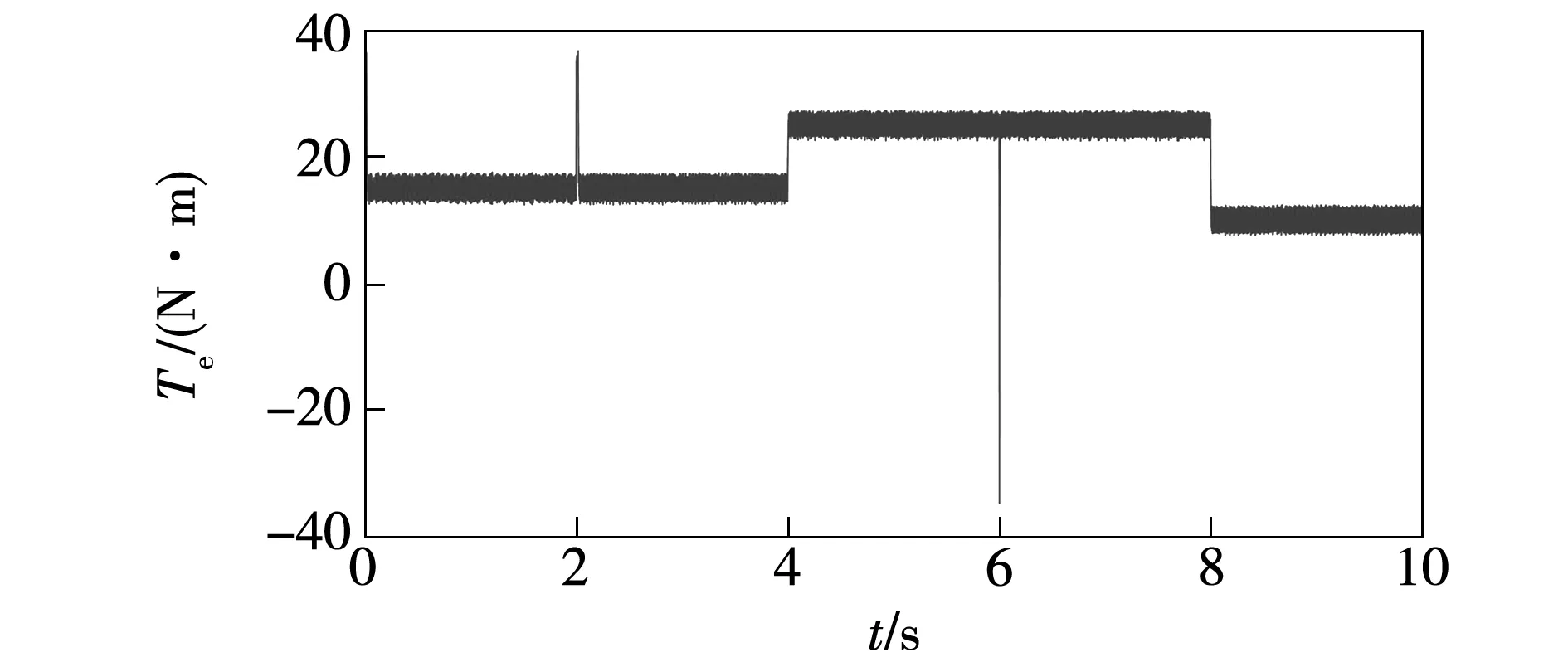
图26 模糊自适应变权重系数控制下转矩Fig.26 Torque under the control of cost function with adaptive dynamic weight coefficient using fuzzy control

图27 模糊自适应变权重系数控制下定子磁链幅值Fig.27 Amplitude of stator flux under the control of cost function with adaptive dynamic weight coefficient using fuzzy control

图28 模糊自适应变权重系数控制下开关次数权重系数Fig.28 λsw under the control of cost function with adaptive dynamic weight coefficient using fuzzy control

表5和表6分别给出了采用4种控制方案，电机性能指标和逆变器开关切换次数情况。

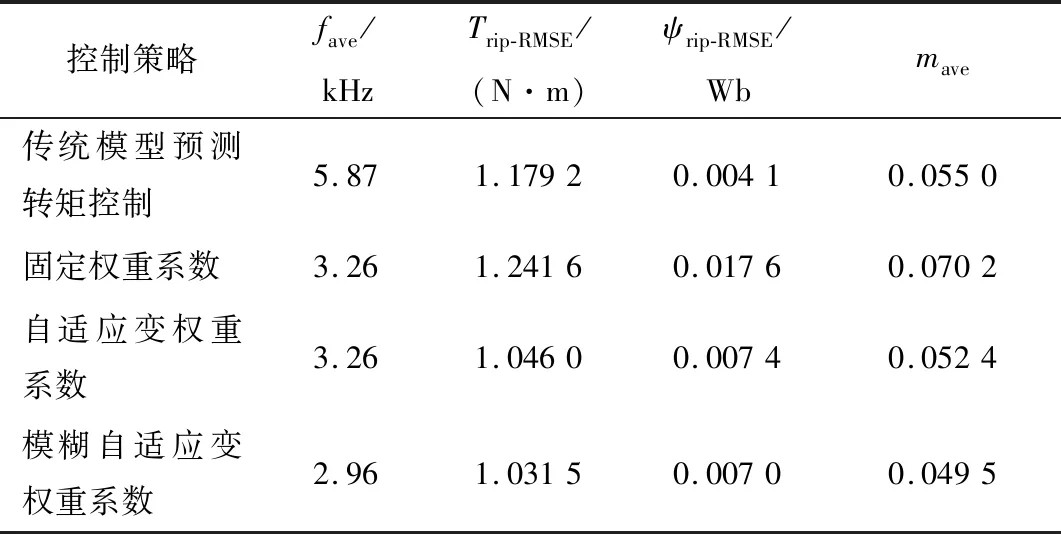
表5 不同控制策略下电机系统性能Table 5 Performance of motor system under different control strategies

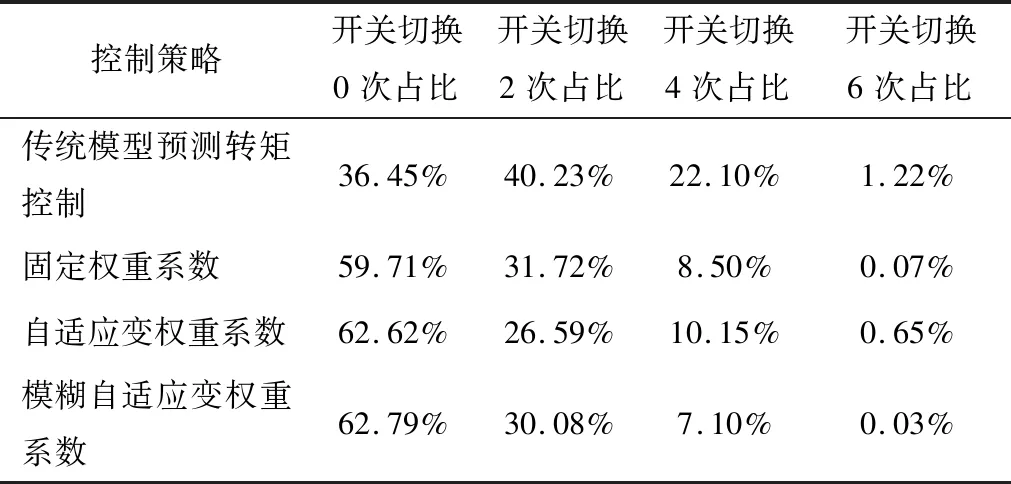
表6 不同控制策略下开关切换次数Table 6 Switching times under different control strategies

本文建立了表面式永磁同步电机模型预测转矩控制系统，并将降低平均开关频率作为附加控制目标包含进成本函数优化过程中，采用搜索法设计了开关次数权重系数，并进一步提出采用模糊算法动态输出稳态开关次数权重系数的模糊自适应变权重系数控制策略，结论如下：

1)成本函数易于包含所需的控制目标，将逆变器开关次数作为控制变量添加到成本函数中，在优化过程中，控制算法倾向于选择将会引起开关切换次数较小的电压矢量，因此可显著减小逆变器的平均开关频率。

2)自适应变权重系数可根据系统状态动态调整开关次数权重系数。系统动态时，令权重系数为0，保证系统稳定运行；系统稳态时，输出合适的稳态权重系数，以减小开关次数。基于搜索法确定的开关次数权重系数，固定权重系数和自适应变权重系数的成本函数对平均开关频率减小效果相当，自适应变权重系数可进一步减小磁链和转矩脉动。

3)固定权重系数的成本函数和自适应变权重系数的成本函数没有或部分考虑系统运行过程中控制目标重要性是动态变化的。模糊自适应变权重系数可根据电机运行状态，由模糊控制器输出稳态开关次数权重系数，可进一步降低逆变器平均开关频率，同时有效抑制了电机转矩脉动与磁链脉动。