考虑技术进步的DEA方法研究

王江泉,张 俊,赵 鑫

(1.福建师范大学 经济学院,福建 福州 350117;2.福建工程学院a.生态环境与城市建设学院,b.互联网经贸学院,福建 福州 350000)

一、引言

数据包络分析方法(DEA)是根据多项投入指标和多项产出指标,利用线性规划方法对同类对象进行相对有效性评价的一种非参数统计方法。该方法自美国著名学者Charnes等提出以来,广泛应用于各行各业[1]。它具有不用设定指标权重、不必统一量纲等优势,其基本模型是具有规模报酬不变(CRS)特征的CCR模型和规模报酬可变(VRS)特征的BBC模型。然而,传统DEA模型是基于自身最优权重向量的自评DEA,也可能会出现多个评价单元效率同时有效等情况。

为了克服传统DEA方法的缺陷,学者们进行了理论与方法创新。Anderson等建立了超效率DEA模型来解决有效决策单元的排序问题[2]。Tone创建了包含松弛变量的非径向、非角度的SBM模型,以消除冗余投入对效率值准确性的影响[3]。随后,Tone进一步提出超效率SBM模型,解决了多个有效决策单元的排序问题[4]。Sexton等提出了DEA交叉效率评价方法,它是基于一组公共权重向量集的互评DEA,可以实现决策单元全排序[5]。程幼明等基于群决策理论,分析属性偏好及其属性效用变化特征,采用熵权法研究属性效用稳定性,提出了考虑属性效用一致性的DEA他评交叉公共权重评价法[6]。龚日朝等将DEMATEL方法和DEA方法相结合,运用DEMATEL法确定指标权重大小,纳入DEA非阿基米德无穷小量ε限制的CCR模型及其超效率模型的约束条件,建立了权重约束型ε-CCR模型、超效率ε-CCR模型[7]。

关于DEA方法的理论研究不断深入,DEA模型被不断地改进。Seiford等通过将盈利能力和市场性分开形成两阶段的生产过程,利用数据包络分析方法考察了美国前55家商业银行的绩效[8]。Fried等创建了三阶段DEA模型,它能修正环境变量和随机误差的影响,使研究对象效率评价更为准确[9]。Kao等提出了两阶段关联DEA模型,它考虑了两个子过程在整个过程中的序列关系,并将整个过程的效率分解为两个子过程效率的乘积[10]。Wang等发展了两阶段DEA模型,采用加权调和平均数方法得到两个阶段的综合效率,并将Kao等的模型推广到规模报酬可变假定[11]。

已有DEA方法的研究和应用主要集中于截面DEA和面板DEA,时间序列DEA模型的研究和应用较少。Lynde等提出一个时间序列DEA模型,并用该模型研究1966—1990年英国制造业生产率与效率的变化[12]。王兵等应用Lynde和Richmond的时间序列DEA模型实证研究了中国1952—2000年生产率与效率的波动情况[13]。赵当如等也应用该模型测度了湖北省1997—2014年财政科技投入效率[14]。秦钟等应用DEA时间窗分析法研究了广东省21个地市1994—2007年农业投入产出的效率,且从横向与纵向两个方面就各地市农业发展的相对效率以及变化趋势进行对比分析[15]。目前的时间序列DEA模型基于评价目标的投入产出时间序列数据考察技术进步,由于信息不足,对包括效率在内的一些指标的估算只是给出了上下边界值,开发能够准确估计效率值的时间序列DEA模型是需要进一步研究的方向。

虽然现有DEA方法通过投入、产出数据直接测算得到评价对象的效率值,具有利用较少数据得到较好的评价结果的优点。但是,当已经知道或容易获得关于评价对象其他有用信息的情况下,如果还仅仅只是利用投入产出数据对评价对象的效率进行测算,那么将没有充分利用有效信息来进一步提升评价的效果。比如,在现实世界中,有些情况下单一评价对象在不同时点的技术进步或不同评价对象集合在不同时点的技术进步是已知或容易获得的。此时,如果不充分利用这些关于技术进步状况的信息,那么采用DEA方法来计算评价对象的效率将不够准确,甚至导致所得效率值或据此作出的决策大大偏离实际。

因此,本文以技术进步作为切入点,讨论此时评价对象的效率测度问题。对技术进步的DEA模型的研究包含四个方面:一是单一评价对象自身在不同时点存在的技术进步;二是评价对象集合自身在不同时点存在的技术进步;三是在某一时点社会的最高技术水平相对于该时点上不同评价对象集合而言存在的技术进步;四是在某一时点社会的最高技术水平相对于该时点上单一评价对象而言存在的技术进步。当存在上述四个方面的技术进步时,若采用DEA进行效率评价,应将技术进步因素考虑在内,否则将难以准确衡量评价对象的实际效率。考虑技术进步的效率指的是单位技术水平(标准量)下的产出与投入之比,它反映了在特定的技术水平下得到一定的产出是否使用了最少的投入。本文以具有规模报酬不变特征的CCR、SE-CCR模型以及规模报酬可变特征的BCC、SE-BCC模型为例,分析技术进步对评价对象效率值的影响。与以往研究不同的是,将技术进步由评价对象的投入产出测算得到(“内生”),变为由外部给定或测算得到(“外生”),从而克服已有DEA模型的缺陷,扩大DEA模型的应用范围。

图1 考虑评价对象技术进步的时间序列DEA模型效率分析

二、考虑评价对象技术进步的时间序列DEA模型

如果单一评价对象在不同时点不存在技术进步,那么对其在不同时点的效率进行评价时测算方法与截面DEA相同。单一评价对象自身在不同时点往往存在着技术进步,可能是有的时点存在技术进步,或者是不同时点都存在技术进步。若根据不同时点投入产出的情况构造生产前沿面,而不考虑技术水平的变化,那么测算出来的效率值将是错误的。因为此时出现了上述第一种情形的技术进步,即单一评价对象自身在不同时点存在技术进步。

如图1所示,图中是单一评价对象5个不同时点(A、B、C、D和E)的投入产出情况,它们均有两项投入x1与x2以及1项产出y,横轴为单位产出的x1投入数量,纵轴为单位产出的x2投入数量。由于该对象除了A时点外的4个时点存在技术进步(图中假设这4个时点均有技术进步),它们的原始投入经过技术进步转换后的投入(简称“转换后投入”)分别是B′、C′、D′和E′,与各自的原始投入相比都变大了。此时,剔除技术进步影响的效率评价单元为:A、B′(对应B时点)、C′(对应C时点)、D′(对应D时点)和E′(对应E时点)。第一,根据这5个时点的数据得到标准的DEA模型,因为技术进步原有的生产前沿面发生了变化,C′、E′、D′形成了新的有效生产前沿面,因此它们(分别对应C、E和D)的效率均为1(OC′/OC′、OE′/OE′、OD′/OD′),而A、B′(对应B)的效率(OA01/OA、OB01/OB′)都小于1。第二,根据这5个时点的数据得到超效率的DEA模型,在计算该评价对象某个时点效率时,其他时点形成有效的生产前沿面。例如,对E′来说它不再位于前沿面上,前沿面只包括C′和D′,E′的投影点在E*,E′(对应E)的效率为OE*/OE′(大于1)。原来没有处于前沿面上的时点效率不变(与标准的DEA模型相同),如A、B′(对应B)。此外,在上述两种类型的DEA模型中,规模报酬变化带来的影响是前沿面的形状及其移动距离的大小,如CED到C′E′D′、CD到C′D′之间的距离。

假设要对某单一评价对象(地区或企业等)的n个时点(年或月等)DMU{DMUj:j=1,2,…,n}进行评价:它利用m种投入xcj(c=1,2,…,m)生产s种产出yrj(r=1,2,…,s),该评价对象在j时点的技术水平为kj(k1=1,kj为相对于k1的标准量),当时社会的最高技术水平为kj0(kj0=kj)。那么根据考虑技术进步的效率含义,第一种情形的技术进步(kj*≥kj*-1,kn>k1,j*=2,…,n)对评价对象效率值的影响分析如下:

(一)CCR模型(同一对象不同时点)

考虑评价对象技术进步的时间序列CCR模型为:

(1)

(2)

(3)

令vTxiki=1,则可将式(2)写成如下形式:

(4)

则式(4)的对偶形式为:

(5)

(6)

(二)SE-CCR模型(同一对象不同时点)

考虑评价对象技术进步的时间序列SE-CCR模型为:

(7)

同理,可以得到式(7)的对偶形式为:

(8)

(9)

(三)BCC模型(同一对象不同时点)

考虑评价对象技术进步的时间序列BCC模型为:

(10)

(11)

(12)

令vTxiki=1,则可将式(11)写成如下形式:

(13)

则式(13)的对偶形式为:

(14)

(15)

(四)SE-BCC模型(同一对象不同时点)

考虑评价对象技术进步的时间序列SE-BCC模型为:

(16)

同理,可以得到式(16)的对偶形式为:

(17)

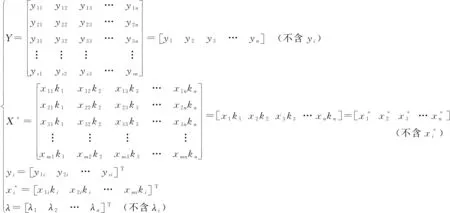
(18)

从CCR、SE-CCR、BCC、SE-BCC模型来看,第一种情形的技术进步(kj*≥kj*-1,kn>k1,j*=2,…,n)对评价对象效率值的影响体现在改变了评价的投入参考数值,该对象的不同时点的投入均乘以该时点的技术水平。与不考虑评价对象技术水平相比,计算得到的相对效率值发生了变化,所得效率值等于其真实效率值,投入的实际冗余值为原来的1/ki。这就是说在评价对象按实际冗余值进行投入调整后得到同样产出的情况下,其实际效率值可达到最大。

图2 考虑评价对象技术进步的面板DEA模型效率分析

三、考虑评价对象技术进步的面板DEA模型

同样,如果评价对象集合自身在不同时点均不存在技术进步,那么对其在不同时点的效率进行评价时测算方法与截面DEA相同。但评价对象集合自身在不同时点往往也存在着技术进步,可能是有的时点存在技术进步,或者是不同时点都存在技术进步。若根据不同时点投入产出的情况构造生产前沿面,而不考虑技术水平的变化,那么测算出来的效率值也将是错误的。因为此时出现了上述第二种情形的技术进步,即评价对象集合自身在不同时点存在技术进步。

如图2所示,图中是5个评价对象(A0、B0、C0、D0和E0)两个不同时点的投入产出情况,分别是A、B、C、D、E(时点1),以及A′、B′、C′、D′和E′(时点2),它们均有两项投入x1与x2以及1项产出y,横轴为单位产出的x1投入数量,纵轴为单位产出的x2投入数量。由于评价对象集合在时点2(A′、B′、C′、D′和E′)存在技术进步,它们的“转换后投入”分别是A*、B*、C*、D*和E*,与各自的原始投入相比都变大了。

(1)根据A、B、C、D、E、A′、B′、C′、D′和E′数据得到标准的DEA模型,因为技术进步原有的生产前沿面发生了变化,C、E*、B*、D形成了新的有效生产前沿面,因此它们(分别是C、E、B、D)的效率均为1(OC/OC、OE*/OE*、OB*/OB*、OD/OD),而A、B、E、A′、C′、D′的效率都小于1。

(2)根据A、B、C、D、E、A′、B′、C′、D′和E′数据得到超效率的DEA模型,在计算给定评价对象某个时点效率时,该评价对象其它时点或其它评价对象各时点形成有效的生产前沿面。例如,对于E*(对应E′)来说它不再位于前沿面上,前沿面只包括C和B*,E*的投影点在E**,E*(对应E′)的效率为OE**/OE*(大于1);而原来没有处于前沿面上的A、B、E、A′、C′、D′效率不变(与标准的DEA模型相同)。此外,在上述两种类型的DEA模型中,规模报酬是否变化带来的影响是前沿面的形状及其包含范围的变化,如CE′B′D到CE*B*D、CB′D到CB*D之间的变动。更多评价对象更多时点的效率的评价以此类推。

假设要对n个评价对象(地区或企业等)的T0个时点(年或月等)DMU{DMUjt:j=1,2,…,n;t=1,2,…,T0}进行评价:它利用m种投入xcjt(c=1,2,…,m)生产s种产出yrjt(r=1,2,…,s),这些评价对象在t时点的最高技术水平为kt(k1=1,kt为相对于k1的标准量),当时社会的最高技术水平为kt*(kt*=kt)。那么根据考虑技术进步的效率含义,第二种情形的技术进步(kt′≥kt′-1,kn>k1,t′=2,…,n)对评价对象效率值的影响分析如下:

(一)CCR模型(不同对象不同时点)

考虑评价对象技术进步的面板CCR模型为:

(19)

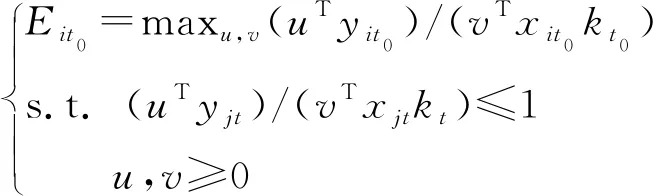
(20)

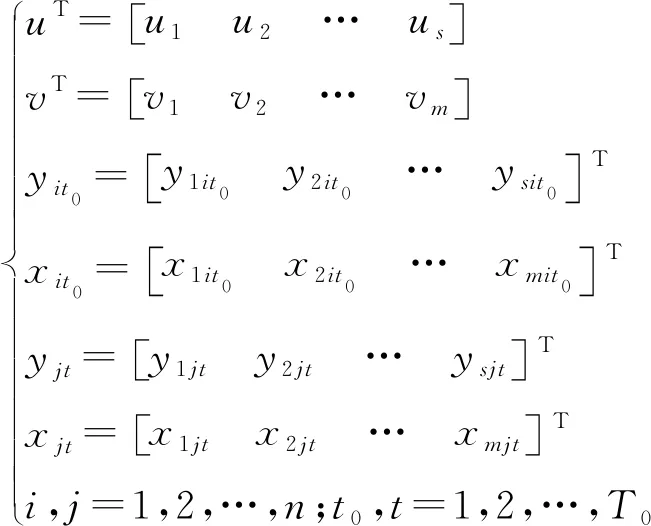
(21)

令vTxit0kt0=1,则可将式(20)写成如下形式:

(22)

则式(22)的对偶形式为:

(23)

其中,

(24)

(二)SE-CCR模型(不同对象不同时点)

考虑评价对象技术进步的面板SE-CCR模型为:

(25)

同理,可以得到式(25)的对偶问题为:

(26)

其中,

(27)

(三)BCC模型(不同对象不同时点)

考虑评价对象技术进步的面板BCC模型为:

(28)

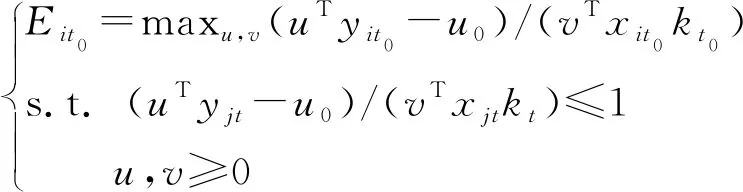
(29)

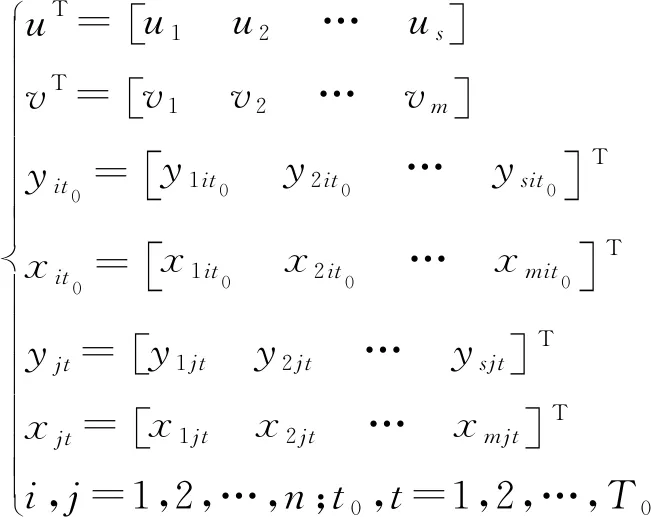
(30)

令vTxit0kt0=1,则可将式(29)写成如下形式:

(31)

则式(31)的对偶形式为:

(32)

其中,

(33)

(四)SE-BCC模型(不同对象不同时点)

考虑评价对象技术进步的面板SE-BCC模型为:

(34)

同理,可以得到式(34)的对偶问题为:

(35)

其中,

(36)

从CCR、SE-CCR、BCC、SE-BCC模型来看,第二种情形的技术进步(kt′≥kt′-1,kn>k1,t′=2,…,n)对评价对象效率值的影响与第一种情形的技术进步类似,体现在改变了评价的投入参考数值,各评价对象的不同时点的投入均乘以该时点的技术水平。与不考虑评价对象集合自身技术水平相比,相对效率值发生了变化,计算得到的效率值等于其真实效率值,投入的实际冗余值为原来的1/kt0。这就是说在评价对象按实际冗余值进行投入调整后得到同样产出的情况下,其实际效率值可达到最大。

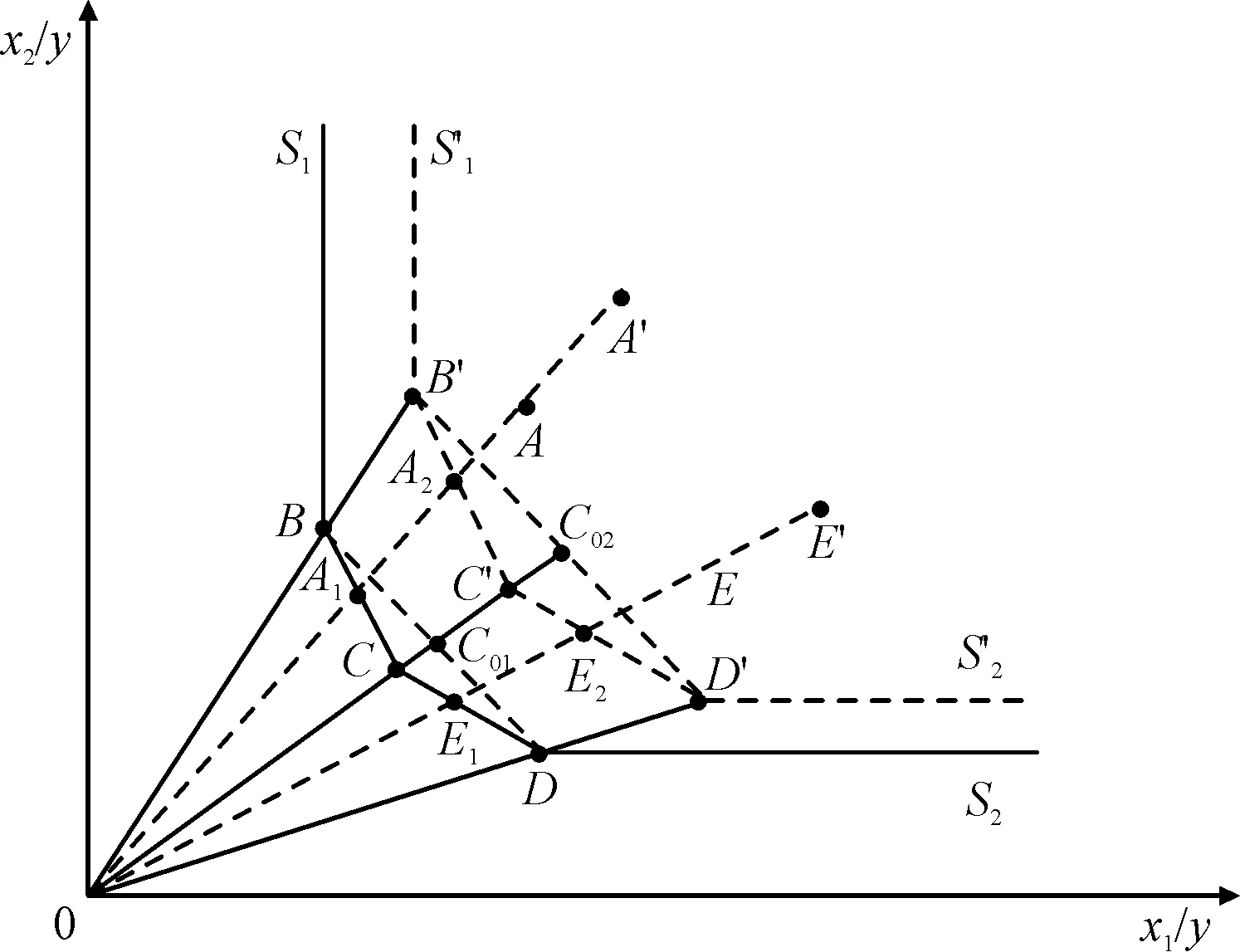
图3 考虑当时社会技术进步的截面DEA模型效率分析

四、考虑当时社会技术进步的截面DEA模型

目前的截面DEA模型在进行效率评价时,根据不同评价对象投入产出的情况,构造有效的生产前沿面反映它们的技术水平,并不考虑该技术水平相对于当时社会的最高技术水平的大小。因此,测算出来的效率值并不一定是当时评价对象的实际效率值,而是不同评价对象之间的相对效率值。因为此时出现了上述第三种情形的技术进步,即在某一时点社会的最高技术水平相对于该时点上不同评价对象集合而言存在技术进步。只有在根据不同评价对象构造的生产前沿面包含了当时社会的最高技术水平的生产可能性曲线的时候,它们之间的相对效率值才等于其实际效率值。

如图3所示,图中有5个评价对象(A、B、C、D和E),它们均有两项投入x1与x2以及1项产出y,横轴为单位产出的x1投入数量,纵轴为单位产出的x2投入数量。

(1)根据5个评价对象数据得到标准的DEA模型,B、C、D这3个评价对象形成了有效的生产前沿面,因此它们的效率均为1(OB/OB、OC/OC、OD/OD),而A、E的效率(OA1/OA、OE1/OE)都小于1。若社会的最高技术水平高于5个评价对象集合,那么5个评价对象的实际效率值将变得更小。它们的“转换后投入”分别是A′、B′、C′、D′和E′,与各自的原始投入相比都同比例(乘以k)变大了。此时,有效生产前沿面为B′C′D′,A、B、C、D、E的相对效率值大小不变,分别是OA2/OA′、OB′/OB′、OC′/OC′、OD′/OD′、OE2/OE′,对应技术水平是k,实际效率值分别是它们的1/k。(2)根据5个评价对象数据得到超效率的DEA模型,在计算某个评价对象效率时,其他评价对象形成有效的生产前沿面。例如,对于C来说它不再位于前沿面上,前沿面只包括B和D,C的投影点在C01,评价对象C的效率为OC01/OC,而原来没有处于前沿面上的评价对象的效率不变(如A、E)。若社会的最高技术水平高于5个评价对象集合,那么5个评价对象的实际效率值同样将变得更小。对于C′(对应C)来说,前沿面变为B′D′,C′的投影点在C02,评价对象C的相对效率值为OC02/OC′(大小保持不变),对应的技术水平是k,实际效率值是它的1/k;而原来没有处于前沿面上的评价对象的相对效率不变(与标准的DEA模型相同),如A′(对应A)、E′(对应E),实际效率同样是它的1/k。其它评价对象以此类推。此外,在上述两种类型的DEA模型中,规模报酬是否变化带来的影响是前沿面的形状及其移动距离的大小,如BCD到B′C′D′、BD到B′D′之间的距离。综上所述,即使社会技术水平高于评价对象集合的技术水平,也并不会改变同一时点既定评价对象的相对效率值,但会使评价对象的实际效率值变小。

假设有n个评价对象(地区或企业等)DMU{DMUj:j=1,2,…,n},利用m种投入xcj(c=1,2,…,m)生产s种产出yrj(r=1,2,…,s),这些评价对象的最高技术水平为k0(k0=1),当时社会的最高技术水平为k(k为相对于k0的标准量)。那么根据考虑技术进步的效率含义,第三种情形的技术进步(k>1)对评价对象i(i=1,2,…,n)效率值的影响分析如下:

(一)CCR模型(同一时点不同对象)

考虑社会技术进步的CCR模型为:

(37)

(38)

(39)

令vTxi=1,则可将式(38)写成如下形式:

(40)

则式(40)的对偶形式为:

(41)

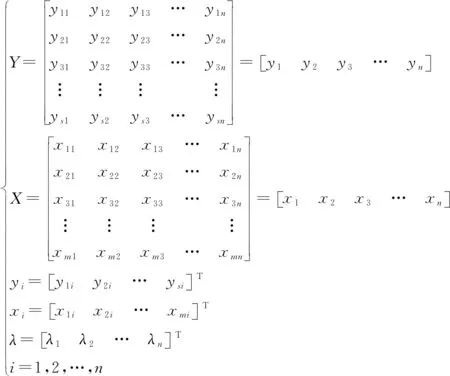
(42)

(二)SE-CCR模型(同一时点不同对象)

考虑社会技术进步的SE-CCR模型为:

(43)

同理,可以得到式(43)的对偶形式为:

(44)

(45)

(三)BCC模型(同一时点不同对象)

考虑社会技术进步的BCC模型为:

(46)

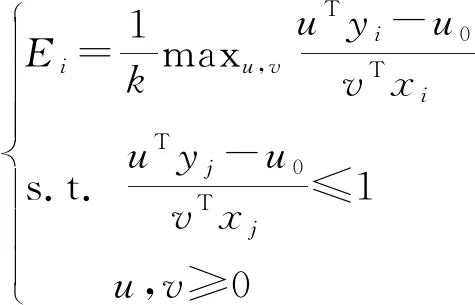
(47)

(48)

令vTxi=1,则可将式(47)写成如下形式:

(49)

则式(49)的对偶形式为:

(50)

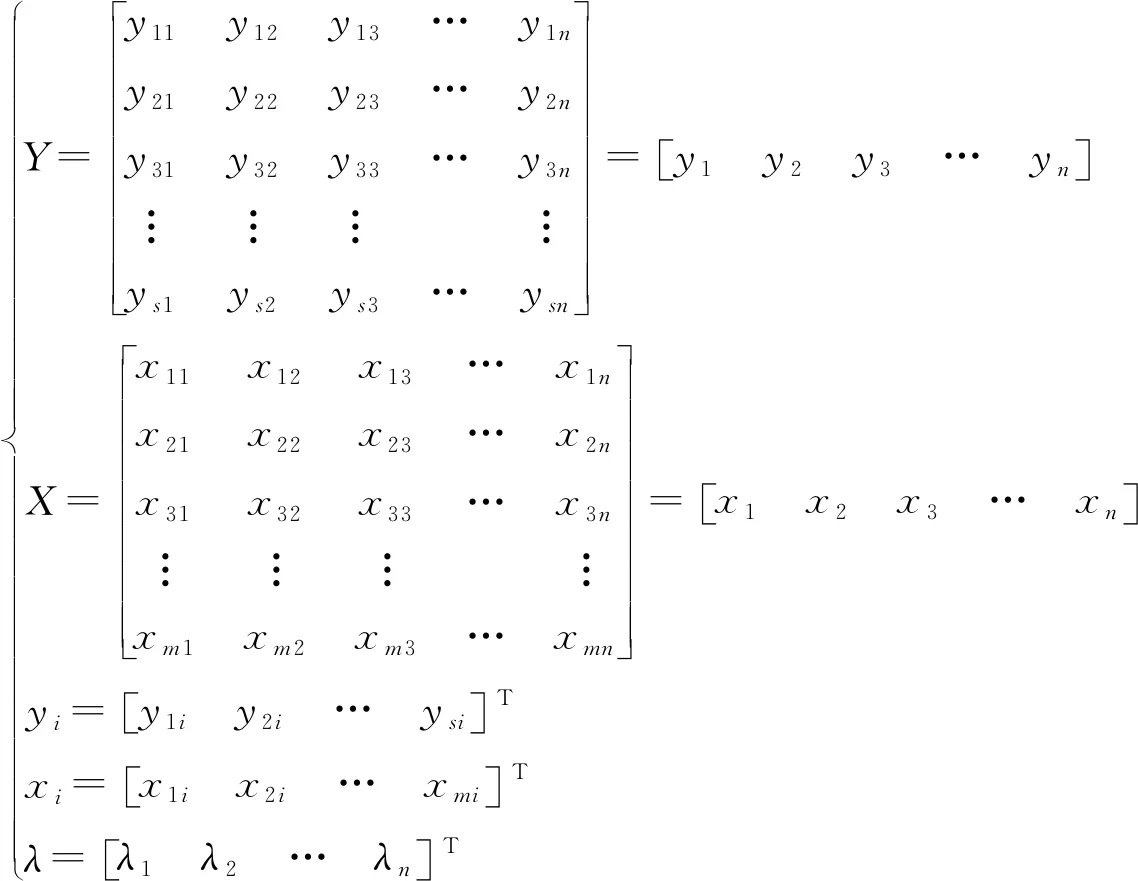
(51)

(四)SE-BCC模型(同一时点不同对象)

考虑社会技术进步的SE-BCC模型为:

(52)

同理,可以得到式(52)的对偶形式为:

(53)

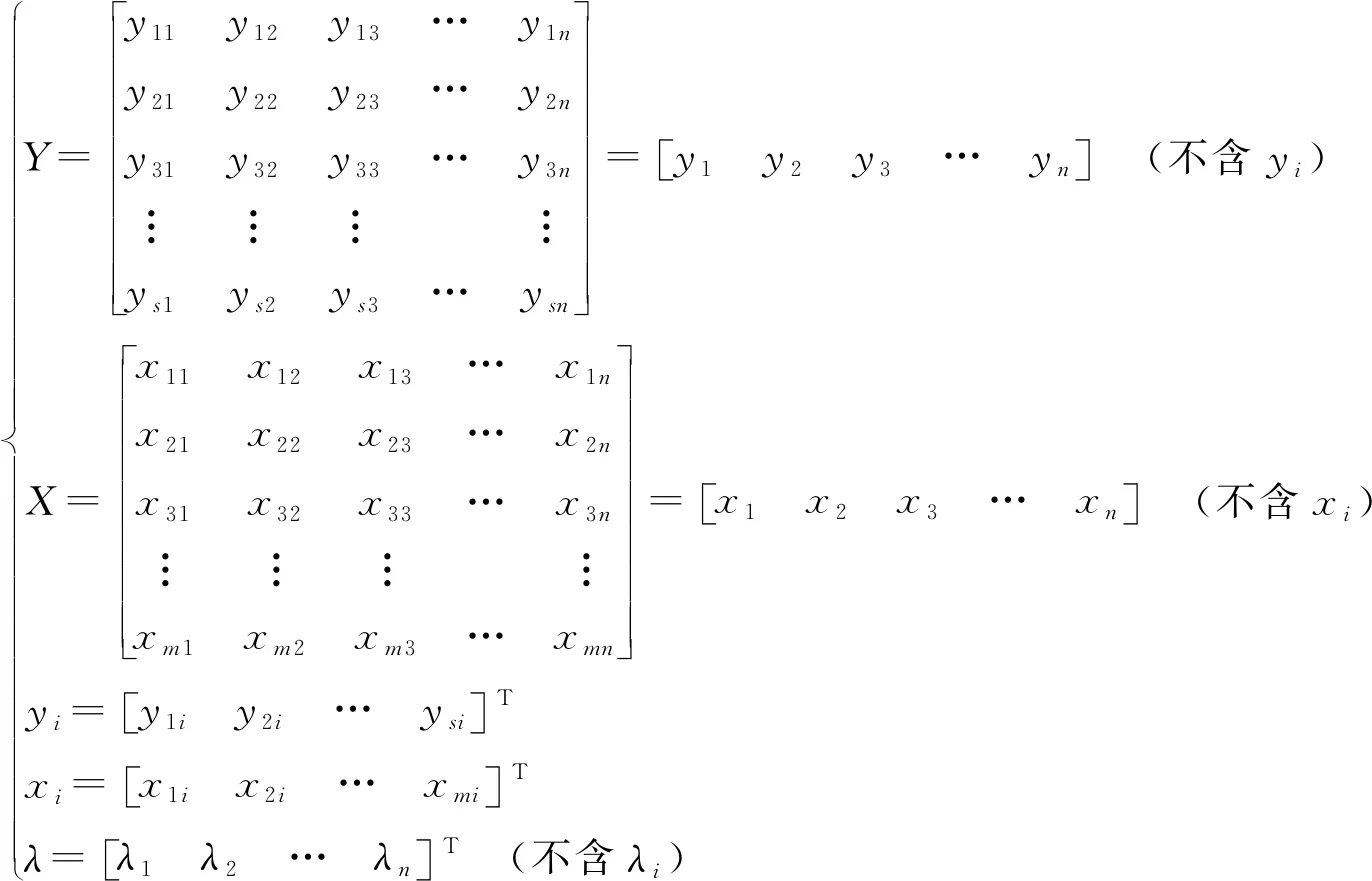
(54)

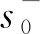
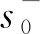
五、结论

考虑技术进步的DEA方法,将技术进步由评价对象的投入产出测算得到(“内生”),变为由外部给定或测算得到(“外生”)。对于评价对象或社会存在技术进步的情形,通过引入“转换后投入”,使同一时点不同评价对象、单一评价对象不同时点、不同评价对象不同时点的投入产出比较位于同一标准,并对标社会技术水平。从而克服已有DEA模型的缺陷,扩大DEA模型的应用范围。从CCR、SE-CCR、BCC、SE-BCC模型来看,相比之下考虑技术进步的DEA方法的操作处理同样也比较简单,只需对投入或效率的计算稍作变动。下面分别对在几种不同类型的技术进步情况下效率的计算及其结果的处理总结如下:

(1)单一评价对象自身在不同时点存在技术进步,在计算或软件输入时只需将该对象的不同时点的投入均乘以该时点的技术水平,并按原有方法进行计算。求得的效率值便是所需要的真实效率值,得到的投入冗余值乘以1/ki(ki为评价对象在该时点的技术水平)便是所需要的投入实际冗余值。

(2)评价对象集合自身在不同时点存在技术进步,在计算或软件输入时只需将各评价对象的不同时点的投入均乘以该时点的技术水平,并按原有方法进行计算。求得的效率值便是所需要的真实效率值,得到的投入冗余值乘以1/kt0(kt0为评价对象集合在该时点的最高技术水平)便是所需要的投入实际冗余值。

(3)在某一时点社会的最高技术水平相对于该时点上不同评价对象集合而言存在技术进步,将得到的相对效率值乘以1/k(k为当时社会的最高技术水平)就可得到评价对象的真实效率值,得到的投入目标值的(1-1/k)与投入冗余值相加,就可得到评价对象的投入实际冗余值。

(4)在某一时点社会的最高技术水平相对于该时点上单一评价对象而言存在技术进步,且单一评价对象自身在不同时点也存在技术进步,只需将该对象的不同时点的投入均同时乘以该时点该评价对象的技术水平kj,并按原有方法进行计算。所得效率值的1/kj0即为其真实效率值,投入的实际冗余值可由投入冗余值s-乘以1/kj之积、投入目标值x乘以(1-1/kj0)×1/kj之积二者求和得到(kj0是相对于kj的标准量,表示当时社会的最高技术水平)。

(5)在某一时点社会的最高技术水平相对于该时点上不同评价对象集合而言存在技术进步,且评价对象集合自身在不同时点存在技术进步,只需将不同评价对象的不同时点的投入均乘以这些评价对象该时点的最高技术水平kt,并按原有方法进行计算。所得效率值的1/kt*等于其真实效率值,投入的实际冗余值可由投入冗余值s-乘以1/kt之积、投入目标值x乘以(1-1/kt*)×1/kt之积二者求和得到(kt*是相对于kt的标准量,表示当时社会的最高技术水平)。

综上所述,考虑技术进步的DEA方法,容易理解,计算操作简便,具有较大的应用价值。该方法一方面能够充分利用已有信息,提升评价准确性;另一方面能够扩大该方法的应用范围,有助于解决现实问题。