关于含顺序类别解释变量的Logistic回归模型研究
2021-03-17谭雨昕
晁 越,谭雨昕,许 丹,黄 磊
(1.西南交通大学 数学学院,四川 成都 611756;2.西南财经大学 统计学院,四川 成都 611130;3.爱思瑟国际学校,四川 成都 611731)
一、引言
回归分析的应用十分广泛,其中关于响应变量是类别变量和计数变量的模型研究是回归分析中的重要课题之一。根据回归模型类别响应变量的类型来看,当响应变量为二元变量时,现已成熟并且被广泛运用的回归模型有Logistic回归模型和Probit回归模型[1-2];当响应变量为多类别变量(Multiple Categorical Variables)时,Ordered Logit模型和Multinomial Logit回归模型分别被运用于顺序类别响应变量和无序类别响应变量的场合[3-5]。另一种离散取值的响应变量为计数响应变量,对数线性模型可以对计数响应变量进行列联表分析(频数交叉列联表),从而估计出解释变量对响应变量条件分布的影响程度[6]。
综上所述,关于类别响应变量的回归分析研究和方法已日趋成熟,其中关于顺序类别响应变量的研究与应用也不胜枚举。然而,在医学研究和其他众多交叉学科研究的实际问题中,研究者们所构建的回归模型时常会包含顺序类别解释变量(Ordinal Multinomial协变量,OM协变量或OM解释变量)。例如,在一项对患者生活方式的调查中,考察患者的吸烟状况类别(每天几支烟、每天一包、每天两包、每天两包以上),类似的以酒精消耗情况作为OM解释变量的例子也可以找到[7]。除此之外,很多不同病况下的患者也往往表现为重度损伤、轻度损伤、正常或非常好[8]。又如,在某项国民教育的研究中,受教育的水平可以分为小学、中学、大学和研究生教育[9]。
虽然在实际问题中OM解释变量经常出现,但据我们所知,仅有很少的统计学者从理论上系统地研究过包含OM解释变量的回归模型,且他们的研究成果在理论上存在一定的局限性,在处理实际问题时又缺乏适应性。早期,Walter等发表的一篇文章开创性地研究含有OM解释变量的回归模型,提出了一种针对OM解释变量的编码方案,把这种编码方案运用于回归模型时,能够很好地解释估计的参数[10]。然而,该方法仅用OM解释变量的秩序尺度水平对估计出来的参数进行解释,仍面临估计值过拟合和不存在等问题,尤其当模型的OM解释变量很多时,更是扩大了上述问题的严重性。另一方面,有的学者为了避免采用哑变量解决此类回归问题,更偏向于将OM解释变量直接当作连续型变量,将适用于连续型变量的回归分析方法直接应用到含OM解释变量的回归问题当中[11]。这种将OM解释变量视为连续变量的一个严重问题是不得不预先对一些OM解释变量进行主观赋值。因此,当这些类别实际表示诸如“强烈同意”“轻微同意”“中立”“轻微反对”“强烈反对”等定性判断时,对于这些OM解释变量进行主观的赋值是不合理的,因为一旦考虑对回归系数作解释,不同的主观数值就会对解释变量的效应产生不同的结论。
为了处理含OM解释变量的回归问题,研究人员已经提出了一些有效可行的办法。Gertheiss等提出了一种运用岭回归的处理方法,最终得到了参数的稳健性估计[12]。但是用基于范数惩罚的岭回归估计仍然存在估计偏差,并且在OM解释变量含有伪分类(某相邻两类无差别可合并)的情形下依然会产生过拟合的现象。刘赛可等提出基于Fisher精确检验准则、CACM和ACACM准则的多类别变量类合并方法对多类别变量进行预处理,再对处理后的数据进行Logistic回归建模[13]。但是该方法的局限性在于只考虑了模型中含有1个多类别变量的类合并方法且未对伪分类合并的相合性进行研究。对于含多个类别变量的情形,Tian等结合Walter等提出的关于哑变量的编码方案和Gertheiss等提出的惩罚估计方法,提出了一种简单的哑变量线性变换方法来处理含OM解释变量的线性回归模型[10,12,14]。
由于BIC准则具有模型选择的相合性,可有效地避免过拟合现象[15-17]。Tian等将所提出的哑变量线性变换与BIC准则相结合,以筛选线性回归模型中OM解释变量的伪分类[15]。但是,在一些实际问题的研究中,尤其是在生物医学领域,往往还会遇到响应变量Y=0,1且含OM解释变量的广义线性回归模型,其响应变量不连续,它们有可能是二元变量或者是计数型的数据等。Tian等提出的筛选线性回归模型中OM解释变量的伪分类方法就不再适用[14]。本文基于医学统计中最常见的广义线性模型——Logistic模型,考虑OM解释变量的存在,并对所提出的伪分类筛选方法进行研究,并将继续采用BIC筛选准则与哑变量线性变换相结合的方法对伪分类进行筛选。与Tian等提出的TD-BIC方法不同的是,当模型中含有OM解释变量时,Logistic模型运用似然方程的迭代加权最小二乘解法求解模型的系数,与线性模型的最小二乘法有显著区别,此外,本文还探究了LTD-BIC方法相关估计量渐近性质的前提条件[14]。文中给出的基于一些正则化条件的定理和引理,其证明方法和所用技巧相对于线性模型也有所不同,在一定程度上添补了研究空白。除此之外,在模拟过程中,通过对比多个模型考察LTD-BIC方法在含有多个OM解释变量情形下是否具有局限性,并确定OM解释变量中的类别数量对筛选结果是否有影响。本文所提出的方法便于用统计软件R和SAS实现。
二、模型与方法
本节首先介绍包含OM解释变量的Logistic回归模型,然后提出针对该模型的OM解释变量中含有伪分类的筛选方法——LTD-BIC方法和算法,最后证明了通过LTD-BIC方法筛选OM解释变量中的伪分类后得到的模型具有相合性。
(一)模型描述
在以下模型推导中仅考虑包含一个OM解释变量X*的Logistic回归模型,而实际问题中的模型可包含多个OM解释变量,可仅需对本文提出的方法简易推广。假设X*具有k个类别(k≥2),记X2,…,Xk为其k-1个哑变量。服从伯努利分布的二元响应变量Yn=1的概率Pn可以由如下Logistic回归模型表示:
(1)
在一些医学等实际问题的研究中,研究人员还需要考虑一些连续型解释变量与OM解释变量共同存在的Logistic模型。为了使模型更加符合实际问题的研究,本文在模型(1)加入了连续型解释变量{Zj,j=1,2,…,p}。X*的第k个哑变量Xk的第n个分量Xk,n定义为:
(2)
根据哑变量的编码方案,对于有k个类别的OM解释变量X*,取第一类为基准类别,剩余的k-1类为比较类别。因此,α代表当其余解释变量取值为0时,在OM解释变量X*为第一类别的影响下Yn=1的概率Pn的Logit值,β2代表当其余解释变量不变时,在X*为第一个类别和第二个类别时Yn=1的概率Pn的Logit值之差,{β3,…,βk}有类似的解释意义。
令Y是由所有服从两点分布的响应变量组成的向量,将模型(1)改为矩阵形式
Q=Xβ
(3)
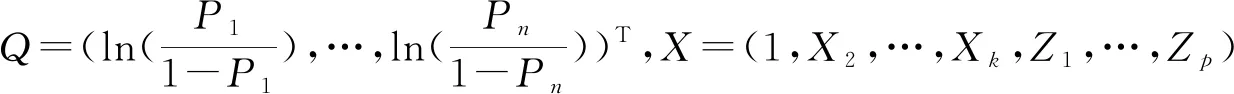
(二)LTD-BIC方法
研究思路来源于Gertheiss和Tutz曾提出一种改良后的对于包含OM解释变量线性模型的岭回归分析,其所要处理的回归模型并没有包含连续型解释变量的情况[12],模型为:
Yi=α+β2X2,i+…+βkXk,i+εi
(4)
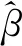
(5)
其中,令β1=0。岭回归是一种广义最小二乘估计,常常用于估计自变量高度线性相关时简单线性回归模型的参数,而在式(5)改良后的岭回归中,Gertheiss和Tutz是通过L2范数惩罚了相邻两个类别的系数之差。本文希望响应变量Y能够在X*的相邻类别之间缓慢变化,即避免类别之间发生大的跳跃,倾向于构造出一个平滑系数向量。但Gertheiss和Tutz的方法仍然不能解决包含OM解释变量的回归模型过拟合问题。也就是说,该方法不能筛选出OM解释变量中的伪分类。本文定义相邻两个类别的系数之差为Δβj=βj-βj-1。基于文献[14]中又提出的一种改进方法,将继续采用简单的哑变量线性变换与BIC准则相结合的方法来“探测”出系数之差Δβj(j=2,…,k)为0的解释变量,同时称βj为一个伪分类。接下来给出LTD-BIC算法的四个主要步骤:
LTD-BIC算法
Step1 首先,将式(3)改写为如下等价关系式:
(6)
Step2 将式(6)中相同的相邻系数之差的哑变量组合在一起,得到以下模型:
(7)
(8)

以下将证明,通过运用LTD-BIC方法筛选到伪分类的正确率随着样本量趋近于无穷时是依概率收敛到1的。将模型(8)改写为矩阵的形式:
Q=X*β
(9)
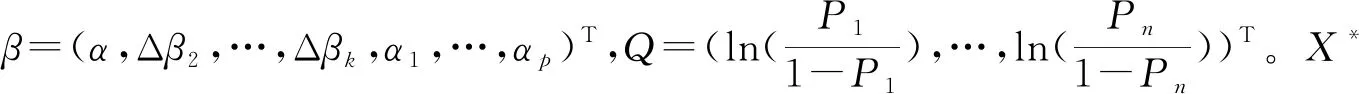
其中,1-j=1{X*≠s,1≤s≤j}是一个取值为0或1的示性函数,表示对于所有的s∈{t:1≤t≤j},当X*≠s时1-j取值为1,否则取值为0。已知模型(8)的对数似然函数可以表示为:
(10)
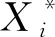
(11)

βnew=(X*TWX*)-1X*TWZ
Z=βoldTX*+W-1(Y-p)
(12)
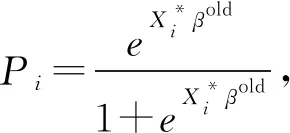
(三)LTD-BIC的相合性
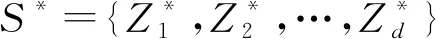
当样本量为N时,定义由LTD-BIC方法筛选出来的解释变量所组成的集合为SN:
(13)
令Fisher信息矩阵为:
(14)
为证明LTD-BIC的相合性,需要以下正则化条件:
A1:OM解释变量X*与其它连续型解释变量Z1,Z2.…,Zp是相互独立的;
A2:设总样本量大小为N,OM解释变量{X*=j,j=1,…,k}的每一个类别的样本量的大小分别为n1,n2,…,nk,第j个类别的指标集为Inj,并设n(1)和n(k)分别为所有类别中样本量的最大值和最小值,假设
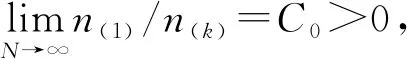

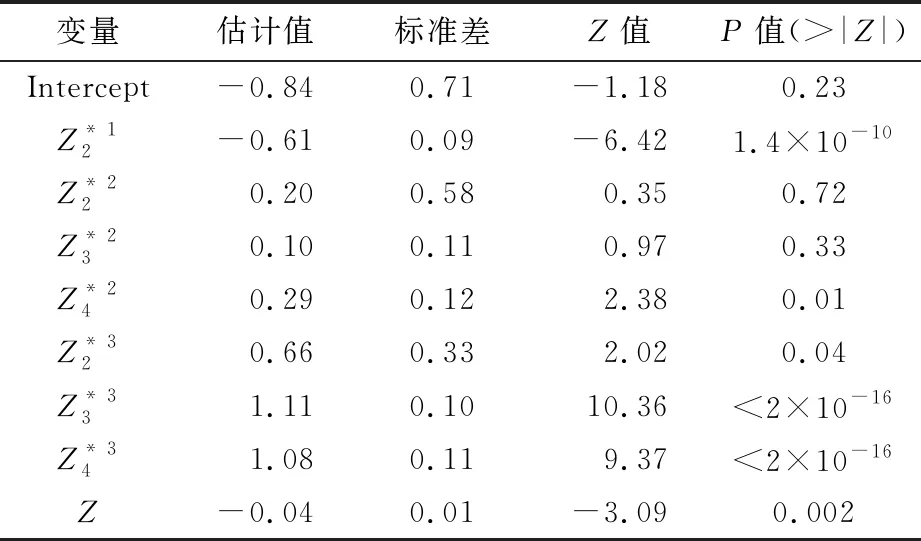
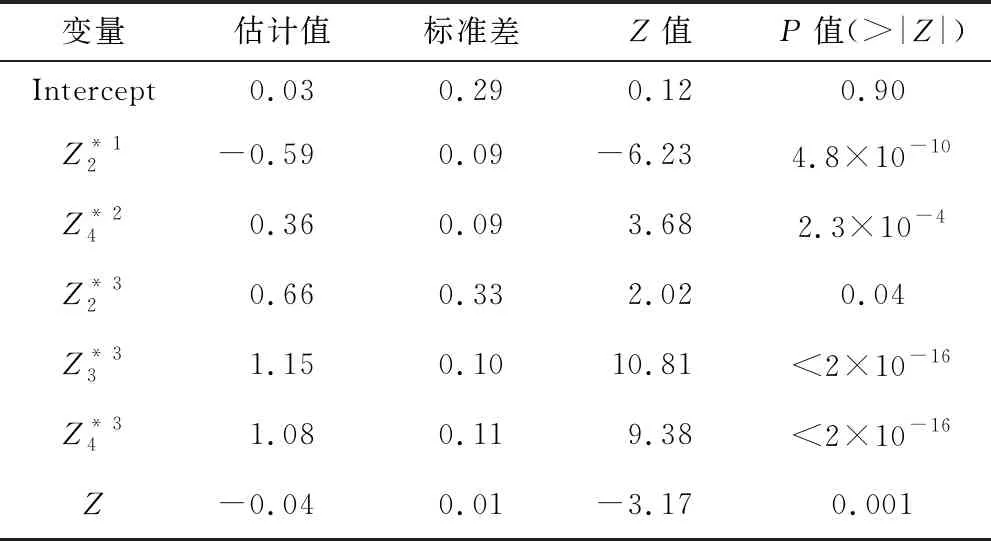
A4:对于任意的ε>0,设β*满足‖β*-β0‖≥ε,其中β0为模型(9)的真实系数向量,则存在α>1和0 注记1条件A2表明,由于哑变量为离散型变量,为了消除对于OM解释变量中不同类别之间的相互影响(多重共线性),假设当样本量无穷大时,存在最小样本量的类别和最大样本量的类别样本量之比大于0的常数,保证了下面的引理1成立。 引理1根据条件A1~A3,对于模型(9),Fisher信息矩阵(14)是正定的。 (15) 对于矩阵(15),可以找到一个非奇异矩阵D: (16) 使得 (17) 对式(17)求极限: (18) 由条件A2可知, 同样可以找到一个非奇异矩阵H, 使得, 其中,Ⅱk和Ⅱp分别为k阶和p阶单位矩阵。因此,由条件A3可知Σ0是一个正定矩阵。 引理1保证了模型(9)的回归系数β的Fisher信息矩阵是一个正定矩阵,从而使得β可由似然方程的迭代最小二乘法估计;同时也保证了定理1的证明。最后,所选出的模型满足下面的相合性统计性质: (19) 证明:当SN≠S0时, (20) (1)考虑欠拟合的情况。当SNS0时,PSN (21) 由此可得,式(20)成立。 (2)考虑过拟合的情况。当S0SN时,有PSN=PS0,考虑如下假设检验问题, 对于对数似然比统计量: 由引理1可知,在H0成立的情况下,统计量Λ是渐近服从于卡方分布的。所以有 (22) (3)当SN∩S0≠S0且SN∩S0≠SN时,令SN∩S0=S#,则S#⊂SN且S#⊂S0。由Wilks定理和条件A2可知, (23) 以上证明了通过LTD-BIC方法筛选伪分类后得到的模型具有相合性。 本节通过数值模拟的方式来验证第2节中提到的LTD-BIC方法在筛选伪分类的过程中具有相合性。模拟6个含有不同种类解释变量的Logistic模型,并通过LTD-BIC方法对模型中的伪分类进行筛选。所有的数值模拟用R语言实现。这6个包含OM变量的Logistic模型的真实系数向量设定如下: 模型1 β1=(0,2,2,4,4)T,α=(1,1)T; 模型2 β1=(0,2,2,4)T,β2=(0,3,5,5)T,α=(-4,-3)T; 模型3 β1=(0,3,3,3,3,3)T,α=(-4,1)T; 模型4 模型5 β1=(0,2,2,4,4,4,7.5,7.5,7.5,7.5)T,α=(1,1)T; 模型6 β1=(0,2,2,6,6)T,β2=(0,3,5,5,5,7,7,7,7)T,α=(-4.5,-3.5)T。 上述模型中,βi表示其对应模型中第i个OM解释变量X*i的系数向量;设定OM解释变量的第一个类别为基准类别,则βi中第一个分量的系数为0。α表示该模型的连续型解释变量。模型(1)~(6)中二元响应变量Y可由下式生成: 其中,Be(1,p)为伯努利分布。根据第二节的设定,如果β1中有相邻两个分量是相等的,则说明这两个分量对应的类别之间存在伪分类。例如,模型(1)中β1的第2,3个分量的值都为2,说明该模型的X*1中第2,3类之间存在伪分类,即Δβ1,3=β1,3-β1,2=0。需要探测出这些伪分类,并把2,3类合并为一类。同理,β1的第4,5个分量的值为4,则X*1中第4,5类之间也存在伪分类,所以应该把第4,5类合并为一类,那么在真实模型中X*1应正确类别为3类即可。其他模型中的伪分类可做类似说明。 为了进一步考察LTD-BIC的实用性,在模型(2)中设定包含两个OM变量,并设定两个连续型解释变量X*1和X*2,其系数向量分别为β1和β2;为了考察OM解释变量中的类别数量对筛选结果是否有影响,将模型(3)中的OM解释变量设定6个类别;为了考察LTD-BIC方法既能筛选OM变量中的伪分类又能筛选出对响应变量影响不显著连续型解释变量,在模型(4)中,设置1个OM解释变量的同时,设置5个与响应变量Y无关的连续型解释变量;为了考察OM解释变量中包含多个伪分类时对筛选结果是否有影响,在模型(5)的OM解释变量中设置10个类别;在模型(6)中,设置两个OM解释变量,并同时增加每个OM解释变量中的类别数,来考察LTD-BIC方法筛选伪分类的效果。 表1记录了模拟结果。从中可以看出,通过LTD-BIC方法筛选模型(1)~(6)中OM解释变量的伪分类时,模型覆盖率和选择正确率随着样本量N的增长是趋于1的。在模型(1)中,当样本量N从200增加到1 200的时候,模型覆盖率从0.71增加到1,而模型选择正确率也随之从0.69增加到0.98。从模型(2)的模拟结果中可以看到,在样本量较小时,模型覆盖率和模型选择正确率分别只有0.15和0.13,但是随着样本量增加,模型覆盖率和模型选择正确率也随之增加,这说明如果模型中存在两个以上的OM解释变量时,通过LTD-BIC方法筛选OM解释变量的伪分类同样具有模型相合性。通过模型(3)的模拟结果可以发现,当OM解释变量中只存在两个真实类别时,模型覆盖率和模型选择正确率在样本量很小的时候就已经接近1,这说明当OM变量中只有两个真实类别时LTD-BIC方法的筛选效果最佳。模型(4)的模拟结果显示,当样本量N从200增加到1 200时,模型覆盖率和模型选择正确率也分别从0.66和0.55增加到1.00和0.96,这说明LTD-BIC方法在筛选OM解释变量中伪分类的同时还能筛选出对响应变量Y的影响不显著的连续性解释变量。通过对比模型(1)和模型(5)的模拟结果发现,当OM解释变量中类别的数目增加时,每个子类别样本量相对减少,这使得模型覆盖率和模型选择正确率收敛到1的收敛速度会变慢,但是当样本量趋于无穷时,模型覆盖率和模型选择正确率会依然收敛到1。对比模型(2)和模型(6)可以发现,当OM解释变量中的类别数增多时,通过LTD-BIC方法选择的模型收敛到真实模型的收敛速度会越来越慢。综上,利用LTD-BIC方法筛选伪分类的方法具有相合性。然而,当OM解释变量中的类别个数增多时,通过LTD-BIC方法选择的模型收敛到真实模型的速度会降低。 表1 模型(1)~(5)基于1 000次模拟的模型选择结果 数据来自于成都市某中学不同年级学生的若干项目指标,纵向来看,该组数据是包含了横跨初中、高中六个年级总样本量N=2 446位同学的大样本数据;横向来说,该组数据主要统计了两类指标:一类是身体素质,包括性别、身高、体重;另一类是体测成绩,此类指标包括肺活量、五十米跑、立定跳远、坐位体前屈、800米跑(1 000米跑)、一分钟仰卧起坐(引体向上),以及通过某种线性运算得出的最终体测总成绩。通过运用本文提出的LTD-BIC方法,针对包含OM解释变量的Logistic回归模型中的伪分类进行筛选,从而展现该方法在处理实际问题时的可行性。为了便于分析,只选取以上给出的所有解释变量中的四个解释变量。 表2是对各个OM解释变量更加直观的描述。令OM解释变量中各个类别(除第一类)的子样本量的最小值和最大值之比表示为κ(·)。通过计算κ(·),来验证条件A2是否成立。这里由于X1为二分类解释变量,所以不做条件A2的验证。对于X2和X3,计算结果分别为κ(X2)=0.57,κ(X3)=0.75,且都大于0.5,这就说明了该数据可以满足条件A2。 表2 OM解释变量 以肺活量X2为例,首先通过卡方检验来确定肺活量的第2、3、4类对50米跑的成绩影响是否有显著性差别。卡方检验的具体步骤为: (1)确立原假设H0:肺活量的第2、3、4类对50米跑的成绩影响没有显著性差别; (3)其中,n表示当响应变量Y=1时X2的各个分类的样本量之和,fi和npi分别为X2中第i个分类在响应变量Y=1时的实际频数和理论频数,具体数值如表3所示; 由上述假设检验结果,得出了接受原假设的结论。也就是说,肺活量的第2、3、4类对50米跑的成绩影响没有显著性差别。由此事先可以推测这三个类别中可能存在伪分类。但是最终的定论还不能仅从单因素卡方检验中得到,接下来通过LTD-BIC方法来进行模型中的伪分类的筛选过程。 根据LTD-BIC算法,对表2中OM解释变量的哑变量进行线性变换后得到的全模型如下: 表3 卡方检验频数表 模型Ⅰ 接下来,运用LTD-BIC算法对OM解释变量中的伪分类进行筛选,得到筛选后的模型Ⅱ的表达式如下: 模型Ⅱ 对模型Ⅱ重新拟合,拟合结果如表5所示。 表4 模型Ⅰ参数估计结果 表5 运用LTD-BIC方法进行伪分类筛选后重新拟合的结果 接下来,将通过方差分析来检验模型Ⅰ和模型Ⅱ是否有显著性差异。其原假设为H0:模型Ⅰ和模型Ⅱ不存在显著性差异。通过调用R软件中Anova函数得到方差分析的结果,如表6所示。可以看出,由于P值大于0.05,应接受原假设,认为两模型不存在显著性差异。 表6 方差分析结果 表7 偏差分析结果 为了进一步比较上面两种模型,用交叉验证法(Cross-Validation)来比较究竟哪一种模型具有更好的预测能力。交叉验证是一种著名的数据挖掘方法,用于评估所选模型和参数在多大程度上可以推广到独立的样本外数据集的技术。k折交叉验证工作原理为,样本被分为k个子样本,轮流将k-1个子样本组合作为训练集,另外1个子样本作为预测集。从而得到k个预测模型,记录k个预测表现结果,然后求其平均值从而得到CV值。本例中运用5折交叉验证进行比较,将2 446组数据随机均分为5份,取其4份作为建立模型的训练集,然后对剩余的1份数据作为验证集做预测。在验证集里计算了模型验证正确率,CV值的公式表示为: 分别对模型Ⅰ和模型Ⅱ进行100次交叉验证,并取100次CV值的平均值作为最终结果,如表8所示。 从表8中可以看到,用LTD-BIC方法筛选出的模型Ⅱ的预测结果稍好一些。 表8 5折交叉验证结果 综上所述,得到的预测模型表示为: (24) 本文针对包含OM解释变量的Logistic回归模型,研究了一种新型的OM解释变量中伪分类筛选方法,并证明了该方法具有相合性的统计性质。通过仿真模拟的方式对LTD-BIC方法的相合性进行进一步论证。最后通过运用成都市某中学不同年级学生的若干项目指标数据这一实例来展现LTD-BIC方法的可应用性。在一般情况下,BIC选择准则稳定性较差,在包含多个OM解释变量时,随着样本量的增大筛选伪分类的模型覆盖率和模型选择正确率收敛到1的速度较慢,而且当一个OM解释变量中的类别数目过多时,也同样会出现用LTD-BIC方法选择的模型收敛到真实模型的收敛速度过慢的情况。对于高维甚至超高维的数据来说,BIC惩罚不再适用。因此,为了解决上述问题,在今后对于包含OM解释变量的广义线性模型的研究中,可以采用哑变量的线性变换结合LASSO类的惩罚似然方法来进行伪分类的筛选[19]。对于包含多个类别解释变量的回归模型,如果要同时进行组间关于响应变量无关的顺序类别解释变量筛选和组内伪分类筛选,可以考虑Group LASSO[20]+TD+penalty的方法进行筛选。对于回归模型中OM解释变量的维数随着样本量呈指数型增长时(log(pn)=O(nα),α>0),可以考虑通过Fan等提出的(I)SIS方法结合Group LASSO+TD+penalty方法进行高维特征筛选[21]。
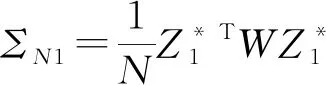

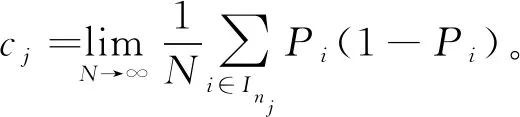


三、数值模拟


四、实证分析



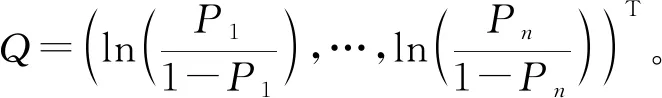
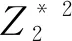




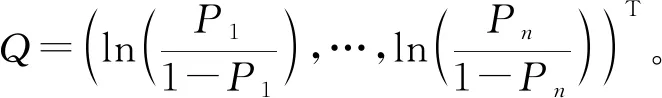
五、总结与展望
