空间滞后门限回归模型的估计

禚铸瑶

(1.中山大学 岭南学院,广东 广州 510275;2.华润金控投资有限公司,广东 深圳 518000)

一、引言

当数据结构出现截断效应,如极限环现象、跳跃共振现象和厄利效应等出现时,用普通线性回归模型常常无法有效拟合实际数据。为此,人们发展了门限回归模型(Threshold Regression Model),也称为样本截断回归模型(Sample Splitting Regression Model)。从20世纪80年代初至今,门限模型的模型形式和相关理论研究在不断地发展和完善。Tong首次详尽地介绍了时间序列数据的门限自回归(TAR)模型,Chan在Tong模型基础上证明了TAR模型的最小二乘估计量在一定假设条件下是一致估计量,并推导出门限变量的渐近分布服从一个复合泊松过程[1-2]。然而,由于门限变量的渐近分布存在一系列待估冗余参数,其置信区间的构造十分复杂。Hansen参照变点(changepoint)模型的相关理论,重新设计门限回归模型形式,解决了Chan中存在的冗余参数问题[3]。基于Hansen的门限回归模型,Caner和Hansen与Kourtellos,Stengos和Tan考虑内生性问题:前者假设模型中存在内生解释变量和外生门限变量,采用两阶段最小二乘估计法和矩估计法分别估计了门槛系数与普通回归参数,并获得了估计量的相合性和渐近正态性;后者认为内生门限变量的存在将导致参数估计存在偏误,进而提出集中两阶段最小二乘法纠正了这一问题[4-5]。除放松模型假设条件以外,另有一些研究在模型结构上做出了创新。例如,Cai和Stander与Cai在Koenker和Xiao的分位数回归的基础上,提出了依赖于门限变量分位数条件的分位数门限自回归模型,并给出待估参数的贝叶斯估计方法[6-8]。

Anselin认为计量模型如若忽略空间相关性的存在可能会产生模型设定错误、参数估计误差等一系列问题[9]。由于传统计量经济学方法往往难以描述经济现象中各空间单元(地区或者国家)间经济活动的溢出效应或相互依存关系,自20世纪70年代以来,空间计量经济学的理论和方法得到了迅速发展且应用广泛。Anselin总结了空间计量模型的构建、估计和检验等相关研究成果[9]。根据空间相依性表现形式的不同,空间计量模型可归纳为三类:空间滞后模型(也称为空间自回归模型)、空间误差滞后模型(也称为空间误差自回归模型)和混合空间模型(前两者的结合形式)。空间滞后模型(SLM)由Cliff和Ord首次提出,其最大特点是将某一空间单元的响应变量看作其他所有空间单元响应变量(空间滞后变量)的加权,能够直观地呈现出各空间单元间的相互依存关系[10]。Deng考虑数据可能存在的空间结构,提出具有门限空间效应的空间滞后模型,采用空间两阶段最小二乘法(S2SLS)估计待估参数,并证明了估计量的相合性质[11]。Deng的主要贡献在于对空间项的门限效应特征加以估计和证明。然而,当空间数据的门限效应不由个体相关度贡献而是存在于外生解释变量中时,我们尚没有发现相关的研究成果。

本文的主要贡献体现在三个方面。第一,本文将空间滞后项引入门限回归框架,构建一个新的空间滞后门限回归(Spatial Lag Threshold Regression,SLTR)模型,该模型的优点是能够同时捕捉数据的空间相关信息和数据截断特征。第二,本文给出了SLTR模型的截面极大似然估计方法,并推导出未知参数的相合性质和渐近正态性。第三,本文通过对比不同空间邻接矩阵(Rook矩阵、Queen矩阵和Case矩阵),不同空间相关性水平和门槛系数水平的Monte Carlo模拟计算得到估计量的有限样本性质,并对参数的估计稳健性展开了探讨,这将为实证研究中对空间邻接矩阵和样本量的选取提供参考。

二、模型设定和参数估计

(一)模型设定

考虑单门限空间滞后回归模型,其数学表达式为:

(1)

其中,Y=(y1,y2,…,yn)′为被解释变量n次观察值构成的向量,xi为k维解释向量的第i次观察值,门限变量qi为一维非随机观测变量,I{·}是示性函数。ρ为空间相关系数,Wn=(Wij)n×n为预先设定的空间邻接矩阵,(WnY)i代表(WnY)的第i个分量,样本依据门限变量与门槛值γ的大小关系分为两个机制(regime),k维回归系数向量β1和β2是两种机制区分的标志。随机误差项εi独立同分布地服从于正态分布N(0,σ2)。

为便于求解和推导,上式可等价地表达为:

(2)

其中,xi(γ)=xiI{qi≤γ},θ=β2,δ=β1-β2。

等价地,式(2)的矩阵表达形式为:

Y=ρWnY+Xθ+Xγδ+ε

(3)

其中,X=(x1,x2,…,xn)′和Xγ=(x1(γ),x2(γ),…,xn(γ))′是n×k的矩阵。

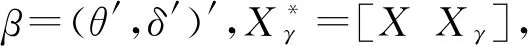
(4)

(二)参数估计步骤

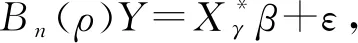
样本的对数似然函数表示为:

(5)

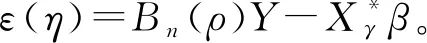
由于普通求极值的方法难以同时求得公式(5)中所有未知参数的有效最优解,因此本文使用截面极大似然估计方法(Profile Maximum Likelihood Method)分步求得未知参数的估计值。截面极大似然估计方法基于截面似然的思想,在每个阶段将冗余参数(nuisance parameter)用一致估计量替代,进而得到各参数的集中似然函数,求得未知参数的最优解[9,12-13]。具体实施步骤如下:

步骤1假定γ和ρ已知,利用集中极大似然法得到β(ρ,γ)和σ2(ρ,γ)的估计表达式:

(6)

(7)

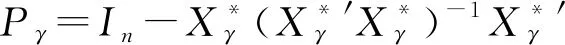
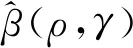
(8)

步骤2假定ρ已知,极大化集中对数似然函数(8),得到未知参数γ的估计量为:

(9)

由此可知,极大化对数似然函数即是极小化方差的估计值。

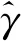
(10)

(三)估计的大样本性质

1.假设条件

首先,本文提出关于模型中变量的假定:

A1n×k维矩阵X中的元素一致有界;

A2 {εi}i=1,2,…,n独立同分布地服从于正态分布N(0,δ2),并且,{εi}i=1,2,…,n与{xi,qi}i=1,2,…,n相互独立。

其次,本文提出关于模型中常量的假定:

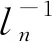
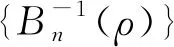
A1给出了非随机解释变量有界性,提供了证明所需要的矩条件;A2假设随机干扰项独立同分布,且与解释变量和门限变量不相关,保证了模型的同方差性和非内生性。Lee和Yu认为,当随机误差项存在异方差时,拟极大似然估计方法将无法得到一致估计量[14]。Kelejian和Prucha给出了异方差情形下的GMM估计方法[15]。A3与A4给出空间邻接矩阵的基本性质。

本文提出关于门限值γ、回归系数β的假定,并给出参数唯一可识别条件:

A6δ0=cγn-α,cγ是一个非零常数,0<α<0.5;k维回归系数向量θ0和δ0的元素有界,其中,θ0=β20,δ0=β10-β20,β10是β1的真值,β20是β2的真值;

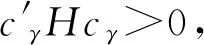
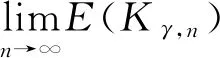
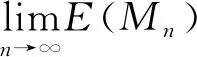
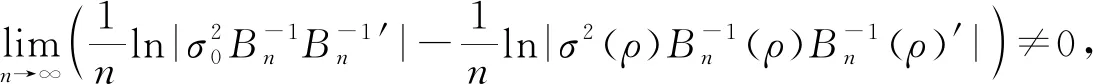
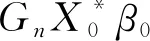
2.主要结论

在给出大样本性质前,先列出几个重要引理。

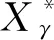
引理2满足假设条件A1～A7时,矩阵Pγ和(In-Pγ)一致有界。

引理3令φ=(β′,ρ,σ2)′,‖φ-φ0‖代表φ-φ0的Euclidean范式,Φ为φ0的一个邻域。在假设条件A1～A7和A8(或A9)下,lnLn(φ,γ)的海塞矩阵满足以下性质:

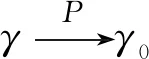
下面几个定理给出关心参数估计量的相合性和渐近分布。

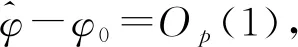
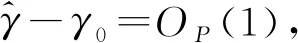
定理3在假设条件A1～A7和A8(或A9)下,有:

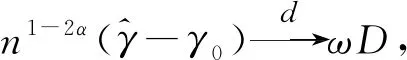
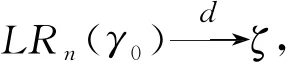
三、Monte Carlo模拟结果

本文采用Monte Carlo模拟方法评估估计量的小样本估计效果。常用的估计评价标准有偏差(Bias)、均方误差(Root Mean Square Error,RMSE)、标准差(Standard Deviation,STD)和分位区间(Interquantile Range,IQR)。前两者度量估计值与实际值的偏离程度,后两者从偏离均值程度和分位点表现两个的角度度量估计值本身的波动幅度。Bias、RMSE、STD和IQR定义如下:

(11)

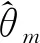
(一)数据生成过程

本文考虑如下数据生成过程:

第一,协变量矩阵X的元素{xij}i=1,2,…,n,j=1,2产生于均匀分布U(-3,3),门限变量qi产生于U(-1,1)的均匀分布。β1=(-0.5,1)′,β2=(0.5,2)′,空间自相关系数ρ和门槛系数γ均在[-0.8,0.8]内以步长0.1均匀取值。

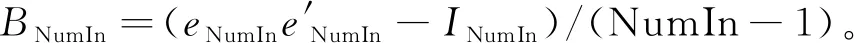
第三,随机干扰项ε的生成于标准正态分布ε～N(0,1)。

第四,Monte Carlo模拟次数M为499次。

将以上步骤生成的样本值和参数实际值带入式(1)计算,得到Monte Carlo模拟样本。

(二)数据模拟结果

本文利用499组模拟样本数据和式(6)至(10)估计待估参数,考察各参数估计量的偏差(Bias)、均方误差(RMSE)、标准差(STD)和分位数区间(IQR)的小样本表现。

1.普通数据模拟结果

以ρ=0.5,γ=0.3为例,参数模拟结果见表1和表2。观察表1,容易得到,在空间邻接矩阵为Rook矩阵和Queen矩阵时,参数向量β1、β2与参数ρ、γ和σ2的估计值与真实值相近,说明各个估计量的小样本表现良好,证明本文所提出的估计方法实用性强。

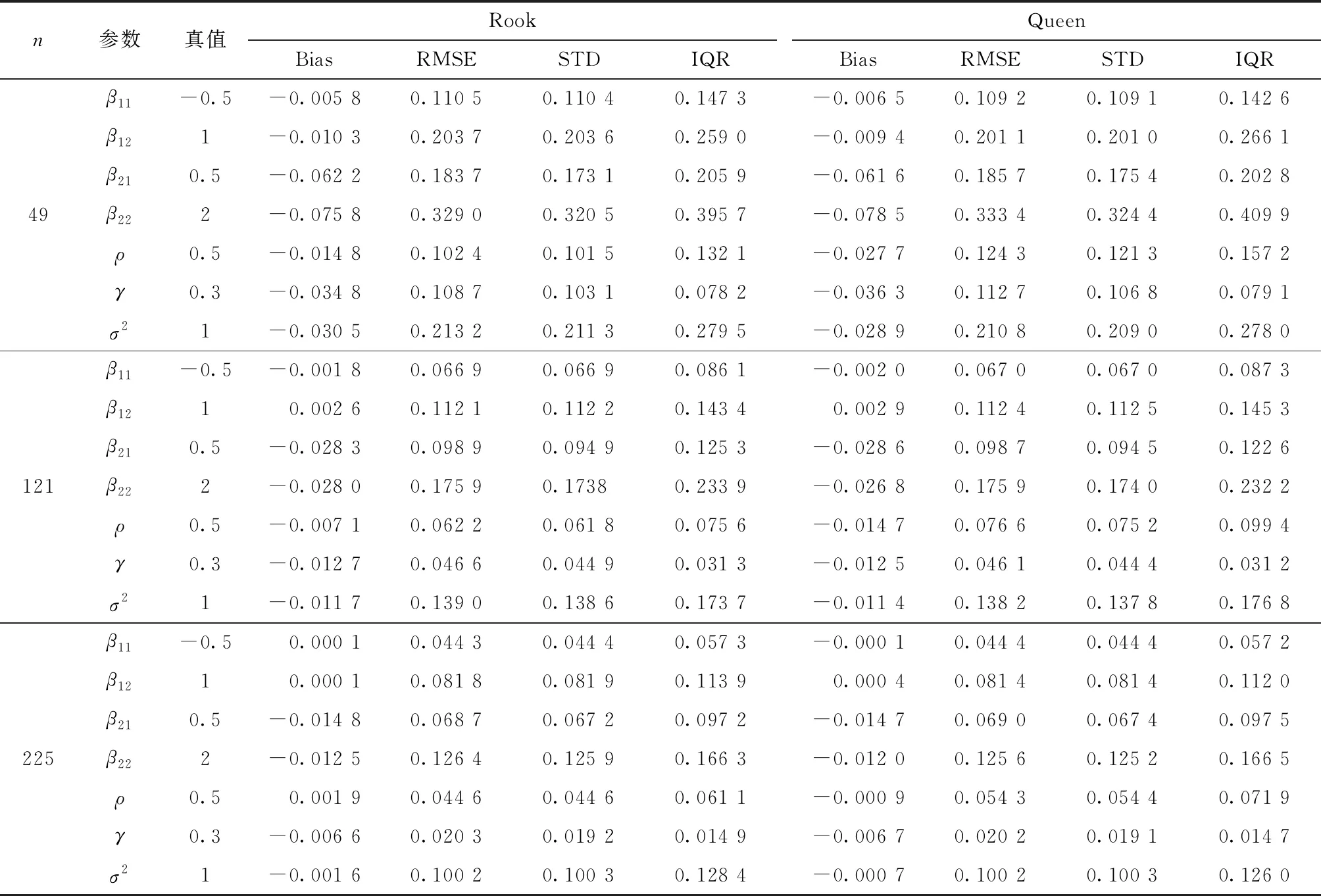
表1 参数模拟结果(Rook和Queen空间邻接矩阵)

具体地,在两种空间邻接矩阵设计下参数的估计偏误(Bias,RMSE)、标准差(STD)和分位区间(IQR)均随着样本个数n的增加而减小,说明随着样本容量的增大,参数估计偏误减小,且估计值呈现收敛特征。

观察表2,在空间邻接矩阵为Case矩阵时,参数向量β1、β2和参数ρ、γ和σ2的估计值与真实值均相近,说明各个估计量有较好的小样本表现。仔细观察数据特征,本文得出以下结论:第一,当空间复杂程度(区域内临界样本数NumIn)相同时,参数的估计值与实际值的估计偏误(Bias,RMSE)、标准差(STD)和分位区间(IQR)均随地区数(NumR)的增加而减小,说明地区数的增加使估计量收敛至真值。第二,当地区数相同时,空间相关系数ρ的估计偏误未随着空间复杂程度NumIn的增加而减小,而其余参数的估计评价指标均随着复杂程度增加呈明显的递减趋势。对比表1中Rook矩阵和Queen矩阵设计下ρ的估计表现,我们认为,对于空间滞后门限模型,空间复杂度的增加抵消了样本容量增加带来的ρ的估计偏误的减少。综合上述结果,我们认为在Case矩阵设计下,空间复杂度相同时参数估计值具有依样本量增大而收敛至真实值特征;在地区数相同时,ρ的估计偏误尽管较小但不会因为样本量增大而收敛,而其他参数表现出明显的收敛于真实值的特征。

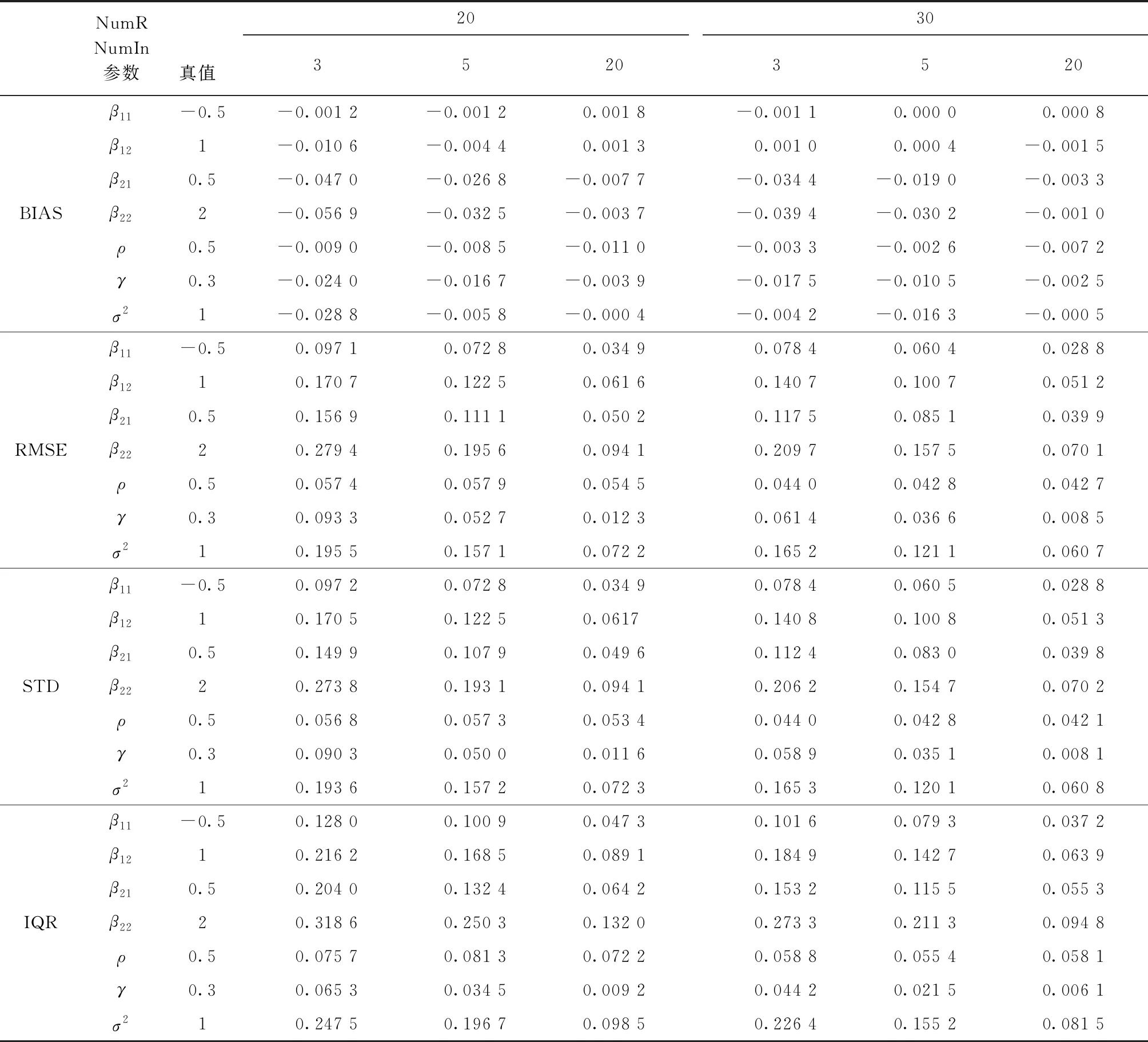
表2 参数模拟结果(Case空间邻接矩阵)

总而言之,无论在何种空间邻接矩阵设计下,各参数估计量具有依样本量增大而收敛至真实值的特性。由于空间滞后门限模型融合了空间滞后效应和门限效应,相较空间滞后回归模型增加了门限特征,相比门限回归模型增添了空间滞后效应。为了全面展现新模型估计结果,我们将分别讨论空间自相关系数ρ和门槛系数γ变化时参数估计量的评价指标表现,并探讨其稳健性。

2.变空间自相关系数的模拟结果分析

空间相关性的强弱代表着相邻接的空间单元间相互影响程度的大小。如果空间相关程度的大小不影响其他参数(如斜率向量β1和β2和门槛系数γ等)的估计效果,说明估计方法稳定;反之,说明空间相关系数的大小影响其他参数的估计效率,估计方法不稳定。为此,本文模拟并计算了空间自相关系数ρ在[-0.8,0.8]内以步长0.1均匀取值时所有参数的估计结果。

为了对比不同空间邻接矩阵设定下参数估计量的表现规律,本文将考虑两类空间邻接矩阵:Rook和Queen矩阵;Case矩阵。前者通过定义空间单元的公共边界和公共节点定义邻接矩阵(Anselin);后者考虑区域内部邻接关系,被广泛应用于社会交互模型中(Case)[9,16]。

(1)Rook和Queen空间邻接矩阵

图1给出了两种空间邻接矩阵设计下,样本量不同时各参数估计量的偏差(Bias)情况。观察图形,可得到以下两点结论。一方面,偏差水平随样本增加而缩减。无论空间相关程度和样本量如何,各参数估计量的Bias在参数真实值的10%以内;样本量最小时(N=49)各参数估计量的Bias最大;随着样本量的增加,Bias越来越靠近0,说明无论空间相关程度如何,样本量的增加使参数估计值偏误缩小。另一方面,偏差对空间相关系数的敏感度随样本增加而减弱。当样本量较小时,Rook矩阵设计下的β11、β12、β22和σ2的估计偏误受到空间相关程度ρ变动的影响,ρ的绝对值越大越陡峭;Queen矩阵设计下的结果类似,在ρ>0时更加明显;在样本量较大时,各参数偏差波动较小,图形平缓,因此可以说明偏差随空间相关系数变动的敏感程度减弱了。

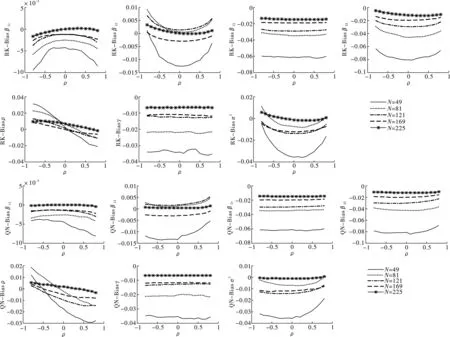
注:图中纵轴名称中RK代表Rook权重矩阵计算结果,QN代表Queen权重矩阵计算结果,后文相同。

观察图2至图4,本文发现在两种空间邻接矩阵设计下,各参数估计量的均方误差(RMSE)、标准差(STD)和分位数区间(IQR)呈现以下特征。第一,所有参数估计量的指标值随样本增加而递减。样本量最小时各参数估计量的指标值最大;随着样本量的增加,各指标值越来越接近0,说明无论空间相关程度如何,样本量的增加使参数估计值误差和波动幅度缩小。第二,参数估计量(不含ρ)的指标值与ρ的大小无关,结果稳健。无论样本量大小或邻接矩阵如何,除ρ以外的参数估计值与ρ的曲线为一条近乎水平的直线,这意味着空间相关程度的大小不影响估计量的收敛性。第三,间相关性增强而递减,ρ<0时其表现因邻接矩阵不同存在差异。具体地,在ρ<0时,ρ越靠近-1,估计量(Rook矩阵)的指标值越小;估计量(Queen矩阵)的指标值越大。

ρ>0时空间相关系数估计量的各指标值随实际空

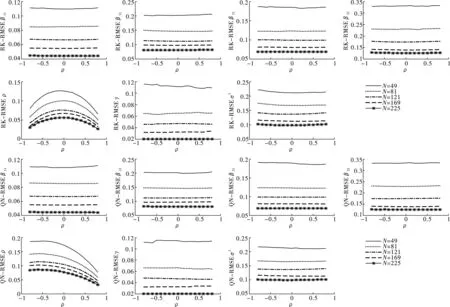
图2 参数估计RMSE对比图(Rook和Queen空间邻接矩阵)

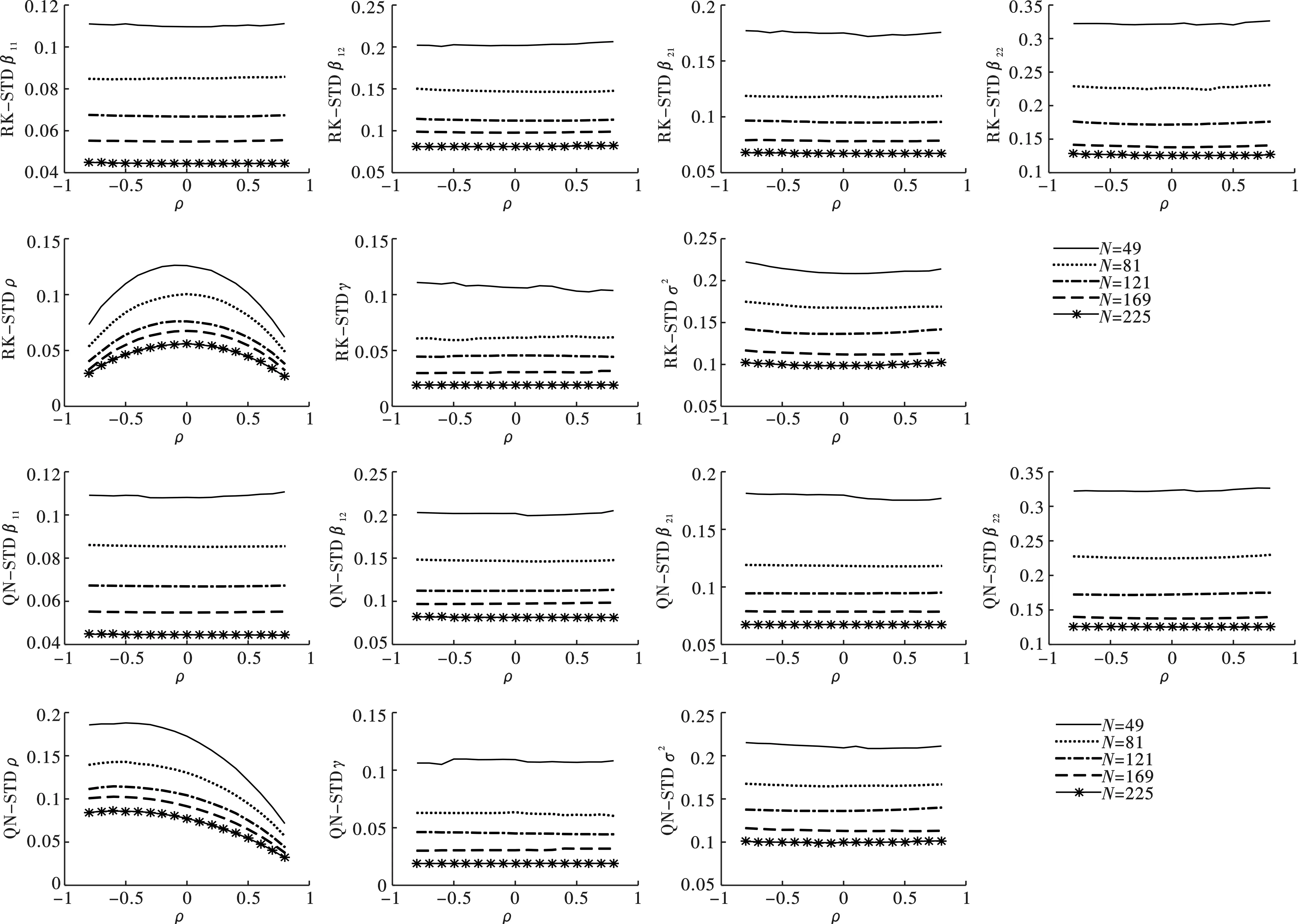
图3 参数估计STD对比图(Rook和Queen空间邻接矩阵)

图4 参数估计IQR对比图(Rook和Queen空间邻接矩阵)

综合图1至图4的分析,本文发现在Rook和Queen空间邻接矩阵设计下,无论空间相关系数如何变化,参数估计量的估计偏误和波动幅度均随样本增加而减小;当N>81时,参数估计量(不含ρ)的估计偏误和波动幅度并未受到ρ大小的影响;ρ>0时空间相关系数估计量的估计偏误和波动幅度随实际空间相关性增强而减小,在ρ<0时,ρ越靠近-1,估计量(Rook矩阵)的估计偏误和波动幅度越小,估计量(Queen矩阵)的估计偏误和波动幅度越大,说明当空间单元相互产生负向影响时,Rook矩阵设计下的空间相关系数估计量比Queen矩阵情形更稳定。总而言之,本文提出的参数估计量具有两个重要的优良性质。其一,相合性:参数估计量依样本量增大而收敛于真实值,印证了定理1～4中各参数估计量满足相合性的结论;其二,稳健性:当样本量较大时,估计量对ρ的变化不敏感,估计量表现稳健。另外,关于空间相关系数的结论为空间邻接矩阵的选取提供了有益参考。

(2)Case空间邻接矩阵

图5给出了Case空间邻接矩阵设计下,样本量不同时各参数估计量的偏差(Bias)情况。观察图形,可得到以下几点结论。第一,参数估计量(不含ρ)的偏差(Bias)随样本数(NumR或NumIn)增加而递减。在区域内邻接单元个数(NumIn)相同时,各参数估计量的偏差(Bias)幅度较小(<10%)且随区域数NumR增加而减小;在区域数(NumR)相同时,各参数估计量的偏差(Bias)幅度较小(<10%)且随区域数NumR增加而减小。第二,参数估计量(不含ρ)的偏差敏感度随样本增加而减弱。β21与γ图形呈直线表明其不受空间相关程度大小的影响;β11、β12、β22和σ2受到空间相关程度ρ变动的影响程度较大,但随着样本数(NumR或NumIn)的增加其影响程度逐渐减弱。第三,ρ估计量的平均偏差随实际空间相关水平或区域数(NumR)增加而减小,但随着区域内邻接单元个数(NumIn)的增加而增强。Lee证明了区域内邻接单元个数(NumIn)过多,将导致信息矩阵渐近奇异,空间相关系数ρ的截面极大似然估计(PMLE)收敛速度降低,本文的结果与Lee的结论一致[17]。因此,我们认为在区域数(NumR)不变、区域内邻接单元个数(NumIn)增加时,ρ的估计量存在估计偏差,且空间结构越复杂或空间相关系数越小,估计偏差水平越大。

观察图6至图8,发现在Case空间邻接矩阵设计下,各参数估计量的均方误差(RMSE)、标准差(STD)和分位数区间(IQR)呈现出以下三个特征。

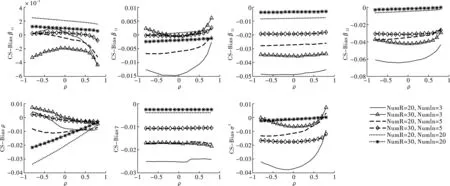
图5 参数估计Bias对比图(Case空间邻接矩阵)

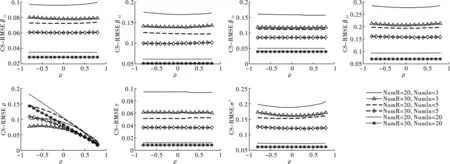
图6 参数估计RMSE对比图(Case空间邻接矩阵)

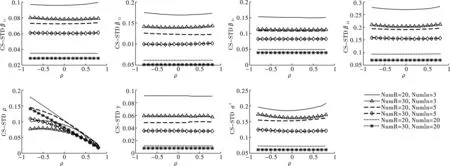
图7 参数估计STD对比图(Case空间邻接矩阵)

第一,参数估计量(不含ρ)的三个指标随样本数(NumR或NumIn)增加而递减。在区域内邻接单元个数(NumIn)相同时,各参数估计量的三个指标数值随区域数(NumR)增加而减小;在区域数(NumR)相同时,各参数估计量的三个指标数值随区域内邻接单元个数(NumIn)增加而减小。第二,参数估计量(不含ρ)的三个指标数值与ρ的大小无关,结果稳健。无论样本量(NumR或NumIn)如何,除ρ以外的参数估计值与ρ的曲线为一条近乎水平的直线,这意味着空间相关程度的大小不影响估计量的均方误差水平、标准差和分位数区间。第三,空间相关系数ρ估计量的三个指标数值随实际空间相关水平或区域数(NumR)增加而减小,但随区域内邻接单元个数(NumIn)的增加而增大。

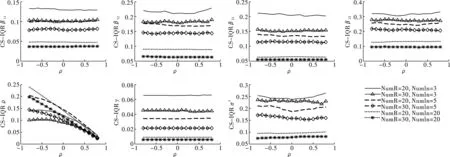
图8 参数估计IQR对比图(Case空间邻接矩阵)

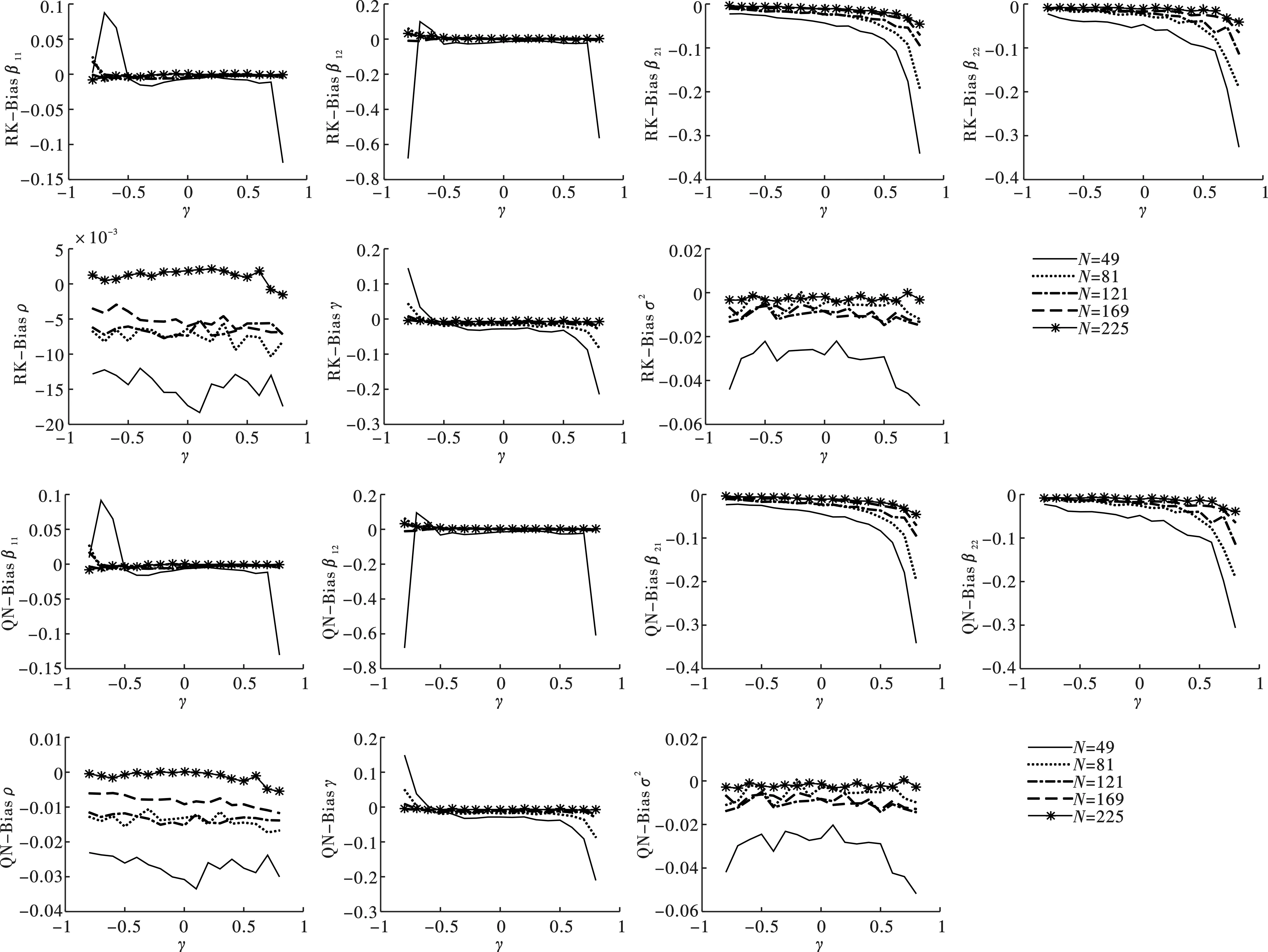
图9 参数估计Bias对比图(Rook和Queen空间邻接矩阵)

综合图5至图8的分析,发现在Case空间邻接矩阵设计下,无论空间相关系数如何变化,参数估计量(不含ρ)的估计偏误和波动幅度均随样本数(NumR或NumIn)增加而减小;空间相关系数ρ估计量的估计偏误和波动幅度随实际空间相关水平或区域数(NumR)增加而减小,但随区域内邻接单元个数(NumIn)的增加而增大。因此,在控制区域内邻接单元个数(NumIn)个数为一个小值时,本文提出的参数估计量具有两个重要的优良性质。其一,相合性:参数估计量依样本量增大而收敛于真实值,印证了定理1～4中各参数估计量满足相合性的结论;其二,稳健性:当样本量较大时,估计量对ρ的变化不敏感,估计量表现稳健。

3.变门槛系数的模拟结果分析

门槛系数γ的大小影响着解释变量作用于被解释变量的机制关系。如果门槛系数大小不影响其他参数(如斜率向量β1和β2和空间自相关系数ρ等)的估计效果,说明估计方法稳定;反之,说明门槛系数的大小影响其他参数的估计效率,估计方法不稳定。为此,本文模拟并计算了门槛系数γ在[-0.8,0.8]内以步长0.1均匀取值时所有参数的估计结果,如图9～16所示。

(1)Rook和Queen空间邻接矩阵

图9给出了两种空间邻接矩阵设计下,样本量不同时各参数估计量的偏差(Bias)情况。观察图形,可得到以下两点结论。一方面,偏差水平随样本增加而缩减。无论门槛系数γ大小如何,随着样本量的增加,Bias越来越靠近0,说明样本量的增加使参数估计值偏误缩小。

另一方面,偏差敏感度随样本增加而减弱。当样本量较小时,Rook和Queen矩阵设计下的β11、β12、γ和σ2估计量的估计偏误在真实的γ靠近数值边界时,偏差陡增;β21和β22估计量的估计偏误在真实的γ靠近右侧边界时,偏差陡增。随着样本量的增加,各参数估计量偏误水平区域逐渐收敛且平稳地分布在0附近。Hansen提出用搜索法获得γ的估计值,将门限变量样本域按数值顺序排序去除两端样本5%,防止样本过少产生估计偏误[3,18]。通过模拟实验,发现当样本量过少时(N=49),各参数估计量在γ的真实值靠近边界时出现估计偏差,而在样本量较大时(N→225)偏差不受影响。因此,本文既为Hansen去除两端样本的做法提供了依据,又为样本量的确定提供了有益参考。

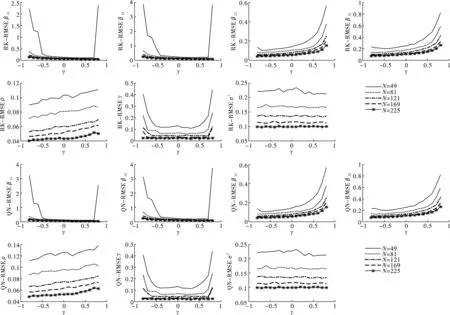
图10 参数估计RMSE对比图(Rook和Queen空间邻接矩阵)

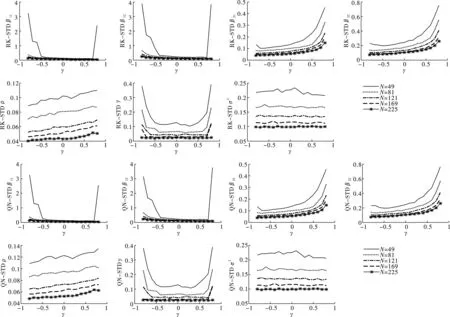
图11 参数估计STD对比图(Rook和Queen空间邻接矩阵)

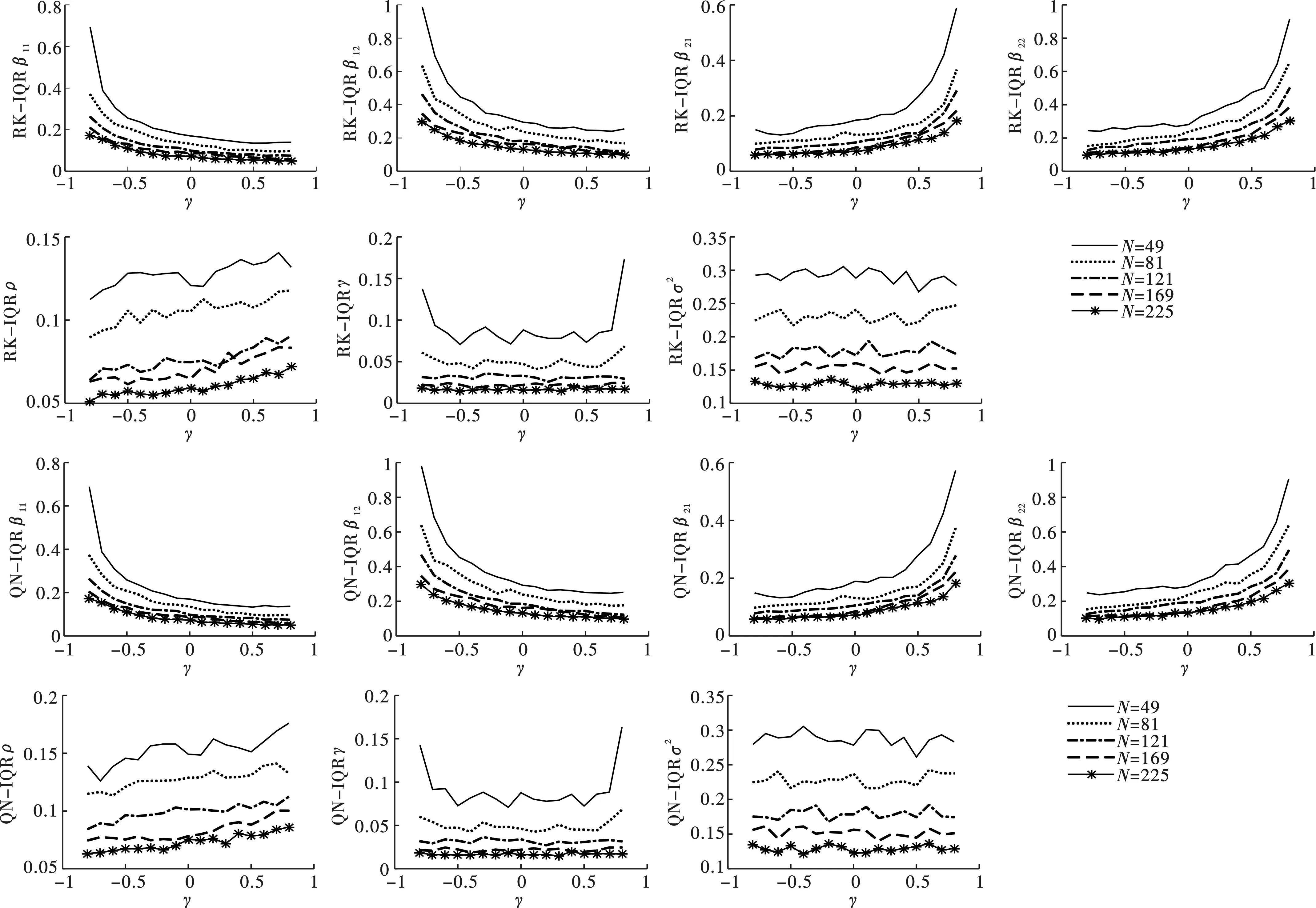
图12 参数估计IQR对比图(Rook和Queen空间邻接矩阵)

图10至图12展示了两种空间邻接矩阵设计下,样本量不同时各参数估计量的均方误差(RMSE)、标准差(STD)和分位数区间(IQR)的变化特征。可以发现,三种指标数值特征相似,基本可以概括为以下特点。第一,所有参数估计量的指标数值依样本量增加呈递减趋势,说明无论门槛系数γ大小如何,样本量的增加使参数估计值估计偏误和波动幅度缩小。第二,三种指标敏感度随样本增加而减弱。当样本量较小时,Rook和Queen矩阵设计下的β11、β12、γ和σ2估计量的指标数值在真实的γ靠近数值边界时,偏差陡增;β21和β22估计量的三种指标数值在真实的γ靠近右侧边界时,偏差陡增。随着样本量的增加,各参数估计量估计偏误和波动幅度稳健地逐渐收敛趋近于0。

综合图9至图12的分析,发现在Rook和Queen空间邻接矩阵设计下,无论门槛系数如何变化,参数估计量的估计偏误和波动幅度均随样本增加而减小,指标敏感度随样本增加而减弱,两种矩阵设计下参数估计结果相似。总而言之,我们发现参数估计量具有两个重要的优良性质。其一,相合性:参数估计量依样本量增大而收敛于真实值,印证了定理1～4中各参数估计量满足相合性的结论。其二,稳健性:当样本量较大时,估计量对γ的变化不敏感,估计量表现稳健。

(2)Case空间邻接矩阵

图13给出了Case空间邻接矩阵设计下,样本量不同时各参数估计量的偏差(Bias)情况。观察图形,可得到以下几点结论。第一,参数估计量(不含ρ)的偏差(Bias)随样本数(NumR或NumIn)增加而递减。在区域内邻接单元个数(NumIn)相同时,各参数估计量的偏差(Bias)随区域数NumR增加而减小;在区域数(NumR)相同时,各参数估计量的偏差(Bias)随区域数NumR增加而减小。第二,参数估计量(不含ρ)的偏差敏感度随样本增加而减弱。Rook和Queen矩阵设计下β11、β12和γ估计量在γ的真实值靠近左边界时,呈现陡峭的正偏差;β21、β22和γ估计量在γ的真实值靠近右边界时,呈现陡峭的负偏差。但以上估计量随着样本数(NumR或NumIn)的增加其偏差幅度逐渐减弱。第三,ρ估计量的偏差随区域数(NumR)增加而减小,但随着区域内邻接单元个数(NumIn)的增加而增强,与γ关系不大。因此,本空间滞后门限回归模型中空间自相关系数ρ的截面极大似然估计量的估计偏差在Case空间邻接矩阵情形下存在,结论与空间滞后回归模型相似,与门槛效应γ大小无关。

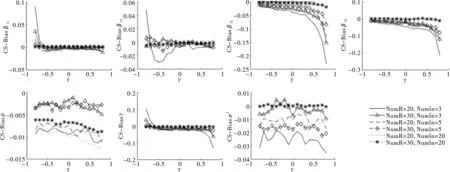
图13 参数估计Bias对比图(Case空间邻接矩阵)

观察图14至图16,发现在Case空间邻接矩阵设计下,各参数估计量的均方误差(RMSE)、标准差(STD)和分位数区间(IQR)呈现出以下三个特征。第一,参数估计量(不含ρ)的三个指标数值随样本数(NumR或NumIn)增加而递减。在区域内邻接单元个数(NumIn)相同时,各参数估计量的指标数值随区域数(NumR)增加而减小;在区域数(NumR)相同时,各参数估计量的指标数值随区域内邻接单元个数(NumIn)增加而减小。第二,三个指标(不含ρ)的偏差敏感度随样本增加而减弱。β11、β12和γ估计量在γ的真实值靠近左边界时,三个指标数值陡增;β21、β22和γ估计量在γ的真实值靠近右边界时,三个指标数值陡增。但随着样本数(NumR或NumIn)的增加其偏离幅度逐渐减弱。第三,空间相关系数ρ估计量的三个指标数值随区域数(NumR)增加而减小,但与区域内邻接单元个数(NumIn)和γ变动关系不大。

综合图13至图16的分析,发现在Case空间邻接矩阵设计下,无论门槛系数γ如何变化,参数估计量(不含ρ)的估计偏误和波动幅度均随样本数(NumR或NumIn)增加而减小;空间相关系数ρ估计量的估计偏误和波动幅度随实际空间相关水平或区域数(NumR)增加而减小,但与区域内邻接单元个数(NumIn)和门槛系数关系不大。本文提出的参数估计量具有两个重要的优良性质。其一,相合性:参数估计量依样本量增大而收敛于真实值,模拟结果印证了定理1～4中各参数估计量满足相合性的结论;其二,稳健性:当样本量较大时,估计量对γ的变化不敏感,估计量表现稳健。

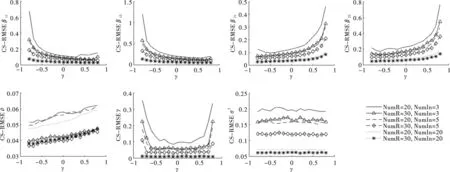
图14 参数估计RMSE对比图(Case空间邻接矩阵)

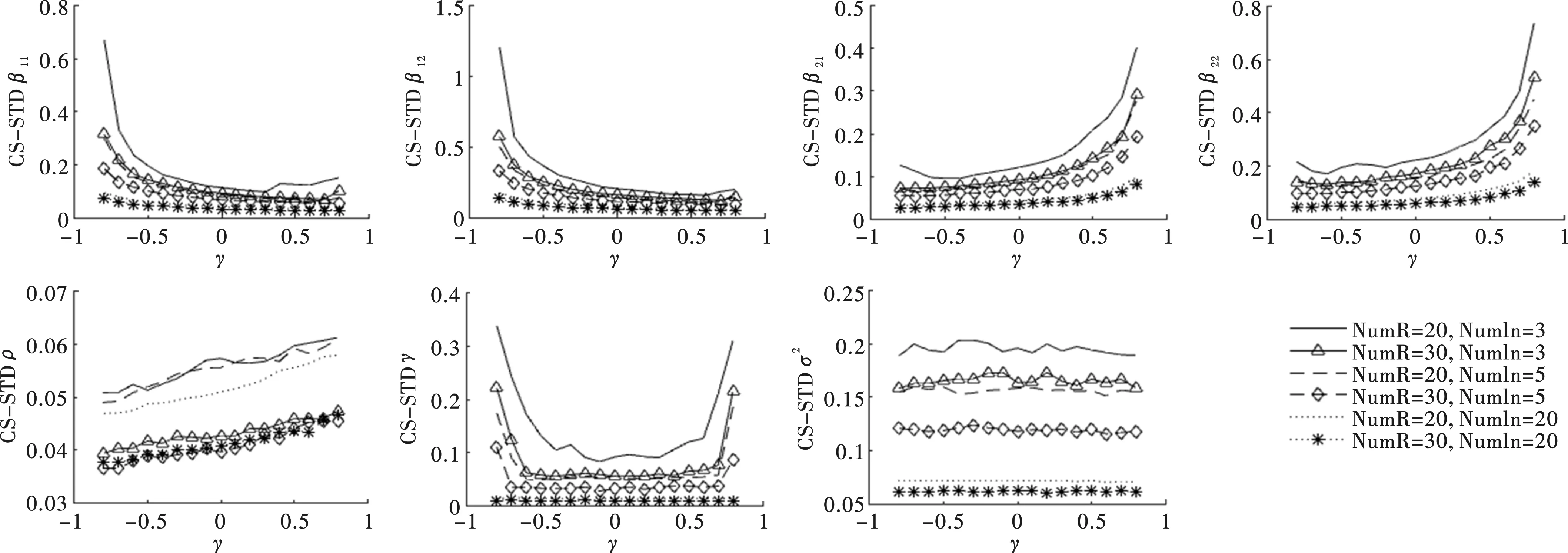
图15 参数估计STD对比图(Case空间邻接矩阵)

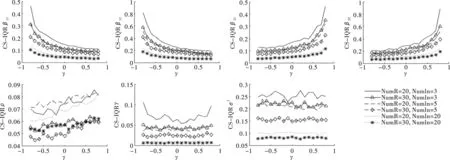
图16 参数估计IQR对比图(Case空间邻接矩阵)

四、结论

传统的门限回归模型在应用于截面空间数据时可能会因忽略空间相关性产生估计误差。无论是理论分析还是实证应用,对空间门限模型的研究仍处于起步阶段,目前尚未有考虑外生门限效应的空间计量模型的相关研究。本文基于截面数据框架,将空间滞后模型和门限回归模型融于一体,即同时考虑了空间外部性和解释变量可能存在的门限效应特征,以期拓宽空间模型和门限模型的应用领域。针对该模型,本文利用截面极大似然估计法,给出了理论证明和数值模拟结果。

经过理论推导,本文证明出基于截面数据的空间门限模型中,空间相关系数ρ和门槛系数γ等待估参数的截面极大似然估计量满足相合性。此外,回归参数估计量具有渐近正态性。在Monte Carlo数值模拟中,本文考虑了Rook空间临邻接矩阵、Queen空间邻接矩阵和Case空间邻接矩阵三种情形,并针对空间相关系数和门槛系数的数值变动可能对其他参数的估计量产生的影响进行了对比讨论。得到相关结论如下:(1)各估计量的估计偏误(Bias和RMSE)和波动幅度(STD和IQR)较小,且随着样本容量的增加而减小,表明各个估计量小样本表现良好且与理论结果一致;(2)估计量对空间相关系数ρ和门槛系数γ的变化的敏感程度随着样本量的增加而降低,说明估计量满足大样本稳健性;(3)当实际空间相关系数ρ为负值时,相较于Queen空间邻接矩阵,Rook矩阵设计下求得ρ的估计量偏误更低,波动幅度更小,这为空间权重矩阵的选取提供有益参考;(4)当空间邻矩阵为Case类型时,空间相关系数ρ的估计量对于空间复杂程度颇为敏感,其估计精度在一定程度上受复杂程度的影响,然而,样本容量的增加能够克服这种影响并改善其估计的稳健性;(5)在样本量较小时,各参数估计量在门槛系数γ的真实值靠近边界时出现估计偏差,而在样本量较大时较不受影响,这既印证了Hansen估计γ时去除极端数据的做法,又为样本量的确定提供了依据。

感谢陈建宝教授在本文写作过程中给予了诸多指导与建议。本文附录部分因版面所限省略。