基于AGA8-92DC模型的天然气压缩因子计算软件开发与应用
2021-03-17何冬辉
何冬辉
(辽宁东科电力有限公司,沈阳 110006)
0 引 言
天然气压缩因子,又称天然气偏差系数,指在环境温度、压力下,真实气体在相同条件下所占体积与相同量理想气体所占体积的比值[1-2]。该参数是天然气流量计算的最关键中间物性参数之一,其计算精度直接影响天然气流量的计算精度。近年来,随着燃气轮机的广泛应用,天然气常在非理想气体工况下(压力不大于1 MPa,温度范围不超过10~20 ℃)传输。在非理想气体工况下,天然气的流量计算需要在理想气体状态方程的基础上引入压缩因子。计算机高新技术的发展极大地提高了压缩因子计算的精度和效率,其中基于AGA8-92DC模型的计算方法得到了国际标准化组织天然气技术委员会的推荐。AGA8-92DC模型以状态方程为基础,因其计算精度较其他方法高而得到了广泛应用。该文以AGA8-92DC为计算模型,优化压缩因子迭代算法,采用面向对象编程的C#语言,设计并实现了天然气压缩因子计算软件开发。
1 AGA8-92DC计算模型
1.1 计算模型介绍
美国标准学会以孔板流量计标准AGA No.3报告为基础,对天然气压缩因子开展了深度研究,并发表了基于状态方程的压缩因子计算方法的AGA No.8报告,即AGA8-92DC方程。该方程的出发点是:任何天然气容量性质均可由一组合适的可测定物性值来表征和计算[1]。通过分析试验气体摩尔成分超过0.000 05的各种气体组分,输入实际工况下的压力和温度来计算压缩因子。该方程的实际应用条件为:输气管内气体绝对压力为0~12 MPa,温度范围为263~338 K,计算结果不确定度约为0.1%。AGA No.8号报告中,以气体组分成分为基础进行计算的方程如式(1)所示,以气体物理特性数据为基础进行计算的方程如式(2)所示,前者属于外延式二维维里方程,后者属于三维维里方程。
(1)
(2)

1.2 计算过程
1.2.1 已知条件
该计算模型通过分析取样气体详细的摩尔分数组成,并根据实际工况压力、温度来计算气体压缩因子。
已知参数包括气体实际工况下的气体摩尔组分数N、绝对压力p和热力学温度T。
气体摩尔组成以摩尔百分数表示各气体组分,气体包括CO2、N2、H2、CO、CH4、C2H6、C3H8、i-C4H10、n-C4H10、i-C5H10、n-C5H12、n-C6H14、n-C7H16、n-C8H18。
气体各组分的摩尔分数分别表示为Xi,i=1~N。

1.2.2 计算步骤
1)计算第二维里系数B。
(3)
(4)
(WiWj+1-wn)wn
二元参数Eij和Gij,由以下两式计算得出:
(5)
(6)
(7)
根据式(8)~(11)分别求解混合方程,计算混合物参数U,G,Q,F。
(8)
(9)
(10)
(11)
3)计算混合物体积参数K。
(12)
4)计算对比密度。
摩尔密度为:
ρm=p/(ZRT)
(13)
式中:T为热力学温度,K;R为摩尔气体常数;p为绝对压力,MPa。
对比密度ρr与摩尔密度ρm相关:
ρr=K3ρm
(14)
5)根据以上计算系数,代入式(1)所示的AGA8-92DC方程,用迭代方法求解天然气压缩因子。
1.3 算法优化
根据利用AGA8-92DC模型计算天然气压缩因子的过程可看出,运算需要多次运用连加、二重求和甚至三重求和等数学方法,依次计算58种物质的变量状态方程参数、21种识别组分的特征参数、21种识别组分的二元交互作用参数组[2],求解方程时需多次进行二次插值和迭代计算。计算过程不仅复杂,而且计算误差大、结果不准确。为解决上述问题,对迭代算法和流程进行全面优化,用弦截法代替牛顿迭代法。弦截法是以牛顿迭代法为基础,利用差商代替牛顿法中的导数值,通过迭代实现变种及优化的算法,不仅收敛速度快,还避免了复杂计算函数导数值问题。弦截法的核心思想是用切线斜率近似割线斜率[3],与牛顿迭代法相比,其计算量少且条理清晰,便于算法程序开发。
根据式(3)~(12),计算各种辅助参数后,通过迭代计算摩尔密度以得到压力p2,根据标准中定义将计算流程归纳如下:
1)初始化摩尔迭代计算初值,p1、p2;
2)计算摩尔密度ρn和低阶摩尔密度ρn-1;
3)当计算数值与初始值的误差过大时,迭代计算新的密度ρn+1;
4)重新计算最新密度,然后重复地第2)至4)步,直到计算所得压力p计算与实测压力p输入之差的绝对值小于10-6。
当计算所得压力与测量压力之间的误差小于一定范围后,即得到压缩因子的计算值,根据式(1)进行压缩因子计算,其计算流程如图1所示。采用AGA8-92DC标准计算天然气压缩因子,算法流程主要分为4个步骤:调用已经验证过的待计算数据并进行初始化操作、辅助参数计算、迭代计算、压缩因子和密度计算。压缩因子迭代计算流程中定义状态参数函数、特征参数函数、二元交互作用参数函数三组结构,分别对应计算标准中变量状态方程参数、特征参数、二元交互作用参数组。压缩因子计算初始化过程需校验相关计算参数数值的合法性,随后根据AGA8-92DC标准以键值数据形式格式化计算参数寄存器以备调用,其详细工作流程如图1所示。
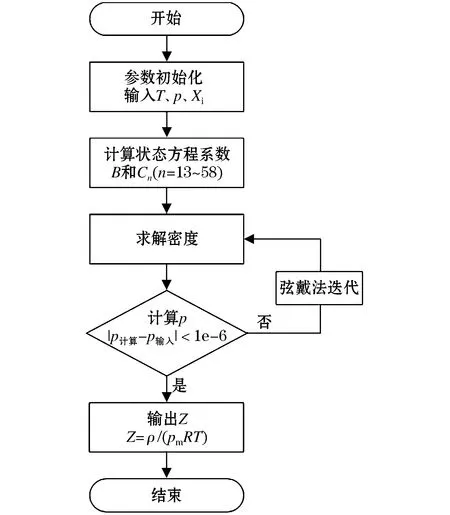
图1 迭代计算流程Fig.1 Flow chart of iterative calculation
压缩因子迭代计算占用了该算法的主要计算资源,因此消减压缩因子迭代计算可显著提高算法的计算效率。主要方式是优化压缩因子算法中迭代计算流程,通过快速迭代得出满足|p2-p1|<10-6条件的摩尔密度ρm,使压缩因子计算算法性能得以提高,其中,p1为实测压力,p2为计算压力,由式(15)计算得出。
p2=ρnTRZ
(15)
根据(15)可知,p2是1个关于ρn的函数,可表达为式(16):
p2=p(ρn)
(16)
设f(ρn)是一个关于ρn的函数,且满足式(17):
f(ρn)=P(ρn)-p1
(17)
根据式(17)可以看出,f(ρn)是1个关于ρn的单调函数,当P(ρ0)=p1时,f(ρ0)=0,那么P(ρn)=p1就是f(ρ0)的根,即式(17)可使用弦截法求解。当P(ρn)=0时,f(ρn)=-p1,-p1<0,那么f(ρn)是一个单调递增函数。结合式(15)~(17)可知求解|p2-p1|<10-6的过程即等同于求满足f(ρn)<10-6的pn值。
使用快速收敛的弦截法(见图2)求式(17)的详细步骤如下所述。

图2 弦截法示意图Fig.2 schematic diagram of secant method
1)根据GBT 17747.2—2011标准可知,0≤ρn≤8,根据ρn范围,设P(ρ0)=p1即f(ρ0)=0,选取ρ1=0,ρ2=15为迭代初始值,控制精度为10-6。根据式(17)计算f(p1)=f(ρn-1)、f(ρ2)=f(ρn)的值,此时n=2,n-1=1,n+1=3。
2)根据式(17)、(18),分别求解ρn+1及f(ρn+1)的值。
(18)
3)对f(ρn-1)、f(ρn)、f(ρn+1)的值进行判断。由于f(ρn)是一个单调递增函数,那么f(ρn-1) ①若f(ρn+1)<0且|f(ρn-1)|>|f(ρn+1)|>10-6,则赋值令n=n、n-1=n+1,重复2)与3); ②若f(ρn+1)>0且|f(ρn)|>|f(ρn+1)|>10-6,则令n=n+1、n-1=n-1,重复2)与3); ③若|f(ρn+1)|<10-6,则停止计算,此时的ρn+1即需要计算的ρm,迭代计算结束。 基于软件功能需求,采用面向对象程序的C#语言在Visual Studio.NET的WPF框架下对天然气压缩因子计算软件进行设计,实现人机交互可视化界面、输入输出数据处理、核心计算动态链接库(Dynamic Link Library,DLL)等模块的构建。天然气压缩因子的计算主要针对实际工况下天然气的详细组分进行计算,因此该程序共分为2个部分:人机交互界面部分和核心计算DLL部分。系统界面部分主要负责参数输入和校验、核心计算模块的调用和计算结果的输出显示。核心计算DLL部分负责对输入参数进行计算。系统的计算功能在用户界面窗口实现,用户通过界面窗口与系统交互,界面组件接受数据输入并检测用户输入合法性,输入非法数据将提示用户。待数据输入完整且正确后,点击“计算”按钮,系统调用核心计算DLL计算模块,将最终计算结果绑定到界面组件并输出显示。 考虑到压力和温度有多种计量单位,为体现交互界面的直观友好,系统提供多种单位数据输入模式,用户可根据实际应用情况选择。此外,由于天然气气体的成分较复杂,为方便用户使用,把所有组分参数输入设置在同一个界面上,组分默认值都设为0,用户可根据计算需要,填入相应的气体组分。由于每次用户输入量较多,系统设置了将用户的历次输入进行自动保存的功能,每次运行时系统会自动调出最近一次的输入值,也可找出历史记录,同时,用户可根据实际输入情况进行修改。 以某天然气的取样数据为例(见表1),将表中数据输入软件界面,点击“计算”按钮,便可得出试验工况和基准工况下的压缩因子和气体真实密度,结果如图3所示。 表1 天然气取样组分Table 1 Components of natural gassampling 图3 实例演算界面Fig.3 Interface of example calculation 以GB/T17747.2附录C中表C1中的1~6号气体取样数据为例[4],应用该软件对不同工况下多样本取样数据进行计算,计算结果如表2所示。与附录C中表C2所给结果进行对比,结果表明,该软件计算结果平均误差几乎为0,完全能满足工程实际应用的需要。 表2 计算结果与附录C中表C2结果的对比分析Table 2 Comparative analysis of calculation results and table C2 in appendix C 1)基于AGA8-92DC计算模型,将求解步骤进行模块分解,并探讨了算法流程,用弦截法对牛顿迭代算法进行优化,全面优化天然气压缩因子算法流程,提高了计算效率。 2)根据数学模型和算法流程,基于Visual Studio.NET开发平台,采用C#语言设计并实现了压缩因子计算软件开发,将核心计算模块封装成动态链接库形式,便于软件直接调用,同时将不变量进行缓存并可直接调用,具有良好的扩展性及安全性,便于二次开发,提升了开发效率和计算精度。 3)采用GB/T 17747.2附录C中的数据对所开发的软件进行验证计算,与GB/T 17747.2表C2结果进行对比分析,结果表明,该软件计算平均相对误差几乎为0,能满足工程实际应用要求。2 软件开发
2.1 软件设计
2.2 软件实现
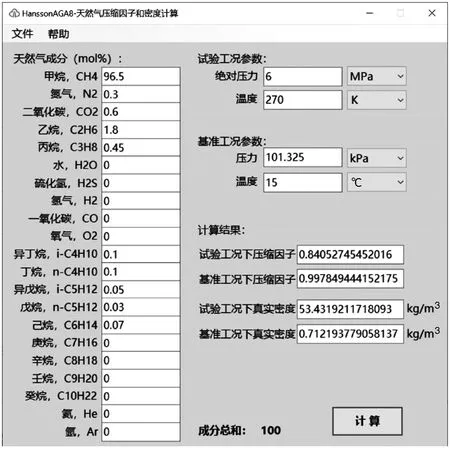
3 实例应用分析


4 结 语
