基于ANSYS和BPNN的开关柜温度场及温度预测研究
2021-03-17李少飞马兴明
李少飞,马兴明,杜 璇
(1.国网黑龙江省电力有限公司大庆供电公司,黑龙江 大庆 163458;2.上海博英信息科技有限公司,上海 201100)
0 引 言
温度是开关柜安全运行的重要指标,多数故障和异常现象可以通过热效应展现出来。由于开关柜内部机械和电气结构相对复杂,故障率较高,且故障主要为温度过高[1],如开关柜触头、电缆接头接触异常时,易发生局部过热。长期运行可能导致材料的机械强度下降,绝缘老化或击穿,造成供电中断,从而带来巨大的损失。
目前,开关柜的温度测量研究主要包括热路和温度场两个方向[2]。热路普遍采用热电类比的方法对电力设备进行热效应研究。丁健等[3]通过构建开关柜断路器触头的热路模型,分析接触电阻的影响因素,并提出热故障的预防措施。张敬菽等[4]建立了磁柱式断路器主回路的等效热网络模型,研究温升影响,并通过热网络模型可以修改电力设备参数,优化产品设计。
与热路方法相比,温度场分析的结论更加精准。同时,随着计算机技术和算法的不断进步,解决了温度场微分方程求解的难度问题,使得开关柜温度场仿真分析的方法得到广泛应用。宋帆等[5]建立了GIS隔离开关的三维有限元,分析模型的工频磁场,计及涡流损耗计算温升。张俊民等[6]采用壁函数方法处理固体与流体界面的对流换热问题,建立断路器三维模型,提出温度场和气流场计算方法。
该文应用热学传热理论和开关柜导热微分方程,对开关柜的温度场分布开展量化分析,可以确定易发热部位,进而开展温度实时监测和温度预测。不仅能够为开关柜的设计工艺改进和设备安全控制提供数理依据,而且可以提升开关柜的智能化水平[7]。
1 开关柜温度场分布
温度场分布主要是通过导热微分方程和单值性条件确定的微分方程组进行表述及求解。
1.1 传热机理
当空间内物体间存在温度梯度时,基于不同的热量传递机理,会产生热量传递,常见的方式包括热传导、热对流和热辐射[8]。
热传导定律表明了纯导热过程中热量在固体介质中的传递规律,可以表示成
(1)
式中:q为热流密度;T为温度;n为导热面积;λ为导热系数,与材料、密度等因素有关。
牛顿冷却定律揭示了流体分子间的热对流规律,可以表示成
Q=αA(Ts-Tf)
(2)
式中:Q为热量;α为对流换热系数;A为换热面积;Ts和Tf分别为固体表面温度和流体温度。
热辐射定律表明了物体的电磁波辐射规律,可以表示成
Eb=σ0T4
(3)
式中:Eb为单位面积物体的辐射能量;T为绝对温度;σ0为斯蒂芬-玻尔兹曼常数。
所以物体间热辐射传递的热量为
(4)
式中:A为高温物体辐射面积。
1.2 导热微分方程
导热基本定律表明了纯导热过程中热量在固体介质中的传递规律,热流密度正比于温度变化率,与能量守恒定律联立,采用微元法分析,可得
(5)
式中:τ为时间变量;ρ为物料密度;c为物料比热容;T为温度;qv为内热源强度。
当物性参数稳定时,可化简为
(6)
式中:α=λ/(ρc)称为导温系数,等式左侧为非稳态项,▽2T为扩散项,qv/λ为热源项。
无内热源时,qv=0,式(6)可简化为傅里叶导热微分方程:
(7)
当物体稳态导热时,非稳态项等于0,可化为泊松方程:
(8)
当物体无内热源且稳态导热时,qv/λ等于0,非稳态项等于0,可化为拉普拉斯方程:
▽2T=0
(9)
1.3 单值性条件
导热方程符合温度场问题求解的一般规律,当温度场模型发生变化时,需根据实际情况需要对特定条件加以约束,以求得温度分布唯一解。能够约束温度分布唯一解的单值性条件主要包括:
1)几何条件。该条件量化限定研究对象的外形尺寸,且影响坐标系选定和方程求解的难度。对于开关柜而言,其几何限定相对简单,可确定为长方体空气模型和导体模型。
2)物理条件。该条件主要反映了物体的热学属性参数。在开关柜温度场研究中,需考虑物性特征随温度变化而发生改变的情况,一般通过实验确定材料物性与温度的量级关系。
3)时间条件。该条件反映了稳态导热和瞬态导热时域特点。在开关柜温度场研究中,外界环境及内热源(导体通过的电流)时刻发生变化,故稳态导热只是理想情况,实际为瞬态导热研究,需明确开关柜电流的时域变化。
4)边界条件。该条件是对分析主体和运行环境的约束。开关柜温度场研究的边界条件包括空间和时间限定的温度、热流密度、热交换系数的分布和变化规律。
2 接触电阻
开关柜的相邻两段导体通常采用螺栓把接或梅花触头压接方式,实现电能传递。由于加工问题,接触面不可能完全贴合,所以实际上是通过电接触面上的微观小点相互接触并导通电流,相当于有效导电面积减小,电阻增大,从而更易发热,这也与开关柜实际运行情况相符。
接触电阻包含收缩电阻Rs和表面膜电阻Rb两部分。由于导电斑点,电流在狭小路径收缩通过,产生的附加电阻称为收缩电阻,且与导电斑点的面积成反比[9]。随着导电材料运行时间变长,金属表面发生氧化,生成可导电的氧化膜,从而产生额外的电阻,称为膜电阻。故接触电阻表达式为
Rj=Rs+Rb
(10)
电流流经接触电阻,会产生电压降落,引发温升,表达式为
(11)

3 开关柜温度场仿真计算
首先,采用SolidWorks构建开关柜的简化模型,然后将简化模型导入ANSYS,应用有限元分析功能对开关柜的温度场进行仿真计算。
3.1 开关柜SolidWorks建模
以某10 kV电源开关柜为例,建立SolidWorks三维模型,其结构见图1。由于原始模型的结构相对复杂,需要进行简化。原始模型去除外壳、操作杆、绝缘子及绝缘套管等部件,简化模型中只保留通电导体,空气等效成与开关柜等体积的长方体,简化模型只包含导体和空气两部分,如图2所示。

图1 开关柜三维结构示意图Fig.1 3D structure of switchgear

图2 简化后的开关柜导体及空气模型Fig.2 Simplified conductor and air model of switchgear
3.2 开关柜温度场ANSYS仿真
仿真过程包括材料属性等相关参数确定,网格划分,加载计算以及后处理等。采用有限元分析法对开关柜进行温度场分析,将连续求解的温度场域离散成许多互联的子域,将单值性条件带入导热方程,推导满足整个温度场域的平衡条件,从而获得离散的有限自由度温度分布。
开关柜的热量传递方式包括金属导体的热传导、导体表面热辐射和导体与柜内空气的对流换热,建立导热微分方程组,可表述为
(12)
(13)
(14)
式中:ρ为物料密度;cr为物料比热容;T为物体温度;T1为环境温度;τ为时间变量;k为导温系数;Q为交换热量;n为法线方向;σ0为斯蒂芬-玻尔兹曼常数;u为空气流速。
对于接触电阻的设定,将导电斑点等效成微小圆点阵列,通过修改电阻率方式模拟收缩电阻和氧化膜电阻,设置导电斑点电阻率为铜的100倍,如图3所示,物性参数见表1。
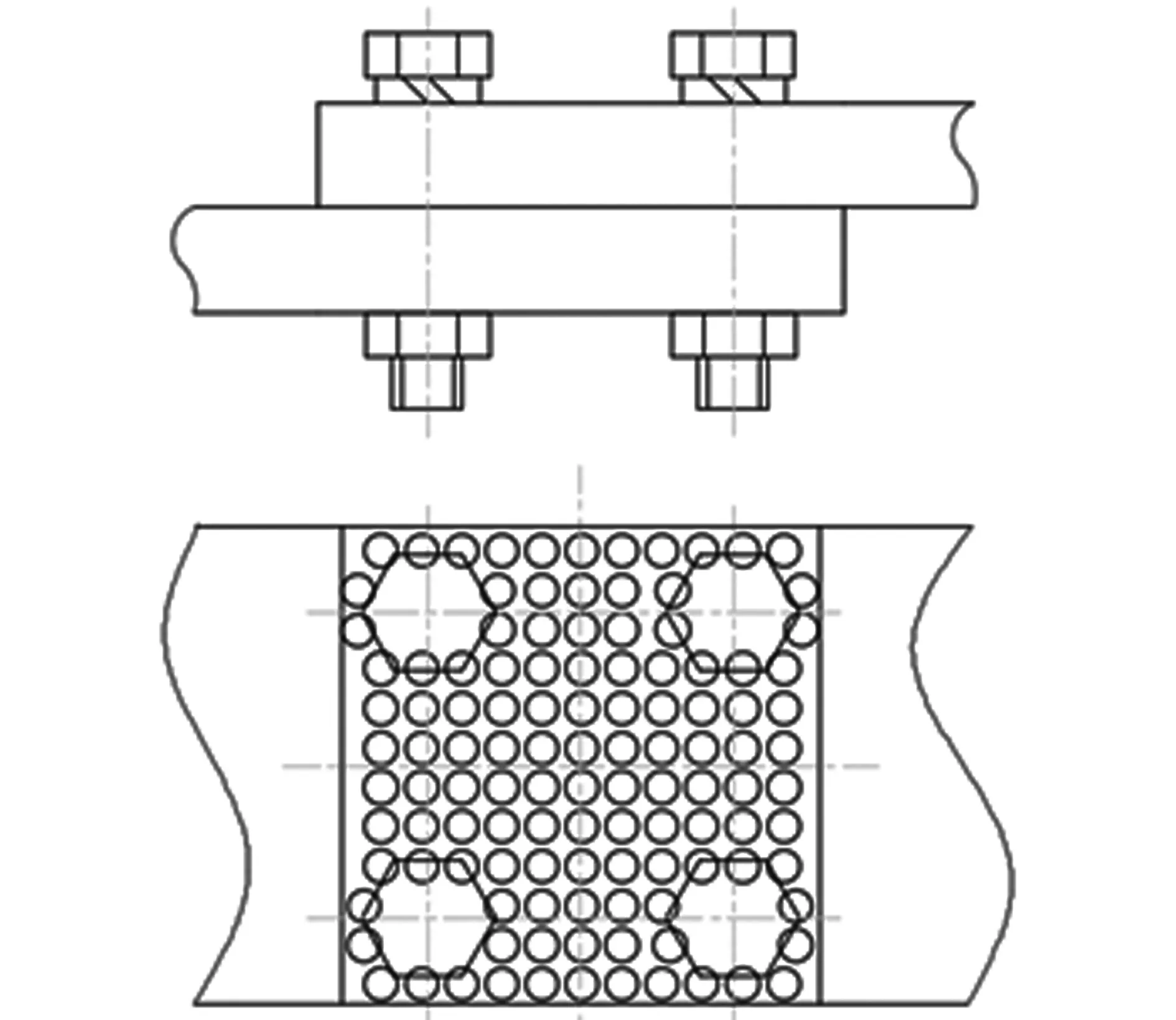
图3 接触面等效电阻模型Fig.3 Equivalent resistance model of contact surface

表1 物性参数表Table 1 Parameters of physical properties
考虑接触电阻的模型如图4所示,深色部分为接触电阻。
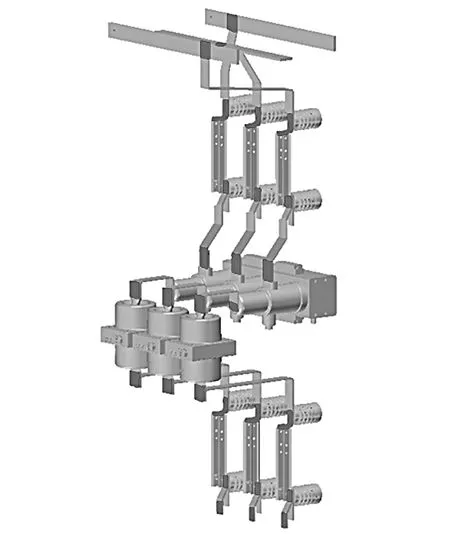
图4 考虑电接触时的实体模型Fig.4 Solid model considering electrical contact
采用扫掠方法,智能剖分导体和空气,定义合适的单元大小和长度,单元数量约为200万个。
根据经验,设定导体、绝缘体、空气和外壳的介电常数分别为200、3、1、200 F/m;设定空气与导体之间的热交换系数设为20 W/(m2·K);将空气的计算区域外边界温度设为25 ℃。之后给三相导体加300 A电流,获得导体温度分布,见图5。
图5中体现出,有接触电阻存在的导体部分及其附近区域的温度相对较高,这是因为触头部分附近的电接触较多,电接触是重要热源。
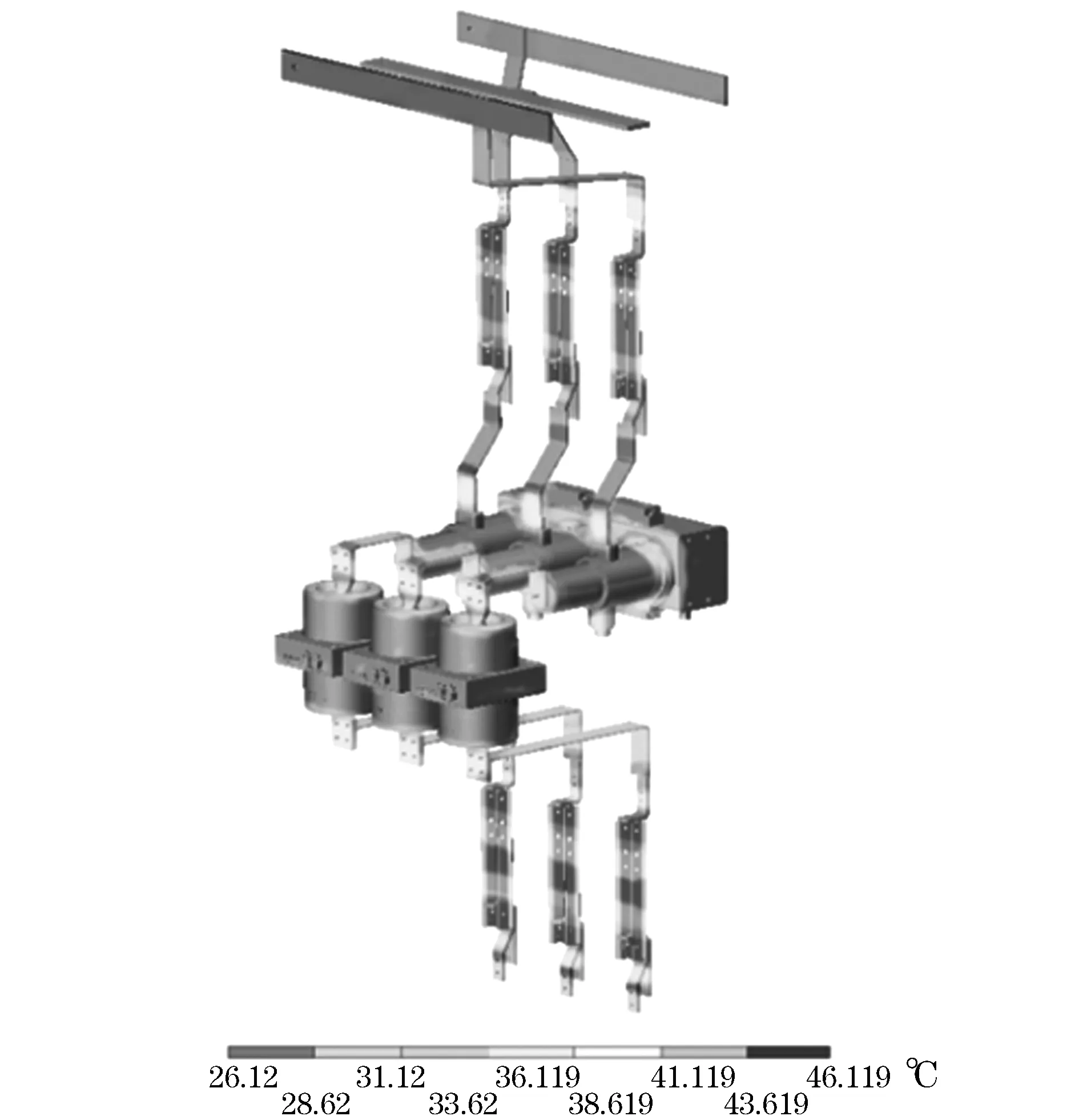
图5 导体表面温度分布示意图Fig.5 Temperature distribution of conductor surface
在实际测温操作过程中,受开关柜及温度传感器结构的影响,一些关键测点的温度不易测量,例如铜排搭接处和动静触头接触面。针对该类测点,采用的方法是测量相邻易测部位的温度,将该温度值等同于待测点温度。根据运维经验,选取1~10号测点为关键测点,其中1~9号测点受开关柜结构影响,温度不易测量。选取1′~9′号测点,位置临近关键测点,便于安装温度传感器,如图6所示。根据温度场理论,应用ANSYS对开关柜温度场进行仿真,同时采用红外测温法对以上测点进行实测。通过对比,验证仿真方法的精确性,结果如表2、图7和图8所示。
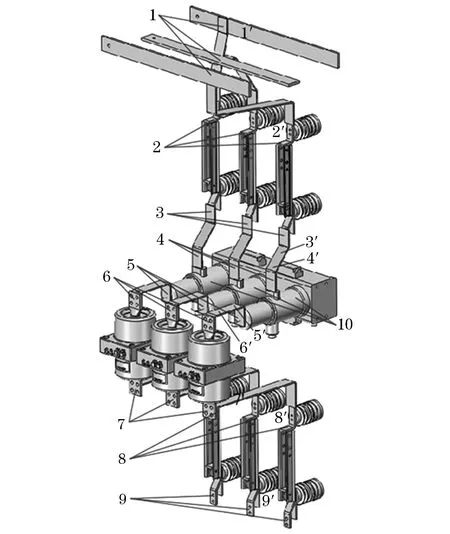
图6 开关柜测点示意图Fig.6 Schematic diagram of measuring points of switchgear
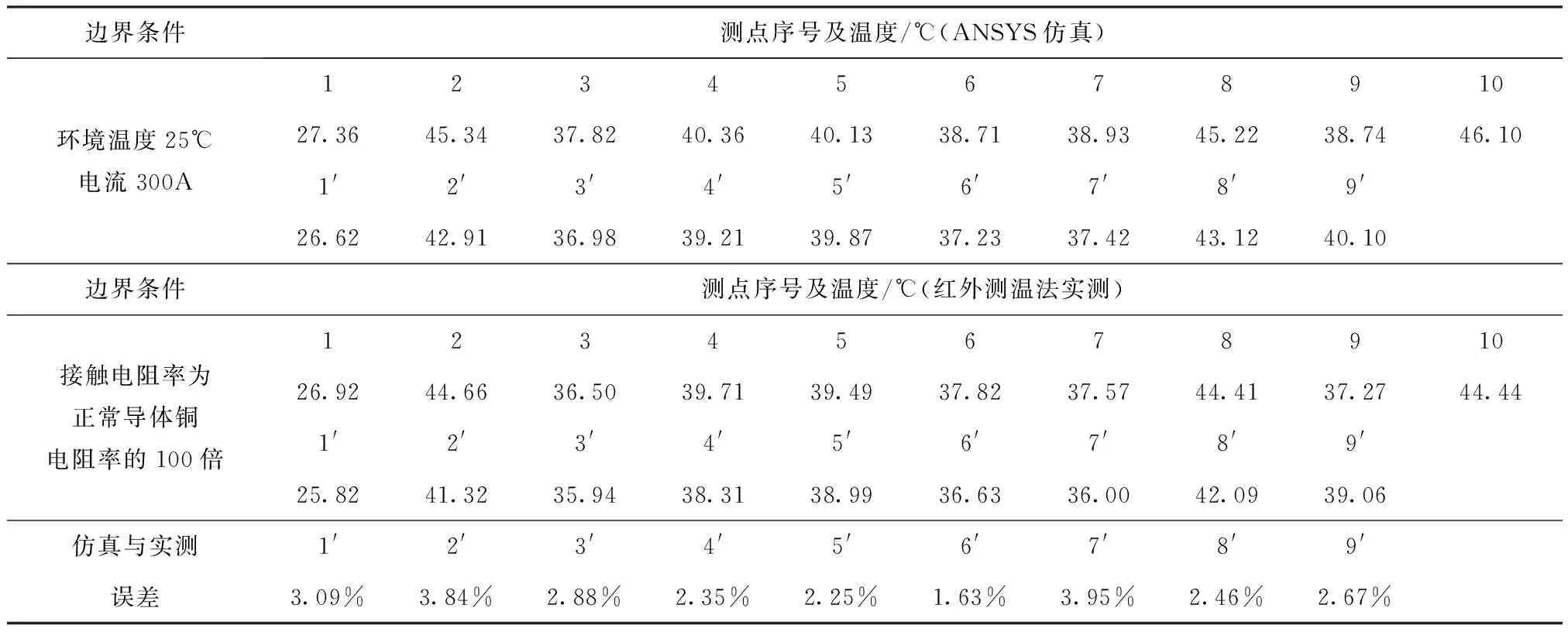
表2 开关柜温度场数据Table 2 Temperature field data of switchgear
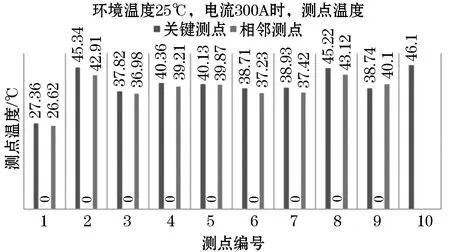
图7 关键测点和相邻测点温度分布图Fig.7 Temperature distribution of key and adjacent measuring points
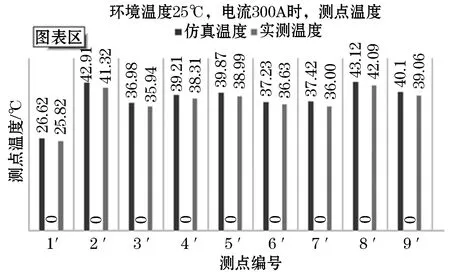
图8 相邻测点温度的仿真和实测数据对比图Fig.8 Comparison between simulated and measured temperature at adjacent measuring points
通过对比可以看出,关键测点与相邻测点的温度误差在2 ℃范围内,等效精度符合要求,对开关柜的安全运行更具有实际意义。使用ANSYS仿真与实测的最大误差为3.95%,平均误差为2.79%,仿真精度符合预期要求,从而验证开关柜温度场仿真方法的有效性。
4 关键测点温度预测
基于开关柜运行数据、环境温度和设备物性,采用BP神经网络(BPNN),形成关键测点和相邻易测部位温度的函数对应关系,通过测量关键测点的相邻易测部位温度,推算关键测点温度,为开关柜运维工作提供更加精准的温度数据。
4.1 神经网络
基于预测的准确性和收敛性,选择BPNN作为关键测点温度预测的实现方式。BPNN的结构如图9所示,是由若干具有数据处理能力的神经元构成了网络的输入层、隐含层和输出层[10]。

图9 BPNN结构示意图Fig.9 Structure diagram for BPNN
通过学习,BPNN的输入值和输出值形成确定的函数映射。首先,数据样本由输入层正向传播到输出层,生成的输出值和期望值之间会产生误差,然后BPNN将进行反向计算[11]。通过调整各层级间的权重,不断减小系统输出值和期望值的差值,反复进行正向和反向过程迭代,最终使输出值逼近期望值。
当BPNN完成学习训练时,将进入预测识别阶段,利用BPNN的输入输出映射关系进行开关柜关键点温度预测,其流程见图10。

图10 BP神经网络识别流程图Fig.10 Flow chart of BPNN identification
4.2 基于BP神经网络的温度预测
BP神经网络参数的设定影响预测的准确性和收敛性,经过多次试验分析,总结最佳的参数设置如下:
1)样本参数:每个测点各选取100组温度数据样本,60组用于BPNN的学习训练过程,40组用于关键测点温度预测识别效果。
2)网络层数:1个输入层代表开关柜温度特征量,包括测点编号、电流、环境温度和测点温度;1个输出层代表关键测点温度;1个隐含层既能保证预测精度,又能提高运算速度[12]。
3)神经元数量:输入层神经元的数量是开关柜温度特征量的数量,设置为4个;输出层神经元数量根据开关柜结构和运维经验,设置为关键测点的数量10个;隐含层神经元数量设置为4个。
4)初始化权重设置为-1和1间的随机值;学习速率设置为0.02;期望误差设置为0.01;最大训练次数设置为10 000次。
当环境温度为25 ℃,电流为300 A时,采用BP神经网络算法,基于图8中1′~9′号测点温度,预测1~10号关键测点温度,开关柜关键测点温度预测结果如表3所示。

表3 识别结果Table 1 Identification results
由识别结果可得,BPNN对开关柜关键测点温度预测平均预测误差为1.78%,总体预测精确度较高,验证了采用BPNN进行开关柜关键测点温度预测方法的可行性。
5 结 语
基于传热学研究,建立了开关柜温度场温度分布的导热微分方程,采用SolidWorks和ANSYS构建开关柜模型,并进行开关柜的温度场仿真计算。采用人工神经网络,对关键测点温度进行预测,验证了仿真模型和预测模型的准确性。所提方法不仅为开关柜运维工作提供更加精准的温度数据,而且为开关柜的设计工艺改进和设备安全控制提供数理依据[13]。
由于在开关柜温度场研究中,外界环境及内热源时刻发生变化,实质为瞬态导热研究,不仅需对开关柜电流的时域变化进行预测,还应对导热微分方程和开关柜仿真模型进行优化,细化单值性条件。同时,计及电磁场影响的开关柜温度分布在今后的研究工作中需进一步完善,进而提供更为精准的温度场预测数据。
