改进PSO算法在光伏阵列多峰值中的应用
2021-03-17宣丽萍张亚坤闫姝含
宣丽萍,张亚坤,闫姝含
(黑龙江科技大学 电气与控制工程学院 ,哈尔滨150028)
0 引 言
光伏微电网在局部阴影条件时,光伏阵列P-U曲线容易出现多峰值现象,相比较于传统MPPT(Maximum Power Point Tracking)算法,粒子群算法在解决连续函数极值类问题时有诸多优势[1-3],但容易陷入局部最优。通过正弦改进策略的动态惯性权重优化方式,可降低寻优时间[4]。惯性权重对粒子算法搜索范围影响较大,优化后粒子算法在早期给定较大惯性权重,增强全局寻优能力。算法后期减小,避免过早收敛于局部最优解[5]。将光伏微电源经BOOST电路升压,PI闭环调节后模拟最大输出功率。通过空间矢量脉冲调节,减少无功损耗,从而提高光伏电池的储能利用效率。
1 光伏微电网储能配置策略
1.1 光伏电池模
光伏阵列由大量光伏电池组串并联而成,因此先对光伏电池建模分析,图1为光伏电池等效模型。
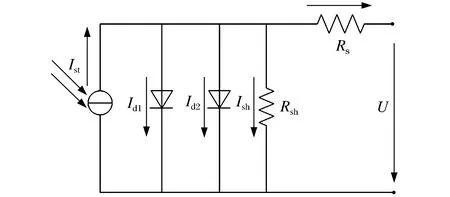
图1 光伏电池等效电路Fig.1 Photovoltaic cell equivalent circuit
光伏蓄电池在实际使用时储电效率受温度影响较大,其实际可用容量EBat与电池温度关系满足如下关系:
EBat=Estc[1+δ(TBat-TBat,stc)]
Soc(t)=(1-δ)Soc(t-1)+PBatΔtη+/EBat,N
式中:Estc为标准状态下蓄电池的额定容量;TBat为蓄电池在正常工作条件下温度;δ为光伏蓄电池的容量温度系数,通常情况下为6×10-3;EBat,N为储能系统的额定容量;η+、η-为储能系统的充、放电效率;TBat,stc为标准温度,一般默认值为25 ℃;Soc(t)为第t个时段结束时储能系统的剩余电量。
1.2 光伏阵列的多峰值特性
光伏阵列在温度不变、光照均匀条件下输出功率稳定。当并联中的部分光伏模块处于阴影下时,光伏阵列输出呈现出不同特性曲线。P-U特性曲线如图2所示,输出曲线呈现多极值特性。光伏电输出功率会出现多峰值与局部最大功率点。在Simulink中建模时,设置三种不同光照强度分别为 1 000 W/m2、850 W/m2、700 W/m2。光伏电池组在光照均匀时,P-U为单峰曲线,局部阴影时变为多峰值。

图2 不同辐照度下光伏电池P-U输出特性曲线Fig.2 P-U output characteristic curve of photovoltaic cell under different irradiances
2 改进粒子群算法在MPPT中的应用
粒子群优化算法(particle swarm optimization algorithm, PSO)通过设置惯性权重因子,更新位置与速度参数,寻找个体参数与群体极值。粒子群算法在光伏MPPT中处理局部最大输出功率效果良好,通过对粒子的迭代顺序和迭代方程进行改进,缩短全局搜索时间,避免PSO算法在MPPT中陷入局部最优。
2.1 PSO算法形式
PSO算法模拟鸟群的迁徙觅食群体特性,具有良好的鲁棒性和抗干扰性,可在多极值函数优化中寻找最优解。假设有N个参数,在n维空间中分散分布,每个参数只考虑位置xi与速度vi属性,其中速度表示当前粒子移动的快慢,位置为矢量移动方向。粒子在空间内搜索到自身最优解Pbest,t后,在空间粒子群内经算法分析,得到全局最优个体极值Gbest,i,经过n次迭代后在个体历史最优解中选择全局最优值,最终确定全局最优位置。迭代更新速度与位置下:
Gbest=max{f(Pbest,1),f(Pbest,2),…,f{Pbest,N}}
式中:w为粒子惯性权重系数,r1和r2为0至1范围内的随机数;N为粒子数;k为迭代次数;f(xi)为目标函数;c1、c2分别为学习因子。
通常在实际应用中,为防止算法失控,要对粒子的更新速度做一定的限制,通过调整惯性系数w和学习因子c1、c2,使这三部分互相平衡、互相影响,保证算法的寻优能力。改变场景时需要依据经验和实际情况对惯性系数w和学习因子c1和c2进行调整[6]。粒子群算法流程如图3所示。
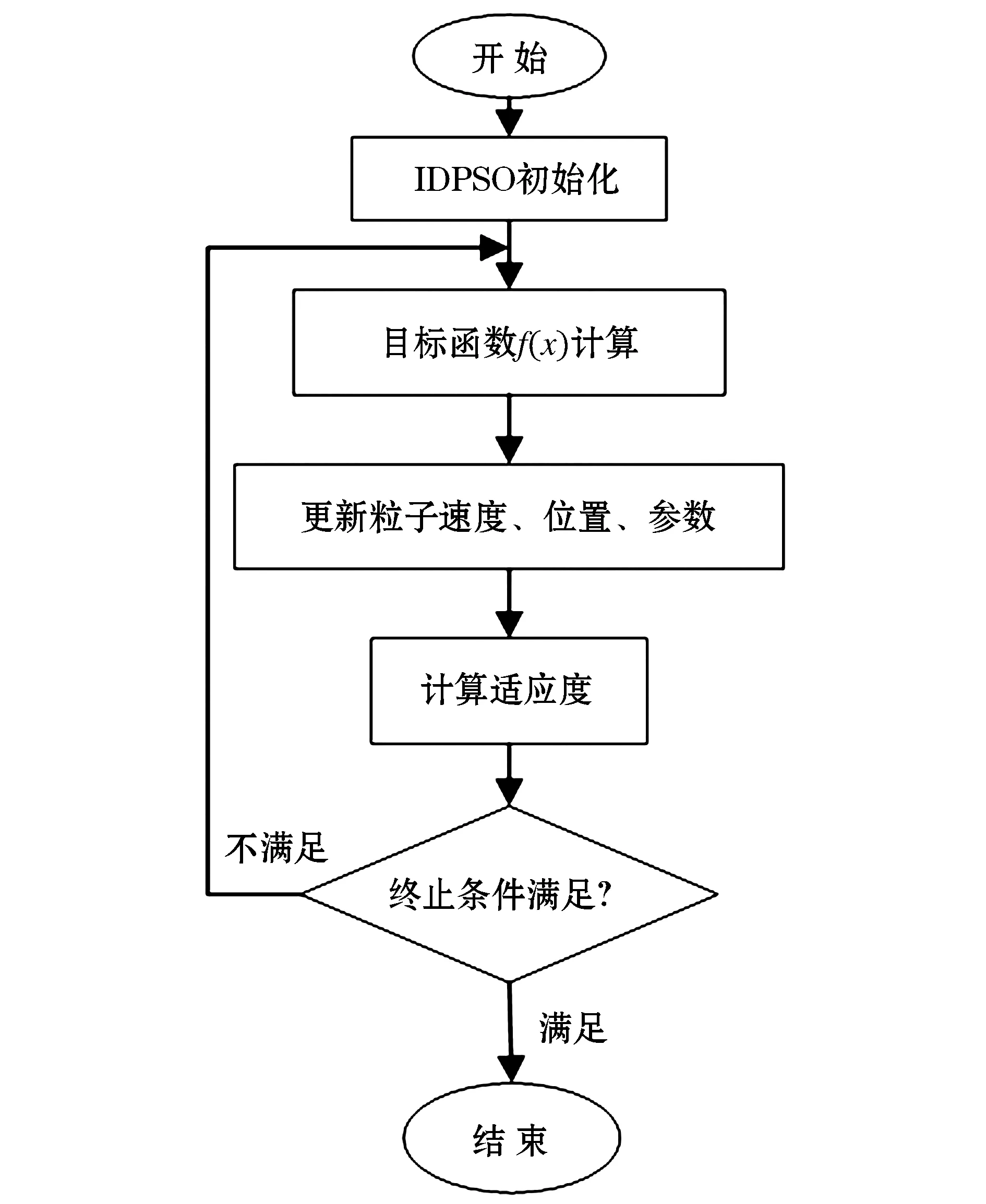
图3 粒子群算法流程图Fig.3 Flow chart of particle swarm optimization algorithm
2.2 改进PSO算法迭代过程策略
PSO每一次迭代都会更新出种群全局最优解以及其适应值大小,但各个粒子的适应值大小互不相关。在传统PSO算法基础上,引入基于正弦改进策略的动态惯性权重优化方法,利用正弦函数周期特性扰动粒子。将调节因子与正弦函数固定上下限配合,进而调整惯性权重ω值的浮动范围,调整粒子前中后期的收敛速度和探索范围,具体公式如下:
式中:Imax为粒子的最大迭代次数;ωmin为最小惯性权重值,i为粒子个数,i1=Imax/c;i2=Imax/c+2;多次仿真实验后取ωmin,1=0.5,ωmin,2=0.9;c为振荡周期数,文中取值为5,振荡周期参数可以调节惯性权重的上下限,使得粒子的惯性权重维持在固定的范围之间波动。Matlab建模仿真时,模拟初始种群数为500,最大迭代次数为150,ωmin,1≤ω≤ωmin,1+1,惯性权重维持在0.4至1.2之间。迭代后记录个体最优值,IDPSO寻优后仿真如图4所示。

图4 优化PSO算法寻优轨迹Fig.4 Optimal trajectory of PSO algorithm
由图4分析可知,函数出现多个局部最大值。群体极值经过位置更新与多次迭代后,粒子在0.23 s时出现最优解,最优值位置为(17.26,19.14),优化后PSO算法能实现在较短时间内获取最优值,该算法最终数据接近函数最优值。
2.3 PSO算法迭代过程策略
改进粒子群算法在MPPT中应用时,把光伏阵列的输出电流看作粒子,采用线性递减的惯性权重可以在提高算法收敛速度的同时获得较优的全局最优解,文献[7]通过设计参数和约束条件对PSO算法优化,但寻优时间较长。文中通过正弦改进策略的优化方式,使其输出电压与功率波动范围小,最大功率点寻优时间更短。具体公式如下:
ω2=ωmax
式中:ωmax为最大惯性权重值;f为当前粒子的适应值;favg为种群当前的平均适应值。当f≥favg时,惯性权重取最大值ωmax,粒子以较长步行参与全局搜索最优解,迭代次数减少,同时探索未知区域的能力增强,有利于粒子跳出局部极值[8]。
3 改进算法仿真分析
3.1 模型搭建
应用Matlab/Simulink搭建仿真系统,改进PSO算法搜索到光伏最大输出功率点Pmax后,将对应最大电压Umax经BOOST升压后输出值为最优电压。电路系统采用PI闭环控制,将光伏电压作为反馈,输出电压经空间脉宽SPVWM调制。与传统正弦波脉宽调制相比,输出交流电压幅值上升约15%,光伏MPPT控制电路如图5所示。

图5 光伏MPPT控制系统Fig.5 Photovoltaic MPPT control system
系统模块由光伏阵列、BOOST升压电路、电阻模块、MPPT控制器组成。在Simulink模型中增加了示波器和数据存储模块。操作时选取50个粒子,其初始位置均匀分布在电压区间内; 初始惯性权重w=0.85,最大迭代次数为150。将Matlab中的算法改进后并联BOOST电路,仿真如图6、图7所示。

图6 阴影下PSO 的功率跟踪结果Fig.6 Power tracking results of PSO in shadow
由图6可知,PSO算法在0.2~0.7 s时一度陷入了局部最优,1.3 s后成功跟踪到最大功率点,Pmax,1= 97.1 W,其功率波动范围为 96.8~97.3 W。改进正弦策略的动态惯性权重优化方式后,其输出功率如图7所示。

图7 改进粒子算法阴影功率跟踪结果Fig.7 shadow power tracking results of improved particle algorithm
由图7可知,在阴影条件下跳出局部最优。在0.9 s时追踪到了最大功率点Pmax,2=108 W,提高了有效输出功率与跟踪精度。功率跟踪误差小于1%,其功率波动范围在107.85~108.45 W之间。仿真实验表明,改进PSO算法能可靠追踪到最大功率点,容易跳出局部最优,从而提高光伏系统发电效率。
4 结 语
传统光伏阵列MPPT在部分遮阴影时,不能有效追踪局部功率极值。通过正弦改进策略的动态惯性权重优化方式,调节惯性权重与学习因子的自适应调节,优化PSO算法,使其不易陷入局部最优解。光伏电池经Simulink建模仿真后,与传统最大功率点追踪相比,该方法能加快收敛速度,提高系统效率。
