分裂四元数的伪相似性

唐哲，曹文胜

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言及预备知识

四元数是Hamilton 在1843 年提出的数学概念[1]. 记R 和C 分别表示实数域和复数域，则四元数可表示为：

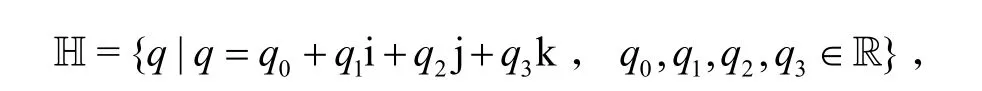
其乘法规则如下：

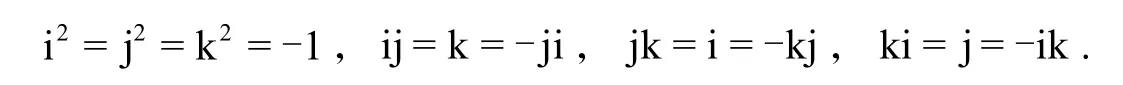
分裂四元数分析学和表示论在物理学里有重要的地位[2-4]. 1849 年，James Cockle[5]引入了分裂四元数其中一般地，认为 R=span ｛1｝和 C=span ｛1 ,i｝ . 根据分裂四元数乘法规则，一个分裂四元数可以写成：

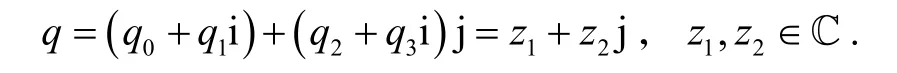
分裂四元数的I（q）可为正数，负数，也可以为零. 这与四元数的模长非负不同[6]. 此外，分裂四元数q的实部为： Re(q)=q0；分裂四元数q的虚部为：通过简单计算，得出I（pq）=I（p）I（q）.另外，定义q′：

很显然，I（q′ ）=I（q）. 与四元数类似，得到

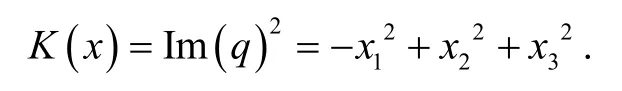
定义1两个分裂四元数a,b∈Hs是伪相似的，当且仅当存在使得

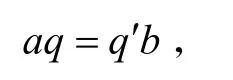
文献[1-7]研究了四元数、分裂四元数、分裂四元数的相似性，其中，曹文胜等[6]研究了分裂四元数a,b∈ Hs-R 是相似的充要条件. 本文将在文献[6]的基础上讨论分裂四元数的伪相似性.

2 分裂四元数的相关性质

分裂四元数代数 Hs通过下面的双射映射，可同构到矩阵代数 R4×4中.

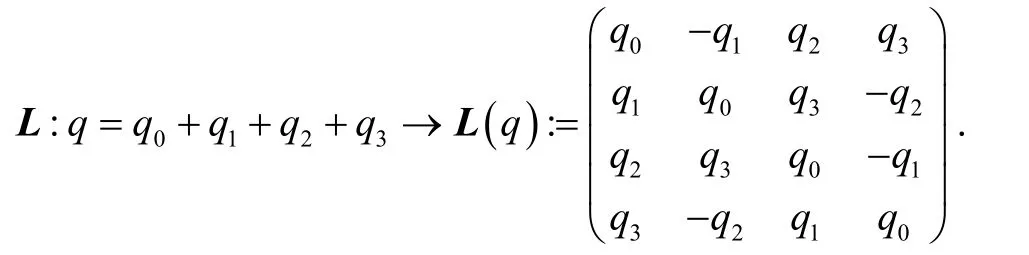
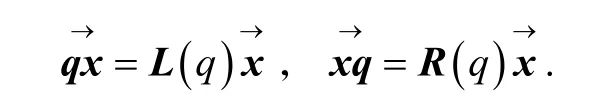
称L（q）为左乘矩阵，R（q）为右乘矩阵. 通过简单计算得：

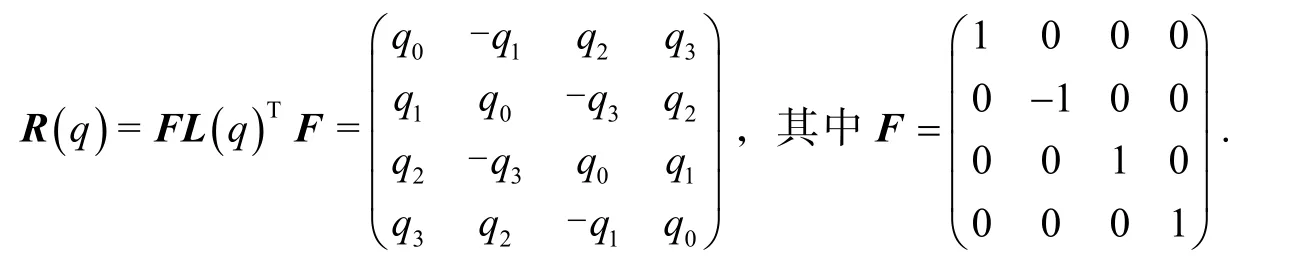
另外，F=FT=F-1.

3 分裂四元数的伪相似性

分裂四元数a,b∈ Hs是相似的，当且仅当存在q∈ Hs-Z（Hs），使得qa=bq. 分裂四元数a,b∈ Hs-R 是相似的充要条件[6]是：

由定义1 可知分裂四元数a,b∈ Hs是伪相似的，当且仅当存在q∈ Hs-Z（Hs），使得aq=q′b. 因为Hs不是一个除环，因此找到逆元来解方程ax=x′b就变得非常困难，故要先保证它存在非零解. 因为

所以方程aq=q′b等价于其中F=diag ｛1, -1,1,1｝.

通过计算验证下面命题.

命题1令S（a,b）=L（a）-R（b）F，其中

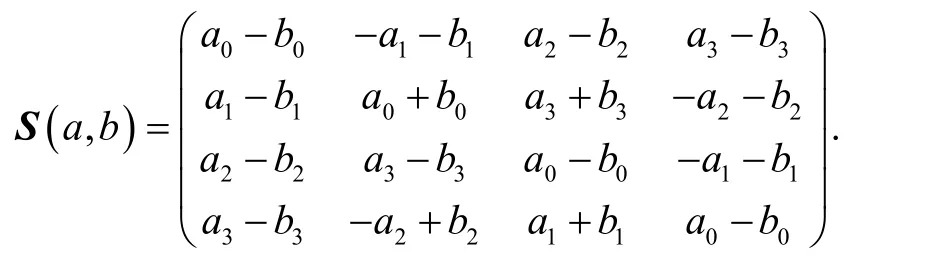
由此可知矩阵S（a,b）的特征值是：

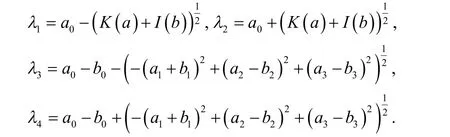
和矩阵S（a,b）的行列式是：

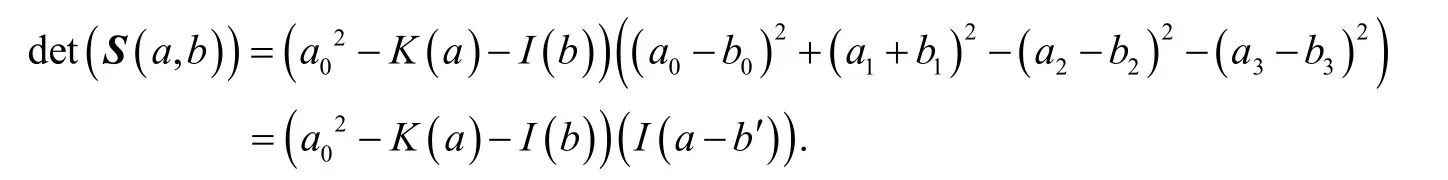
进一步， det （S（a,b））=0当且仅 当如下的情形成立：

下面列 举几个行列式 det （S（a,b））=0的例子.

1）a=2+3i+4j +5 k,b=2 - 3i+4j+5k,a-b′=0.

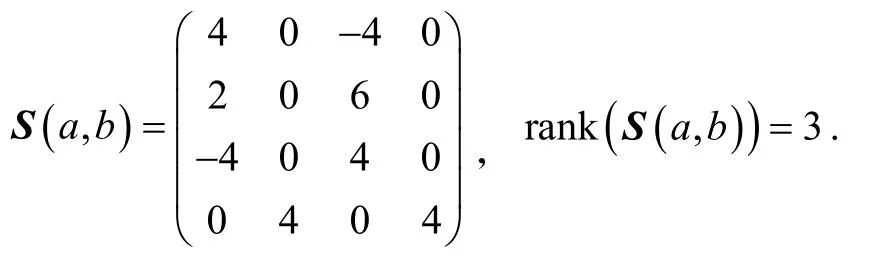
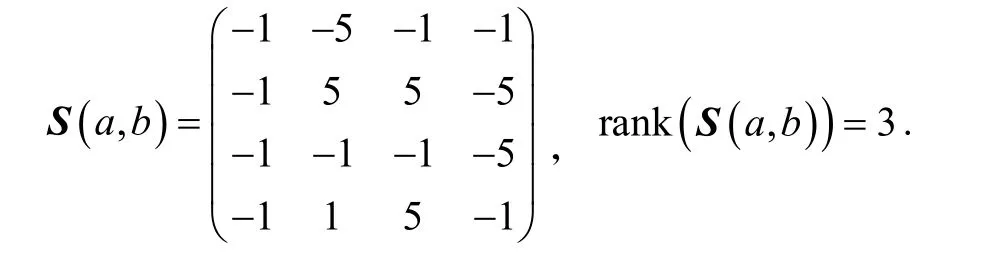
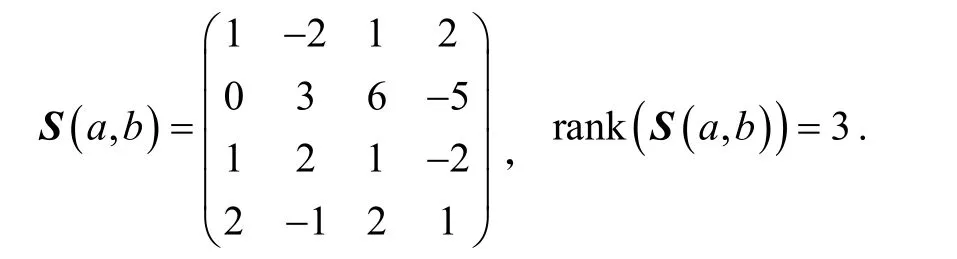
定理1分裂四元数a,b∈ Hs-｛0｝是伪相似的充要条件是下面二个条件之一成立：

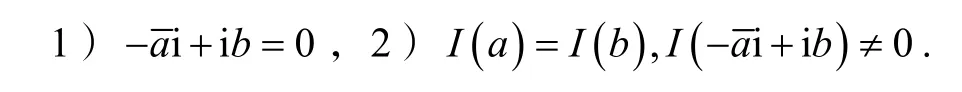
证明令并且a,b不为零.如果a,b是伪相似，那么存在一个满足有所以，故因为这表明：