从“无身”到“具身”：高中数学课堂的转向

【摘 要】高中数学课堂实现“无身”到“具身”的转向，需要在课堂导入中从“无身”到“具身”，实现学习的实践转向;在知识生成中从“他心思考”到“具身心智”，实现思维的嵌入转向;在知识的联结与发展中，从“浅层学习”到“深度学习”，实现学习的价值转向。

【关键词】“无身”;“具身”;浅层学习;深度学习

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2021）88-0033-04

【作者简介】张阳，江苏省吴江区教研室（江苏苏州，215200）教研员，高级教师。

当前的数学课堂教学，教师在设计教学时重视问题的引入、数学意义的建构和数学知识的应用，特别注重教师传递知识的过程，却忽视了学生的内化过程及具身参与。

具身教学强调身体的核心作用，重视身体与环境的相互作用。具身认知与数学课堂教学有着很好的契合点，它重视学生学习端的供给侧，重视知识的体验性、人本性、生成性。[1]

一、從“无身”到“具身”，实现学习的实践转向

无身教学关注知识传递，漠视学生的知识生成过程。而教学的本质是促进学生全面发展，帮助学生挖掘自己的特质，实现个体价值。这一切都建立在学生能对自己进行清晰分析与定位的基础上，需要学生在体验中品味知识、认识自己，在活动中扩充知识储备。因此，教师要在教学中设置具身情境，引导学生参与其中，通过肢体参与刺激其心智参与，促成身与心的融合。下面，笔者以人教A版必修一第五章第一节“任意角”一课的课堂导入片段为例，说明设置具身情境对引导学生学习实践转向的重要作用。

教学片段1：“任意角”的课堂导入

活动1：请同学们课前准备一瓶纯净水，先后将水瓶拧开与拧紧，观察拧开与拧紧过程中拧瓶盖的方向与圈数，用文字语言描述操作过程。

生1：拧开需转动瓶盖1周半。

生2：拧开与拧紧的方向不同，拧开是逆时针方向，拧紧是顺时针方向。

【设计意图】由生活中的实例导入，每名学生都可以操作体验，让知觉、视觉等身体感观直接参与学习过程。引导学生用生活化的语言描述具身体验的过程，有助于提升学生学习的兴趣。

活动2：请学生利用已经学习过的数学知识，用数学语言描述两种操作。

生3：旋转360°+180°。

生4：旋转540°。

生5：角的最大度数是360°，没有540°。

生6：540°不对还有一个原因。拧开与拧紧的度数是一样的，但方向不同，没有将两种行为区分开来。

【设计意图】引起学生的认知冲突，使学生回忆初中所学的角的概念，主动用数学知识解释生活现象。

活动3：安排学生进行小组讨论，回忆初中所学的角的概念，讨论此概念能否解决拧瓶盖的角的度数的问题。

组1：没有办法解决，我们所学的角的概念是“从一个顶点出发的两条射线组成的几何图形”，这个概念无法描述旋转。

组2：我们初中所学的角的度数范围是0°到360°，拧瓶盖现象已经超过这一范围。

师：如果要用数学概念对拧瓶盖现象进行解释，就需要我们重新定义初中所学的角的概念。请同学们继续分组讨论，如何改造角的概念，才可以合理地解释拧瓶盖现象。

【设计意图】学生自主探究并理解新的概念，是具身课堂的特征。教师在教学过程中帮助学生回忆已有的知识体系，从具身实践开始，让学生深入探究学习、构建新知。

上述教学活动使得学生在实践操作的过程中融入感觉、知觉等身体感知，再用数学语言抽象出行为的特征，得出概念。

二、从“他心思考”到“具身心智”，实现思维的嵌入转向

“他心思考”即我们如何知道他人对待事物的思维、情绪与经验。在教学中，教师常预设学生在学习时会遇到哪些困难，并思考如何处理这些困难。在实际教学中，教师的预设可能是正确的，也可能存在错误。“以己度人”的他心教学可以帮助部分学生解决知识内化过程中产生的困惑，而一些教师往往会重视与自己预设相同的回答，忽视不同的观点和具有思维发散性的回答，这就导致有些学生的困惑没有得到解决与回应，进而影响其学习的深入度与知识掌握的程度，同时也不利于学生学习思维的发展。

为解决这一问题，教师可以在课堂上安排学生小组讨论。通过分组讨论，组间辨析，组内消除异议，学生达成共识，提炼出共性问题，随后教师对这个共性问题进行释疑解惑。学生在达成共识的过程中，充当了教师的角色，针对每个人的问题互相解释、共同进步，有助于迅速理解问题、解决问题。

教学片段2：“任意角”的新知生成

活动4：如果用数学知识解释我们拧开与拧紧瓶盖的过程，同学们认为应该怎么样扩充角的概念呢？

生1：角的概念要加入旋转。

生2：角的范围需要改变，以前的0°到360°已经不适用拧瓶盖现象。

师：同学们的建议很好，还有没有其他需要考虑的问题？

生3：初中所学的角是静止图形，需要定义成运动的概念，还要定义旋转的不同方向。可以加入正负，来区分角旋转的方向。

师：请同学们用文字语言描述对角的概念的新定义。

生4：角是由一条射线绕着它的端点旋转所成的图形。

生5：正角，一条射线绕其端点按逆时针方向旋转形成的角;负角，一条射线绕其端点按顺时针方向旋转形成的角;零角，一条射线没有做任何旋转。

【设计意图】概念的生成过程影响学生对知识的理解深度。特别是对于最基础的概念，让学生全程参与对其内涵外延的梳理，完成从具身体验到具身思维的过程，有助于实现概念的数学抽象化，为进一步学习提供理论上的支持。

活动5：让学生分组讨论，列举生活中关于角的现象，并用角的新概念解释这些现象。

组1：时钟分针的调节——①调快10分钟;②调慢10分钟;③调慢1小时10分钟。分别可以解释为分针旋转①60°;②60°;③420°。

组2：游乐园的摩天轮顺时针旋转了两周半，可以解释为摩天轮旋转-900°。

组3：跳水运动员，空中翻转三周半（顺时针），对应的解释为跳水运动员空中旋转-1260°。

【设计意图】高中学段的数学知识兼具抽象与直观两种特征，教师需要依据这些特征进行教学设计。此环节中，教师引导学生归纳出抽象的数学知识，再安排学生分组讨论，联系生活实例，加深了学生对角的新概念的理解，在教学中培养了学生发现问题、提出问题、分析问题、解决问题的能力，引导学生在生活中自觉运用数学知识。

三、从“浅层学习”到“深度学习”，实现学习的价值转向

浅层學习是指在外力驱动下，采用简单记述、重复训练和强化记忆的方式习得新知识的学习形式。[3]深度学习则注重学生的探究过程与批判理解，注重知识的迁移与运用。无身教学突出选拔功能，具身教学则注重教学价值的升华。具身认知下的课堂引入与知识生成应该简洁明了，迅速切入主题。

教学片段3：角的概念与已有数学知识的联结

活动6：全新的角的概念的数学特征是什么？

生1：是运动变化的几何图形，其运动方式为旋转。

生2：相同大小的角由于摆放位置不同，会呈现出不同的形态，怎么解决呢？

师：这个问题非常好。下面请同学们小组讨论，有什么办法能够处理运动变化的几何图象？

组1：函数的图象也是变化的，我们是借助坐标系描绘函数图象的。可以引入坐标系，解释几何图象的变化。

组2：可以对角进行规定，让它的顶点与坐标原点重合，始边与x轴正半轴重合，这样就将角的形态固定了。

在此基础上，教师可提供相关例题，供学生练习，巩固对概念的掌握和运用。

例：（概念辨析）下列说法是否正确，如果正确请说明理由，如果不正确请举出反例。

（1）锐角一定是第一象限角，第一象限角一定是锐角;

（2）所有角都是象限角;

（3）第二象限角比第一象限角大;

（4）终边相同的角大小一定相同。

【设计意图】数学新概念的内化可以从两方面入手：一是概念辨析，二是利用新概念解决旧问题。此环节中，笔者引导学生将角的概念与函数图象的知识相结合，加深学生对角的概念及性质的理解，引导他们自觉使用新概念和新知识解决问题。

教学片段4：角的概念与后续将要学习的数学知识间的联结

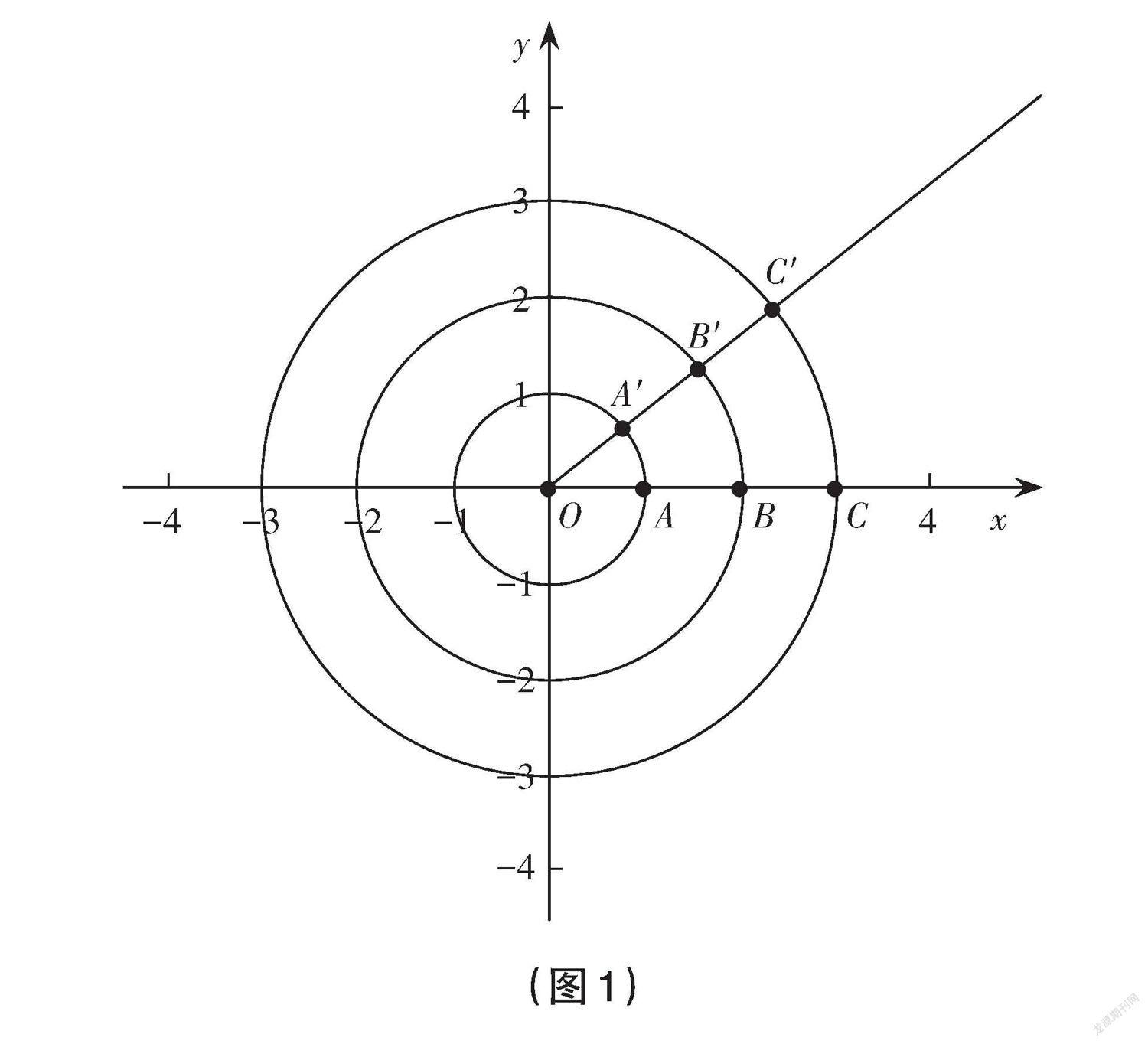
活动7：如图1所示，将角的顶点与坐标原点重合，始边终边都与x轴正半轴重合，在终边上取不同的点A、B、C，满足OA=1，OB=2，OC=3，将终边从初始位置按逆时针旋转角度θ，A、B、C所经过弧长分别为多少？它们与A、B、C三点的位置有关吗？

生1：离原点越远，点所经过的圆弧长越长，它们之间存在固定关系。

师（追问）：生活中有哪些现象与上述情形类似？

生2：自行车轮毂上的反光片转动时的行程，摩天轮上座位的行程。

【设计意图】具身认知下的深度学习，探寻数学知识由何产生、如何运用、有何价值，为下一阶段的学习奠定理论和方法论基础。教学片段4为下一步学习“弧度制”打下基础，将后续要学习的知识前置，加强了知识之间的关联性，同时也为学生构建知识体系、形成知识网络铺路，提高学生综合解决数学问题的能力，发展其数学核心素养。

深度学习有利于促进学生对教学内容的理解，促进知识体系的深度联结，并自觉运用知识进行理解、创新、实践。同时，具身认知在现实教学中的应用也对教学过程、教师和学生提出相应的要求：教学过程要清晰，目标明确、流程简洁;教师要以学生的视角进行教学设计;学生作为课堂的主体应积极参与教学活动，在课堂学习中不断发散思维，实现深度学习，并将所学知识运用于生活实践，真正实现从无身到具身的课堂转向。

【参考文献】

[1]张阳.具身认知：让数学现象教学从模糊走向清晰[J].江苏教育研究：理论版，2020（28）：3-6.

[2]束海波.他心知问题的现象学与认知科学解答[J].皖西学院学报，2016（5）：115-119，151.

[3]杨子舟.从浅层学习走向深度学习[J].教育探索，2016（7）：32-35.

本文系江苏省教育科学“十三五”规划重点资助课题“基于‘具身认知’观念，提升学习深度的高中数学教学实践研究（B-a/2020/02/12）”及江苏省教育科学“十三五”规划2018年度课题“高中生数学批判质疑能力的实践研究（B-b/2018/02/56）”的研究成果。

3466500589280