抓住数学本质 引发深度思考

郭利锋

[摘 要]不论是研究数学教材、数学教学，还是数学学习，都要善于透过现象抓住数学知识本质。在“乘法分配律”的教学中，运用联系的观点和思维，借助数與形、知识的关联与迁移，去发现、表征、解释、深化、拓展和应用规律，使学生的思维不但有深度，还有广度，让数学学习变得绚丽多彩。

[关键词]数形结合;正向迁移;联系;解释;深化;拓展

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）05-0057-03

乘法分配律是小学阶段一个非常重要的运算定律，但乘法分配律的内容和外在形式都比较复杂，不易归纳总结和理解掌握，更重要的是乘法分配律变式多、拓展多，应用范围广，因此乘法分配律的教学历来是教学的重点也是难点，还是学生考试的失分点。笔者经多年的实践研究得出：教师要有统观整个小学数学教材的意识，从系统、联系的视角分析和研究教材，确定“乘法分配律”的教学既是前面所学知识的概括总结，也是今后把整数的乘法分配律拓展到分数、小数中的“种子课”;在借助具体的情景从乘法的意义去理解和发现规律后，重点引导学生充分利用数形结合思想逆向验证和解释规律，同时打通乘法分配律与旧知之间纵向与横向的联系，抓住知识之间的共性和本质，并通过缜密的分析推理将规律迁移、拓展。因此，教师的教学不能仅仅满足于引导学生自主探究后推导出规律，要在推导出规律后从以下三方面解释、深化和拓展规律。

一、巧用数形结合，解释规律

“数”与“形”本来就是数学的两种基本形态，“数无形时少直觉，形少数时难入微”，描述的就是数和形之间的相互依赖关系。数形结合既是一种重要的数学思想，也是一种重要的教学方法和教学策略。教学“乘法分配律”时，要充分利用 “数形结合”的教学思想与策略，在引导学生探究规律时，按照“直观图形（形）——数字表示规律（数）——字母表示规律（模型）”这个顺序，遵循由具体到抽象的思考过程，帮助学生发现规律、归纳规律、建立模型。在得出规律、建立模型后，又可以通过反问、追问的形式引导学生按照“数字表示规律（数）——直观图形（形）——字母表示规律（解释模型）”的顺序，由抽象到具体再到抽象的反向思维来解释和验证规律的合理性。

【教学片段1】

师：乘法分配律左右两边为什么会相等呢？能结合4×9+6×9=（4+6）×9这个等式说明乘法分配律是成立的吗？请独立思考，把你的想法记录在学习单上，再在小组内交流讨论。

生1：我可以举例。我到文具店先买了4支钢笔，发现不够，又买了6支钢笔，每支钢笔的价钱是9元。要求一共用的钱数，可以先求4支笔的钱数和6支笔的钱数，再合起来就是总钱数，4×9+6×9=36+54=90（元）;也可以先算一共买了4+6=10（支），再求10支钢笔的总价，（4+6）×9=90（元），所以4×9+6×9=（4+6）×9。

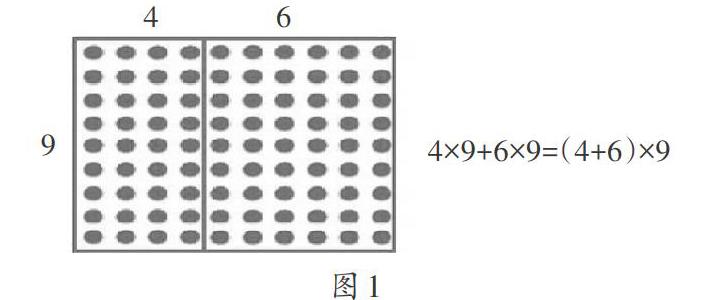
生2：我用点子图说明（学习单提供了点子图）。这个点子图有9行10列，我先圈4个9再圈6个9，合起来就是4×9+6×9，也可以按大的点子图来算是10×9，也就是（4+6）×9，所以4×9+6×9= （4+6）×9。（教师出示图1）

师：这两个同学回答得非常好，能够从不同的角度来解释乘法分配律是成立的。

师：如果我把这个点子图抽象成长方形，谁能用长方形的知识解释4×9+6×9= （4+6）×9是成立的？

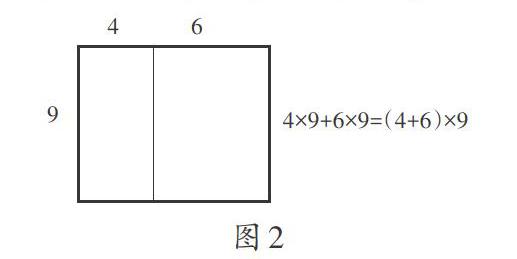
生3：4×9和6×9分别算的是两个小长方形的面积，合起来就是整个图形的面积; （4+6）×9是把两个小长方形看成一个大长方形来算，（4+6）是大长方形的长，所以4×9+6×9= （4+6）×9。（教师出示图2）

师：长方形的长和宽还可以换成其他数吗？可以换成哪些数？

生4：可以换成任何一组合适的数，比如8、12、18，8×18+12×18=（8+12）×18，也可以换成40、60、90，40×90+60×90=（40+60）×90。

生5：还可以用字母来表示。

师：今后用到乘法分配律，脑子里就要有这个图形，既直观好记，也容易理解。规律中的a、b、c三个字母不仅可以是整数，也可以是分数和小数，这是我们后面将要学习的内容，有兴趣的同学可以课后了解。

学生先从解决问题和乘法的意义去解释等式成立，再利用点子图直观说明了等式也是成立的。此时，教师再把点子图抽象成长方形，引导学生从求长方形面积的角度去说明乘法分配律是成立的，既直观好记也容易理解（如图4）。长方形面积与乘法分配律貌似不相关，但它们的本质内涵是相通的。充分运用数形结合和逆向求证的教学策略，能沟通“数”与“形”之间的关联，抓住数学本质，促进学生深度思考，帮助学生深层次理解和掌握规律。

二、打通知识的关联通道，深化规律

教师在引导学生的过程中，既要纵向透视，也要横向沟通，由点入线、线入面、面入体，把新知置于旧知网络体系中，寻找新旧知识之间的本质与共性，建立结构联系。这样的数学学习活动不仅有利于学生全面深刻地理解数学知识，而且有利于学生对数学知识的整体认识和宏观把握，养成良好的思维习惯。

【教学片段2】

师（出示图5）：其实，“乘法分配律”并不陌生，它就在我们身边。观察这些计算过程，你发现了什么？

生1：这些计算都运用了乘法分配律。

师：请具体说一说在计算中是怎样运用乘法分配律的。

生2：计算21×26时，可以把21分成20和1，先算20个26和1个26，再加起来就是21个26。

生3：计算114×21的道理也是一样的……

师：这些计算过程实际就是今天学习的乘法分配律的运用过程。

师：还有哪些旧知识用到了乘法分配律？

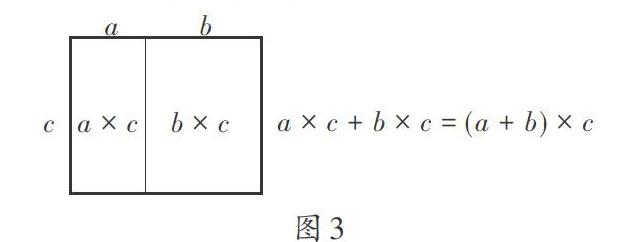
生4：长方形的周长公式也可以用乘法分配律来解释。因为长方形的周长就是四条边的总和，长×2+宽×2和（长+宽）×2都是求长方形的周长，所以长×2+宽×2=（长+宽）×2，用字母表示就是a×c+b×c=（a+b）×c。

师：同学们非常棒！学习数学就是要多观察、多思考、多反思，做个“有心人”。

这个教学片段以“乘法分配律”为纽带，通过设问引导学生把二位数乘一位数的口算和笔算、两位数乘两位数、三位数乘两位数和长方形的周长等知识串联起来，借助新知重新审视旧知，打通新旧知识之间的关联通道。借助乘法分配律的多元表征，抓住表征背后的本质内涵就是乘法分配律的运用，这不但让学生意识到乘法分配律应用的广泛性和重要性，也使学生感受到乘法分配律并不那么难学难懂，其实一直在运用乘法分配律解题，只是现在才加以概括和归纳，从而深化对规律的理解和掌握。

三、顺应知识的正向迁移，拓展规律

正向迁移是指在学习中获得的一种知识与学习经验对后续学习的影响，也就是常说的触类旁通、举一反三，“乘法分配律”这节课的最后一个练习就是利用知识的正向迁移对规律进行拓展应用。

【教学片段3】

出示：

师：淘气和笑笑是怎么想的？你会选择哪一个算式计算？为什么？

生1：淘气是先算一套衣服的价钱，再乘以28，笑笑是分别算出28件衣服和28条裤子的价钱后再加起来，方法不同，但都是算出28套衣服的总价。

生2：肯定都会选择淘气的方法，因为用淘气的方法两步就解答出来了，而且括号里的和是100，这样非常好算，口算就能得到结果，而笑笑的要三步，也没有那么好算，运算量大。

生3：这两个算式用等号连起来实际就是运用了乘法分配律。

出示：（46+54）×28 = 46×28+54×28。

师：为了更好的表演效果，学校决定给每个同学再买一顶帽子，怎么列式？

出示：

生4：（46+54+23）×28 = 46×28+54×28+23×28。

师：如果再加一双鞋呢？

出示：

生5：（46+54+23+57）×28 = 46×28+54×28+23×28+57×28。

师：仔细观察这三组等式，你有什么发现？

（46+54）×28 = 46×28+54×28

（46+54+23）×28 = 46×28+54×28+23×28

（46+54+23+57）×28 = 46×28+54×28+23×28+57×28

生6：計算等号左边的式子比计算右边的式子少算一步，计算起来要简便一些。

生7：括号里面不管是两个数相加，还是三个数或者四个数相加，加起来的和再乘以28，与28分别乘以这几个加数再相加的和，结果相等。

师：如果括号里面是更多的数相加，还有这样的规律吗？这个规律是什么？

生（齐）：有，是乘法分配律。

师：也就是说，乘法分配侓中“两个数的和”换成“三个数的和”“四个数的和”……乘法分配律也是成立的。

出示：（A+B）×Y = A×Y+A×Y

（A+B+C）×Y = A×Y+B×Y+C×Y

（A+B+C+D）×Y = A×Y+B×Y+C×Y+D×Y

……

师：同学们真了不起呀！这真是一个伟大的发现！也是一种很有价值的思考。

师：如果括号里的“+”改成“-”，规律还存在吗？这又是一个全新的猜想，由于时间关系，这个问题留给大家课后研究。

教师在巩固和内化规律后，引导学生把乘法分配律拓展到“多个数的和与一个数相乘”的探索。因为学生有了之前探索规律的经验，借助“合唱队买服装”的情景，学生得到结论就是水到渠成的事情。下课前的追问，让学生思考乘法分配律是否可以拓展到“两个数的差与一个数相乘”，后续练习还可以鼓励学生探索乘法分配律拓展到“几个数加减混合与一个数相乘”是不是也成立，甚至可以联想 “除法里是否也存在类似的规律？”。教师要善于运用知识的正向迁移对规律加以延伸和拓展，引发学生深度思考，学生的思维才会向深处扎根、向远处攀升，思维之花才会开得更加灿烂绚丽。

总之，数学知识是一个动态的、有生命力的知识体系，不管是教师的“教”还是学生的“学”，都要统观知识的整体，用动态的、发展的眼光紧紧围绕数学知识本质，挖掘知识的“昨天”，紧握知识的“今天”，拥抱知识的“明天”，才能帮助学生构建一个生态的、丰富的知识结构，学生的知识大树才会根深蒂固、枝繁叶茂。

（责编 金 铃）