数学概念是否可以自创

方艳燕

[摘 要]数学是严谨的，一些重要概念都是经过几代数学家审定和历史考验留下的精华，不容随意更改。但是，数学又是灵活机动的，变化万千，可以在不违背数学本质规律的基础上提出一些新概念，以提升课堂教学效果。

[关键词]数学;概念;自创

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）05-0032-02

偶然读到一篇数学教研论文，题为《老师，请不要“自创”概念——从“把分子通分”说起》，文中阐述了三种观点。1.“把分子通分成一样再比较大小”这种说法是错误的;2.在《初等数学辞典》及《中学数学教师手册》中关于通分概念的表述完全一致，即运用扩分的方式，把分母不相同的几个分数化成分别和原来的各个分数相等并且各分数的分母又彼此相同的分数，这种几个分数的等值变形过程叫作通分;3.通分还有一种基本定义：把甲数与乙数之比、乙数与丙数之比，这两个不同的比，化成甲与乙与丙之比，也叫作通分。如果通分只限于对分母“动手术”的话，那么第3点就应该无法成立;如果第3点可以成立，通分的概念就必须拓展，即“几个分数的等值变形过程”。按照这种表述，对分子进行通分也是通分，为何要区别对待，厚此薄彼呢？追根溯源，它们都是灵活应用分数的基本性质。

一、打破现成概念的壁垒

人们常说数学是一门严谨的学科，主要指推理逻辑的严谨。殊不知，数学也有另一面——灵活机动，数学的机动性渗透到各个学科，生活的方方面面，这种机动性给数学带来了顽强的生命力。乘法分配律在四年级课本中是这样记述的：两个数的和与一个数相乘，可以先把它们分别与第三个数相乘，再相加。课堂练习中，要求学生类推到（a-b）×c=a×c-b×c，如果学生已经学过负数，这样类推并无不妥，但仔细考证，四年级的学生还没学负数，这样类推毫无严密性可言。如果这样的推广都可以作数，那么对分子通分这样学生自我探究得出的结论，为什么又不能作数呢？

数学是全人类的数学，不是数学家、教育家的专属品，任何一个学习数学的人，不分职业、国度、种族和宗教信仰，都有研习数学的权利，更何况是数学教师。有人曾说过：“教师，尤其是数学教师，不能止步于书中既定的概念，也不能止步于教材上框定的概念。这些现成的概念只是一种‘演习弹，是用来练胆、练手的。学生通过学习这些概念，能够掌握一些概念学习的基本方式和流程，于是，结合学习概念的经验和心得，根据自己的观察思考总结出一些全新的概念，并尝试着描述这些概念。”这样的数学教育才是科学的。数学是不断发展变化的，正是一些数学研究者前赴后继、不遗余力地创造数学新概念，才推动了数学的繁盛与兴旺。

二、自创概念不是无本之木

教师自创的概念不是“无中生有”，不是“闭门造车”，而是在教学中结合学情，揭露事物本质，适时创造的，以培养学生的独创精神。在教学中，我们常常会根据概念的性质归纳出一些诗歌或口诀辅助理解和记忆。如画圆的步骤，可以这样归纳：一定，二定，三旋转。又如量角的方法可以浓缩为：点对点，边对边，刻度要看另一边。对于一些题目，如果课本提供的方法较为复杂，教师还需要结合学生的知识基础进行优化，找出简易解法。如苏教版教材第八册第9页有这样一道思考题：

用1、2、3、4、5这五个数字分别组成一个两位数和一个三位数。要使乘积最大，应该是哪两个数？要使乘积最小呢？换五个数字再试一试。

要使乘积最大，就应该尽量使两个乘数达到最大值，那么就得在它们各自的最高位上安排数字4和5，然后再来考虑三位数十位上的数字的安排，优选3或2。考虑到与两位数最高位的乘积对总乘积的影响，3×5>3×4，2×5>2×4，两位数的十位上应该是5，如此一来，三位数的百位上只能是4。考虑到三位数前两位与两位数最高位的乘积对总乘积的影响，43×5>42×5，三位数的十位上应是3。稍作调试，可以得出使乘积最大的两个数是431和52。而要使乘积最小，两个乘数最高位上应优先考虑选择数字1和2，三位数的十位上只能选择稍大的数字3或4。通过反复调试，也可以得出使乘积最小的两个数是245和13。这些答案需要学生反复调试和修正，多次计算才能得出，如果换了数字，又得重新调试，即使摸索出规律也很难记住。教师可以这样引导：“设5个数从小到大依次排列为A、B、C、D、E。积最大时，配置应该是DCA和EB;积最小时，配置应该是BDE和AC。”在学生尝试推出结果前，笔者透露可以用减法解答。

呈现三年级的一道题目：用16根长为1分米的竹条围一个长方形，有几种围法？

在比较中学生发现：当长方形周长一定时，长和宽越接近，所围成的长方形面积越大;反之，长和宽相差越大，二者的乘积越小，所围成的长方形面积越小。学生总结出：两数和一定，差越大积越小，差越小积越大。应用这一规律来探寻两数的最大积和最小积时就会事半功倍：确定三位数的前两位和两位数时，只要在数值大的四个数字中选择三个安排就位，就能让差最小，调试最后的个位数，就易如反掌。在探求最小积时，只要把三位数的前两位和两位数，从最小的四个数字中选三个安排妥当，最大差值就能确立，再调整最后的个位数。如53与42，52与43，53+42=52+43，52-43<53-42，因此，52×43>53×42。这时只要调试521與43、52与431的积，找到大的。又如13与24，14与23，两组数的和相等，13与24的差大一些，那么积就小一些。接着确定个位数，选择配置135与24或者13与245的积，找到小的。

在配置个位数时，学生还发现一个规律：最后的最大的数字5连在大数后面，积反而变小了。因此，只要确定了两个数的前两位分别是13与24，那么这两个数最终就为13与245。这样教学不但将解题方法简化，而且让学生意识到数学方法的灵动性。

三、自带规律要一查究竟

有一些题目本身就带有明显规律，课本虽未明言，但教师可以引导学生探究发现。如苏教版教材第八册第34页第6题：

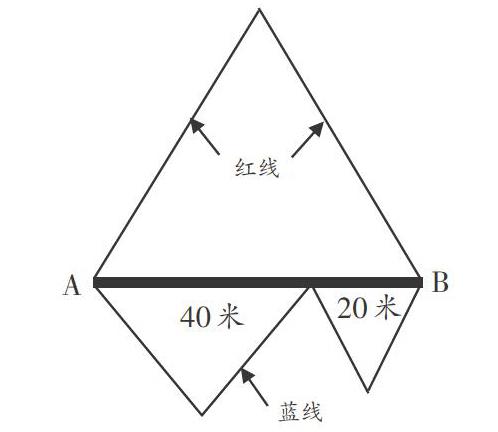
居民区有一块由三个大小不同的等边三角形组成的花园（如下图）。从A地到B地，走哪条路最近？图中哪两条路一样長？为什么？

教师参考用书中用计算来说明红、蓝两条路线长度相等：2个40加上2个20就等于2个60。在比较之后，笔者引导学生将两个红色三角形变为边长分别为10米、30米、20米的三个等边三角形，再与大等边三角形对比，学生归纳出：不管把蓝色三角形沿着一条边变为几个小等边三角形，像图中这样设计，大三角形周长始终等于若干个小三角形周长的总和。

又如苏教版教材第七册第101页第3题：

先用计算器算出下面各题的积，再找一找有什么规律。

142857×1=      142857×2=          142857×3=

142857×4=    142857×5=  142857×6=

习题的本意是先求积，再查探规律。在学生发现“马灯数”的奇趣后，笔者顺势追问：“142857从1乘到6存在这样的规律，那么乘7或7之后的数字还能有这种规律吗？”学生计算后发现，142857×7=999999，规律延续到数字7就中断了。学生充满了疑惑：“难不成这个规律与7犯冲吗？”笔者因势利导：“跟7到底有什么关系？可以一探究竟，用1～6这6个数字除以7试一试。”学生得出：

1÷7=0.142857142…

2÷7=0.285714285…

3÷7=0.428571428…

4÷7=0.571428571…

5÷7=0.714285714…

6÷7=0.857142857…

7÷7=1

原来商中的“142857”来头不小，竟然和1除以7的商有关联。虽然循环小数没有涉足，但借助计算器可以查明“142857”的原委。

欲速则不达。放慢节奏、扣住数学本质，才可以创造性教学、创新教法，与学生一道在题目中含英咀华，感受数学的神奇，在创造概念中，让学生获得探索数学的经验。

[ 参 考 文 献 ]

[1] 吴谦彪.运用动态教学策略，优化几何概念学习[J].数学教学通讯，2019（13）.

[2] 平国强.分析概念结构  促进有效建构[J].教学月刊小学版（数学），2012（04）.

[3] 林忠.让学生灵活建构数学概念[J].江苏教育，2007（18）.

（责编 吴美玲）