问题导学,让数学学习走向本质理解
2021-03-16葛敏辉
葛敏辉


[摘 要]“小数点搬家”的学习内容主要是探索小数点位置移动引起小数大小变化的规律,紧扣本质提出问题,通过问题导引学习,可以让学生真正理解规律背后的数学本质。通过问题导学,激活学生已有的知识和经验,层层深入地引领学生探索规律、深化理解,从而体会到十进位值制的优越性。
[关键词]理解;本质;问题;导学
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)05-0011-04
“小数点搬家”这一课在不同的教材里有不同的要求,有些教材单独给它安排了1课时,有些教材却没有。这一内容到底该不该教?如果教,要教给学生什么?怎样才能帮助学生理解这个规律背后的数学本质?这值得一线教师深入思考、探索和实践。
一、学前思考
(一)教之困——可以不教吗?
北京海淀区中关村第一小学的陈千举老师通过研究发现,不管有没有专门学习“小数点搬家”这一内容,学生在解答相关题目时并没有明显差异。那么,有的教材为什么要安排这一内容呢?
(二)学之惑——小数点会搬家吗?
在学习“小数点搬家”的过程中,经常有学生产生疑问:小数点一直在数的整数部分和小数部分的中间,并没有“搬家”,教材是不是错了?数学课堂应关注学生的真问题,以问导学,所以本节课就可以这个问题为核心,引领学生深入探究“小数点会搬家吗?到底是谁在搬家?为什么叫小数点搬家?”这样,有了真问题的课堂,学习才会真正发生。
(三)学情分析——理解水平如何?
为了了解学生对于“小数点搬家”的理解水平,笔者对四年级130名学生进行问卷调查。
【问题1】观察0.01、0.10、1.00这组数据,小数的大小发生了什么变化?
[ 特征描述 占比 水平0 错误描述 3.1% 水平1 笼统描述“从小到大” 14.6% 水平2 描述“相差关系” 3.8% 水平3 描述“倍比关系” 78.5% ]
通过分析数据发现,在学习“小数点搬家”之前,已经有78.5%的学生能描述数据之间的倍比关系。那么学生是否能解释这种变化?为此,笔者随机对40名学生进行了访谈,其中有24名学生可以借助十进制、位值制来解释这种变化,有3名学生能借助元角分来解释,二者占全部学生的67.5%。
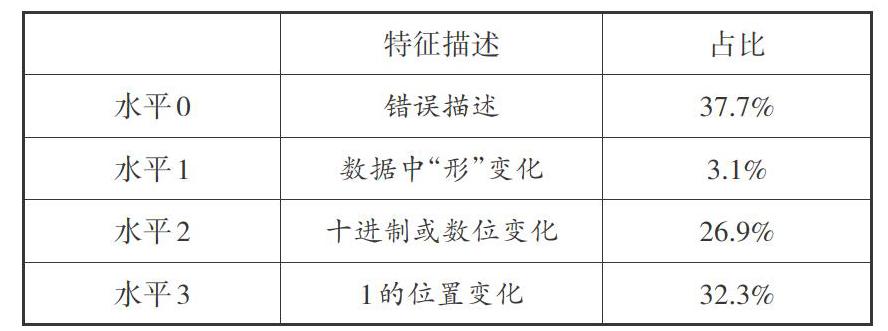
【问题2】你认为是谁的变化引起小数的大小发生变化?
[ 特征描述 占比 水平0 错误描述 37.7% 水平1 数据中“形”变化 3.1% 水平2 十进制或数位变化 26.9% 水平3 1的位置变化 32.3% ]
水平1的学生关注的是数据中形的变化,包括0的位置变化、0和1的位置交换以及“小数点的搬家”;水平2的学生能结合十进制、数位等已有知识关注到“十进制或者数字的数位发生变化,引发这组小数大小的变化”;水平3的学生能感受到“因为1所在的数位不同,所以位值不同引发了数据的变化”的本质。
基于以上情况,笔者有了以下的学习活动设计:学生已经可以借助数位顺序表、十进制、位值制等知识描述0.01、0.10、1.00的大小变化及关系,且思维已有一定的抽象水平,因此教材中大篇幅地借助元角分以及直观模型图来说明大小关系这个环节可以删去;可以问题引导学生通过迁移、自学、观察、比较、辨析等深度理解“小数点搬家”的本质,促进学生思维的生长。
二、学习活动
(一)任务驱动,唤醒学习经验
1.观察数字1在数位顺序表中的位置变化,初步感知数的大小变化
师:大家已经很熟悉数位顺序表了。数字1在个位安了一个家,你说这是几啊?(在数位顺序表的个位贴上“数字1”)
生1:1。
师:这個1很调皮,它想“搬家”了,它“搬到”了十位,这时候你会用哪个数来表示呢?
生2:10。
师:为什么要在1后面添1个0?
生3:因为没有0它就变成了1。
生4:要用0占位。
师:你发现了什么?
生4:数字1“搬家”后,改变了位置,数的大小也变了。
生5:1扩大了10倍,变成了10。
生6:乘10,1×10=10。
师:也就是,“1→10”得到的数是原数的10倍(也就是乘10)。
2.深入体验,发现数字移动位置的变化规律
师:现在数字1又“搬家”了(数字1移到百位),这时是什么数?
生7:100。
师:你们还发现了什么?
生8:1从十位移到百位,扩大了10倍。
生9:1在不同的数位上就会得到不同的数。
生10:数字“搬家”会引起数的大小发生变化。
师:如果1又“搬家”了,从百位“搬回”到十位,数又发生了什么变化?
生11:从百位到十位,100变成了10,相邻两个单位之间的进率是10,所以缩小了十倍。
师:你们说的缩小了十倍,除以10,也就是平均分成10份,取一份,也可以说得到的数是原数的十分之一。假如移到个位呢?
生12:从100到1,得到的数是原数的百分之一。
生13:从10到1,得到的数是原数的十分之一。
师:通过刚才的活动你有什么发现?
生14:数字1从个位移到十位,数扩大10倍;从个位移到百位,数扩大100倍。
生15:增大一位(指移到高位),得到的数是原数的10倍。如果倒退一位(指移到低位),得到的数是原数的十分之一。
生16:数字1往左“搬”一位,就扩大到原来的10倍,往左“搬”两位,就扩大到原来的100倍。
生17:数字1往左“搬”一位就乘10,往右“搬”一位就除以10。
师:说得真好!为什么变化规律是“移动一位就是10倍”?
生18:因为相邻两个计数单位之间的进率是10。
[思考:数位顺序表实现了自然数和小数的完美统一,以此为工具,引导学生观察1在数位顺序表整数部分中的位置变化,可以激活学生已有的知识经验,使学生感悟到“数字搬家”引起数的大小变化的规律和内涵,为学生自主构建规律搭好认知支架。]
(二)自主迁移,构建知识体系
师:是不是只有在整数部分移动位置才有这样的变化规律?请验证你的猜想,并在作业纸上写下来。
生1:小数部分也有这样的规律。1从十分位移到百分位,也就是0.1到0.01,得到的数是原数的十分之一。
生2:如果反过来,1从千分位移到百分位,也就是从0.001到0.01,得到的数是原数的10倍。从百分位移到十分位,也就是0.01到0.1,得到的数是原数的10倍。(如图2)
生3:我发现在小数部分和整数部分之间也存在这样的规律。1从十分位到个位,0.1乘10等于1,1从十分位到十位,0.1乘100等于10。(如图3)
……
师:能不能对你们发现的规律做个总结?
生4:不管是整数部分还是小数部分,只要数字往高位移动一位,得到的数是原数的10倍,往低位移动一位,得到的数是原数的十分之一。
师:是的,在整个数位顺序表上,“数字搬家”1位,都会有10倍的变化规律。为什么有这样的变化规律?
生5:因为相邻两个数位的进率都是10。
[思考:从“数的搬家”入手,通过整数部分的体验迁移到小数部分,学生自主借助数位顺序表,在探究、沟通、联系的学习中理解“数字搬家”引起数的大小变化规律,充分经历知识形成和关联的过程。]
(三)冲突融合,深化规律理解
1.自学反馈,认同课本中关于小数点“搬家”的规律介绍
师:课本是怎么介绍今天学的知识呢?请自学课本第35页。(学生自学)
生1:一個数的小数点向右移动一位,得到的数是原数的10倍;一个数的小数点向左移动一位,得到的数是原数的十分之一。
师:能不能结合例子说说?
生2:0.01的小数点向右移动一位变成0.1,所以得到的数扩大了10倍;0.1的小数点向左移动一位变成0.01,得到的数是原数的十分之一。
师:这样的规律在其他小数那里也存在吗?请举例验证。
生3:其他小数也存在这样的规律。
学生作品(如图4):
2. 引发冲突,让学生深度思辨变化中蕴含的实质
师:我们发现的是“数字搬家”有数的大小变化规律,可是课本上介绍的是“小数点搬家”有数的大小变化规律,到底是谁在“搬家”?
生4:我觉得是“小数点搬家”。
生5:我觉得是“数字搬家”。
师:你同意谁的意见?请说出理由。
生6:我同意“小数点搬家”。比如说8.88乘10等于88.8,小数点前面原来有一个8,扩大10倍后小数点前面有两个8,“小数点搬家”了。
生7:我同意“数字搬家”。因为小数点是隔开整数部分和小数部分的,不会“搬家”。
师:谁听懂了生6的意思?
生8:小数点一直在整数部分和小数部分的中间,怎么会“搬家”?
生9:我也认为小数点是不会“搬家”的,在数位顺序表上就看得很清楚(上台演示),它一直是整数部分和小数部分的分界。
师:生6,你觉得呢?
生6:表面上看是“小数点搬家”,其实是“数字搬家”。
师:为什么你改变了想法?
生6:因为小数点在数位顺序表中的位置是固定的,其他数字的位置都是可以移动的。
3.思辨交流,体会数学人为规定的合理性
师:是啊,表面上看是“小数点搬家”,但是实际上小数点是不会“搬家”的,其实是数字在“搬家”。那么明明是“数字搬家”,为什么教材却说是“小数点搬家”?
生6:“小数点搬家”可能更加方便一点。
师:怎么能让大家看出“小数点搬家”的方便?
生7:0.057×10=0.57,如果说“数字搬家”,5往高位移一位,从百分位移到十分位,7也往高位移一位,从千分位移到百分位。这样很麻烦!如果用“小数点搬家”,只要说“小数点往右移动了一位”就好了。
师:你们有什么感觉?
生8:这样的话既可以让语言变得简洁,也能说出想表达的意思。
生9:一个数如果数字很多,说“数字搬家”会很浪费时间,说“小数点搬家”就很方便。
师:是啊,确实是“数字搬家”,但是用“小数点搬家”来表达会显得更方便,因此人们就把这个规律叫“小数点搬家”。
4.练习(略)
[思考:你有什么收获?你有什么疑问?为什么明明是“数字搬家”,教材却说“小数点搬家”?三个问题的递进,让学生经历了“平衡—失衡—新的平衡”,第一问发展学生自学和梳理知识的能力,第二问发展学生自主辨析知识的能力,第三问让学生感悟数学发展的合理性,学生逐步走近知识本质,走向思维生长。]
三、学后反思
(一)紧扣本质提出问题,让导学有一个靶向
在思考并教学这一内容的过程中,笔者真切感受到,远离本质的提问和练习,难以让学生理解本质、举一反三。本文中的问题指大问题,大问题是指那些直指本质的、涵盖教学重难点的、具有高水平的、以探究为主的问题。“到底是谁在搬家?”显然是一个好问题,以此来引导学生深入开展学习,自然事半功倍。
(二)立足学生分析问题,让数学有一些温度
在课堂中不难发现,数学知识与学生理解常常是两张皮,数学变得生硬而难以理解,学生把主要精力花在模仿和操练上,数学似乎显得有些冰冷。事实上,学生已经知道了什么?疑惑在哪里?有哪些经验可以支撑他们思考?回归学生,暴露他们的困惑,让他们在需要和思考中找到获得感。这节课的知识对于学生来说,困惑点在“小数点怎么会搬家?”“明明是数字移动,为什么要说成小数点移动?”。学生在自我需求中分析问题、理解规律,从而体会到十进位值制的优越性。如此的活动充满思考,如此的数学富有温度!同时,学生在活动中学会了思考,释放了潜能,生成了智慧。
(三)自主建构解决问题,让课堂有一个旋律
聚焦本节课,自主性的学习设计、开放性的思辨场域、及时性的反思活动共同促成了学生的自主建构和思维爬坡。学生在与同伴对话、与教师对话、与教材对话、与自己对话的过程中不断质疑、反思、辨析,透过表象,结合数位顺序表认识到数学的本质,即小数点不会动,它是整数部分和小数部分的分界;它是数字的移动引发数的大小变化规律的关键点;人们为了表达方便称这规律为“小数点搬家”;规律变化的根源是十进制;等等。不难发现,课堂上始终是学生在自主活动、主动对话、积极思辨,解决问题的过程就是他们自主建构的过程。
总之,教师要把握数学学习的本质,利用好学生的认知冲突和思维活动,要善于“把握学情,顺学而导”,导在疑难时,导在关联处,要以问导学、以问促学,实现“不教之教”。
(责编 金 铃)
