挖掘隐藏基本图形 提升论证求解能力——从2019年广东省中考数学第24 题谈起

广东省东莞市可园中学(523000) 翟燕芳

对近年广东省中考数学试卷的分析中发现, 其中第24题均为平面几何压轴题, 且都以圆作为背景进行问题设置,需要考生具备良好的数学素养,由于题目中条件较多、图形较为复杂,考生往往无从下手、望而生畏.因此,在中考备考过程中,教会学生如何从复杂的图形中挖掘出隐藏的基本图形,化繁为简,逐渐提升学生的推理论证与运算求解能力,显得非常重要,下面笔者从2019年广东省中考数学第24 题谈起,不当之处,敬请批评指正.

1 试题回放

如图1,在∆ABC中,AB=AC,⊙O是∆ABC的外接圆,过点C作∠BCD= ∠ACB交⊙O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.

(1)求证:ED=EC;

(2)求证:AF是⊙O的切线;

(3)如图2,若点G是∆ACD的内心,BC·BE=25,求BG的长.

图1

图2

2 试题分析

本题以圆和等腰三角形为背景命制,设计常规,清晰又略带小惊喜,主要考查圆的基本性质、圆周角定理、等腰三角形的判定及性质、线段垂直平分线的性质、平行四边形的判定、切线的判定、三角形的内心的概念、相似三角形的判定及性质.

(1) 要证明ED=EC, 如图3, 首先考虑证明∠EDC= ∠ECD, 由题已知AB=AC得∠ABC= ∠ACB,再由基本图形“角—弧—角”模式(下文3.4 介绍),∠ABC −−∠ADC得∠ABC= ∠EDC,由已知∠BCD= ∠ACB,则∠EDC=∠ECD推出ED=EC.

图3

图4

(2)连接OA,要证AF是⊙O的切线, 如图4, 则只需证明∠OAF=90°, 但条件中并无提供直角的条件, 观察图4 可证OA⊥BC, 再证BC//AF即可.由半径组成的基本图形, 连接OB、OC,则AB=AC,OB=OC利用线段垂直平分线的性质得OA⊥BC.由(1)得∠ABC= ∠ECD,则AB//CF,由已知条件得AB=CF,从而得到四边形ABCF为平行四边形,问题得证.

(3) 由BC · BE= 25 引 导 学 生猜想与BC,BE有关的相似三角形,即考虑∆BAE与∆BCA相似, 分拆出基本图形属A 型, 如图5, 只需证∠BAE= ∠BCA由“角—弧—角”模式,得∠BAD=∠BCD.

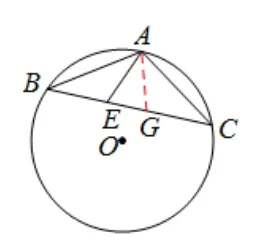
图5

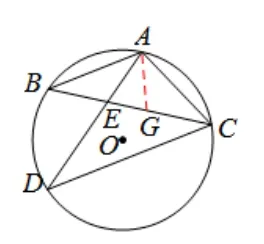
图6

如图6, 由题已知∠BCD=∠ACB, 则∠BAE= ∠BCA, 那 么∆BAE～∆BCA, 所以推 出AB2=BC · BE, 得AB= 5.题目需要求BG, 本题小惊喜为G是内心, 应引导学生连接AG, 观察图5 猜想∆BAG是等腰三角形, 由图6 得∠BAG= ∠BAD+∠DAG, ∠BGA=∠GAC+∠ACB, 因为点G为内心, 则∠DAG= ∠GAC,从而得∠BAG=∠BGA,推出BG=AB=5.

3 追根索源

上述分析不难发现,每个问题解决的关键点都源自某个基本图形,圆是以一个定点,以一条定长旋转一周所形成封闭的平面图形.圆心、半径、直径、弧都是圆的基本元素,掌握这些基本元素构成的基本图形,培养学生的图感,对解决复杂的综合题有着重要作用.

3.1 与圆心有关的基本图形

由于圆心是圆的对称中心,是任何一条直径的中点.若题目条件中出现或能证明另一个中点, 如图7 的点D, 常把这个中点与圆心连接成三角形中位线,进行有关推理得平行,进而推出边、角之间数量关系,这个基本图形简称“中位线模型”.

图7

如2018年广东省第28 题,如图8,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C, 连接AC、OD交于点E.(1)证明:OD//BC;

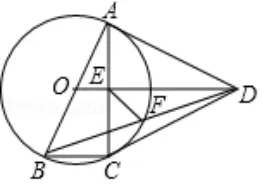
图8

方法1: 应证∠AEO=∠ACB,∠ACB为直径AB所对圆周角为90°,如图9 只需证明∠AEO= 90°,由题AD=CD,根据“三线合一”需提供“一线”,然而在∆ADE与∆CDE中无法直接证明.

图9

因此引导学生添加辅助线OC如图10, 使得能构成基本图形之一“筝形”, 由半径OA=OC,AD=CD,得OD是AC的垂直平分线, 从而得∠AEO=∠ACB=90°,问题得证.

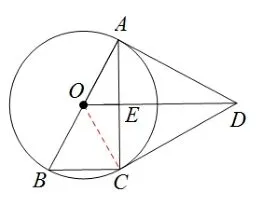
图10

方法2: 由方法1 得OD是AC的垂直平分线,即E是AC的中点,利用“中位线模型”问题得证.

3.2 与半径有关的基本图形

在同圆中,所有的半径都相等,利用这一特性,任意不在同一直线上的两条半径均可构成等腰三角形,常利用半径组成的“等腰”证“等角”.等腰三角形,角平分线,平行这三个条件中已知任意两个即可推出第三个结论,可以把个模型称为“铁三角”,如图11 和图12,“铁三角”在圆的背景下,两半径提供了“隐藏”等腰三角形,这是常见解题的突破口.

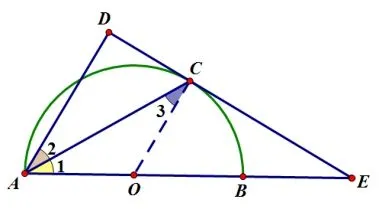
图11

图12

如2017年广东省第24 题,如图13,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(2)求证:CF=CE;

需要证CF=CE,分拆出相关图形如图14,图感的直觉此处需要连接AC,即可把CF,CE分拆到两个直角三角形中,证全等即可(此方法略);或证明AC为∠FAE的平分线,要证明角平分线,圆中时刻“隐藏”等腰三角形,即利用“铁三角”模型如图15, 只需证明OC//AF, 由题中CF⊥AF,CF为切线易得OC//AF.

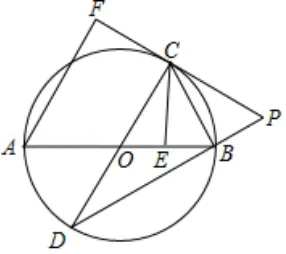
图13

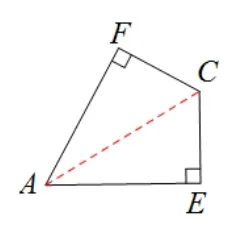
图14

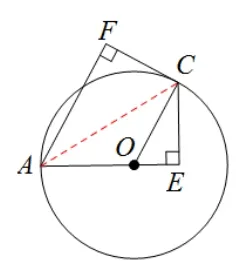
图15

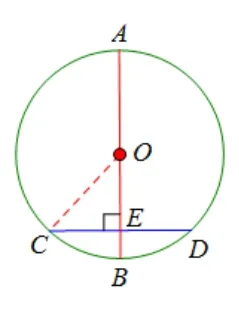
图16

3.3 与直径有关的基本图形

在同圆中,所有的直径都相等.其中与直径有关的“垂径定理”和“直径所对的圆周角是直角”这两个定理尤为重要.当观察直径具备垂直于弦的条件, 常会构建如图16 所示的Rt∆OEC,利用勾股定理进行计算推理,或提供两边相等如图16 中的CE=DE得AB⊥CD.

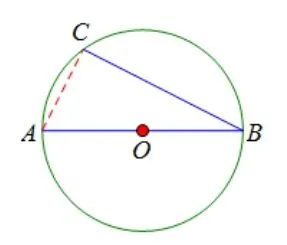
图17

另外直径常可联想直角,必要时需添加辅助线构成由直径所形成的直角三形这个基本图形,如图17.其中2017年广东第24(2)题,2018 广东第24(3)题均需添加辅助线构成直径所对的圆周角是直角这个基本图形来解题.

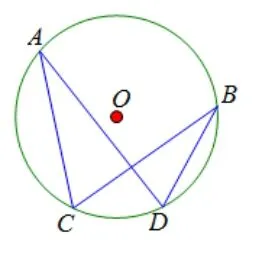
图18

3.4 与弧有关的基本图形

在圆中,弧是其他几何图形没有的元素.同弧或等弧所对圆周角相等,都等于所对圆心角的一半,也就是说,同弧或等弧可以推出有关角的等量关系,不妨称为“角—弧—角”模式,如图18 中的圆周角∠A所对的弧为又对着另一个圆周角∠B,则可推∠A= ∠B.这是圆中特有的证明角相等的重要方式.如2019年广东省第24 题的第(1)(3)题均利用“角—弧—角”模式有效解题.

3.5 与相似有关的基本图形

圆的综合大题之所以复杂, 原因在于圆本身元素丰富,而且它的包容性大,与强大的三角形,四边形等均能完美结合.从2017年—2019年的广东数学中考题分析,圆与相似三角形结合度最高,在近三年广东中考题第24(3)题的解答过中均需找到相似的基本图形,如2017年分拆出子母型,2018年、2019年都需分拆出相似A 型.如能熟练从复杂图形中分拆出相似的基本图形,解题的成功概率大大提高,下面总结出常见相似基本图形分别有A 型、X 型、子母型以及“一线三等角”的K 型,如图19.

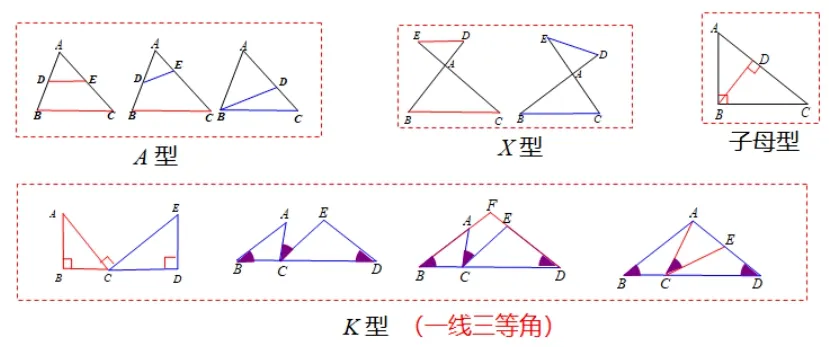
图19

4 解后反思

复杂的图形都来源于几个基本图形结合而成,如果学生能从中追根索源,抽丝剥茧,分拆出基本图形,问题就能迎刃而解,但分拆图形能力不是与生俱来具备,需要教师在平时教学中不断引导,培养的,下面谈谈做法.

4.1 重视基本概念与定理的讲解

教师在讲授一个新的概念、定理时,忌只讲结果,求套用.要讲清新公式、定理使用条件,分析其推导过程,让学生能知其来龙去脉,并能把文字定理,转化成数学语言表达.让学生感受定理中的图形,图形中的定理,初步形成基本图形.

4.2 重视总结基本条件,基本图形互推应用

在讲授整章内容后,要求学生利用思维导图分类总结公式、定理的应用条件,作用等.如在圆这章中总结与角有关的定理有“垂径定理”、“弧、弦、圆心角、圆周角的关系定理”常用“角—弧—角”模型、“直径所对的圆周角是直角”、“圆内接四边形对角互补”、“切线性质定理”、“切线长定理”等.特别注意在图形中标注定理的使用条件与结论,产生出基本图形.学生能看着基本条件联想到基本图形,或者观察出基本图形,能从条件中找出基本条件进行有效解答,真正做到心中有图,以不变应万变.

4.3 重视体验分拆基本图形的过程

在讲解综合大题时,教师注意示范分拆基本图形的步骤,要让学生充分体验分拆过程.常利用一题多解的训练,累积基本活动经验,深入了解基本图形的特征与性质,逐步学会从复杂图形中分拆出“隐形”基本图形或添加辅助线补成基本图形;由辨识基本图形到变换基本图形,从而打开解题突破口.

在平时教学中以基本图形为抓手,通过“感图—识图—用图—变图”四个过程,让学生在获得基础知识的同时,增强几何直观能力;在锻炼分拆基本图形的基本技能的同时,增强逻辑推理能力;在应用基本图形的同时,培养了图感,积累基本活动经验,有效解题,体验获得成功的乐趣,增强了学习数学的自信,真正提升了学生论证求解的能力,培养学生的数学核心素养.