思题所解 叙己所思——2020年广东中考数学压轴题的深入研究

广东省肇庆市宣卿中学(526000) 孔德泉

2020年全国各省市中考陆续落下帷幕,中考试题凝聚了命题专家的集体智慧,具有权威性、示范性、借鉴性,研究中考压轴试题对数学深度教学大有裨益.笔者对广东中考压轴题进行研读挖掘,体会深刻,撰写成文,以此与读者分享.

1 中考真题 情境再现

题目: 如图y=+bx+c与x轴交于两点,点A,B分别位于原点的左右两侧,BO= 3AO= 3, 过点B的直线与y轴正半轴和抛物线的交点分别为C,D,

(2)求直线BD的函数解析式.

(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上,当∆ABD与∆BPQ相似时,请直接写出所有满足条件的点Q的坐标.

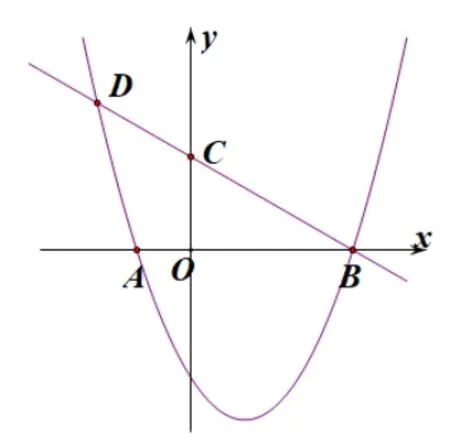
图1

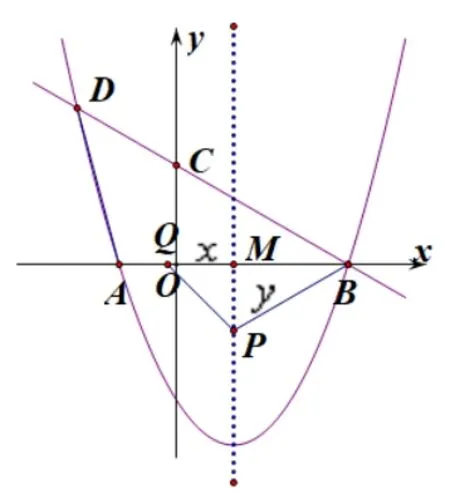
图2-1

2 解法研究 思路优化

思路一: ∆ABD三条边的长均可求出,用三条对应边分别成比例进行求解,此解法运算量十分繁琐.

情形1(图2-1): ∆ABD～∆PBQ,设QM=x(x >0),MP=y.平方化简得,得4 +y2=,x2+y2=两式相减得解得x1=,x2=−2(舍去),此时点Q1(1−

其他情形同理可得:

图2-2

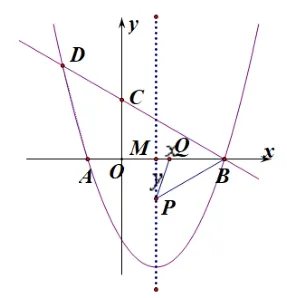
图2-3

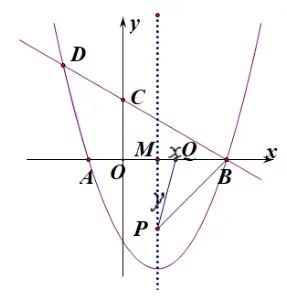
图2-4

思路二: 若发现∠ABD= 30°, 则PM=对于上述前两种情形只需设一个未知数, 利用两条对应边分别成比例,解一元方程,减少了运算量,达到思路一的优化目的.

船舶设备在安装中由于组件安装的体积较大，重量较大，因此在安装中通常借助起吊机，手工辅助机械装置，进行相关组件设备的安装。在此过程中分析大型组件设备安装中的减振措施，对于设备安装中的准确性提升意义重大。具体分析在实际发展中设备安装准确性的保障，对于设备后期的应用质量保障，以及设备的实际应用效果提升奠定了良好的基础。其中具体分析船舶设备安装的准确性，主要体现在船舶设备安装位置，安装高度，安装水平度的准确性，确保其设备组件后期在运行中的稳定性和合格性。

思路三: 若发现∠ABD= 30°且∠ADB= 45°,利用三角函数确定边长之间的关系,求解该题目将更加简便,而∠ADB=45°极为隐晦,需学生具有丰富的数学经验和敏锐的直觉思维,需要验证AC⊥CD,AC=CD,需要全面理解题目中三角形的边角元素构成特点.

章建跃博士:“数学是玩概念的,让学生养成从基本概念出发思考问题和解决问题的习惯”.以上几种思路正是沿着相似三角形的对应角相等, 对应边成比例的定义进行探索,不同的求解层次展现出学生不同的思维水平,具有良好的区分度.在有效的时间内快速地解题,“先动脑后动手”将变得相当重要, 学生也会在解题过程中进行不同层次间的转化,在求解题目中不断调整并寻求其他方法,学生不同的能力水平会呈现不同的表现,这恰好是压轴题的使命所在,正是题目设置的最突出的亮点—有效考查不同学生的数学能力.

3 几何探路 本质解释

该题目是抛物线背景下的几何问题,去除抛物线的“外衣”,研究其几何本质属性,又可得到新方法.

思路四: 情形1, 2(如图3-1.2) 作点D关于AB的对称点D′, 连接AD′,D′B, 对称轴与D′B相交于点P, 作PQ1//AB交AB于Q1,得∆ABD′～∆Q1BP,可以得到射线BA上一点Q2,使BP2=BQ1·BQ2,得

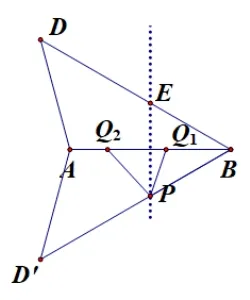
图3-1.2

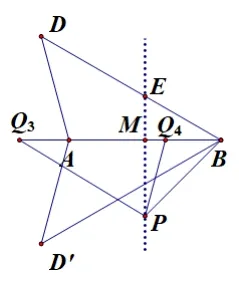
图3-3.4

情形3,4(如图3-3.4)同理作点D关于AB的对称点D′,对称轴上找一点P,作∠MBP= ∠D(实际作45°),过点P分别作PQ3//BD,PQ4//AD′,分别交AB于点Q3,Q4,由得Q3;再由BP2=BQ3·BQ4得Q4.

4 考查分析 题目欣赏

这是一道典型的综合性极强的题目: 考查一次函数与二次函数的解析式,图形变化,图形与坐标,两个点的动态变化,寻求三角形相似关系中对应角的不变性,对应边成比例的稳定性,要求学生具备猜想,分析,推理,分类,综合,类比等多种思考方法,对学生的几何直观,运算能力,推理能力均有较高要求,体现数学的应用意识和创新意识,考查数形结合,分类讨论,转化等数学思想方法的综合运用.

∆ABD是两个内角分别为30°, 45°特殊角的三角形,这样的三角形非常典型, 而函数的二次项系数为什么是无理数在不改变题意的前提下, 点C在y轴上,BO= 3AO,∆ABC为直角三角形,这其中的内在联系是怎样组织的? 系数能否调整为有理数,使之更加简洁,因此笔者做如下尝试:

设A(−m,0),B(3m,0),抛物线:y=a(x+m)(x−3m).代入得am=研究到这里,我们发现抛物线与x轴左交点的横坐标和二次项系数之积为定值,取AO=1 时,二次函数系数恰是本题目中的无理数若调整函数的二次项系数使其美观,不妨取a=1,则抛物线与x轴交点的坐标数据变得错综复杂, 不利于发现∆ABD中如30°,45°这样的特殊角,既然题目这样设置,我们猜想这应该是命题组的设计意图,我们试图做其他的改动将失去题目本身的考查意义.由此可见,原题目竟是何等的美丽与和谐.

5 题目变式 举一反三

对于任何一个优秀的题目,一线教师定会与学生们分享,如何讲解该题目,如何最大发挥题目的价值,为了追求最大功效,可尝试以下习题的变式进行过渡教学或者作为学生探究的素材.

题目变式1: (如图4-1)y=+bx+c与x轴交于两点,点A,B分别位于原点的左右两侧,过点B的直线与y轴正半轴的交点D恰好在抛物线上,满足BD=2.

考查问题不变: 第三问仍旧是“点P在抛物线……请直接写出所有满足条件的点Q的坐标.”

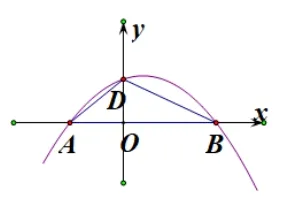
图4-1

图4-2

题目变式3: 已知条件均不变,所求问题中,可改变点P的位置,如点P在抛物线的对称轴上(去掉在x轴下方的限制要求);“点Q在射线BA上”改为“点Q在直线BA上”,利用这样的变式可进行更加深入的探讨.

6 求知若渴 学无止境

波利亚曾说:“解题从未存在完全彻底解决掉的题目,解完之后回头再看看,就是解题回顾;解题就象采蘑菇,当你找到第一朵后,在周围看看,因为他们总是成堆生长的”.2020中考压轴题是否有其他解法或者新的发现,期待读者的不吝赐教.