海洋钢桩清刷机器人清除粘附藤壶的力学研究

2021-03-19王立权李超陈凯云王刚庞乂铭

哈尔滨工程大学学报 2021年2期

王立权，李超，陈凯云，王刚，庞乂铭

(1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨 150001；2.黑龙江科技大学机械工程学院，黑龙江哈尔滨 150001；3.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001)

近年来，为了开采海洋资源，海上基础设施大量兴建，其中海洋钢桩因所处的环境复杂而受到海中的污损生物的附着[1]，导致每年投入巨大经济成本清除污损生物[2]。清理钢桩上附着的污损生物已经成为广泛关注且具有实际意义的问题。研究实践表明，海洋工程设施在不同海洋环境区带的腐蚀规律是不同的，其保护技术也相应不同。海洋中的区域大体分为5个区，依次是大气区、飞溅区、潮差区、全浸区和海泥区，由于浪花飞溅区[3]所处的特殊位置，这一区域的钢结构受到多种因素影响，例如：阳光照射、浪花冲击等，浪花飞溅区是腐蚀最为严重的区域带，腐蚀速度约是其他腐蚀区域带的3～10倍。目前，浪花飞溅区钢桩防腐蚀技术成熟[4]，但需要定期对钢桩进行人工清理维护。而人工清理维护费时、费力、成本较高、作业窗口时间短、作业难度大且还受季节影响。因此，实现海洋钢桩清刷作业的自动化,即用机器人来替代人工操作,将会大大节约劳动力,降低潜水员的劳动强度,提高清刷效率。目前，国外已开展了水下清刷设备的研究,但有的还是需要潜水员下水操作，为了提高海洋钢桩清刷的效率、节约能源,很有必要进行海洋钢桩清刷机器人的研究。

Iasgroup公司[5-6]是一家位于澳大利亚的综合性服务公司。针对海洋工程平台导管架高压水射流清洗工作，公司主要提供有2款产品Splash Genius和Splash Genius II，2款产品均可实现全自动清刷作业，有较大的导管架适应范围。Splash Genius是一款针对海洋工程平台导管架高压水射流清洗工作的产品，采用夹持攀爬技术，使设备夹持在导管架上，搭载高压水射流技术，清洗导管架上的污损生物及其他污垢。Splash Genius II是第2代全自动远程操作清理装置，用于在海底的管道，立管，导体，沉箱和桩上进行清洁和表面处理。

国内对这个领域研究的比较晚，20世纪80年代才开始发展水下的机器人。目前，我国很多机构对该领域做了较深入的研究。这几年，通过不断加大投入，将传统船体清洗工具和遥控技术机器人相结合，中国的研发工作取得较大的进展。典型的是中海油能源发展股份有限公司和浙江大学研制的机器人[7]，采用永磁吸附模块，空化射流清刷方式，具有导管自适应、视觉导航控制等特点，能够在水面以下100 m内进行污损生物自动化清理。但以上针对钢桩清刷的机器人都采用的是高压水射流技术，清刷效果并不明显。王立权等[8]提出将刮削法应用到清除海洋污损生物的过程中，使用工具成本低廉，清理效果较为理想。本文在前期研究基础上提出了一种海洋钢桩清刷机器人的三维模型方案，将刮削工具搭载在清理机器人上，从污损生物粘附根部进行清理，这种方法清理彻底且不污染海洋环境。本文以污损生物中的藤壶作为代表，通过建立藤壶三维模型，并对清除过程进行受力分析，建立藤壶粘附力、刀具的前角和水平切削力的数学模型，分析刀具前角、刀具位移、粘附力和切削力的关系，从而得出合理刀具前角及剪切力，为今后研究制造海洋钢桩清刷机器人提供有价值的参考。

1 清刷机器人与藤壶模型建立

1.1 清刷机器人模型建立

本文设计一款海洋钢桩清刷机器人模型方案如图1，上下2层圆环支撑平面和伸缩液压缸为机器人的整体支撑平面，主要可承载机器人各个装置；圆环支撑平面采用半圆式开合锁紧机构，用以将机器人开合并安装到圆柱钢桩上，可以环抱在海洋钢桩表面，固定后在圆环开合处进行锁紧，防止工作过程中机器人开合；上下圆环支撑平面中间连接伸缩液压缸，实现机器人整体上下移动；在上下圆环支撑平面上端搭载夹持装置，当机器人环抱在钢桩上之后，2组夹持装置开始工作，夹紧钢桩，将机器人固定在钢桩表面；在上圆环支撑平面下端，搭载一组齿轮齿圈和若干从动轮，马达驱动主动齿轮从而带动齿圈实现周向旋转；通过2组夹持装置合伸缩液压缸交替配合实现机器人在圆柱钢桩上的攀爬运动；并在机器人内部搭载正交式刮削清理刀具，以缩小机器人整体高度空间，将正交刮削法应用到清理污损生物中，以实对海洋圆柱钢桩的清理目的。

图1 海洋钢桩清刷机器人模型方案Fig.1 3D model plan of marine steel pile cleaning robot

1.2 藤壶模型建立

在海洋钢桩表面附着污损生物中，含有大量贝壳类污损生物较难清理，例如贻贝、藤壶等。其中属藤壶外壳坚硬，粘附力强，难清理，本文以藤壶为例展开研究。这些藤壶的钙质外壳能够稳定的附着在基底上的关键因素就是它们自身在底部分泌的藤壶胶，藤壶胶将2种不同的材料永久的粘附在了一起，附着在基底上的藤壶的横截面[9]，如图2所示。藤壶胶的粘性大且不易溶于水，一旦附着成年藤壶便永远不会移动或自我分离。图中以便强调藤壶胶的作用所以绘制的稍厚。

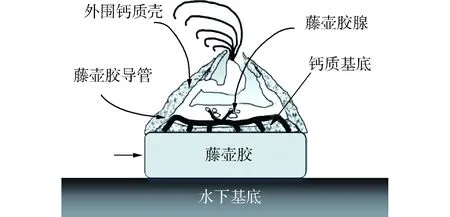
图2 附着基底的藤壶截面Fig.2 The cross-section of a barnacle on a foreign substrate

本文中建立藤壶附着模型，如图3所示，用梯形圆台代表藤壶的钙质外壳，夸张的增加了中间层的厚度来代表藤壶胶的粘弹性模型，让其附着在刚性基底上，形成藤壶附着的三维实体模型。

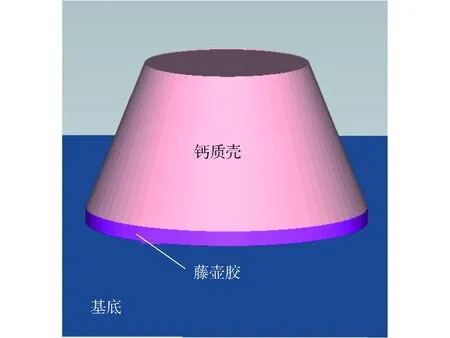
图3 藤壶的三维模型Fig.3 3D model of barnacle

几何模型的底部直径为d1，生长12个月的藤壶平均高度h1=5d1/12，顶部直径d2=7d1/12，藤壶胶厚度近似为h2=d1/24，如图4所示。

不同种类的藤壶，它们的生长直径范围8～43 mm不等[10]。本文中模拟清理样本为1 a生左右，直径约为24 mm的藤壶。

2 切削过程及理论与分析

2.1 切削过程

海洋污损生物藤壶通过自身分泌的藤壶胶附着在刚性基底上，因为藤壶胶上面生长着坚硬的钙质外壳且随着附着时间的推移变得越来越牢固，难以清除。本文中采用经典的刮削法清除方法，结合切削原理中正交切削方法及Pesika等[11]提出的剥离区方法，对其进行理论分析。刀具前角γ0的设置与切削原理中相同，即为刀具前刀面与被清理表面水平方向法线的夹角。清除藤壶过程中，藤壶会翘起形成如图5所示的过程。

图4 藤壶的几何模型Fig.4 Barnacle geometrical model and dimensions

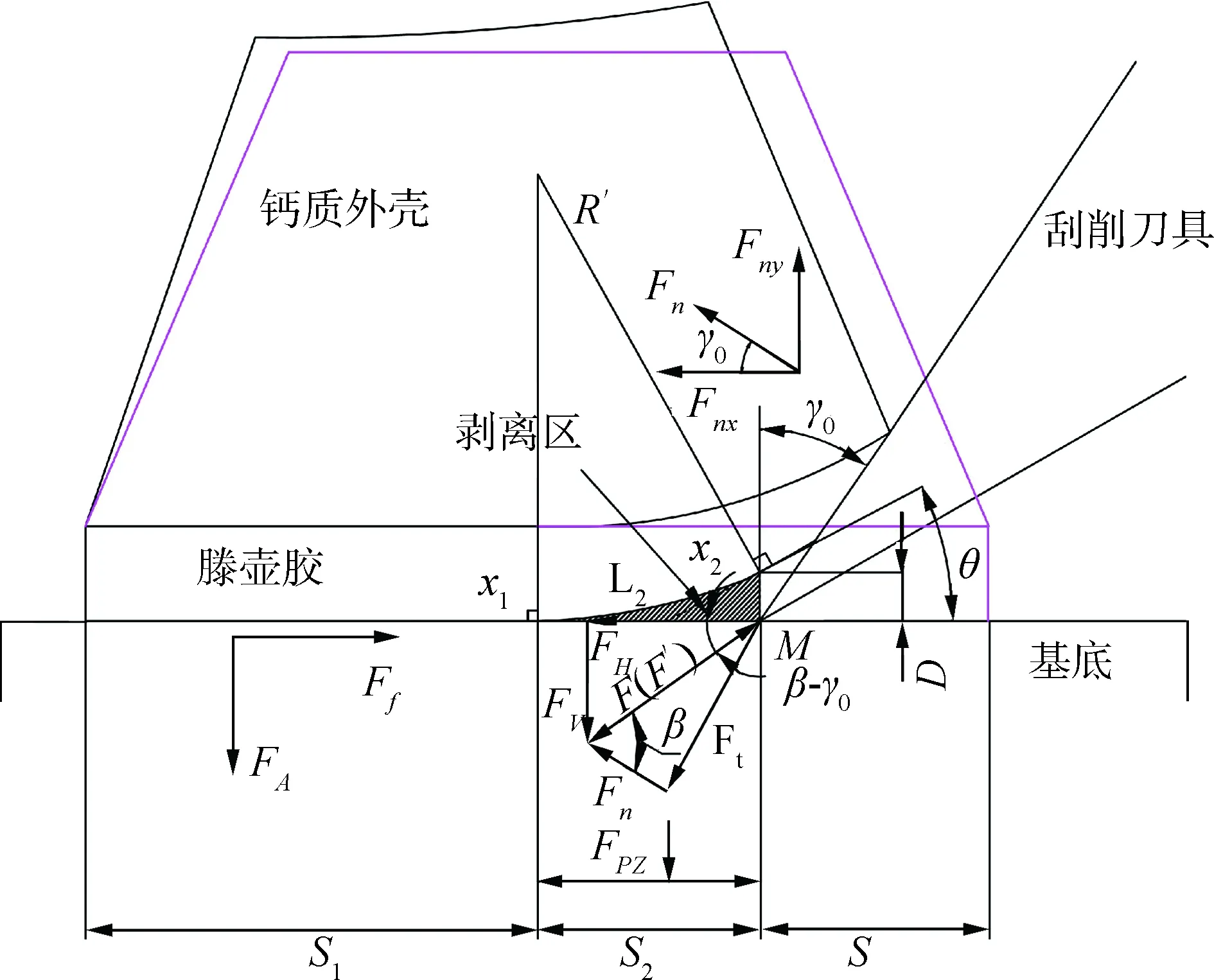
图5 清除藤壶受力分析Fig.5 Detailed analysis of removing barnacles

刮削粘附基底的藤壶与壁虎铲状垫的撕脱有相似处，同为粘弹性材料粘附在基底上，又不同于壁虎铲状垫撕脱，不同点在刮削清理藤壶时，藤壶外层有坚硬的钙质壳制约藤壶胶的大变形，与刀具接触的藤壶外壳发生形变，被翘起，即将脱离基底部分会形成类似于铲状垫的剥离区，剥离区是本模型中藤壶胶从基底被剥离开时且还留有粘附纤维的区域，即图5中x1、x2与刀尖点M3点围成的区域，对应水平距离S2；大于x2的竖直临界距离D的部分，粘附力已经失效，可以忽略不计。粘附在基底的部分按藤壶的粘附机理来分析计算，剥离区的粘附力用Pesika等的剥离区模型方法进行分析计算。

刀具刮削藤壶的过程中本文引用正交切削理论，假设刀具切削刃绝对锋利，后刀面与基底没有接触且不考虑后刀面的摩擦[12-13]。作用在藤壶钙质壳上的力有：前刀面的法向力Fn和沿着刀面方向的摩擦力Ft，F为这2个力的合力，此时有F′与F为大小相等，方向相反，保持平衡。反作用力F′可以分解成负责整个切削过程中主要工作的水平切削力FH和竖直方向上的FV；钙质外壳因前刀面的法向力Fn发生变形，Fn又可分解为垂直向上的力Fny和水平力Fnx；根据简单的三角函数关系可以得出：

(1)

式中：β是F与Fn的夹角，又叫摩擦角(tanβ=μ1)；γ0是刀具的前角。

2.2 剥离区的粘附力计算

为了方便理解，本文设计了藤壶底面的投影图，如图6，假设藤壶附着面积为半径为R的规则圆形，设AZ阴影面积为藤壶对应S1长度的垂直方向上的粘附力FA，PZ阴影面积为剥离区对应S2长度的粘附力FPZ。FA与FPZ的大小都与附着面积有关,可以分别计算各个区域所受的粘附力FA和FPZ。

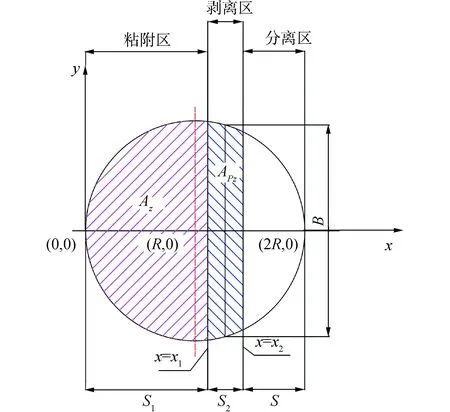
图6 藤壶底部投影Fig.6 Projection picture of barnacle bottom

(2)

式中：A是哈梅克常数；D是临界距离。

2.3 藤壶粘附力的计算

由图可知圆的方程为:(X-R)2-Y2=R2,由积分可知附着面积AZ：

(3)

取藤壶半径R=0.012 m为例，可得出AZ:

(4)

成年藤壶的粘附强度为P=9.252×105N/m2[9, 15]，假设清理的藤壶粘附时间都在1 a时间以上且都为成年藤壶，所以可得出剩余附着的粘附力FA：

(5)

根据竖直方向力的平衡关系，可知：

Fny=FA+FPZ

(6)

可得:

(7)

得到对应的粘附力曲线如图7。

可推导出FH的表达式为：

(8)

方程式中：A=0.4×10-19，R=0.012 m，剥离区实验得到最大摩擦力对应的θ=10°[14]，假设藤壶胶与基底和与前刀面的摩擦系数为0.25[11]，β=14°。

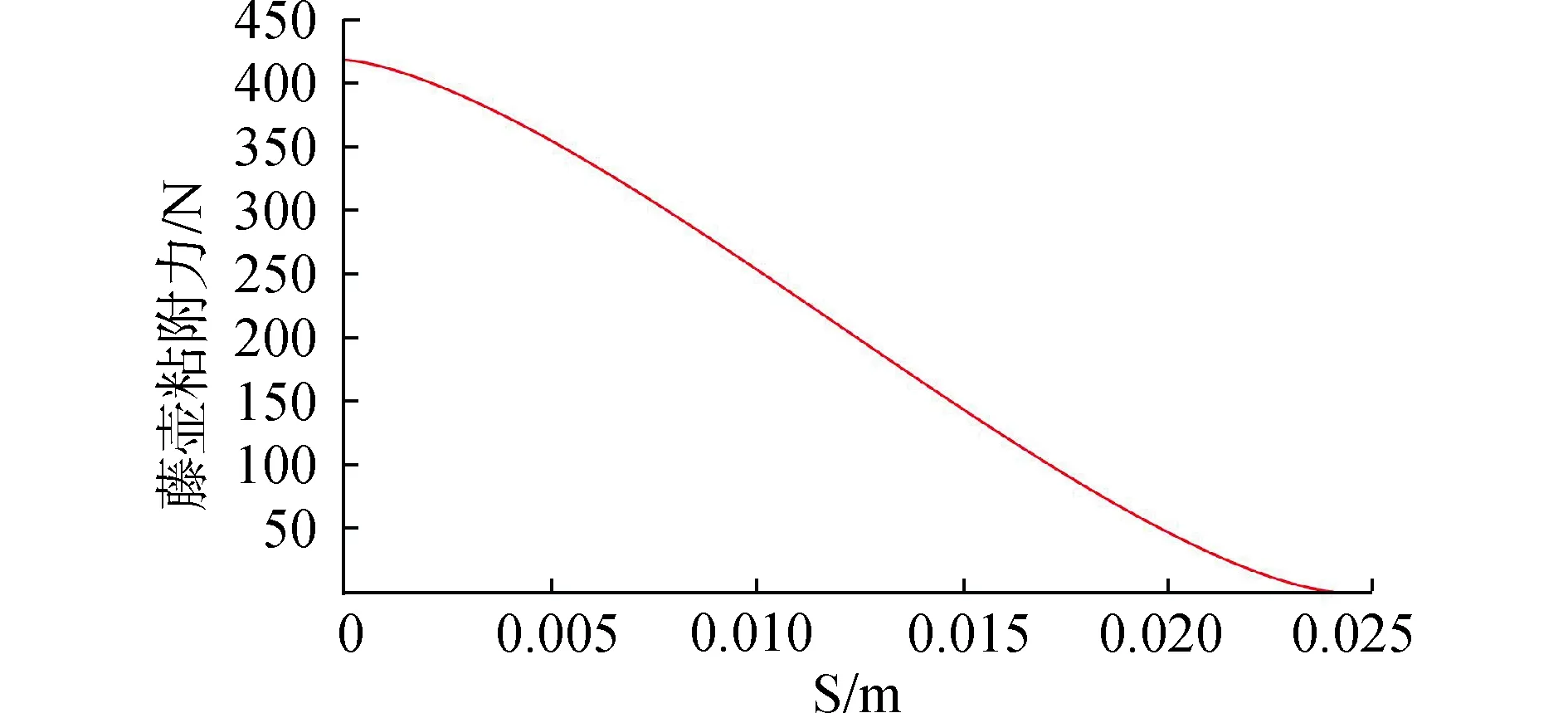
图7 藤壶底部粘附力曲线Fig.7 Adhesion force curve of barnacle bottom

通过方程(8)，可以得到刀具前角10°～90°对水平切削力FH的关系，如图8所示。

刀具前角对水平切削力FH的作用关系也可以画成3D图，如图9。刀具前角对水平切削力有较大的影响。前角在(0°，45°)内，前角越小，所需要的切削力越大；在[45°，90°)内，这个变化趋势相对变缓。考虑切削力和刀具的强度或使用寿命周期，来选择刀具的前角，刀具的前角的范围建议使用中间区域的角度，例如[30°，60°]。

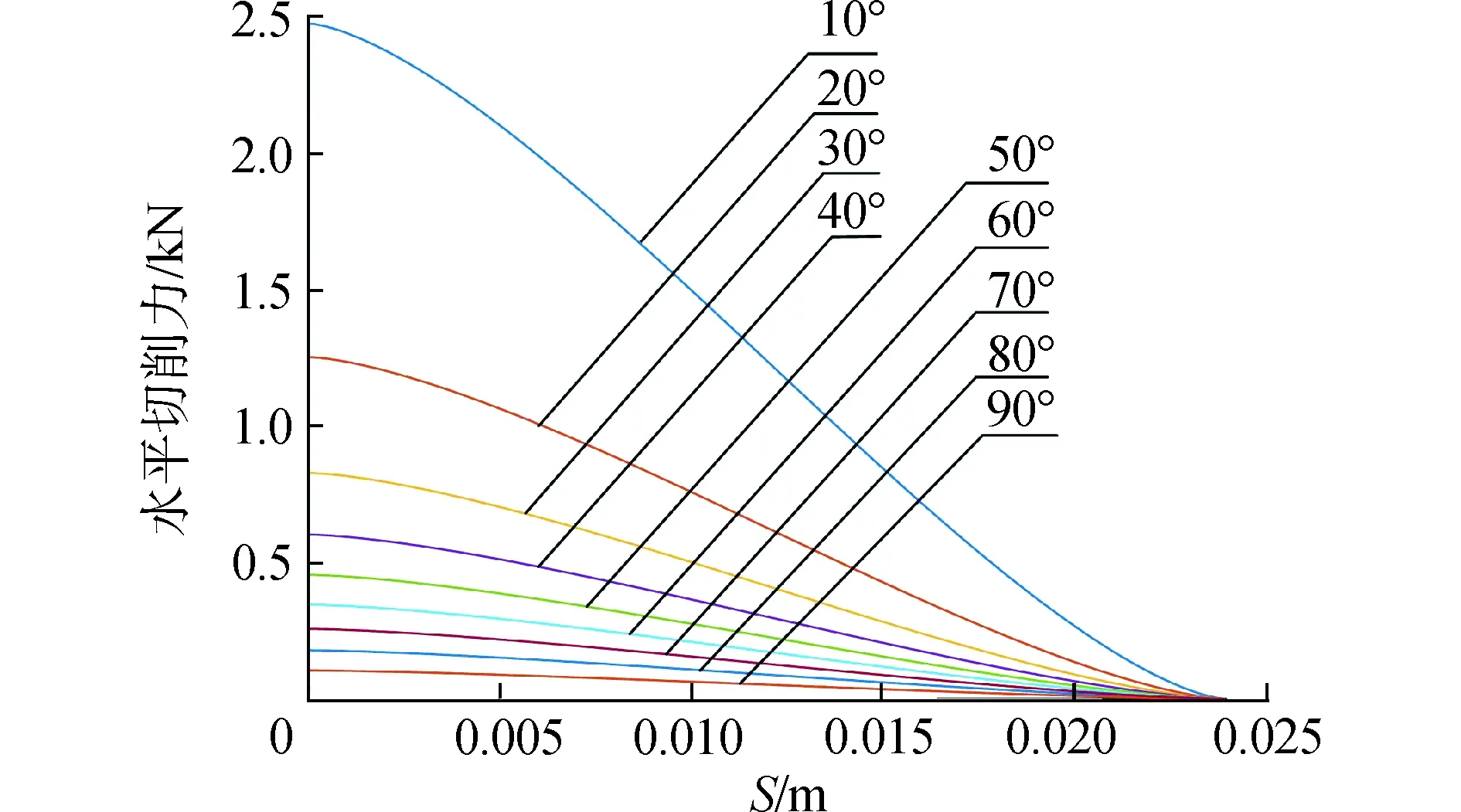
图8 不同刀具前角对应的水平切削力FHFig.8 The different blade rake angles correspond to the cutting force FH

同理可得FV：

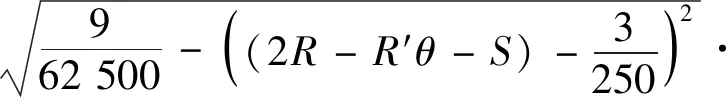
(9)

以前角为45°来计算切削力FH和FV的曲线如图10，FH和FV的值随着刀具的位移S的增大而减小，直到当S=0.024时，刀具的切削力变为0，同时藤壶完全被清除。竖直方向上的粘附力Fny=419 N，最大的水平切削力FH=523 N。

图10 刀具前角45°对应切削力FH和FV的曲线Fig.10 The 45° rake of blade correspond to the cutting force FH and FV

3 有限元仿真模型验证

为了验证分析模型，用有限元软件Hypermesh中的Ls-dyna建立有限元模型，如图11。藤壶直径d1为0.024 m，高度、藤壶胶厚度和顶部直径参见图4，刀具前角为45°，刀具速度为0.7 m/s。

在仿真中，如图11所示，设置刀具、藤壶外壳、藤壶胶为实体单元，设置刚性基底为壳单元以便于结果收敛。刀具与基底选用弹性材料，密度ρ=7.93×103kg/m3，弹性模量K=1.95×105MPa，泊松比γ=0.247；钙质外壳选用塑性材料，密度ρ=2.6×103kg/m3，弹性模量K=5×104MPa，泊松比γ=0.3；藤壶胶选用粘弹性材料，密度ρ=1.19×103kg/m3，体积模量K=100 MPa，模型总共划分12 162个单元和15 405个节点。接触选择带失效的接触命令CONTACT_AUTOMATIC_SURFACE_TO_SURFACE_TIEBREAK。刀具与藤壶胶和钙质外壳选择自动接触命令CONTACT_AUTOMATIC_SURFACE_TO_SURFACE，并创建4个接触组。对基底和刀具施加边界条件，限制基底底面的6个自由度，将底面固定，并对刀具施加水平方向强制运动，并设定刀具X轴水平运动速度为-0.7 m/s。

图11 藤壶仿真示意图Fig.11 The simulation diagram of barnacle

通过仿真计算，得出藤壶粘附力的曲线、刀具水平和竖直方向上切削分力曲线，并对2个结果与理论曲线进行对比分析。

如图12所示，藤壶的粘附力的仿真曲线与理论曲线整体趋势相同，共同随着刀具进给位移增大而逐渐减小，仿真曲线略有波动。以具有代表性的2点A和B举例，分别代表与理论曲线相差的最大值和最小值，A点的最大相对误差为15%，B点最小相对误差为12%，C点的相对误差值处于最大值与最小值之间，平均误差控制在15%以内，与理论分析基本吻合。

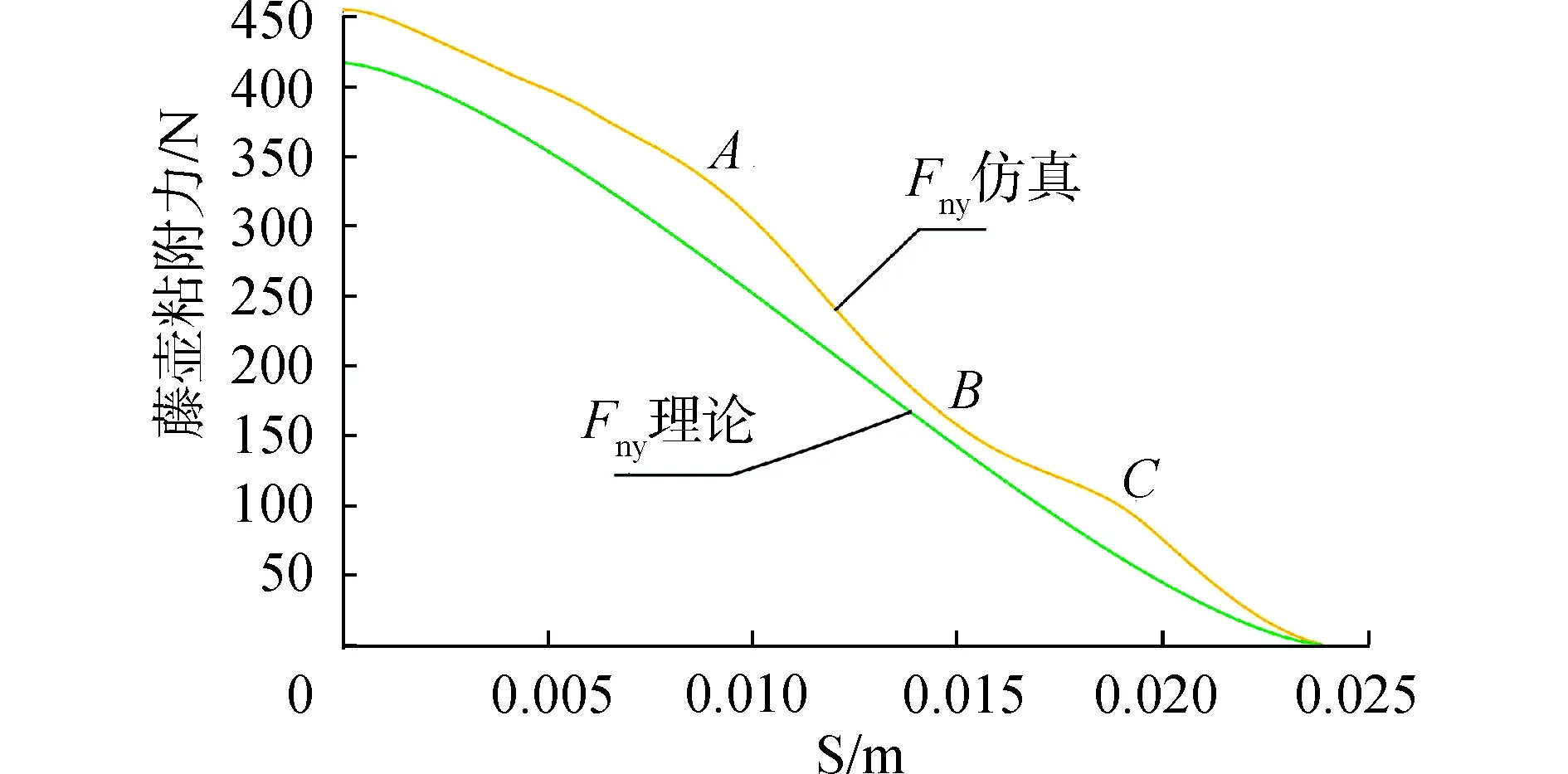
图12 藤壶粘附力仿真与理论拟合Fig.12 Simulation and analytical results of barnacle adhesion force

FH和FV的理论与仿真曲线拟合效果如图13所示。仿真曲线与理论曲线整体趋势保持一致，随着清除藤壶过程的不断进行，藤壶粘附力不断减小，作用在刀具上的FH越来越小，仿真曲线与理论曲线相交于D点，虽然仿真曲线体现上下波动，但是波动幅度较小，且相对误差在10%以内；FV仿真曲线与理论曲线趋势相同，吻合程度比FH曲线好，相交于E点；总体上，竖直与水平剪切力的仿真曲线与理论曲线相对误差在10%以内。通过仿真计算与理论曲线的拟合，对比及验证，证明了本文理论的正确性。存在误差的原因可能是理论值中假设刀具绝对锋利且不考虑刀具后刀面的摩擦，而实际仿真模拟的过程中，都是不能避免所造成的。