谐波减速器礼帽形柔轮应力应变分析与参数优化*

（江苏科技大学 镇江 212000）

1 引言

自1965年美国工程师Musser发明了第一代谐波减速器以后，谐波减速器就开始投入了实际应用［1］。与传统减速器相比，谐波传动具有精度高、结构紧凑、重量轻、减速比高和传动精度高等特点，使其被广泛应用于航天航空、机器人、精密机床、仪器仪表等领域［2］。由于行业的发展，各领域对谐波减速器的要求越来越高，谐波减速器轴向尺寸的减小，使得柔轮所受的应力急剧上升。而谐波减速器主要失效形式就是柔轮的破坏，由于柔轮齿圈结构上的非线性以及柔轮变形上的非线性，所以一直以来也无法精确计算柔轮在波发生器作用下产生的应力［3］。

随着有限元技术的发展，许多学者借助有限元软件总结了柔轮的应力应变规律。邢静忠利用有限元技术发现了礼帽形柔轮相较于杯形柔轮，负载工况引起的等效应力增幅更小［4］。彭盼道利用有ANSYS Workbench和正交试验法优化了柔轮双圆弧齿形的参数［5］。张世民利用ANSYS得出了不同负载对短杯柔轮的应力位置影响不大［6］。邓娟利用有限元得到柔轮厚径比和筒体长度对柔轮的影响规律，然后利用Matlab对试验数据进行曲线拟合，证明了理论计算的正确性［7］。

目前对于谐波减速器柔轮的研究主要集中在短杯形柔轮，而对礼帽形柔轮的研究不多。随着行业的发展，谐波减速器负载要求的提升，礼帽形柔轮在负载增加的情况下所受应力的增幅远远低于杯形柔轮的增幅［8］，这对柔轮的寿命和稳定性有着至关重要的影响，所以礼帽形柔轮更适合在大负载工况下的应用。但是礼帽形柔轮的空载情况下的应力远大于杯形柔轮，所以对礼帽形柔轮空载时的应力研究十分必要。

2 柔轮有限元分析

2.1 柔轮与波发生器几何模型

礼帽形柔轮结构图简图，如图1所示。现以工程中某型号柔轮为分析对象，其几何参数：筒长l=21.1mm，柔轮筒壁厚h0=0.37mm，覆板厚度h=0.37mm，筒内半径r0=16.95mm，d0=2r0=-33.9mm，筒底与覆板过渡圆角半径r1=1.78mm，柔轮轮齿宽b=7mm。

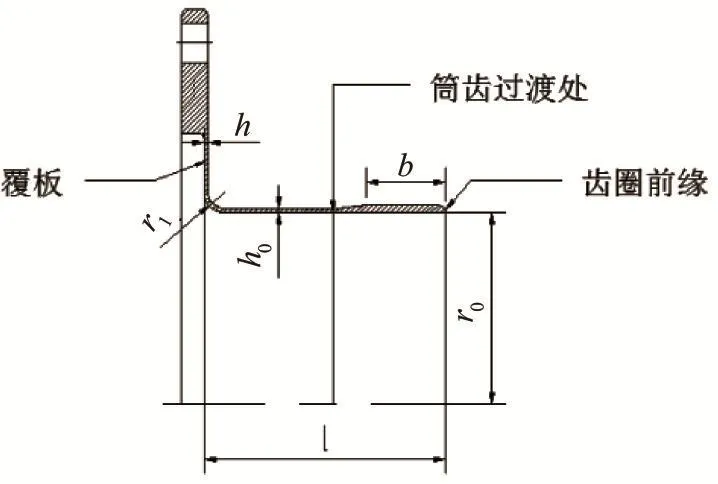
图1 礼帽形柔轮结构简图

本文波发生器选用椭圆波发生器，根据文献［7］椭圆波发生器的计算公式：

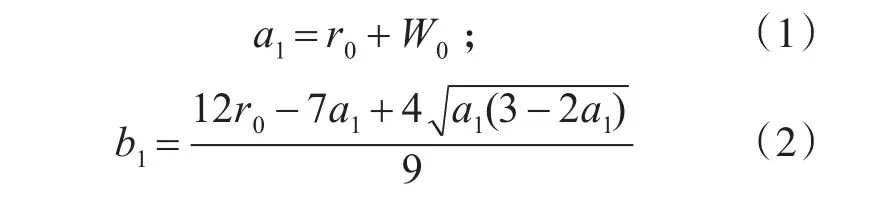
式（1）和式（2）中a1、b1分别为椭圆的长半轴和短半轴，W0是最大径向变形量，本工程实例中最大径向变形量为一个模数m=0.219。

2.2 应力应变计算

采用SolidWorks软件对柔轮和波发生器进行三维建模，然后将模型导入到ANSYS Workbench16.0有限元软件中进行计算。根据实际工程实例，柔轮的材料为40CrNiMoA合金结构钢，弹性模量为209GPa，泊松比0.295；波发生器的材料为40Cr，弹性模量为211GPa，泊松比为0.277。ANSYS Workbench中刚体为目标面（target），可变形面为接触面（contact），所以我们这里设置波发生器外圈为目标面，柔轮内圈为接触面；覆板底面施加固定约束，波发生器内孔施加轴支撑约束。在几何上，柔轮的最大径向变形量与厚度之比大于0.2，属于大挠度几何非线性问题［9］，所以需要在分析设置中打开大变形和弱弹簧选项，采用拉格朗日算法求解。覆板底面施加固定约束，波发生器内孔施加轴支撑约束。有限元模型如图2所示。

图2 礼帽形柔轮有限元模型

3 柔轮应力应变分析

3.1 柔轮应变分析

3.1.1 轴向应变分析

为了研究柔轮轴向应变的变化规律，我们选取了波发生器长轴、短轴以及长短轴之间45°处三个位置来观察它们的轴向应变。其结果如图3所示。

图3 轴向应变分布图

图3中横坐标为距离齿圈前缘的距离，齿圈前缘位置如图2中所示。从图3中可以看出，最大变形出现在波发生器长轴与柔轮接触处，最大形变量为0.275mm。并且轴向应变与距离齿圈前缘距离成线性规律，这与文献［9］中的试验结果是一致的。并且从图3中可以看出波发生器长轴处柔轮的变形量大于短轴处柔轮的变形量大于长短轴之间45°处柔轮的变形量。

3.1.2 径向应变分析

本文选取了如图2中所示的齿圈前缘处、筒底倒角处以及柔轮筒与齿间过渡处这三个位置来研究柔轮径向应变的。如图4所示，柔轮径向应变分布呈现规则的花瓣状。柔轮三处最大变形量均出现在与波发生器长轴接触的地方，最小变形量出现在波发生器长轴与短轴之间，齿圈前缘变形量大于筒齿过渡处变形量大于筒底倒角处变形量。

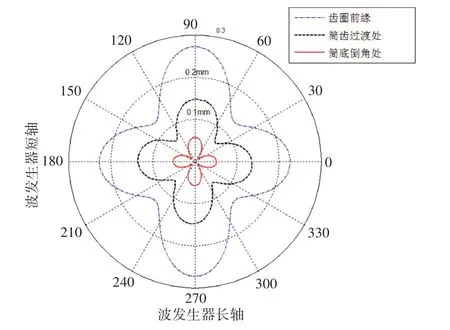
图4 柔轮径向应变分布

3.2 柔轮应力分析

3.2.1 轴向应力分析

接着我们对柔轮的应力进行分析，图5为柔轮轴向应力分布图，和分析应变一样，选取了波发生器长轴、短轴以及长短轴之间45°处三个位置来观察它们的轴向应力。从图5中可以明显地看出，柔轮三个位置等效应力均集中在齿圈前缘和筒底倒角处，筒底倒角处应力最大。波发生器长轴位置距离齿圈前缘5mm处应力发生波动是由于与波发生器接触导致的应力集中。齿圈前缘应力集中是由于柔轮受波发生器影响被迫挤压变形，齿圈前缘变形量大，导致应力集中，短轴处齿圈前缘的应力是三个位置中最大的。

图5 柔轮轴向应力分布图

3.2.2 径向应力分析

从分析轴向应力分布图中可以知道柔轮应力主要集中在齿圈前缘和筒底倒角处，于是我们选取这两个位置处的截面并观察对其径向上应力变化规律，这两个位置的径向应力分布图如图6所示。从图6中可以清楚的看出最大等效应力出现在波发生器长轴筒底倒角位置，其值为538.52MPa。在波发生长轴方向周围，筒底倒角应力普遍大于齿圈前缘应力。而在波发生器短轴方向周围，齿圈前缘处应力普遍要大于筒底倒角处应力，但是波发生器短轴方向上最大应力仍然出现在筒底倒角处。

图6 柔轮径向应力分布图

将工程实例中的样机与有限元模型进行对比，工程实际中的柔轮失效情况如图7所示。从图7中可以看出，样机柔轮在筒底与覆板过渡处发生断裂，这与有限元计算结果一致。

图7 礼帽形柔轮样机失效图

4 柔轮结构参数优化设计

4.1 正交试验设计

正交试验设计是研究多因素多水平的一种设计方法，能根据正交性从全面试验中挑选出部分代表性的点进行试验，从中挑选出最优水平组合，是一种高效率、快速、经济的试验方法［11］。

此次试验，以降低礼帽形柔轮所受最大应力为目标，进行正交试验设计，分析长径比l/d0，齿宽b，覆板厚与柔轮壁厚比h/h0，以及筒底与覆板过渡处圆角半径r1的大小对柔轮最大应力的影响。基于不改变柔轮内径的原则下，根据文献［12］中所述，选取每个因素的3个水平，采用四因素三水平，试验如表1所示。

表1 四因素三水平表

四因素三水平表选用L9（34）型正交试验表，一共9组试验，如果不用正交试验，将各水平试验全做完需要81次试验，大大减少了工作时间。

4.2 正交试验结果处理与分析

根据正交实验表中所给出的试验方案，选取方案中的水平组合，在SolidWorks中建立九个试验中新的礼帽形柔轮几何模型，因为这里的因素是在柔轮内径不变的原则下选取的，所以波发生器的几何模型不需要改动。再将新的几何模型分别导入到ANSYS Workbench中进行有限元分析，得出每组试验的最大应力，试验结果如表2所示。

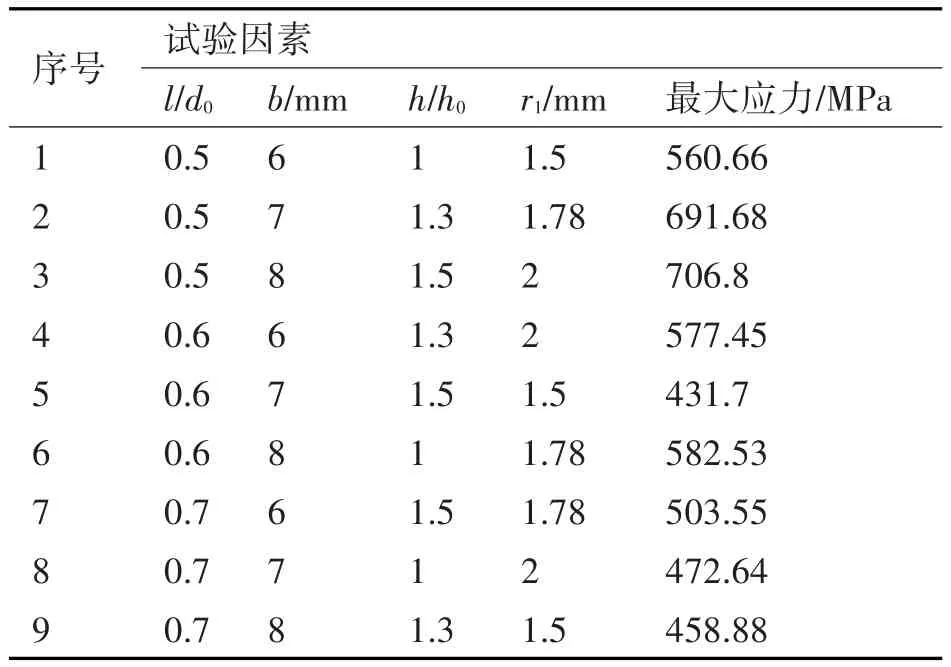
表2 正交试验表

从表2中可以看出第五组试验最大应力比第二组试验应力值减小了275.1MPa，差距十分大，由此可见结构参数优化的必要性。接下来我们对试验结果采用直接分析法进行分析，就可以得出最佳的水平组合。首先需要计算各因素各水平的平均值Ij，再分别计算各因素平均值的极差Rj，根据极差可以判断各因素对试验结果的影响大小，平均值和极差的计算如表3所示。

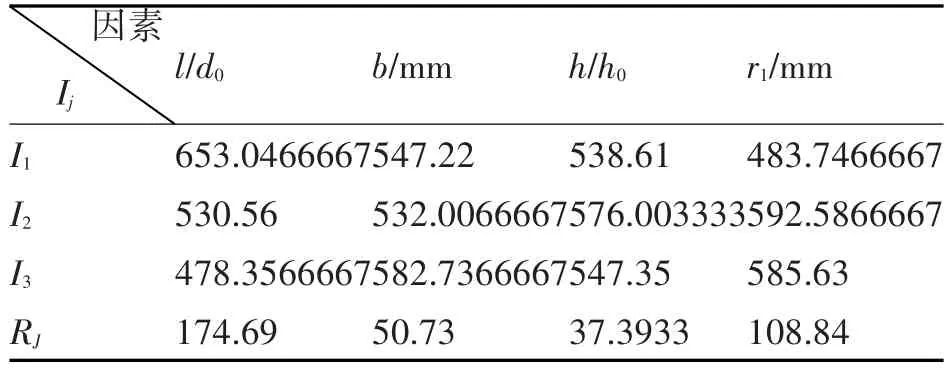
表3 正交试验结果表

由表三可知长径比l/d0的第三个水平I3应力值最小，齿宽b的第二个水平I2应力值最小，覆板厚与柔轮壁厚比h/h0的第一个水平I1应力值最小，筒底与覆板过渡处圆角半径r1的第一个水平I1应力值最小。本试验中选取最优水平解为l/d0取0.7，b取7mm，h/h0取1，r1取1.5。将试验最优解进行模型创建和有限元求解，参数优化后的柔轮最大应力变为了411.21MPa，比原来的工程实例样机最大应力减少了23.64%。

5 结语

礼帽形柔轮最大应变出现在波发生器长轴与柔轮接触处；波发生器长轴处柔轮的变形量大于短轴处柔轮的变形量大于长短轴之间柔轮的变形量；齿圈前缘变形量大于筒齿过渡处变形量大于筒底倒角处变形量。

礼帽形柔轮等效应力集中在齿圈前缘和筒底倒角处，最大等效应力出现在波发生器长轴方向上的筒底倒角处；波发生器短轴方向上，齿圈前缘应力集中较大。

礼帽形柔轮的结构参数的不同水平组合产生的最大应力极差较大，可以通过优化尺寸结构，来降低柔轮最大应力。

通过正交试验，降低了工程实例中的柔轮参数从l=21.1mm、齿宽b=7mm，覆板厚度h=0.37mm，筒底与覆板过渡圆角半径r1=1.78mm，修改至l=23.73mm，齿宽b=7mm，覆板厚度h=0.37mm，筒底与覆板过渡圆角半径r1=1.5mm，应力值从538.52MPa将至了411.21MPa，降低了23.64%，使柔轮的性能得到了很大的改善。

礼帽形柔轮的长径比以及筒底与覆板过渡圆角半径是最大应力的敏感因素，在工程设计中需要着重注意，齿宽和覆板厚度并不是礼帽形柔轮的最大应力的敏感因素。