多机移动条件下飞行甲板路径规划研究*

（海军航空大学青岛校区 青岛 266041）

1 引言

舰载机在航母甲板的移动是航母安全作业的重要隐患，其移动效率也制约着航母战斗力的生成。由于航母飞行甲板与机库甲板的高度复用性，舰载机在甲板的调运路径应进行合理规划，避免碰撞的同时提高转运效率，这也是实现舰载机自动牵引的核心问题。

路径规划问题较早应用于自主移动机器人［1～3］，通过自动推理、全局规划、移动控制等过程，实现机器人的自主导航移动。在舰载机应用方面，刘亚杰等［4］针对舰载机转运过程中的碰撞问题，采用栅格法表示舰载机位置信息，检测路径是否安全，其转运路径需要人工设置。高杰等［5］针对航母甲板舰载机调运过程问题，采用混合整数规划方法对移动路径优化，采用“碰撞区域”方法评价路径合理性，从而生成所需路径。张竞等［6］着力解决甲板环境下的舰载机路径规划问题，主要针对舰载机在牵引模式下，整个运动系统的路径优化。本文考虑到航母飞行甲板与机库甲板通常配备多个转运小组，采用新的碰撞检测方法，研究多机转运条件下的飞行甲板路径规划问题。

2 舰载机飞行甲板路径规划建模

2.1 舰载机转运过程描述

在航母甲板转运过程中，当确定了舰载机的初始停机位和目标停机位后，我们应能够按照一定的转运原则，使整个转运过程用时最短，如果是多机转运，则应按照最后一架飞机到达目标停机位的时间作为最终用时，其具体过程如图1所示。

图1 双机甲板转运路径

图1中A1与A2为初始舰载机停机位，A3与A4分别是前两飞机的目标停机位。B1与B2为障碍机位，阴影部分为障碍建筑。整个转运过程应从离开初始机位开始计时，到最后一个到达目标机位的舰载机为止结束计时。每一架飞机可以有任意种行走路线，图中只列出其中四条转运路线，可以明显看出，转运路线重复度高。当只有单架飞机转运时，只需考虑障碍物的避碰就可以，因此最短路径即为用时最少的路径。但多架飞机转运时，我们需要综合考虑避碰、等待用时等因素，这时不能以路径长短作为最优参考路线，应该以作业时间长短作为参考指标［7～8］。

2.2 路径规划建模

根据上述作业流程分析，可以将舰载机甲板移动过程描述为求解带有约束条件的飞机甲板转运用时计算问题。针对飞行甲板多机转运任务建模，为保证模型可行性，应进行如下前提假设：

1）牵引作业移动速度匀速恒定，不超过安全限速。

2）牵引作业转弯时，按设计角度自行转弯，不超过安全角度。

3）牵引进入停机位一次成功，不计算调整时间。

其表达式如下所示：

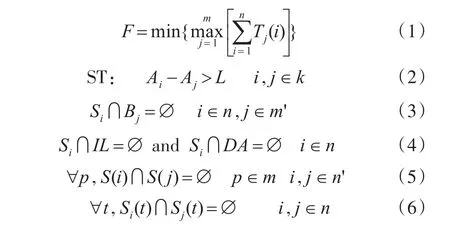
式（1）中n为每套转运方案的路径数量，m为每次转运的舰载机数量，T（i）表示每段转运路径所用时间，表达式含义为求各转运方案中用时最少的方案；式（2）中L为最大舰载机的最大尺寸，k为每套方案中的舰载机初始机位与目标机位的总数量，Ai表示第i架舰载机的位置，表达式含义为所有初始机位与目标机位不干涉，相距一个机位以上；式（3）中m'表示障碍飞机数量，n表示转运路径数量，Si表示第i条转运路径，Bj表示第j架障碍飞机位置，表达式含义为转运路线与障碍飞机不相交；式（4）中n表示转运方案的路径数量，IL表示障碍建筑，DA表示甲板边缘，表达式含义为舰载机转运空间在甲板内部，且不占用建筑空间；式（5）中m表示每次转运的舰载机序列，n'表示同一架飞机的转运序列，S（i）表示第i条转运路径，表达式含义为对于同一架飞机的任意转运路径不相交；式（6）中t表示转运时间轴，n表示转运路径数量，Si（t）表示第Si条路径在t时刻的位置，表达式含义为任意舰载机在相同时刻的位置不同。

3 舰载机碰撞及等待计算

3.1 舰载机碰撞问题计算

舰载机在甲板的水平移动，考虑到转运作业的安全性问题，是不允许高低装备之间相互穿插经过的，所以，其整个移动碰撞问题可以理解为二维平面内的碰撞检测。目前平面碰撞检测方法主要采用“栅格法”和“包围盒法”。本文采用多边形包围盒法来近似描述舰载机轮廓，将预选的舰载机路径与包围盒相交测试，实现路径的避碰。

对于甲板面的舰载机，如图2所示，可以采用图3的多边形包围盒，舰载机直升机采用图4的多边形包围盒，其数学表达式可采用边序列的表达方法，分别为

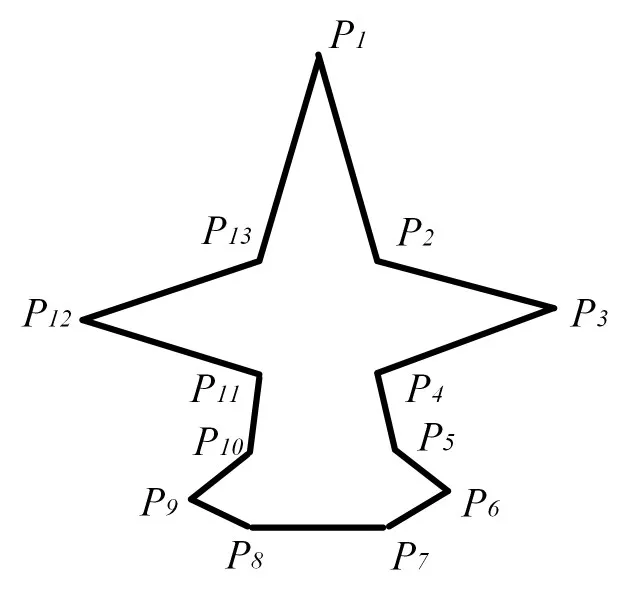
图2 舰载机轮廓

图3 多边形包围盒

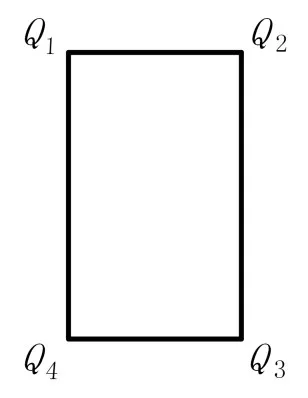
图4 直升机多边形包围盒

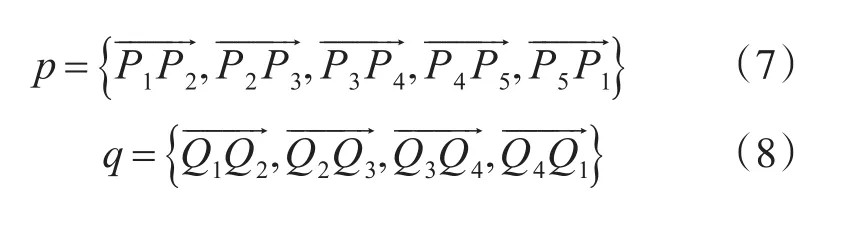
对于移动路径与包围盒的相交测试，可以采用多边形径向膨胀法。由于舰载机多边形包围盒是规则五边形，当包围盒沿预定路径移动时，其多边形的中轴线一定与路径重合，这时若移动多边形包围盒与障碍物多边形包围盒相撞，则其中轴线与障碍物多边形必定相交，也就是说预定路径与障碍物多边形各边的距离小于移动舰载机多边形的法向宽度，其检测过程如图5所示.

碰撞检测具体计算步骤可分为如下四步：

1）计算移动舰载机多边形法向宽度r，同时设置舰载机之间安全距离θ；

2）将障碍飞机各边向外平移r+θ，得到新的多边形q'；

3）将移动舰载机路径序列分别与q'的各边进行相交检测，如果任意一对边相交，将目标函数适应度值设为最大，循环跳出；

4）如果第3）步中各边全不相交，则进入下一障碍飞机的碰撞循环，重复1）～3）步骤。

3.2 舰载机碰撞等待计算

以上是对甲板固定障碍物的碰撞计算，其采取的策略为“绕行”方式，发生碰撞即排除路径。对于多机移动的碰撞问题，需要加入等待时间的计算。当两架飞机同时在甲板移动时，一方面需要避碰固定障碍物，另一方面需要相互避碰，这时应以总移动时间最短为目标，比较绕行所需时间与等待所需时间哪个更少，则采取哪种行走策略，其过程如图6所示。

图6 双机路径选择策略

A1和A2分别为初始停机位，A3和A4分别为前两飞机的目标停机位，B1为障碍飞机。选取S1为A1飞机的转运路径，选取S2和S3为目标飞机的转运路径。当A2飞机沿S2路径移动时，移动距离短，但需要等待A1飞机通过后才能继续前进，而沿S3路径移动时，移动距离长，但无需等待。

本文采用“离散路径、近距优先”的策略处理多机移动问题，一是在所有预选舰载机路径中设置两个转折点，各转折点间采用直线路径，在舰载机进入每一段路径前，先判断该路径碰撞情况再驶入，这样可以减少总的路径等待时间；二是按照预选路径最短的原则，将舰载机移动顺序进行排列，赋予舰载机行动优先级，这样可以避免舰载机的重复等待。移动舰载机之间的碰撞检测计算按以下步骤计算：

1）依次存储各飞机转运路径序列Sn，同时，为各飞机建立等待时间序列Tn，Sn与Tn应该一一对应。

2）根据预选路径长度，计算各舰载机转运优先级。

3）判断当前待转运舰载机优先级Ω，若Ω=1则无需进行等待时间计算，转入第7）步。

4）依次将本优先级舰载机各路径与Ω优先级以前的舰载机所有路径进行相交判断。

5）若在SΩ(i)路径相交，则计算该优先级以前舰载机经过该路径的时间t，同时计算Ω优先级舰载机经过SΩ(i-1)路径的时间t'，t-t'即为SΩ(i)的路径等待时间，计入TΩ，转入第7）步。

6）若在SΩ(i)无相交情况，记录SΩ(i)的路径等待时间为0，计入TΩ，转入第7）步。

7）计算SΩ优先级舰载机转运时间，同时加入等待时间TΩ。

8）转第3）步计算下一优先级舰载机转运时间。

4 舰载机路径规划计算

在舰载机初始位置与目标位置确定的情况下，每架舰载机路径选取两个中间转折点，转折点间采取直线路径的方式，则n架舰载机的路径规划问题就转变为n×2个路径点的组合优化问题。本文采用离散粒子群算法解决该问题［9～11］。该算法在多维空间多峰问题寻优、动态目标寻优及排列组合优化等方面有着速度快、解质量高、鲁棒性好等优点。

4.1 粒子编码

在离散粒子群算法中，我们将每一套路径方案编码为一个粒子，通过多个粒子之间不断竞争，追逐最优粒子，达到寻找最优方案的目的。每一个粒子的维度由舰载机的数量和中间转折点的数量决定，每一个中间转折点采用二维坐标(x，y)表示，则对于n架舰载机和2个中间转折点的路径方案，其每一个粒子编码可采用n×4维矩阵表示。

4.2 算法步骤

设置算法种群数量为D，最大迭代次数为N，对于4.1节中的编码方式，其算法描述如下：

1）算法初始化。设置初始种群，随机设置D个粒子的初始位置，初始速度。

2）针对初始种群，对粒子解码，采用第2节中的模型及第3节中的计算方法计算适应度值，确定历史最优粒子，全局最优粒子。

3）采用式（9）计算粒子速度，如果速度超过最大值，则取为最大值。

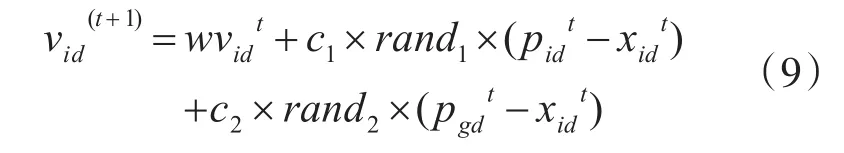
4）根据第3）步中的粒子速度，采用式（10）计算粒子位置，如果超过最大值，按照碰撞处理。

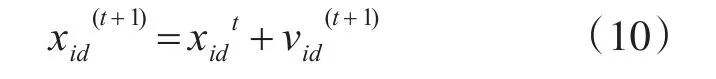
5）针对更新后的粒子，采用第2节中的模型及第3节中的计算方法计算适应度值，更新历史最优粒子，全局最优粒子。

6）判断是否达到迭代次数N。如果达到，输出计算结果；否则，转向步骤3）。

4.3 参数设置

设置种群数量D为50，确保随机采样率。设置最大迭代次数为100，后期根据迭代结果情况再调整。w为惯性权重，较大的w值有利于保证算法的全局性，较小的w值有利于保证算法的收敛性。本文采用动态惯性权重方式，前期具有较宽的搜索能力，后期具有较精确的寻优能力［12］，如式（10）所示。

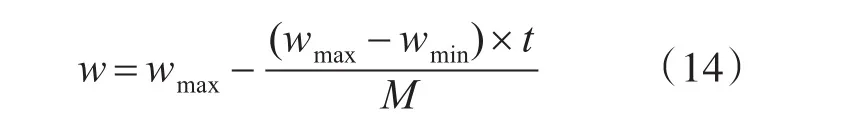
式中t表示迭代次数，wmax取为1，wmin取为0.2。c1和c2为学习因子，c1表示向自身历史最优粒子靠近的权重，c2表示向全局最优粒子靠近的权重，本文取c1为1.7，c2为1.9，保证算法全局性较高。

4.4 计算结果

采用Matlab7.1编程，利用图1中的舰载机布列任务进行测试，飞机转运速度按照4km/h计算，甲板总尺寸按照300m×70m计算，其所有飞机的坐标及机头角信息如表1所示。

表1 飞机坐标与机头角信息

计算结果如下：

1）连续优化十次，十次最优路线如图7所示，图中障碍物飞机周围虚线为按照3.1节中碰撞检测方法外扩后的轮廓线，由于机头顶点外扩距离过远，本文采用六边形描述，其外扩方法与前文描述一致。黑色实线为经过十次优化后的路径，都不与蓝色轮廓线相交，结果表明，本文所采用碰撞检测方法适用于多机甲板转运要求。

图7 十次最优的路线

2）连续优化十次，其最终最优方案如图8所示，十次转运过程的最优用时与等待时间如表2所示。最终最优路径行驶总用时为213.3s，其中，行驶等待时间为32.6s。十次最优结果的最大用时为227.2s，平均最优用时为218.5s，结果浮动范围相差不大。该结果表明，本文所采用碰撞检测方法及智能算法计算偏差小，全局收敛性好，没有陷入局部极小，可以用于飞行甲板多机转运辅助决策。

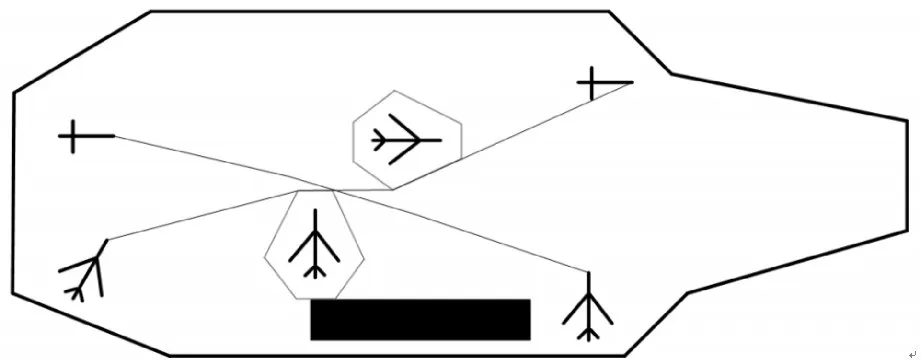
图8 双机转运最优路径

表2 十次转运的最优用时与其中等待用时

3）采用50个粒子种群，100次迭代循环，连续优化十次的迭代曲线如图9所示，所有迭代循环能够在70～80代之间完成收敛，收敛结果幅度较小。其结果表明，使用离散粒子群算法计算该碰撞检测问题，算法收敛速度快，收敛一致性好，迭代次数设置符合要求。

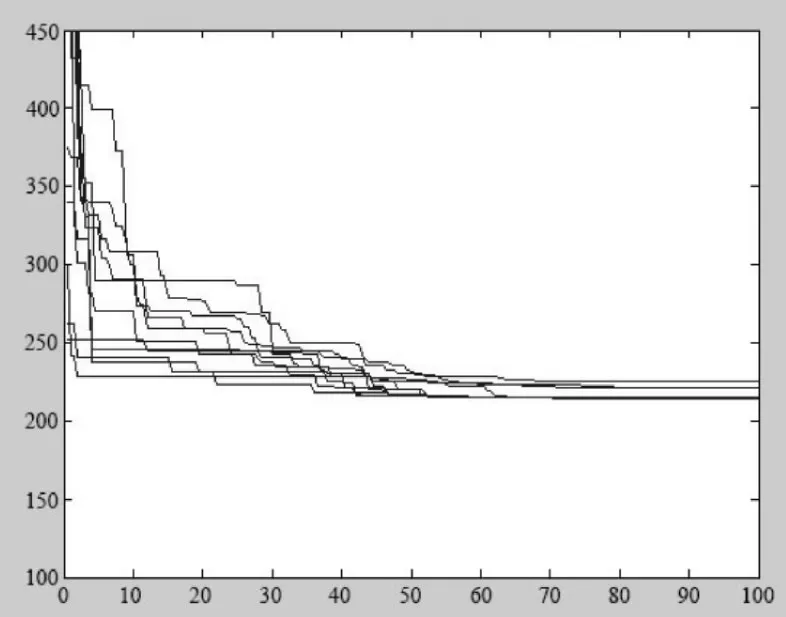
图9 十次迭代的收敛曲线

5 结语

本文研究了以碰撞等待时间为主要因素的飞机移动碰撞问题，采用离散粒子群算法求解多机转运条件下的甲板路径规划模型。通过对文中实例的验证，本研究给出的双机移动路径能够有效实现舰载机与固定障碍物的避碰，同时，也能够实现移动飞机之间的避碰与等待，给出了飞机等待时间。计算结果表明本研究符合实际规划需求，可以用于舰载机自动牵引的辅助决策。