基于变权TOPSIS方法的炮兵阵地优选方法*
2021-03-16
(陆军工程大学 南京 210000)
1 引言
炮兵是现代陆军主要的火力突击力量,在联合作战体系内仍占有重要地位。炮兵在作战过程中,需依据战场态势对阵地位置进行选择布置,良好的地形环境条件是炮兵分队展开作战行动、落实战斗决心、顺利完成任务的前提[1]。
炮兵阵地的选择需要考虑诸多的因素,炮兵的装备性能、战场态势的变化、战术原则的把握以及不同位置的地形环境条件等,都制约着炮兵的作战效能。这些制约因素涵盖地形地貌、气象水文、战场态势等多方面信息,信息的种类复杂数量庞多,综合分析的难度较大。当前,我军指挥员在炮兵部署决策上通常采用图上作业的方法。这种决策方法依据决策者的意识和经验,存在主观随意性,且缺少客观定量的依据,决策效率和决策科学性都难以得到保证,无法满足现代战争中对炮兵部署高效决策的需求。阵地位置选择是炮兵兵力部署决策的关键环节,整合其中涉及的各方面信息情报,分析炮兵阵地选择的主要影响因素,构建炮兵阵地优选的理论模型和方法,对提高指挥员的决策效率和决策的科学性,提升炮兵指挥的灵活性有着积极的意义。
2 阵地综合评价体系构建
2.1 评价体系的构建
炮兵分队的军事行动受环境因素、装备性能因素和战场态势因素三方面影响[2~3]。环境因素是指自然环境条件对军事行动的影响,装备性能因素主要考虑装备的数量规模和技术性能等,战场态势因素是指敌我友邻的部署对于炮兵分队行动的影响。这些因素在不同的层次上制约着炮兵分队作战行动。综合分析上述三方面对炮兵作战行动的影响,文章从利于机动、利于生存、利于射击三方面选取炮兵阵地评价指标,构建评价体系如图1所示。

图1 炮兵阵地综合评价体系
2.2 指标的量化方法
炮兵阵地综合评价体系包含诸多不同性质、不同择优区间的指标,指标间具有明显的不可公度性。在指标的量化上,可引用模糊数学中模糊集和隶属度的概念进行规范化处理。经典集合论中,元素x和集合A的关系界限分明,只有属于、不属于两种情况,模糊数学中的隶属函数是将上述特征作适当推广,将二值逻辑{0,1}推广至连续闭区间[0,1]。
设是论域X到[0,1]的一个映射,即
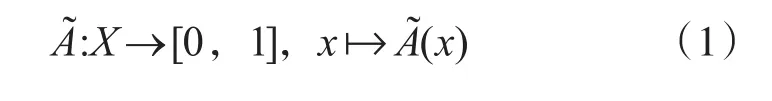
称是论域X上的模糊集,成为模糊集的隶属函数。对于论域中的任一元素xi,都有[0,1]区间上的唯一实数与之对应,即为元素xi对于模糊集的隶属度,表示该元素属于模糊集的程度。时,表示元素xi完全不属于模糊集。反之,时,表示元素xi完全属于模糊集。文章将模糊集与隶属度的概念引用到对炮兵阵地单项指标的评价上,对各指标构建模糊集,将指标的原始数据作为评价的内涵,将指标状态是否符合战术条件要求作为评价的外延,并用隶属度表示。其中,0表示完全不适合、1表示完全适合,而后根据各指标对阵地选址影响机理的不同分别确定阈值,建立隶属函数。在构建完所有指标的隶属函数后,也完成了指标的归一化处理和同趋势化处理[4]。
2.3 指标权重的确定
权重代表指标间的相对重要性,文章采用层次分析法计算指标的权重。层次分析法(AHP)是20世纪70年代由美国匹兹堡大学教授T.L.Saaty提出的,其基本思想是将复杂的问题依据决策准则逐层分解,并用递阶层次结构表示,从而将复杂的问题进行简化[5]。权重计算的基本方法是对同一准则层下的各个指标,采用适当标度进行两两对比,构建各准则层的判断矩阵,从而计算指标的权重。层次分析法计算简便,适用于没有网络结构特性的系统评价问题[6]。运用层次分析法时,选用不同的标度得到的判断矩阵也各不相同,标度的选择在很大程度上影响着权重计算结果的合理性[7~8]。在炮兵阵地选择问题上,可采用9/1~9/9标度构造判断矩阵,并采用“根法”对指标权重进行求解。本文以表1中的权重作为综合评价基本依据。

表1 指标权重
3 基于变权的TOPSIS综合评价方法
3.1 变权理论
变权理论的基本思想是根据指标值状态的变化调整指标在系统中的权重,使指标的加权值能够更为合理地反映该项指标在整个评价系统中的作用[9]。运用常权综合方法对炮兵阵地进行评价时,尽管通过权重衡量了指标在系统中的重要程度,但权重仅能反应指标在状态良好时对整个系统的影响。当个别指标存在严重缺陷导致方案整体不可行时,这种缺陷无法通过常权分析表达出来。在变权综合评估法中,加入了对指标状态的考虑,指标的权重根据指标自身状态的好坏做出适当的调整,因而能够更加客观地反映出该项指标对于整个评价系统的影响。
设指标权重向量为W=(w1,w2……,wn),状态向 量X=(x1,x2……,xn) ,设S(X)=(S1(X),S2(X),…,Sn(X))为X的状态变权向量。指标的变权即Wi(X)可按下式确定:
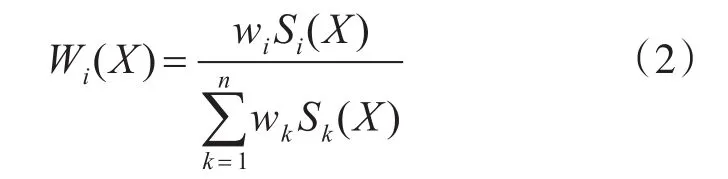
本文采用指数型变权方法[10],构造变权向量如下:

上述公式中,均衡系数α决定了变权类型和变权力度,α>0时为惩罚型变权,α<0时为激励性变权,α=0时为常权。文章取均衡系数α=2。
3.2 基于变权的TOPSIS方法评价步骤
TOPSIS(Technique for Order Preference by Similarity to Ideal Solution),称为逼近于理想解的排序方法,是由Yoon和Hwang提出的一种适用于多方案决策的评价方法[11]。基于变权的TOPSIS炮兵阵地综合评价方法可按照如下步骤进行[12]。
1)构造初始矩阵
设有m个阵地备选方案,xij为第i个方案中第j个指标的隶属度,构建初始矩阵A如下:

2)构建理想方案与负理想方案
由于所有的评价指标均已隶属度的形式表示,此处设绝对理想方案A*为A*={ }1,1,…,1 ,设绝对负理想方案A0为A0={ }0,0,…,0 。
3)计算各备选方案变权权重
如前文所述,各备选方案的变权权重可按照式(2)和式(3)计算。
4)按下式计算各备选方案至正负理想方案的加权欧式距离

5)按下式计算各备选方案的贴近度,由大到小形成决策依据

4 实例分析
以表2列举的6处阵地备选方案为算例,表中所列数据为各指标换算为隶属度的状态值。

表2 备选方案与指标隶属度
根据第三章节提出的方法,分别运用常权和变权的方法计算6处备选方案的综合贴进度,计算结果如图2所示。

图2 常权、变权综合评价对比图
图2列举了基于常权、变权的综合评价计算结果,通过结果对比可以看出,在运用TOPSIS法进行综合评价时,引入惩罚型变权会使总体结果变得相对保守,由图中各方案的变权贴近度可以直观地得出所有方案的排序为 S5>S1>S2>S4>S3>S6。图中,阵地1、阵地3、阵地5无论采用哪种赋权方式,其综合贴进度的变化均不大,说明这三种方案中指标的状态水平相对均衡,没有存在明显的短板,而阵地2、阵地4、阵地6在采用不同的赋权方式时综合贴进度变化明显,说明这三种方案存在个别短板,其中备选阵地2在采用不同的评价方法时,贴近度变化最大。图3为该方案在采取变权综合评价时指标权重的变化情况,从中可以看出,该方案下指标C21、C22的变权权重较常权增长明显,C31的变权权重有所增长,其余指标变权权重均有所下降,依据惩罚型变权的定义可知,这三项指标对比其他指标状态较为恶劣,是该方案的制约因素。在变权综合分析中,指标的状态水平也会作为综合评价的依据,使结果比采用常权分析更加客观准确,能够使决策者获得更多的决策信息,更适用于对炮兵阵地选址决策的综合评价。
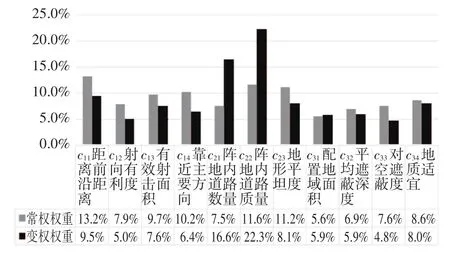
图3 备选方案2指标权重对比
5 结语
本文主要研究了基于变权TOPSIS方法的炮兵阵地优选方法,梳理了炮兵阵地综合评价体系和指标量化方法,将变权理论与TOPSIS法相结合,提出了基于变权TOPSIS的炮兵阵地综合评价方法。该方法在评价过程中考虑了指标状态对系统整体的影响,能够使评价结果更加客观真实。
