基于3D Voronoi模型形状不规则度组合梯度泡沫金属的动态冲击力学性能研究

胡和平,刘希文,张晓阳*,孙耀威

(1.南华大学 土木工程学院,湖南 衡阳 421001;2.南华大学 计算机学院,湖南 衡阳 421001)

0 引 言

泡沫金属作为一种新型的工程材料，兼顾了金属材料和多胞结构的特点，具有质轻、高比强度和刚度、吸能效率高等优点[1-3]，作为一种功能和结构一体化的新型轻质材料，具有广泛的应用前景，也在越来越多的领域有着重要的应用[1-4]。因为其内部结构具有大量孔隙，所以具有很好的能量吸收效果，但在相对密度相同的情况下泡沫金属的力学性能仍有很大的离散性。所以研究细观结构对泡沫金属力学性能的影响研究是很有必要的，其能量吸收特性的理论分析也有待探究完善。

目前，有许多学者使用实验和数值模拟相结合的方法研究泡沫金属的抗冲击性能和吸能效率[5-9]，此外，还研究了泡沫金属不同冲击荷载作用下的应变率效应和惯性效应，为泡沫结构的优化设计提供了理论基础。也有许多学者考虑使用改变相对密度的方法研究梯度泡沫金属的力学性能[10-11]，结果发现梯度泡沫金属表现出优异的能量吸收特性，并在实际工程中得到生产和应用。当密度沿一个方向连续变化时，这种类型的多孔材料被称为密度渐变泡沫金属。通过结构创新和优化生产使用这种类型的泡沫结构，将会显著提高其能量吸收能力并发挥防护作用。

有研究表明，即使泡沫结构的孔隙率和相对密度一致的情况下，它们的力学性能也具有很大差异[12-13]，泡沫金属细观结构不规则度尤其是胞元的几何不规则度的影响最为重要。L.Q.Tang等[14]拓展应用到三维Voronoi模型并提出了形状不规则度和尺寸不规则度参数，研究准静态下泡沫金属的压缩力学性能。Y.D.Wu等[15]基于二维Voronoi结构发现不规则度梯度变化会显著影响平台应力和能量吸收，负梯度(形状不规则度由大到小变化)的泡沫金属具有最优的能量吸收特性。目前尚未有基于三维Voronoi结构，开展形状不规则度组合梯度泡沫金属冲击吸能特性的研究。

Voronoi随机模型[16-17]由于能更合理的描述实际泡沫材料内部复杂、无序的细观结构，同时能更加方便快捷的研究泡沫材料的力学响应，因此Voronoi模型被广泛应用于泡沫材料的力学性能研究。

基于形状不规则建立的新型梯度泡沫与传统梯度泡沫不同的是，它是通过改变泡沫金属的内部细观结构(胞孔尺寸)而不是相对密度来获得新的力学性能，相比密度梯度泡沫金属的质量分布不均匀，它的质量分布更合理且减轻了重量，同时结合3D打印技术为泡沫梯度材料的优化设计提供科学指导。

本文将采用三维Voronoi结构材料，以两种不同形状不规则度进行组合，构造了一种新型的组合梯度泡沫金属，以有限元数值模拟的方法对梯度模型施加准静态和不同速度的冲击载荷，通过分析它的变形特征、承载能力和能量吸收特性来研究其冲击力学性能。

1 3D-Voronoi模型的建立

在本文中，梯度泡沫金属模型由沿x轴方向的两个不同形状不规则度(分别是0和2)组合。根据L.Q.Tang等[14]基于Voronoi模型的压缩结果，得出泡沫金属的屈服应力主要受形状不规则度的影响，几乎不受尺寸不规则度的影响，在同等相对密度和平均胞孔尺寸条件下，泡沫越规则平台应力就越大。为了探究其力学性能，创建了相同相对密度下，由两个形状不规则度组合的四个梯度模型，如表1所示。

表1 形状不规则度组合模型Table1 Combined model of shape irregularity

1.1 具有不同形状不规则度Voronoi模型的生成

首先，利用voro++程序在0.03 m×0.03 m×0.03 m的三维空间里面随机生成1 500个种子，且沿x轴方向均分成三块区域同时保证每个区域的种子数量大致相同，通过调整任意两个种子点的距离获得0和2两个形状不规则度组合的3D Voronoi结构。三维Voronoi模型每个胞孔的形状不规则度Ra的定义[14]

(1)

其中，Vi和Si分别是胞孔的体积和表面积。

然后使用Hyper Mesh软件进行网格的划分以及网格的检查和删除，为了提高计算效率和获得准确结果把网格采用S3R和S4R单元。

1.2 建模

把修改完毕的模型导入ABAQUS，首先查询模型的总表面积计算得到胞壁厚度，各个模型的相对密度都同为0.14。梯度泡沫金属的基体材料假定为纯铝且设定为理想弹塑性，泡沫金属基体材料密度为2 700 kg/m3，弹性模量为70 GPa，泊松比为0.33，屈服强度为110 MPa。为了方便施加荷载模型在x轴加载方向装配了解析刚体，模型和解析刚体之间采用表面与表面接触，设置分析步(类型为动力显示)和相互作用(采用两种相互作用类型)以及施加恒定的速度荷载(1 m/s～150 m/s)。如图1所示，将加载模型的x轴一端固定，另一端进行冲击压缩，并分别采用从正向冲击(x正方向往负方向)和负向冲击(x负方向往正方向)进行对比，同时还进行了准静态的压缩。

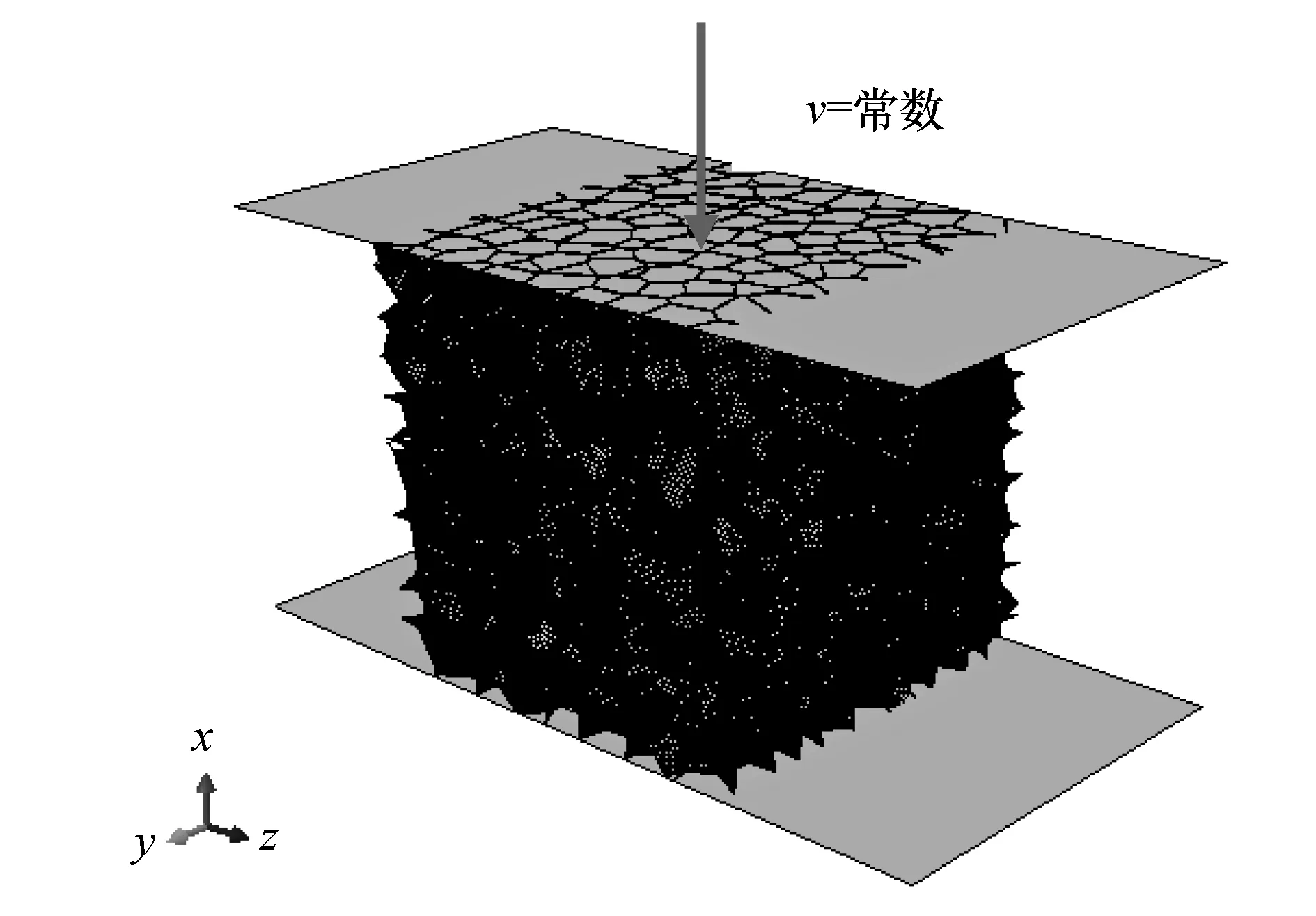
图1 正向冲击加载模型Fig.1 Positive impact loading model

1.3 模拟结果合理性验证

泡沫金属模拟结果是否合理的重要评判标准之一是伪应变能与内能的比值，它的比值越小说明结果的合理性越高，为了保证计算结果的合理性伪应变能与内能的比值不能超过10%。如图2所示是v=30 m/s冲击压缩下四个组合模型的伪应变能曲线，从图2中可以看出伪应变能比值都没有超过10%，所以说明模型的数值模拟结果是合理可信的。

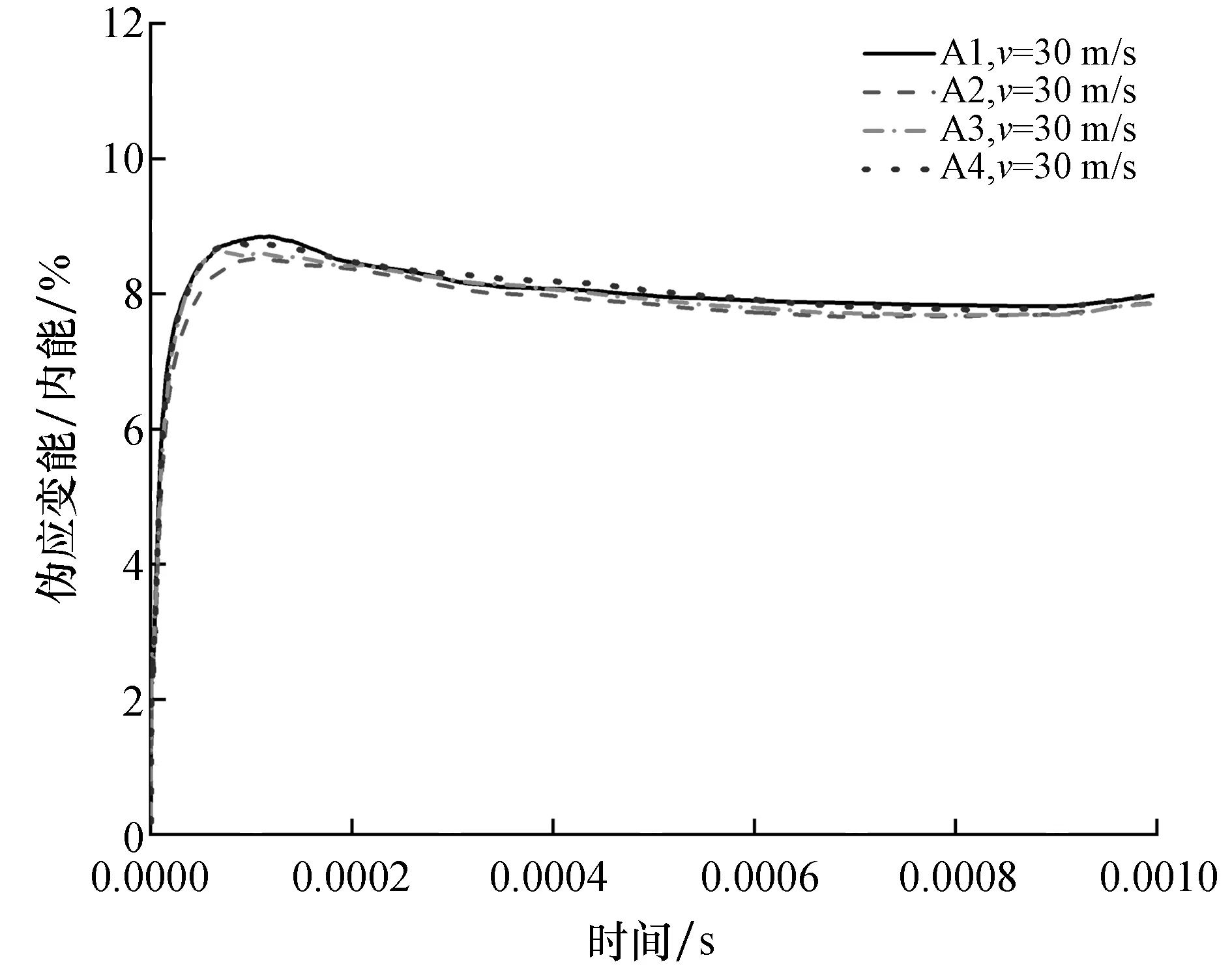
图2 伪应变能比值曲线Fig.2 Artificial strain energy to internal energy

2 结果与讨论

2.1 不同冲击速度下泡沫金属的变形

泡沫金属的冲击压缩随着冲击速度的增加会呈现出不同的变形模式，根据变形情况的不同可以大致分为三种变形模式：准静态均匀模式、过渡模式和冲击模式[18]。

在准静态荷载(速度为0.015 m/s)的作用下，泡沫金属发生均匀变形模式，如图3(a)所示，泡沫金属模型两端的受力大小和变形情况大致相同，压缩初期靠近加载端的胞孔会先受力发生变形，并且随着继续压缩会出现破坏变形带，这种破坏带会逐渐由加载两端向中间扩展。如图3(b)所示，当冲击速度为1 m/s时，泡沫金属的变形会首先出现在冲击端，变形由冲击端压缩密实并往固定端靠近，最后整个模型被压缩成I字形。如图3(c)所示，当冲击速度为30 m/s时，冲击端最先出现压缩破坏，而固定端几乎没有变形，在加载初期冲击端的胞孔就会被压溃破坏且伴随有破坏碎块飞出，胞孔的破坏会导致其它相连的胞孔相继塌陷破坏，破坏压溃带由冲击端向固定端扩展直至整个模型被逐层压溃破坏，这表明随着速度的不断增加，局部变形破坏越明显。如图3(b)、(c)、(d)、(e)所示可以看出，加载方向的改变对这种不规则度的梯度组合模型的变形模式几乎没有影响。

图3 A2模型不同加载速度和加载方向下的变形图Fig.3 Deformation diagram of A2 model under different loading speeds and loading directions

2.2 荷载-位移曲线

不同形状不规则度组合梯度模型的准静态压缩名义应力-应变曲线如图4所示，加载速度为0.15 m/s。平台应力和压实应变常作为体现泡沫金属压缩力学性能的两个重要参数，从图中可以看出四个模型的应力-应变曲线的变化特征表现一致，平台应力差异很小，同时压实应变也几乎一致，由整体变化曲线可以得出这种形状不规则度梯度组合对准静态压缩力学性能的影响很小。

图4 准静态压缩应力-应变曲线Fig.4 Quasi-static compression stress-strain curve

在不同冲击速度下模型的压缩荷载-位移曲线如图5、图6、图7、图8所示，从图中可以发现冲击端在加载一开始荷载就迅速到达峰值，之后下降进入平台段，最后进入密实阶段之后荷载急剧上升，并且随着速度的增加平台段荷载有显著的增加，但是当速度超过10 m/s之后，平台段荷载大小不再增加，速度的增加对冲击端荷载曲线几乎没有影响。而在固定端加载初期荷载为零，由于应力波的传播时间导致荷载存在明显的滞后现象，且随着速度的增加滞后越明显，固定端的平台段荷载小于冲击端并且随着速度的增加荷载差也越大，但是当速度超过10 m/s之后，速度的增加对固定端荷载-位移曲线也没有影响。由此可以判断当冲击速度由过渡模式进入冲击模式之后，速度的继续增加对荷载-位移曲线没有影响，存在临界速度。

模型分别在正、负向冲击不同冲击速度下的荷载-位移曲线对比如图7、图8所示，可以发现在固定端荷载大小和曲线变化趋势差异很小，随着速度的增加正向冲击下荷载会稍早一点急剧上升进入密实。在冲击端正、负向冲击的荷载平台段大小差异也较小，但负向冲击的荷载峰值的波动起伏都会大一些，在高速冲击下更加明显。

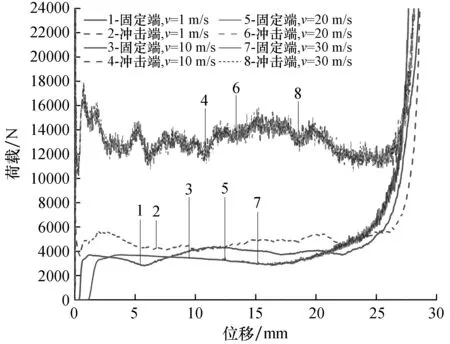
图5 A3模型不同冲击速度下的荷载-位移曲线Fig.5 Load-displacement curves of A3 model under different impact velocities

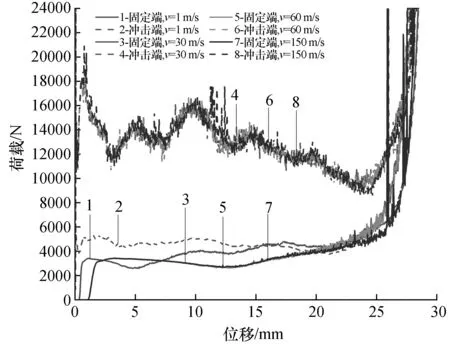
图6 A1模型不同冲击速度下的荷载-位移曲线Fig.6 Load-displacement curves of A1 model under different impact velocities

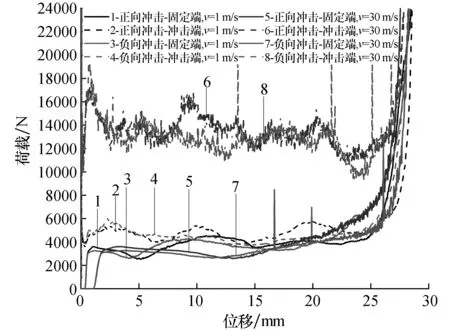
图7 A2模型正、负向冲击荷载-位移曲线对比Fig.7 Comparison of positive and negative impact load displacement curves of A2 model

四个组合模型在相同速度下的荷载-位移曲线对比如图9所示，可以看出当v=1 m/s低速加载下，各个模型的冲击端和固定端的荷载很快达到两端平衡且荷载大小相差较小。而当速度大于10 m/s，各个模型在固定端的曲线表现几乎一致，在冲击端A3模型和A4模型的差异较小，平台段相对稳定且曲线变化大致重合，但是A2模型和A1模型平台段峰值变化更大，且A1模型在密实之前存在一个明显的荷载曲线下降再上升的特征。

2.3 能量吸收

通常以模型在荷载作用下所产生的内能来表示泡沫金属吸收的绝对能量，并以此来判断它的能量吸收能力。如图10所示是A2模型在不同冲击速度下的应变-内能关系曲线，可以看出随着速度从准静态加载到高速冲击，相同应变下速度增大能量吸收会明显增加，但是存在一个临界值，就是当速度超过10 m/s之后应变-内能关系曲线全部重合，也就是说超过临界速度之后速度的增加不再改变能量吸收量。

A2模型分别在正、负向冲击下的应变-内能关系曲线如图11所示，可以看出随着速度增加，负向冲击下的能量吸收增加速率相比正向冲击缓慢一些，但是当v=30 m/s负向冲击吸收的绝对能量更大。

A4模型的正、负向冲击应变-内能关系曲线如图12所示，v=1 m/s和v=10 m/s的曲线重合，同样的当v=30 m/s负向冲击吸收的绝对能量更大。如图13所示为A2模型和A4模型负向冲击应变-内能曲线对比，当v=1 m/s两者差异很小，但在v=10 m/s和v=30 m/s冲击下，相同应变下A4模型能量吸收能力更好。

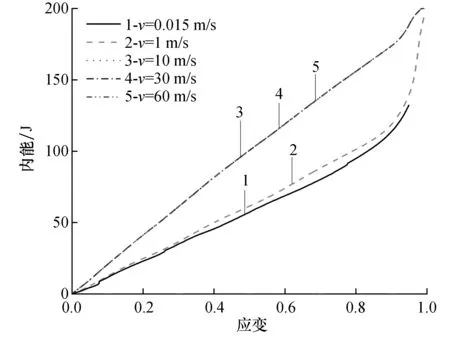
图10 A2模型不同冲击速度应变-内能关系图Fig.10 Strain-internal energy relationship of model A2 with different impact velocities

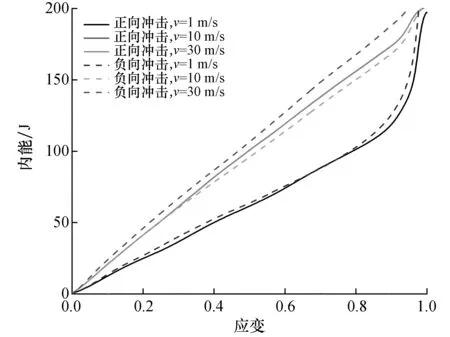
图11 A2模型正、负向冲击应变-内能关系图Fig.11 Relationship between positive and negative impact strain and internal energy of A2 model

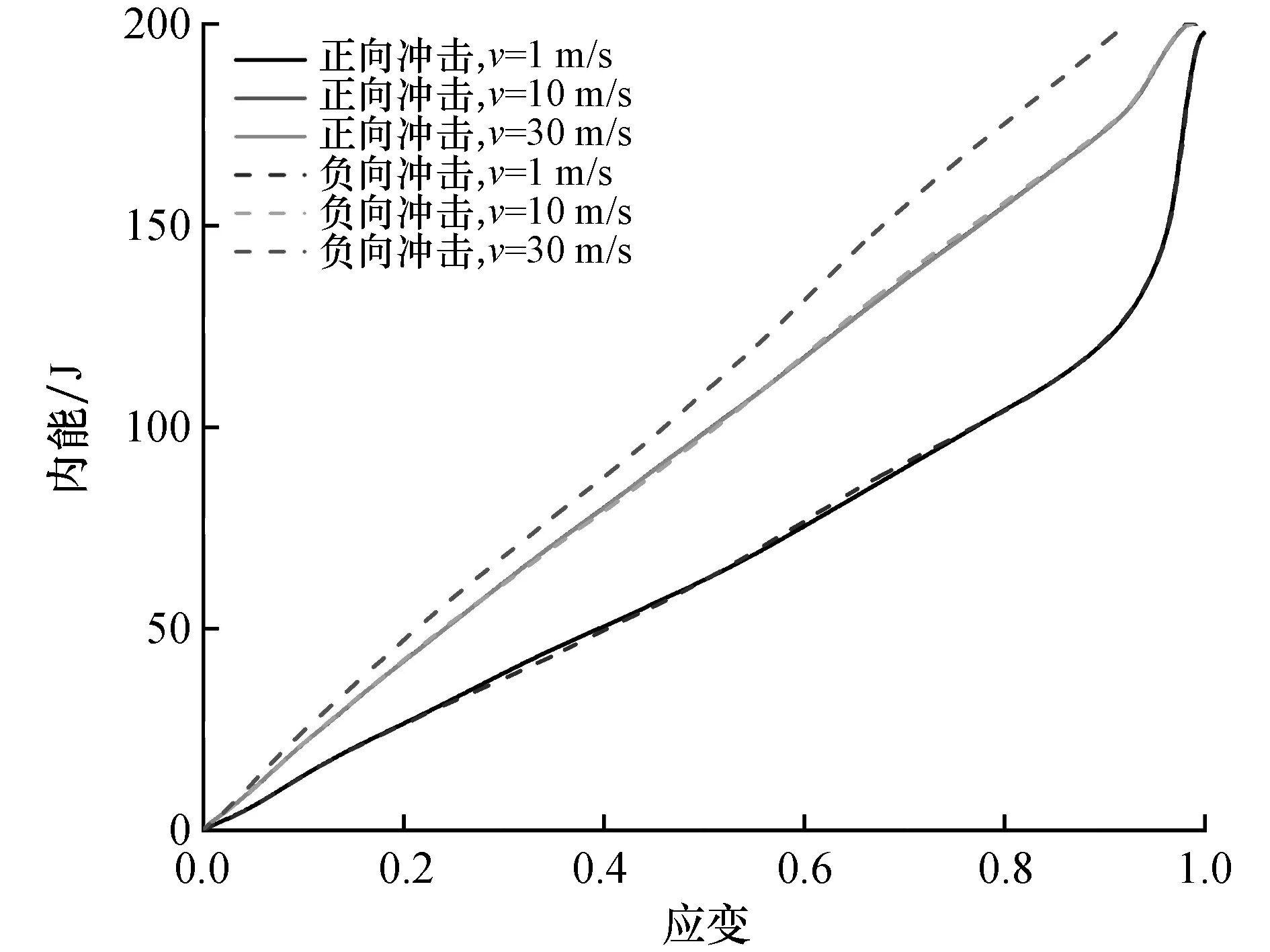
图12 A4模型正、负冲击应变-内能关系图Fig.12 The positive and negative impact straininternal energy relationship of A4 model

图13 A2和A4模型负向冲击应变-内能对比Fig.13 Negative impact strain-internal energy comparison between A2 model and A4 model

相同速度下四个组合模型的应变-内能关系曲线对比如图14(a)、(b)所示，在低速下四种组合模型的变化曲线基本重合，在高速冲击下差异也很小，只有A1模型在高应变下能量吸收略低于其它模型，所以得出在正向冲击下速度的改变对四种组合模型的能量吸收几乎没有影响。

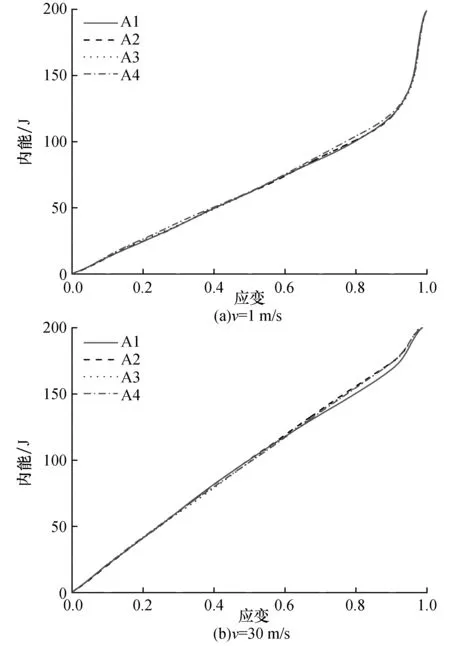
图14 相同速度下四个组合模型正向冲击的应变-内能关系曲线对比Fig.14 Comparison of strain-internal energy relation curves of four combined models under positive impact loading with the same velocity

3 结 论

1)组合梯度泡沫金属的冲击压缩随着冲击速度的增加从均匀模式到冲击模式的变化以及局部变形破坏特征表现会越明显。通过荷载-位移曲线可以发现：固定端由于应力波传播时间导致存在荷载滞后现象，随着速度增加滞后越明显，但是存在临界速度；冲击端荷载随着速度的增加而增加，也存在临界速度，超过临界速度之后速度的增加对荷载-位移曲线没有影响。

2)理想的梯度泡沫金属应具有良好的能量吸收能力和保护作用，通过应变-内能关系曲线发现在相同应变的情况下，能量吸收随着速度的增加而增加，但是存在临界速度，超过临界速度之后速度的增加不再改变能量吸收量。同时对比得出沿冲击方向形状不规则度从小到大梯度组合的模型具有更优的能量吸收能力。