基于改进型支持向量机的胶接强度预测模型
2021-03-15许明阳殷晨波
许明阳, 殷晨波, 陈 曦
(南京工业大学 车辆与工程机械研究所,江苏 南京 211816)
0 引 言
由于在役起重机械结构在长期承受工作载荷后易产生结构损伤且不易更换,胶接纤维增强复合材料补片加固钢结构得到了广泛的关注和应用。而对于胶接的复合材料补片尺寸参数而言,其长度、宽度和铺层厚度对胶接强度有很大影响,因此国内外学者进行了一系列研究。
文献[1]研究了碳纤维布加固长度对钢梁受力性能的影响;文献[2]研究了不同胶层厚度对单搭胶接接头强度的影响;文献[3]分析了补片厚度、补片形状和补片材料对模型修补效果的影响;文献[4]提出了一种运用拓扑优化技术研究复合材料结构多尺度一体化设计的方法;文献[5]采用二次规划法优化了铺层参数和层合板厚度;文献[6]利用二次方程研究了补片长度、补片厚度以及胶层弹性模量共同作用时对应力强度因子(stress intensity factor,SIF)的影响;文献[7]探讨了碳纤维布黏接长度、层数等因素对载荷传递效果的影响。
在胶接修复中,复合材料补片尺寸参数之间具有一定的关联性。从文献资料可以看出,以上研究方法虽各具优点,但多数没有考虑到参数之间的关联性,或者是基于传统方法研究了参数的关联性。
本文综合考虑了复合材料补片的长度、宽度和厚度对裂纹处应力强度因子的影响,通过有限元仿真计算出训练样本,并用应力强度因子计算公式验证其准确性;提出了基于改进的支持向量机(support vector machine,SVM)对样本进行预测和对比,进而建立最佳的基于复合材料补片尺寸参数的修复结构胶接强度预测模型。通过该模型,可以预测出经复合材料补片修复后胶接结构的强度范围,作为补片尺寸选择的参考。
1 理论分析
1.1 J积分
当前计算应力强度因子方法中,有限元法因效率高、成本低已成功运用在很多领域。本文采用ABAQUS中内置的基于J积分的方法计算修复结构裂纹处应力强度因子,J积分用于表征裂纹尖端应力、应变场的强度,是在弹塑性断裂力学中广泛采用的参数[8],其定义式为:
(1)
其中:W为应变能量密度;T为运动能量密度;σij为应力分量;uj为位移分量;δ为计算积分区域的轮廓线。
在ABAQUS中,应力强度因子与J积分的关系为:
(2)

1.2 有限元分析
胶接修复结构的钢板、胶黏剂、复合材料补片的性能参数见表1所列。
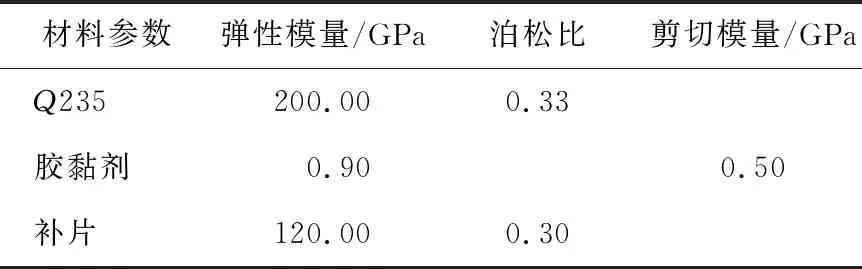
表1 胶接修复结构材料参数
在ABAQUS中建立胶接修复结构有限元模型,如图1所示。
图1中:钢板尺寸参数为200 mm×50 mm×5 mm,正中心有20 mm长的贯穿裂纹;L为补片长度;W为补片宽度;D为补片厚度;胶层厚度为1 mm。

图1 胶接修复结构有限元模型
文献[9-11]认为裂纹处SIF可以作为胶接修复结构胶接强度的判据。
本文采用ABAQUS内置的基于J积分的围道积分方法计算裂纹处的应力强度因子,设置补片的单元类型为C3D8R、胶层的单元类型为COH3D8,补片与胶层的网格大小均为1 mm。补片与胶层之间采用绑定约束、胶层与钢板之间采用绑定约束。钢板一端固定,另一端施加拉应力,大小为180 MPa。
由SIF手册查得,对于未粘贴补片的含中心裂纹钢板,其SIF计算公式为:
(3)
其中:σ为垂直于裂纹的单向外加载荷;a为裂纹半长;Y为试样形状因子修正系数。SIF手册中Y的计算公式为:
(4)
其中,b为钢板半宽。
根据(3)式计算得到图1所示模型未粘贴补片时的应力强度因子为1 109.918 MPa·mm1/2,有限元仿真计算得到的应力强度因子均值为1 133 MPa·mm1/2,相对误差仅为2.08%,说明本文所建立的有限元模型可以有效计算含中心裂纹钢板的裂纹处应力强度因子。
2 SVM预测模型建立
2.1 SVM理论
SVM适合处理非线性问题,对于小样本学习有很好的泛化能力。对于给定训练样本的分类面函数为f(x)=ωTx+b,ω、b为未知数,x为自变量。
(5)
其中:c为惩罚因子;ξi为松弛变量,ξi=max{0,1-yi(ωTxi+b)}。
引入拉格朗日因子λi,可得目标函数为:
L(ω,b,λ)=
(6)
令L(ω,b,λ)对ω、b、λ的偏导为0,可将问题转化为:
(7)
解上述问题可得最优分类面函数为:
f(x)=sgn(ωTxi+b)=
(8)
在SVM模型训练过程中,往往存在多个变量影响模型的准确度,如惩罚因子c和RBF的g参数。为了寻找最佳的模型,需要采用合适的智能优化算法在一定的区域内搜索各参数的最优组合[12]。
2.2 GA优化SVM
遗传算法(genetic algorithm,GA)具有较强的全局搜索能力,利用GA对c、g进行寻优,可以避免结果陷入局部最优。GA算法模拟遗传学机理搜索最优解,将个体算子随机选择、交叉以及变异,保证当前解集种群个体适应度值都优于迭代前,种群经过逐代演化后,末代种群达到近似最优解[13-15]。
根据寻优得到的最佳参数组c、g,即可建立GA-SVM预测模型。GA-SVM模型算法流程如图2所示。
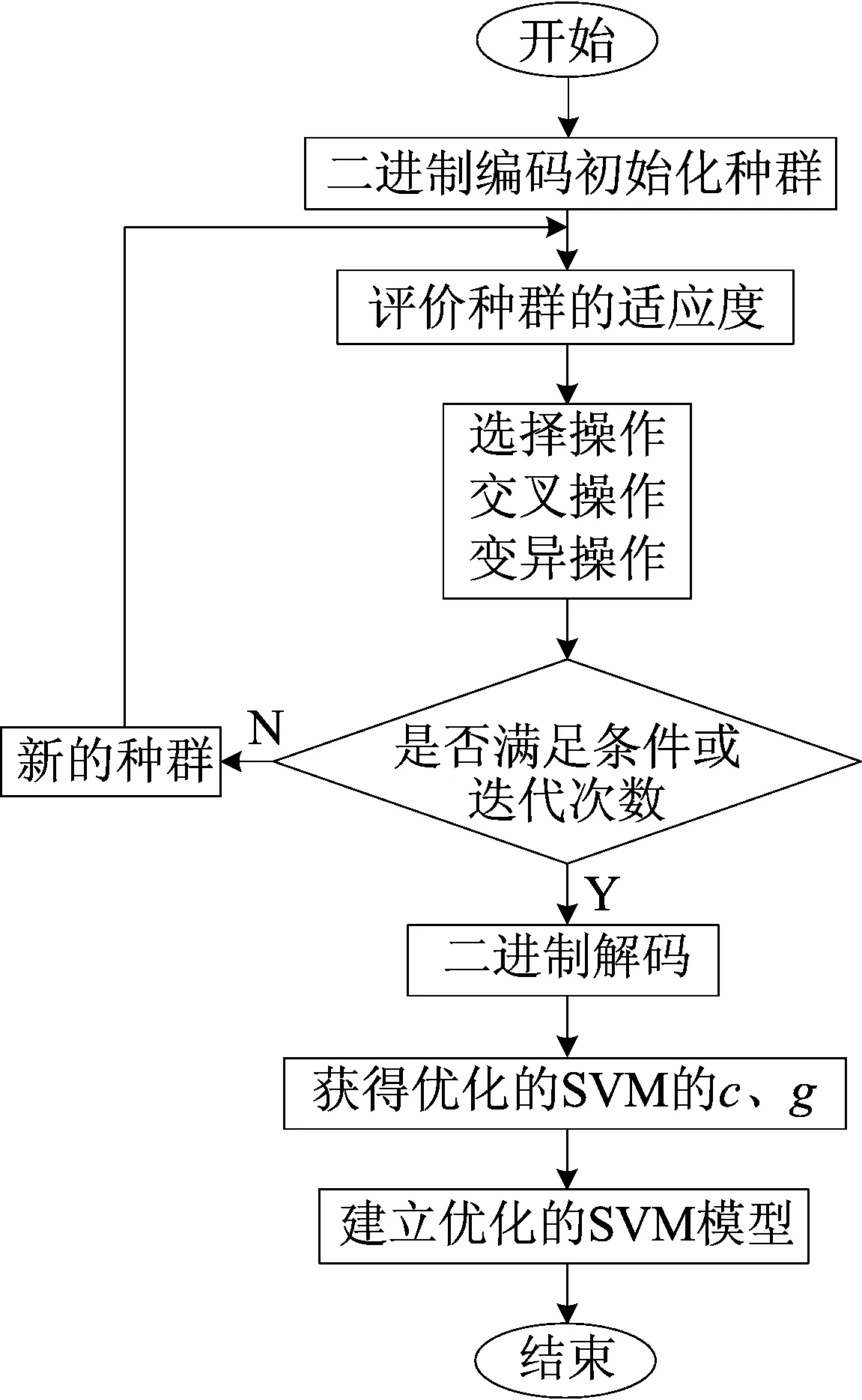
图2 GA-SVM模型算法流程
2.3 PSO优化SVM
粒子群算法(particle swarm optimization,PSO)通过初始化一群随机粒子,使每个粒子在搜索空间中单独地搜寻最优解,将其记为当前个体极值,并将个体极值与整个粒子群里的其他粒子共享,找到最优的那个个体极值作为整个粒子群的当前全局最优解,粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置[16-18]。调整公式为:
(9)
其中:pi为第i个个体的极值;pg为当前全局最优解;ω为惯性权重;c1、c2为加速常数;η1、η2为区间[0,1]内的随机数。
PSO-SVM模型的算法流程如图3所示。

图3 PSO-SVM模型算法流程
2.4 改进的粒子群算法IPSO
PSO算法容易陷入局部最优,而PSO算法的搜索能力由惯性权重ω控制[19-20]。在迭代初期ω设置得较大并缓慢地减小,能够增强初期的全局搜索能力;在迭代后期ω设置得较小,能够加快收敛速度。
本文设定ω的调整公式为:
ω=ωmax-(ωmax-ωmin)(k/maxgen)2
(10)
其中:ωmax为惯性权重的最大值;ωmin为惯性权重的最小值;k为算法当前迭代次数;maxgen为种群最大迭代次数。
一般情况下,ωmax设置为0.9,ωmin设置为0.4,本文设置maxgen为200。ω的调整曲线如图4所示。

图4 ω的调整曲线
3 仿真与分析
本文参数中,补片的长度参数L设置7个水平,分别为裂纹长度的1、2、3、4、5、6、7倍;宽度参数W设置7个水平,分别为裂纹长度的1、1.25、1.5、1.75、2、2.25、2.5倍;厚度参数D设置5个水平,分别为钢板厚度的0.1、0.2、0.3、0.4、0.5倍。以补片的长度、宽度和厚度为优化变量,输出目标为裂纹处的SIF值。
以有限元仿真结果作为训练样本,共有245组数据,部分数据见表2所列。

表2 不同尺寸参数补片胶接修复后钢板裂纹处应力强度因子
基于Matlab平台,分别采用GA-SVM、PSO-SVM、IPSO-SVM对同一245组样本集建立预测模型。
SVM模型中,c的取值区间为(0,100],g的取值区间为[0,1 000],SVM Cross Validation默认为5。
GA算法的maxgen为200,种群数量为20,终止精度为10-4;PSO算法的maxgen为200,种群数量为20,c1为1.5,c2为1.7,终止精度为10-4。
将245组样本集分成150组和95组2份,第1份供模型训练使用,第2份用于预测效果对比。3种模型预测的数据与原数据的对比如图5所示。

图5 GA-SVM、PSO-SVM和IPSO-SVM模型的预测结果
从图5可以看出:GA-SVM模型和PSO-SVM模型的整体预测效果不是很好,测试后期对峰值的预测不准确且波动较大;相比而言,IPSO-SVM模型预测结果与原数据的贴合度较高,整体效果要优于另外2种模型。
最终得到的GA-SVM模型的c=76.033 5,g=0.917 4;PSO-SVM模型的c=62.888 0,g=1.176 0;IPSO-SVM模型的c=25.278 1,g=0.841 4。
对原数据和3种模型的预测数据进行归一化处理,根据精度、均方根误差(RMSE)、平均绝对误差(MAE)来对比评价3种模型在精度和稳定性方面的优劣性。

表3 3种模型预测结果对比
从表3可以看出,IPSO-SVM模型在预测精度和稳定性方面明显优于GA-SVM模型和PSO-SVM模型,GA-SVM模型略优于PSO-SVM模型。这说明在训练样本较少时,GA算法的寻优结果要比PSO算法好,而IPSO算法可以弥补这一缺点,甚至比GA算法要更好。
4 试验与验证
应用IPSO-SVM预测模型求解目标函数裂纹处SIF最小值,所得补片尺寸参数分别为长100 mm、宽50 mm、厚2.5 mm。根据图1制得试件并进行胶接修复,拉伸试验在三思纵横UTM5305电子万能试验机上完成。
以1 mm/min加载速度对试件施加位移载荷直至试件破坏,所得未损伤钢板、损伤未修复钢板、胶接修复结构的载荷-位移曲线如图6所示。
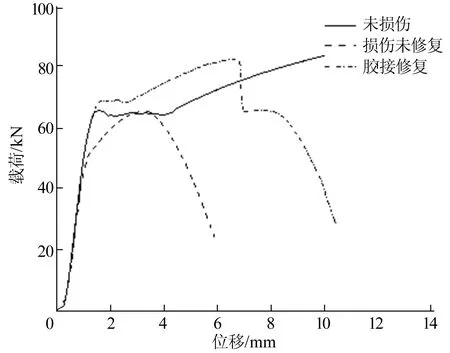
图6 拉伸试验载荷-位移曲线
由图6可以看出:损伤未修复钢板无明显屈服现象且承载能力大幅度降低;经上述尺寸补片修复后,屈服阶段位移虽未提高至与未损伤结构相同水平,但是屈服强度明显高于未损伤结构,屈服强度得到有效提高。
对比损伤未修复钢板,胶接修复结构静态承载能力提高了26%。因此,应用IPSO-SVM预测模型所得的补片尺寸参数对损伤钢板进行修复,能有效提高修复结构强度。
5 结 论
(1) 本文提出了通过SVM建立基于复合材料补片尺寸参数的修复结构胶接强度预测模型,该模型能够综合考虑补片尺寸参数之间的关联性对胶接强度的影响,为补片尺寸参数选择提供参考。
(2) 基于GA、PSO、IPSO对SVM的参数进行寻优,在训练样本较少时,GA的寻优结果要好于PSO。IPSO通过对惯性权重ω的控制,能够得到更好的寻优结果。
(3) 本文建立的IPSO-SVM模型能够准确预测修复结构的胶接强度,降低了考虑补片尺寸参数耦合时的复杂性。对于给定尺寸补片修复后的强度,不需重新建模仿真,即可通过预测模型计算得到。
(4) 应用IPSO-SVM预测模型得到的补片尺寸参数对损伤钢板进行修复,结构强度得到了有效提高。
