基于非线性和遗传变异的灰狼优化算法

王 伟, 何东之

(北京工业大学 信息学部,北京 100124)

随着科技的发展与计算领域的深入研究,生活中出现了许多复杂的优化问题。受一些生物种群活动的启发,研究人员提出了一系列群智能算法,为解决复杂的优化问题提供了新的解决方案[1]。这些算法因其具有计算方法简单、运算速度快,并且可用于解决各类优化问题而受到人们的关注,目前已提出的群智能算法包括:蚁群优化(ant colony optimization, ACO)算法[2]、粒子群优化(particle swarm optimization,PSO)算法[3]、差分进化(differential evolution,DE)算法[4]和人工蜂群(artificial bee colnony,ABC)算法[5]等。

文献[6]提出了灰狼优化(grey wolf optimization,GWO)算法。GWO模拟了灰狼的种群活动,具有与其他群智能算法相同的特点,如原理简单、算法参数少、局部搜索能力强等。但与其他群智能算法不同的是,该算法考虑了种群中的社会阶层,更大程度上模仿了生物种群所具有的特性。目前,GWO已成功应用于经济调度[7]、组合优化[8]、特征选择[9]、分类[10]、聚类[11]等领域的优化问题。此外,GWO的多目标优化[12]及其应用[13-14]也取得了一定的研究成果。

但是,基本的GWO算法除了具有许多优点外,还存在收敛速度慢、局部停滞不前的缺点。文献[15]为提高GWO算法在解决多峰值的高维度问题时的搜索精度和收敛速度, 引入了随机调整的收敛因子;文献[16]发现GWO算法对搜索空间中的坐标原点具有倾向性,提出了一种对坐标原点不敏感、可以动态调整的增强型灰狼优化算法;文献[17]提出锦标赛法、比例法和普遍抽样法等5种改进的选择策略来优化GWO算法。

针对算法容易陷入局部最优和后期收敛速度慢的问题,本文提出了一种改进的基于非线性控制因子和遗传变异的GWO算法(grey wolf optimization algorithm based on the nonlinear control factor and genetic variation,NGGWO)。首先提出一种非线性策略来替代原有的线性策略，即基于余弦函数的非线性收敛方法,提高算法的探索能力；其次将变异策略引入算法用来改进算法容易陷入局部最优的问题。

1 基本的GWO算法

在GWO算法中,提出使用α、β、δ3种最优解来模仿狼群社会中的首领,其他解被认为是ω。其中,α为适应度值最好的解决方案,其次是β,最后是δ。GWO算法通过下式来建立包围机制的数学建模,即

X(t+1)=Xp(t)-AD

(1)

D=|CXp(t)-X(t)|

(2)

其中:t为当前迭代次数;Xp(t)为猎物的位置;X(t)为灰狼个体的位置;A、C为随机系数。A、C计算公式为:

A=2ar1-a

(3)

C=2r2

(4)

其中:a在迭代过程中从2到0线性递减;r1、r2为[0,1]之间的随机数。

为实现狼群围捕机制的数学模型,算法中通过α、β、δ的位置来更新其他个体的位置,即

Dα=|C1Xα-Xi|

(5)

Dβ=|C2Xβ-Xi|

(6)

Dδ=|C3Xδ-Xi|

(7)

X1=Xα-A1Dα

(8)

X2=Xβ-A2Dβ

(9)

X3=Xδ-A3Dδ

(10)

Xi(t+1)=(X1+X2+X3)/3

(11)

其中:Xα、Xβ、Xδ分别为α、β、δ的位置;Xi为当前迭代中的第i个灰狼的位置。

2 改进的GWO算法

2.1 基于余弦函数的非线性收敛策略

群智能算法普遍存在对探索与开发的平衡问题。探索是算法在求解空间内寻找最优解的能力;开发是算法根据现有结果进一步寻优的能力。当然,每种群智能算法都有用于平衡探索与开发能力的控制因子。在GWO算法中,当|A|>1时,具有较强的探索能力;当|A|≤1时,具有较强的开发能力。因此,根据(3)式可以看出,控制因子a有着平衡探索与开发能力的作用。

在基本的GWO算法中,控制因子a随着迭代次数的增加从2线性递减到0。但是在现实问题中,若没有进行更为全面的探索,则可能使算法陷入局部最优,甚至会出现过早收敛的情况。因此,为了增加算法的探索能力,本文提出一种基于余弦的非线性策略对a进行改进,计算公式为:

a=(aini-afin)cos(kπ/2)+μ

(12)

其中:k=t/T,t为当前迭代次数,T为算法的总迭代次数;为了保证a的取值范围不变,aini、afin分别为2、0;μ∈[-1,1]为随机因子,用于改变原有的平滑曲线。

2.2 基于遗传变异的搜索策略

在基本的GWO算法中,狼群中的3个最优个体的位置确定后,它们将引领狼群进行下一次的搜索行动。但是,如果算法已经陷入局部最优,那么随着迭代次数的增加,其他个体将会向局部最优靠拢,将导致算法求得的结果是局部最优而非全局最优。因此,提出一个可以有效帮助GWO算法跳出局部最优的改进策略尤为重要。

本文为了提高算法避免局部最优的能力,在遗传算法中的变异策略的启发下,提出了通过变异策略改进GWO算法的搜索策略,采用Logistic混沌映射的思想来产生变异个体,计算公式如下:

Xi=μXi-1(1-Xi-1)

(13)

其中:Xi为混沌变量X的第i维变量;μ∈[0,4]。为保证X混沌的特性,一般将μ设定为趋近于4的值。

在根据混沌变量X得到变异个体后,将其与原个体比较,最终保留具有更优解决方案的个体。(13)式主要是根据Logistic混沌映射的特性来帮助算法产生具有不可预测的变异体。假如算法正处于局部最优的困境中,但变异体具有更优方案,这将有助于算法走出极值区域,并且可以帮助算法避免过早收敛。

2.3 NGGWO的算法流程

将非线性控制策略与新的搜索策略相结合,本文提出NGGWO,算法流程如图1所示。NGGWO算法初始化种群的时间复杂度为O(N),更新最优个体需要的迭代时间为O(T),变异次数为O(m)。因此NGGWO的时间复杂度为O(T)。

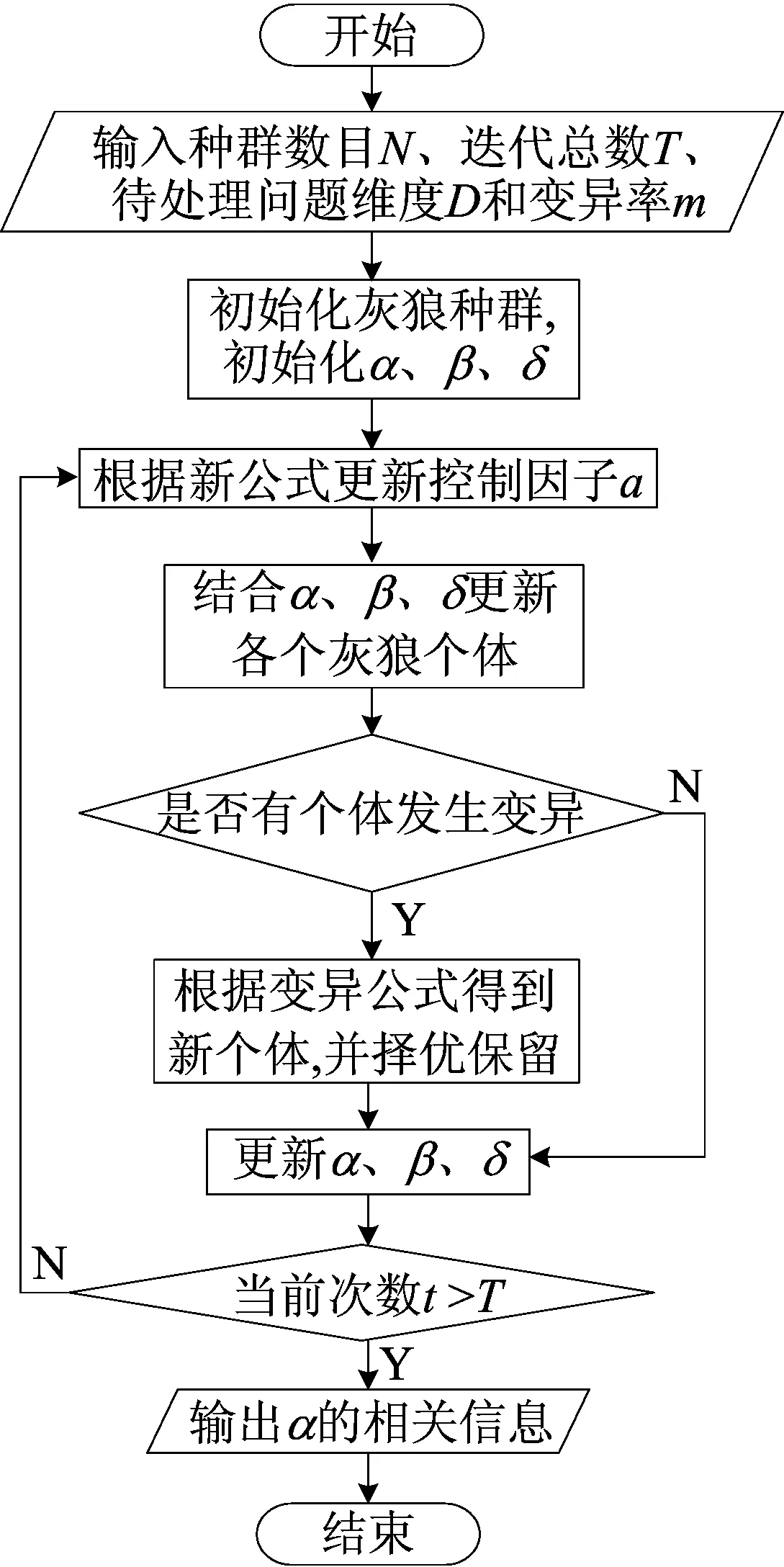
图1 NGGWO算法流程

3 数值实验与分析

3.1 测试函数与参数设置

在实验中选用的测试函数见表1所列。

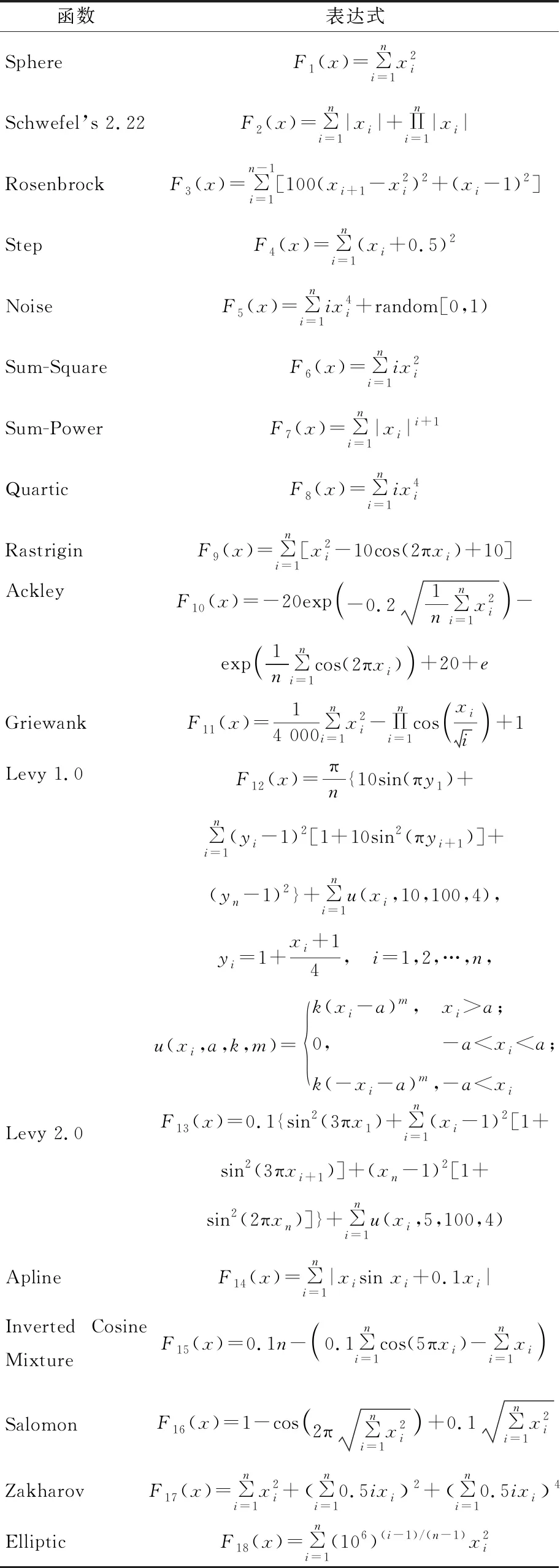
表1 测试函数

表1中各个测试函数的最优值均为0。基准测试函数主要分为单峰值(F1～F8)和多峰值(F9～F18)2组。

单峰值函数有且仅有1个最优值,不存在多个极值,适合检测算法的局部搜索能力,也就是开发能力。与此相反,多峰值函数具有多个局部最优解,便于检测算法的全局探索能力和避免局部最优的能力。为了保证实验的公平性,统一设定GWO与NGGWO的共有参数。

与实验内容相关的GWO代码均在Matlab R2014a中进行编码,所有实验都是在同一台电脑上完成,该电脑的配置为:Windows10 系统、Intel(R) Core(TM) i5-8300H CPU @ 2.30 GHz 、8.00 GB内存。

3.2 新算法与基本GWO算法的差异性分析

实验的问题维度分别设置为30、60,其他参数一致。对每个测试函数计算30次,2组测试实验结果见表2、表3所列。表2、表3中展示了计算结果的均值(Mean)和方差(Std),数据格式是Mean (Std);pW表示通过Wilcoxon检验得到的p值。

何谓小说家？毕飞宇有个有趣的说法，他说小说家就是身体倍儿棒的人，他的眼力好，旁人能看厘米，他能看毫米；旁人能听十米，他能听一里；旁人能辨五味，他能辨千滋百味。他说的是莫言，是作家那超人的感受力。不过，黄金明并不是莫言式的作家，他不是那种用身体写作的人，他是用思想写作的小说家。他没有用耳目口鼻让世界变得五光十色、五味杂陈万花筒般旋转起来，但他始终探索一种必须用宏大的思想坐标和敏锐的心智结构才能理解的先锋性十足的智性小说。

表2 30维度的实验结果

从表2可以看出,在问题维度为30时,2个算法均在函数F15上取得了最优值。此外,GWO算法在函数F12上也取得了较好的值。但是,在所有测试函数中,NGGWO算法仅在函数F12的计算结果上处于劣势。

从表3可以看出,在问题维度为60时,GWO算法仅在函数F12上取得了较好的结果。在其他测试函数上,NGGWO的计算精度优于GWO。

表3 60维度的实验结果

为了客观地检验NGGWO算法与GWO算法的性能差异,采用Wilcoxon符号秩检验方法来检验2个算法在不同维度上是否具有明显的差异,并在表2、表3的最后列出了计算结果。

从表2、表2可以看出,根据2组实验结果得到的pW值分别为0.002 3和0.001 4。2种情况的pW值都小于5%的显著性水平。这意味着NGGWO与GWO算法的性能具有显著性的差异。因此,在求解精度上,NGGWO算法优于GWO算法。

除了算法的计算精度,算法的收敛能力也是算法的性能表现。单峰值测试函数和多峰值测试函数的收敛曲线如图2、图3所示。为了更好地区分不同维度下算法的曲线,以虚线表示问题维度为30时的收敛曲线,以实线代表维度为60时的收敛曲线。

从图2可以看出,相比于GWO算法,NGGWO算法在整个算法迭代过程的早期所得到的计算精度较低,而在迭代后期曲线会呈直线趋势快速下降并且比GWO的精度更高。其主要原因是受到NGGWO算法中的非线性控制参数a的影响。在算法迭代前期,控制参数a提高了算法早期的全局探索能力,种群中的个体没有聚集在最优解的周围。在后期,NGGWO中的控制参数a慢慢变小,所有个体开始向最优解靠拢,从而加快了算法的收敛。

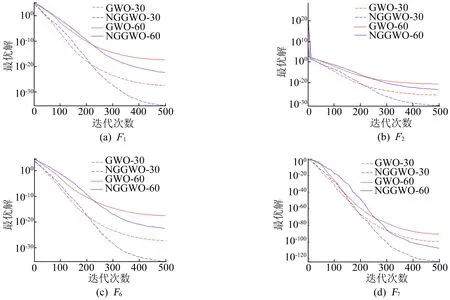
图2 NGGWO与GWO在单峰值函数上的求值曲线

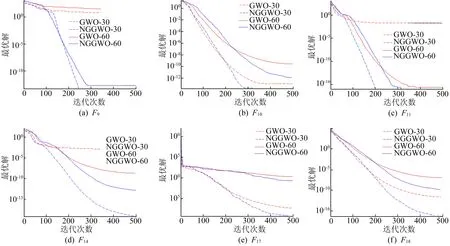
图3 NGGWO与GWO在多峰值函数上的求值曲线

从图3可以看出,多峰值测试函数在曲线收敛的情况与单峰值测试函数类似。在迭代早期,NGGWO算法的收敛效果一般没有初始的GWO效果好，在迭代后期加快了收敛,并取得较好的结果。

值得注意的是,测试函数F9、F11和F14的曲线图上可以看出,GWO的求值曲线很快趋近于水平,NGGWO算法有效地避免了算法过早收敛的情况,并取得了更精确的结果。其主要原因是NGGWO算法增加了算法对于局部停滞的改进方案,验证了文中提出的非线性控制参数策略与变异策略的有效性。

3.3 新算法与其他GWO改进算法差异性分析

为了更好地验证NGGWO算法性能,本文引入3种较新的GWO改进算法来进行算法的性能分析,分别是IGWO[15]、EGWO[16]、TGWO[17]。测试函数的问题维度设置为30,其他参数不变。此外,EGWO所特有的权重系数分别设置为ω1=0.5,ω2=0.3,ω3=0.2其中,ω1为α的权重系数;ω2、ω3分别为β、δ的权重系数。实验数据见表4所列。表4中,pF为通过Friedman检验的到的p值;R为对实验数据以秩的形式升序排序后所得到的平均排名;pB为通过Bonferroni检验得到的p值。

从表4可以看出,NGGWO算法在18个测试函数上的结果最好。在其他3个改进的算法中,相比于NGGWO算法,只有TGWO算法在测试函数F3～F5和F11～F13的实验结果上具有一定的竞争力。而IGWO与EGWO算法在所有测试函数上的实验结果都与NGGWO算法的结果相差甚多。

为了更好地检验NGGWO算法与其他算法的性能差距,本文进行了2组一对多形式的非参数比较检验,校验后的数据也见表4所列。通过Friedman检验用来比较4个算法之间是否具有显著性差异。

从表4可以看出,pF远小于5%的显著性水平。这意味着4个算法的性能完全不同。为了更好地检验它们之间的差异,采用Bonferroni检验进行事后检验,它主要是根据竞争算法之间排名来校正检验结果。

根据R的数据可以看出,NGGWO的排名高于其他3个算法,并且3组pB的值都小于5%的显著性水平,这意味着NGGWO分别与其他3个算法之间具有显著的差异。

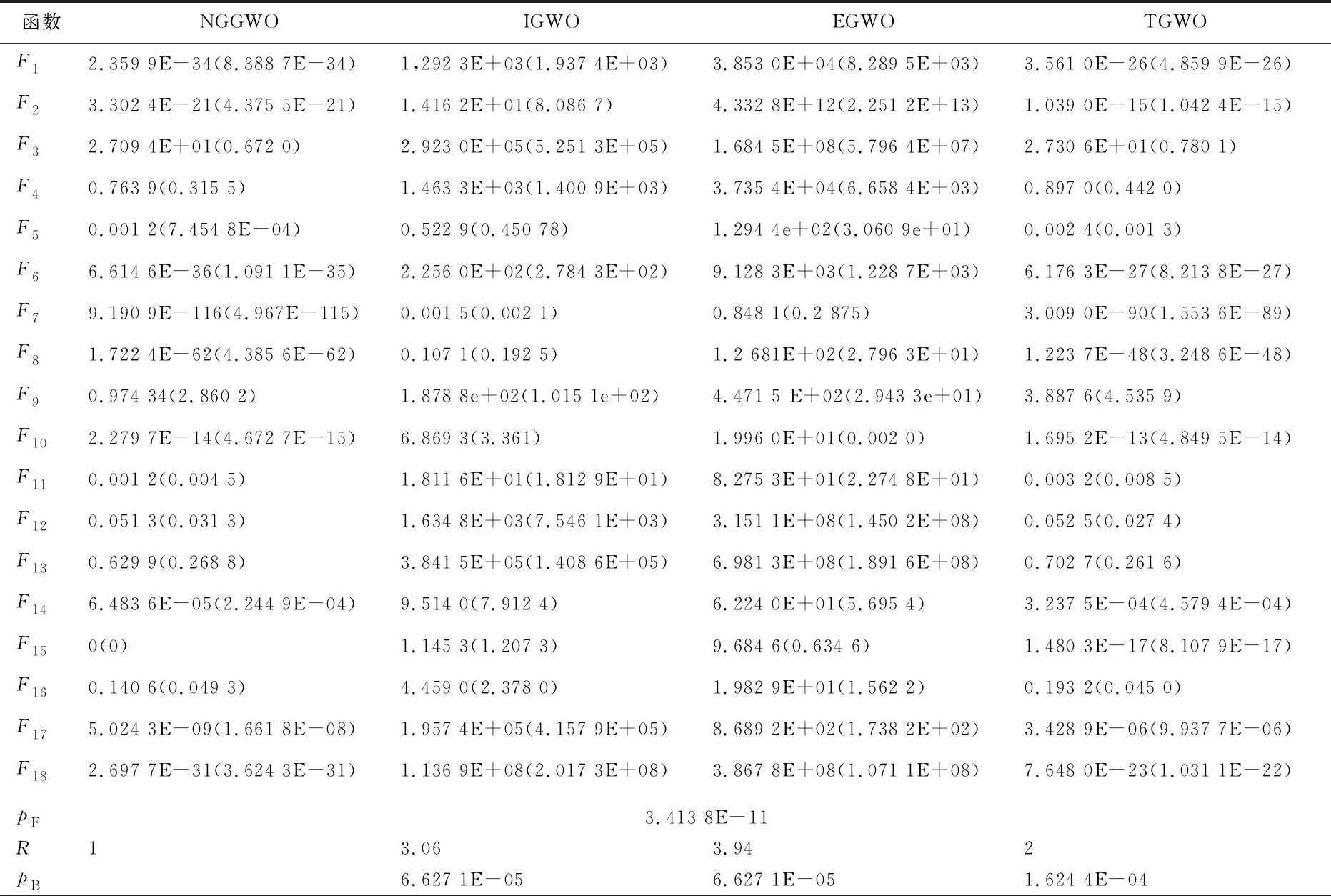
表4 4个竞争算法的实验结果

4 结 论

本文提出了一种改进的灰狼优化算法,其改进主要包括2个部分:首先提出了一种非线性控制参数a,用于平衡算法的探索和开发能力;其次提出了一种基于遗传变异的搜索策略,用于帮助算法解决局部停滞问题。通过2组实验分别将新算法与GWO、IGWO、EGWO、TGWO进行比较。第1组实验分析了NGGWO算法与GWO算法在计算精度上的差异,并通过曲线图更直观地展示了2个算法的迭代过程。第2组实验将NGGWO与IGWO、EGWO、TGWO算法进行性能差异性评估。实验结果表明:相比于GWO算法,本文提出的NGGWO算法能够更好地解决局部停滞问题,算法的计算精度更高;相比于其他3个改进的竞争算法,NGGWO算法的计算精度也具有显著的优势。