勒让德多项式的某些进一步性质

王其申

（安庆师范大学电子工程与智能制造学院，安徽安庆246133）

当把三维拉普拉斯方程在球坐标(r,θ,φ)下分离变数时，所得到的与纬度坐标θ相关的常微分方程就是连带勒让德方程（也称缔合勒让德方程）。作为其特殊情况，当问题具有轴对称性，即问题与经度方向坐标φ无关时，该方程简化为勒让德方程：

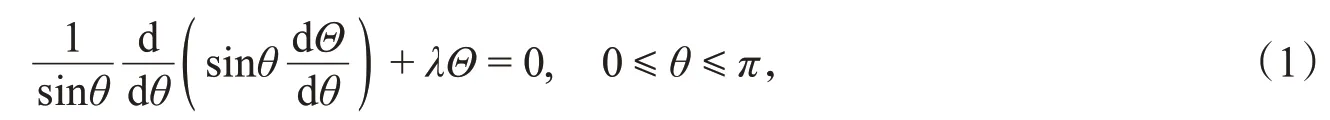
对式（1）中的自变量θ作变换x=cosθ，并记Θ(θ)=y(x)，式（1）转换为标准形式的勒让德方程：

此方程在边界条件y(±1)有界的约定下，相应的特征函数就是本文所要讨论的勒让德多项式Pn(x)(n=0,1,2,…)，它的级数表达式是

其中，[·]表示取整函数，即为方括号内数字的整数部分，下同。

勒让德多项式是物理学中一类非常重要的特殊函数。它不仅在理论物理的各个领域有着重要的应用价值，在工程问题中同样有诸多应用。因此，国内外的数学物理方法教材中都用专门的一章来介绍勒让德多项式以及更为广泛的球函数[1-6]。通常，也会介绍勒让德多项式的一系列性质，诸如它的微分和积分表达式，母函数及其递推关系，正交归一性乃至按勒让德多项式的展开定理等。

为了进一步拓展勒让德多项式的应用范围，本文作者以为，除了必须掌握数学物理方法教科书中所介绍的有关勒让德多项式的一系列重要性质外，还有必要进一步讨论其他一些重要性质。基于此，本文讨论了有关勒让德多项式的某些展开定理以及它的一阶和二阶导数的广义傅立叶展开式。

1 与勒让德多项式相关的两个展开定理

从勒让德多项式的正交归一关系出发，数学物理方法的通用教材[2-6]中都叙述了如下的展开定理。

展开定理设函数f(x)在区间[-1,1]上有连续的一阶导数和分段连续的二阶导数，则f(x)在区间[-1,1]上可以展成如下绝对且一致收敛的级数：

其中

从上面的展开定理出发，不难证明下述两个定理。

定理1设函数f(x)是区间[-1,1]上的偶函数并满足上述展开定理中的可微性条件，则f(x)可以展成如下绝对且一致收敛的仅由偶数阶勒让德多项式组成的级数：

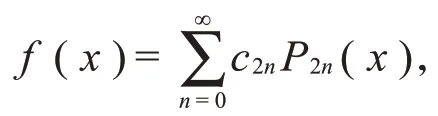
其中

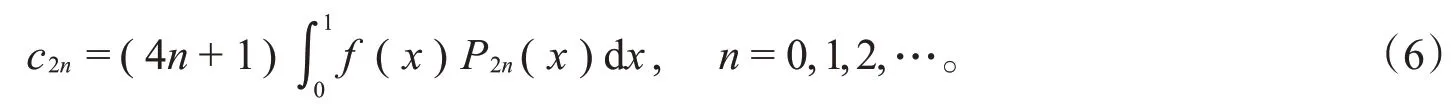
定理2设函数f(x)是区间[-1,1]上的奇函数并满足上述展开定理中的可微性条件，则f(x)可以展成如下绝对且一致收敛的仅由奇数阶勒让德多项式组成的级数：

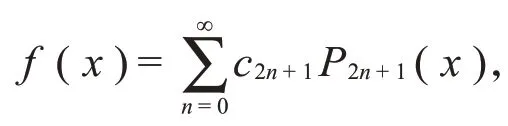
其中

以上两个定理的证明完全相似，下面仅就定理1予以证明。

证明由勒让德多项式的级数表达式（3）不难看出，奇数阶勒让德多项式仅由奇次幂函数组成，而偶数阶勒让德多项式同样仅由偶次幂函数组成，以下将其分别称为纯奇数阶多项式和纯偶数阶多项式。显然它们分别属于奇函数和偶函数。因此，当f(x)是区间[-1,1]上的偶函数时，由式（5）以及定积分的运算性质，有(x)P2n+1(x)dx=0,n=0,1,2,…；

以此带入式（4），定理1得证。

推论1纯偶数阶多项式必能展开为仅由偶数阶勒让德多项式组成的绝对且一致收敛的级数。

推论2纯奇数阶多项式必能展开为仅由奇数阶勒让德多项式组成的绝对且一致收敛的级数。

注意到纯偶（奇）数阶多项式显然是偶（奇）函数，以上推论显然成立。著名的勒让德多项式的三项递推公式(2n+1)xPn(x)=(n+1)Pn+1(x)+nPn-1(x)，（n=1,2,3,…）可以视为定理1和2的具体例子。

2 勒让德多项式的导数的两个广义傅立叶展开式

作为上面所建立的两个展开定理的应用，下面给出两个广义傅立叶展开式。

定理3成立如下的勒让德多项式的一阶导数的广义傅立叶展开式：

证明用数学归纳法证明。首先，显然有

其次，假设n=k时成立，即

现在证明n=k+1时亦成立。事实上，由勒让德多项式的另一个著名递推公式

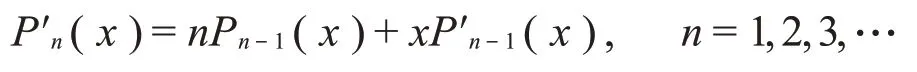
利用归纳假设，当n=k+1时，有

其中，第3个等式是利用勒让德多项式的三项递推公式，并在其中令n=k-1-2m而得到的。

特别地，P′3(x)=5P2+P0，P′4(x)=7P3+3P1，P′5(x)=9P4+5P2+P0，P′6(x)=11P5+7P3+3P1。据此，还可以给出如下递推公式：P′n(x)=(2n-1)Pn-1+P′n-2,n=1,2,3,…。这是一个以往教材中没有出现过的新的递推公式。

从定理3出发，可以进一步证明下面的定理。

定理4成立如下的勒让德多项式的二阶导数的广义傅立叶展开式：

证明对式（8）两边求导，有，应用式（8）于此式的右端，注意到当n为偶数时，[(2n-1)/2]=[(2n-2)/2]，而当n为奇数时上式和数中的最后一项实际上是零，从而可以更改求和上标，即有

交换式（10）中的两个求和号的次序并以t=m+k代替k，则有

或者换一种方法，将式（10）改写为下列矩阵乘积的形式：

注意到这个矩阵乘积中间的方阵恰好是上三角矩阵以及

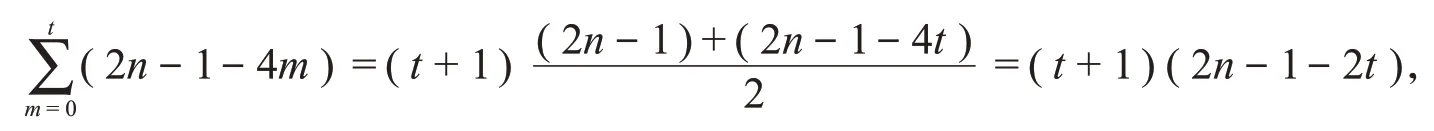
以上两种方法都证出了结论，如式（9）。

应用定理4，有

3 结束语

以上我们给出了有关按勒让德多项式展开的两个定理，以及勒让德多项式的一阶导数和二阶导数的广义傅立叶展开式。这些结果的导出过程不算困难，如果在教学中有意引导学生自行导出本文的上述结论，这对提高学生的学习兴趣，启发学生的创新和发现能力是十分有益的。