考虑不同波形影响的主应力轴连续旋转下吹填土动力特性研究*

杨爱武 杨少坤 于月鹏

(①东华大学，环境科学与工程学院，上海 201620，中国)(②天津城建大学，天津市软土特性与工程环境重点实验室，天津 300384，中国)

0 引 言

近年来，随着海洋资源的开发利用，栈桥、装卸码头、海上钻井平台等越来越多的海洋建筑物在近海软黏土地基上修建(刘晓磊等，2020)，这些设施修建之后软土地基必定长期遭受不同波形的循环荷载作用，使得海床土体应变发展、孔压累积特性及抗液化强度均发生显著变化，从而引起地基的压缩、破坏和失稳现象(Bea et al.，1983)。目前国内外众多学者对软黏土进行了不同波形作用下的动力特性试验研究，并取得了诸多成果。Thiers et al.(1968)分别在正弦波和三角波条件下对旧金山湾黏土施加不同应力幅值的循环荷载，结果发现正弦波作用下土体强度比三角波作用下土体强度低10%左右；Behzadi et al.(1996)利用矩形波对澳大利亚黏土进行了一系列室内循环三轴试验，得到了可以预测路基土在指定应力水平下永久变形的模型；蒋军等(2001)分别采用正弦波、三角波、锯齿波以及矩形波对黏性土开展了长期循环荷载作用下的室内固结试验，结果表明不同波形循环荷载作用下的结果相差无几；戴文亭等(2008)研究了循环荷载作用下加载波形、应力幅值、围压、频率及加荷周数对黏性土动力变形影响，发现加载波形对土体塑性变形影响最小，且不同波形对土体变形的影响取决于荷载最大值时历时的长短；张启辉等(2007)对上海软土进行了动力三轴试验，利用损伤观点探讨了其动力条件下的应力-应变发展规律，研究指出三角形波相比正弦波更容易导致土体破坏；曹勇等(2013)通过采用正弦波、三角波和方波分析了海积原状软黏土在不同循环荷载波形下的应变特性，当循环应力幅值小于临界应力时，加载波形对土体变形影响并不明显，当幅值大于临界应力后，不同波形下的土体变形量均显著增加，且方形波荷载作用下的变形量达到最大；雷华阳等(2009)基于滨海新区结构性软土的大量动三轴试验发现，振动波型对土体动应力-应变关系影响不大，但是最大动弹性模量Edmax和最大动剪切模量Gdmax的数值相差可达2.5倍左右；毕雪梅(2013)采用正弦波对天津滨海吹填软土开展循环荷载作用下的室内动三轴试验，分析了固结围压、频率、波形等因素对动应力-应变关系的影响以及孔压、动弹性模量、阻尼比等随循环振次的变化规律；杨爱武等(2017)以结构性软黏土作为研究对象，分别对其施加正弦波和方波两种波形循环荷载作用，发现同条件下方波累积变形量总是大于正弦波，而正弦波作用下孔压值总是大于方波；郭飞等(2018)对比分析结构性软土在不同循环荷载波形下的刚度软化规律，得到了能够综合考虑加载波形和应力幅值的软化指数经验公式。

不难发现，目前关于循环荷载作用下不同波形对软黏土动力特性的研究多采用振动三轴仪和动扭剪仪，此时土体单元的主应力方向只能发生90°突变。然而波浪荷载作为一种典型的循环荷载，其作用于海床地基土体中的主要特征之一是：轴向应力偏差与施加剪应力耦合形成的偏应力幅值并不发生变化，而土体主应力轴方向在循环加载过程中却发生180°的连续变化(Madsen，1978)，这与常规动三轴试验或循环扭剪试验中土单元体的应力状态有着明显区别，因而并不能真实反应出波浪荷载作用下海床土体的实际受力情况。因此，深入了解地基土在复杂应力条件下的动力特性对于海洋构筑物的稳定性评价有着重要的现实意义。Matsui et al.(1992)针对波浪循环荷载作用下软黏土的强度弱化、应力-应变及孔压特性进行了研究；Wang et al.(2019)讨论了主应力轴连续旋转对饱和软黏土孔压、模量软化及应变发展的影响；栾茂田等(2009)通过饱和黏土的耦合循环剪切试验，对波浪荷载下地基土单元体的复杂应力路径进行模拟，分析了主应力轴连续旋转条件下土体的应力-应变特性和动力参数变化规律；Shen et al.(2017)探讨了波浪荷载作用下主应力轴突变和连续旋转对软黏土强度和孔压变化的影响；严佳佳等(2014)在主应力轴旋转条件下研究了剪切应力对杭州软黏土应变发展和孔压累积的影响；杨彦豪等(2015)进行等向固结条件下的主应力轴旋转试验，分析了波浪荷载作用下软黏土在不同频率及循环应力比条件下的应变发展、模量衰减等动力特性；曹洋(2013)利用空心圆柱扭剪仪模拟波浪荷载下海床地基土体单元的实际受力条件，对饱和软黏土动力特性进行了研究。

综上所述，以往研究学者大多采用正弦波对波浪荷载的加载形式进行模拟，但研究发现波浪荷载的实际波形是三角波及正弦波的合成波(Kim，1978)(图1分别为正弦波、三角波及真实波浪波形示意图)。而室内试验中难以模拟这种不规则的循环荷载，基于此，为了探索实际情况下波浪荷载作用对海洋构筑物地基的影响，本文利用GCTS动态空心圆柱扭剪仪，在主应力轴连续旋转条件下分别采用正弦波和三角波来研究天津滨海吹填土应变发展、动强度及孔压累积特性，并对比分析两种波形对吹填土动力特性的影响，以期为相关工程建设提供理论支撑。

图1 不同荷载波形示意图Fig.1 Diagram of different waveformsa.正弦波；b.三角波；c.波浪荷载真实波形

1 试验内容及方法

1.1 试验仪器及土样应力状态

试验仪器采用美国GCTS公司研发的动态空心圆柱扭剪仪，它可独立控制内围压Pi、外围压Po、轴力W及扭矩T对空心圆柱试样进行加载。该仪器在具备普通静、动三轴仪和扭剪仪功能的同时，还可以研究多种荷载波形、频率以及复杂应力状态下的主应力旋转等问题。在加载条件下，空心圆柱试样受力及单元体应力状态如图2所示。

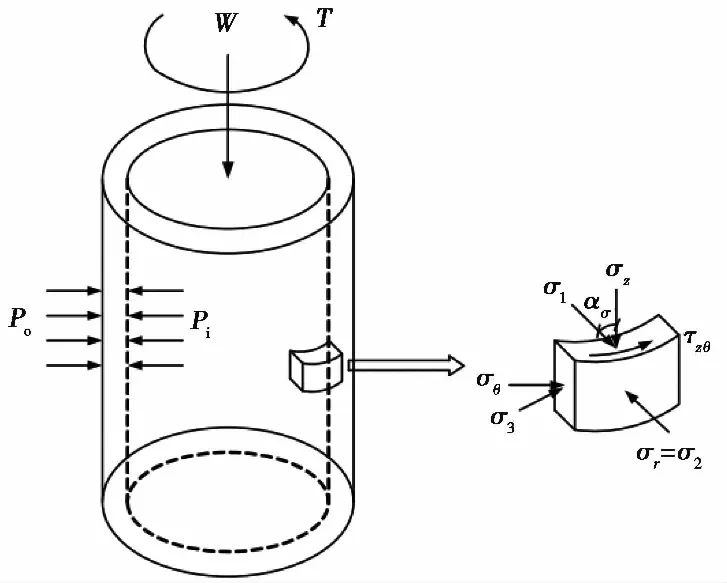
图2 空心圆柱薄壁单元体应力状态Fig.2 Stress state on an element of hollow cylinder sample

分析图2中试样单元体应力状态，其有4个独立的应力分量，即扭矩T产生扭剪应力τzθ，内围压Pi、外围压Po产生环向正应力σθ和径向正应力σr，轴力W及内、外围压产生轴向正应力σz。一般情况下，有σr=σ2。

通过空心圆柱扭剪仪同时、独立地对试样施加轴力和扭矩变载，加载过程中控制应力参数：平均主应力p、大主应力方向角α、中主应力系数b以及剪应力q来实现土体动主应力轴发生180°的连续旋转。应力坐标体系选择为：

(1)

室内循环剪切试验中，土样在固结完成后达到一个最终稳定的应力状态，称之为初始固结应力状态。对各初始固结主应力可由下式计算：

(2)

(3)

(4)

此外，综合考虑轴向变形与剪切变形的耦合作用，采用广义剪应变γg对试验结果进行分析：

(5)

式中：ε1、ε2、ε3分别为大主应变、中主应变、小主应变。

1.2 土样制备及加载方案

试验用土均为原状软黏土，取自天津滨海新区临港工业区某吹填场地，取样深度集中在3～8m，吹填土主要物性指标如表1所示。

表1 吹填土物理力学性质指标Table 1 Physical and mechanical properties of soft dredged fill

试验采用空心圆柱试样，其尺寸为内径×外径×高度=50mm×100mm×200mm。采用孔压系数B值来检测土样饱和程度，由于吹填土试样体积较大、渗透系数较低，规定当B值达到0.95以上时认为土样达到饱和要求。首先将通过专用制样设备制好的原状土样进行真空饱和，再装入GCTS空心扭剪系统的压力室中进行反压饱和，根据对天津吹填土空心圆柱试样反压饱和的研究(王腾辉等，2012)，将围压和反压的压差恒定控制在15kPa将不至于对试样造成破坏，本次试验共分5级加压，从初始围压10kPa开始依次加压，压力增幅均设为50kPa，每级围压和反压施加完毕后实时记录孔压变化，待孔压接近反压时施加下一级围压和反压，最后一级围压施加完毕时测得孔压系数B值符合规定。试样饱和完成后施加100kPa围压(p′)对其进行三向等压条件下的固结，参考《土工试验方法标准》(中华人民共和国行业标准编写组，2019)，规定固结过程中试样1h内排水量不超过0.1cm3即视为达到固结稳定标准，固结完成后开展不排水条件下主应力轴连续旋转的应力路径试验。

加载过程中，控制扭矩T与轴力W的相位角相差90°，且保持循环轴向应力幅值的一半σd/2与循环剪应力幅值τd相等，则能够实现循环大主应力方向角αd在0°～180°之间连续变化，为了控制剪切过程中的试样的应力路径分别为圆形和菱形，分别采用加载频率0.1Hz正弦波和三角波来模拟波浪荷载真实应力状态，从而完成对不同波形和主应力轴方向耦合变化的复杂应力路径加载。通过改变循环剪应力幅值τd大小，分别研究主应力轴连续旋转情况下不同循环剪应力幅值及波形对吹填土动力特性影响。试验发现，当τd低于5kPa时，随着振动次数的不断增加，试样广义剪应变发展曲线几乎与X轴重合，实际中并不具备研究意义；而当τd=20kPa、αd在0°～180°之间连续变化时试样破坏过快，因此设计循环剪应力幅值τd在5～20kPa范围内取值。试验停止标准为广义剪应变达到10%或振动次数达3000次，具体加载方案如表2所示。

表2 试验加载方案Table 2 Test loading scheme

2 试验结果与分析

2.1 广义剪应变发展特性

不同波形作用下广义剪应变随循环振动次数的变化如图3所示。

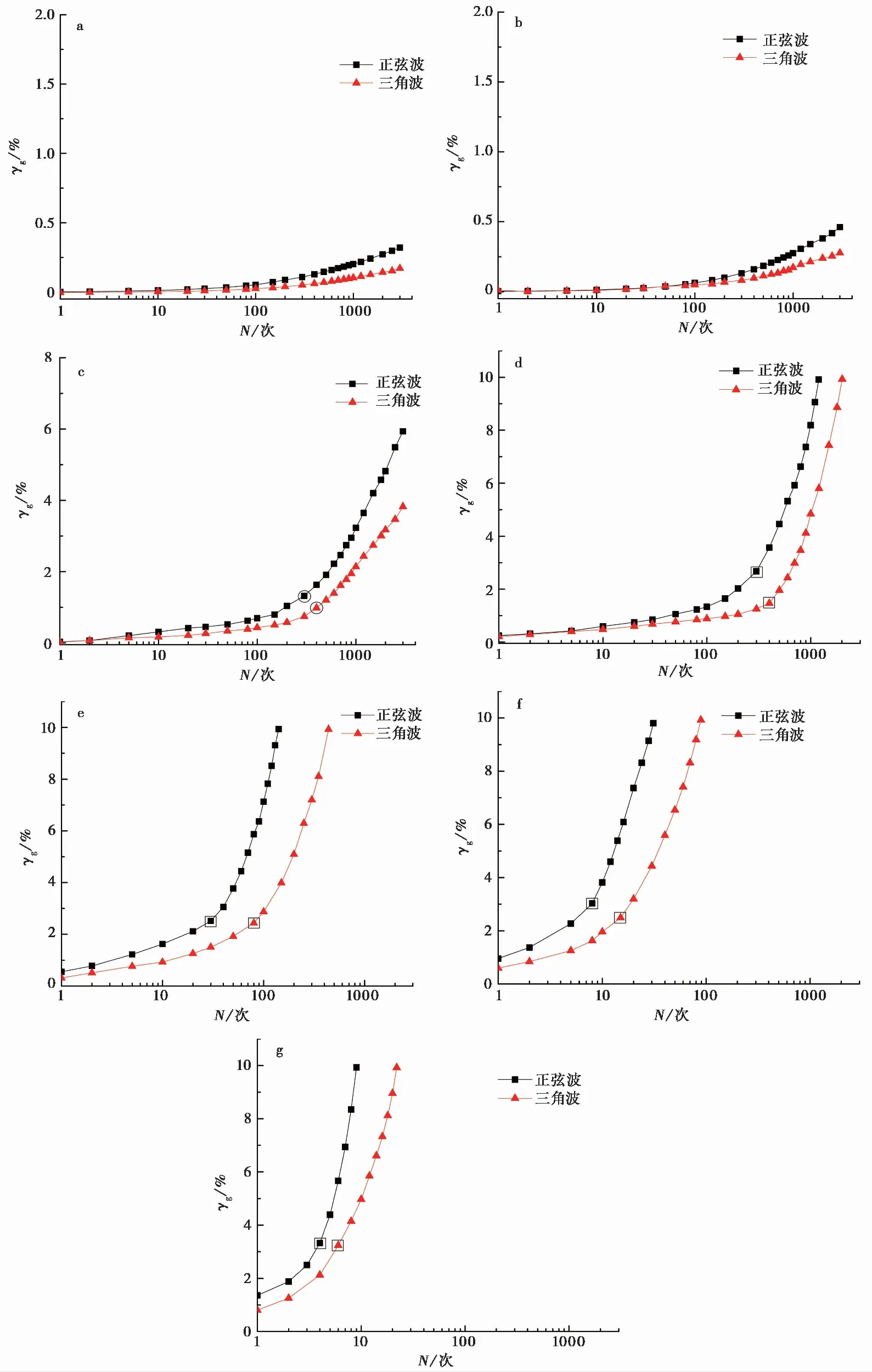
图3 不同波形下广义剪应变随循环振次变化曲线Fig.3 Variation curves of generalized shear strain with cyclic number under different waveformsa.τd=5kPa；b.τd=7.5kPa；c.τd=10kPa；d.τd=12kPa；e.τd=14kPa；f.τd=16kPa；g.τd=18kPa

由图3可见，加载波形对吹填土广义剪应变有一定的影响。当循环剪应力幅值为5kPa和7.5kPa时，两种波形作用下的γg-N关系曲线差别并不明显，土体广义剪应变变化很小且增长缓慢，此时波形对土体变形影响较小；随着循环剪应力幅值的增加，循环荷载作用初期广义剪应变发展缓慢，当循环荷载达到一定振次后，土样变形急剧增大直至破坏，且相同循环剪应力幅值下，正弦波广义剪应变的发展速率大于三角波，同等振次下正弦波对应的广义剪应变始终大于三角波。

由图3还可以看出，当循环剪应力幅值不大于7.5kPa时，两种波形作用下的广义剪应变变化幅度较小，而当剪应力幅值为10kPa时，随着振次的增加，两种波形下土体变形均显著增大并出现明显的转折点(图3c中圆圈所示)，表明土体的临界循环剪应力介于7.5kPa到10kPa之间，且不因外部荷载作用形式而改变其大小；当循环剪应力幅值超过10kPa时，两种波形下所施加的循环剪应力越大，广义剪应变在整个动载过程增长都较快，土体达到一定广义剪应变(γg=10%)所需振动次数越少。这是因为吹填土体具有结构性，当施加循环剪应力小于土体临界循环剪应力时，土颗粒在循环荷载作用下有一定程度的挤压密实，内部联结作用加强，粒间接触更加紧密，此时土体变形主要表现为土颗粒的压密变形，土体微结构较为完整，基本没有破坏或遭到轻度破坏；随着循环剪应力的增大，当超出土体临界循环剪应力不多时(τd=10kPa)，在振动的开始阶段，土颗粒将发生滑移、旋转及换位，从而产生一定的变形量，并出现明显的应变转折点，随振次的增加土体将逐渐达到破坏；当循环应力继续增大至远大于临界循环剪应力时，土颗粒间联结将发生不同水平的错动或断裂，打破了颗粒间原有的结构状态，土体内部连接更加疏松，部分脱离接触，稳定性大幅减弱，土体变形急剧增大。

2.2 动强度特性

土的动强度通常被定义为在特定循环振动次数下产生某一指定破坏应变或发生液化状态时对应的循环剪应力幅值(李作勤，1994)。对于竖向和扭转耦合剪切的主应力轴循环旋转试验，应同时考虑两者的共同作用，因此采用式(6)给出的最大动剪应力幅值作为一般情况下的动强度：

(6)

动强度试验中的破坏标准有：孔压标准、屈服标准和应变标准。由于黏土的滞后性(刘忠玉等，2019)，在主应力轴循环旋转试验中发现土体孔隙水压力无法达到有效固结围压，故将孔压作为土体的破坏标准无法实现。以往关于黏土的研究中，通常采用应变达到某一特定值作为土体的破坏标准，但是其破坏标准的选择并不统一。因此，为了探讨不同破坏标准对土体动强度的影响，本文以广义剪应变发展过程中出现转折点处的应变值εtp(图3中方框所示)、广义剪应变达到5%及10%作为土体破坏的取值标准，3种破坏标准下对应的循环振次为破坏振次，不同破坏标准下土体动强度与破坏振次Nf之间的关系曲线如图4所示。

图4 不同破坏标准下动强度与破坏振次间关系Fig.4 Relationship between dynamic strength and failure cyclic number under different damage standarda.正弦波；b.三角波

由图4可以看出，动强度大小与破坏标准的取值有关，相同破坏振次下，破坏标准取值越大，动强度值越大。不同破坏标准下的动强度都随振次增加呈减小趋势，当破坏振次较小时，3种破坏标准下动强度值差别较大，且达到相同剪应力幅值所需振动次数随破坏标准取值的增加而增加；随着破坏振次的增大，3种破坏标准下的动强度最终趋于同一数值，此时不同的破坏标准对土体动强度影响不大。因此，设计时为了安全起见，宜按变形发展中出现转折点处对应的应变值作为破坏标准。

为了更直观地反映不同波形对动强度作用的影响，图5给出了两种波形下动强度与破坏振次间的关系曲线。通过对比可知，不同波形循环剪切荷载作用下的动强度值亦有所差别。相同循环剪应力幅值下，正弦波比三角波对应破坏振次要少，即当循环振次相同时，三角波对应土体破坏时动强度大于正弦波，说明正弦波在主应力轴循环旋转效应下与三角波相比更容易导致土体破坏。随着破坏振次的增大，土体破坏时对应的动强度逐渐趋于一致，这说明当破坏振次较大时，两种波形对土体动强度的影响减小。产生以上现象可从能量角度进行解释：由于相同循环应力幅值和振动频率条件下正弦波能量较大，导致其对吹填土内部结构损害程度高，所以正弦波作用下吹填土的动强度值要小于三角波的作用情况。随着破坏振次的增大，两种波形作用下，土体内部结构均不断进行调整，当土体结构彻底破坏并最终接近重塑状态时，此时达到一种新的平衡状态，动强度最终趋于相同数值，同时由于相同条件下三角波能量小于正弦波，故当趋于相同数值时，三角波荷载作用下所需破坏振次要明显大于正弦波。

图5 不同波形下动强度与破坏振次间关系Fig.5 Relationship between dynamic strength and failure cyclic number under different waveformsa.γg=εtp；b.γg=5%；c.γg=10%

表3对比了3种破坏标准下两种荷载波形分别作用时吹填土动强度试验结果，结合图5和表3发现，不同破坏标准下，随着循环剪应力的减小，两种波形对应的动强度与破坏振次间关系曲线变化趋势均逐渐变缓，最终将趋于一致。在破坏振次Nf=10～500范围内，破坏标准取εtp时正弦波作用下动强度比三角波降低约2.1%～6.7%，破坏标准取5%时降低约5.5%～8.6%，破坏标准取10%时降低约6.9%～9.5%，说明随着破坏标准取值的增大，不同振动波形对土体动强度的影响愈加显著。

表3 两种荷载波形作用下动强度结果对比Table 3 Comparison of dynamic strength under two loading waveforms

对表3数据进行分析，发现不同波形荷载作用下的动强度τf与破坏振次Nf之间具有良好的对应关系，可采用式(7)进行表述：

τf=a+blnNf+c(lnNf)2

(7)

对应不同破坏标准及波形下的各参数a、b、c值如表4所示，R2表示拟合度。

表4 不同破坏标准及波形下各参数值Table 4 Parameters under different damage standard and waveforms

由表4可以看出，R2均在0.98以上，说明采用此公式能较好地描述两者的变化关系，为了进一步验证动强度与破坏振次间关系式的准确性及适用性，分别取两种波形作用下广义剪应变达8%时对应的动强度值与利用式(7)所得计算结果进行比较，如图6所示。

图6 γg=8%时试验与预测结果对比Fig.6 Comparison of test results and prediction curves under γg=8%

由图6可以发现，试验结果与计算结果吻合度较好，说明上述公式可以反映不同破坏标准及波形下动强度随破坏振次的变化情况。

2.3 孔压累积特性

循环荷载作用下砂质或粉质土体孔压会发生动态变化，并按照一定发展趋势出现液化现象，从而导致土体失稳破坏；就黏土而言，孔压的产生和发展与砂土或粉土并不相同(郭进雪等，2018；张艳美等，2018)。图7为不同波形作用下孔隙水压力随循环振次的发展曲线。

图7 不同波形下孔隙水压力随循环振次发展曲线Fig.7 The development curves of pore water pressure with cyclic number under different waveformsa.正弦波；b.三角波

由图7可见，随着循环荷载振动次数的增加，孔压逐渐累积，且正弦波作用下土体孔压增长速率大于三角波。当施加循环剪应力小于土体临界循环剪应力时，加载初期孔压随循环振次的增加而增加，随后孔压增长速率开始降低，并渐趋稳定，进入动态平衡状态；未达到破坏应变时，随循环应力幅值的增大，孔压持续发展；当循环剪应力幅值远大于临界循环剪应力时，土体很快达到破坏状态，孔压急剧增长。产生这些现象的原因与前述广义剪应变发展机理相一致，即施加循环剪应力较小时，变形主要表现为颗粒的压密变形，土体内部结构破坏小，同时空隙连通性较好，相应的超孔隙水压力逐渐上升；随着循环剪应力的增大，土体结构性破坏加大，原本应由土颗粒通过其接触点传递的压力传给孔隙水进行承担，引起孔压的显著增加，土体变形快速增长直至破坏；此外，由于相同条件下正弦波能量高于三角波，正弦波对土体结构破坏程度大，因此随循环振次的增加，正弦波作用下土体孔压发展速率高于三角波。

由图7还可以发现，相同循环振次下孔压随循环剪应力幅值的增大而增大，且剪应力幅值越大，孔压增长速率越快；然而达到破坏应变时孔压发展迅速，其幅值却相对较小。这是因为循环荷载作用下黏土孔压滞后于应变的发展，当循环剪应力幅值较大时，加载初期孔压增长速度较快，测量到的孔压值与实际值存在一定误差，图中值只代表孔隙水压力的变化趋势，并不是实际孔压值，这也进一步说明采用有效应力法分析循环荷载作用下饱和黏土地基稳定性时，只考虑加荷时孔压产生的影响是不妥的，滞后的孔压会引起地基土体的压缩和破坏。

3 考虑主应力轴旋转效应的探讨

在前人研究的基础上，通过与毕雪梅(2013)采用GCTS空心圆柱扭剪仪对天津滨海吹填土进行的循环三轴试验(无主应力轴旋转)进行对比，可以发现如下规律：

(1)在其他条件相同的情况下，主应力轴循环旋转对土体动应变与循环振次关系具有显著影响。当土单元主应力方向只发生90°突变时，振动次数3000次时的动应变幅值不到2%，土体塑性应变并不明显，孔隙水压力发展比较缓慢，要在较高的振动次数下才能达到其动应力临界值；而当主应力轴方向发生180°的连续旋转时，土体在较低的应力水平(τd=7.5～10kPa)下便达到其临界循环剪应力，施加循环剪应力超出其临界值后，土体广义剪应变快速发展直至破坏。可见波浪荷载引发的主应力轴旋转路径下吹填土的临界应力水平明显不同于三轴应力路径，考虑主应力轴循环旋转效应后，随着循环应力幅值的不断增加，土体逐渐转为大变形破坏，因此建议在工程实际中针对土体所承受的复杂加载形式，采取相应路径下的临界应力水平展开设计，以保证相关工程建设的安全和稳定。

(2)同等条件下，毕雪梅在循环三轴试验中按等效正弦波施加应力幅值分别为15kPa、20kPa、40kPa时，以动应变拐点处的取值作为破坏标准，其在特定循环振次N=50、100、200、500次下的临界动应力值分别为38.92kPa、32.53kPa、26.63kPa、23.01kPa，与本文主应力轴旋转下的转折点破坏标准相比较，对应动强度分别提高了2.85倍、2.51倍、2.17倍、1.96倍。由此可见，动三轴应力路径下吹填土动强度远比主应力轴连续旋转路径下高出很多，进一步说明了在工程实际中考虑主应力轴旋转影响从而使设计偏于安全的重要性。

4 结 论

(1)天津滨海吹填土存在一个临界循环剪应力值，且不因外部荷载作用形式而改变。施加循环剪应力小于临界循环剪应力时，土体广义剪应变变化幅度很小且增长缓慢，波形对土体变形影响较小；循环剪应力超过临界循环剪应力后，土体在较少的振动次数下便产生较大的变形，且相同循环剪应力幅值下，正弦波广义剪应变的发展速率大于三角波，同等振次下正弦波对应的广义剪应变始终大于三角波。

(2)不同破坏标准下的动强度均随破坏振次增加呈减小趋势，最终将趋于同一数值，相同振次下破坏标准取值越大，动强度值越大。同等循环剪应力幅值下正弦波比三角波对应破坏振次要少，且随破坏标准取值的增大，正弦波作用下动强度比三角波作用降低明显。基于试验数据，建立了考虑不同破坏标准时两种波形作用下动强度与破坏振次间关系式。

(3)随循环荷载振动次数的增加，土体孔压逐渐累积，同等条件下正弦波作用时孔压增长速率大于三角波。循环剪应力幅值越大，孔压增长速率越快，达到破坏应变时其孔压迅速累积，但由于黏性土孔压滞后效应明显，整个试验过程中其幅值却相对较小。

(4)考虑主应力轴循环旋转效应后，土体临界应力水平明显降低，且主应力轴连续旋转路径下的吹填土动强度远比动三轴应力路径下低很多。