初始孔压非均布双层地基一维固结性状分析

江唯伟，张军辉

（1．广东省公路勘察规划设计院股份有限公司，广州 510030；2．长沙理工大学公路工程教育部重点实验室，长沙 410004）

初始孔压非均布双层地基一维固结性状分析

江唯伟1，张军辉2

（1．广东省公路勘察规划设计院股份有限公司，广州 510030；2．长沙理工大学公路工程教育部重点实验室，长沙 410004）

根据双层地基固结理论，推导出瞬时加载、单面排水、初始孔压非均布的一维固结解答。给出了双层地基不同工况对应的简化初始孔压分布图，以便实际运用。通过编制的计算程序，分析了不同初始孔压分布对双层地基一维固结性状的影响。结合硬壳层地基固结的计算实例，分析了硬壳层应力扩散效应对固结曲线影响。

初始孔压分布；混合法；双层地基；一维固结；应力扩散；硬壳层

自H．Gray［1］给出了瞬时加荷情况下双层地基一维固结解析解以来，双层地基固结理论在考虑任意加载方式［2］、材料非线性［3－5］、应力历史［6］、半透水边界条件［7］方面得到了长足的发展，但很少考虑初始孔压分布对双层地基固结的影响。Terzaghi and Peck［8］就不同初始孔压分布形式对固结度的影响进行了分析，但只是针对单层地基。李飞［9］对单层地基不同初始孔压分布的一维固结性状进行了分析。谢康和给出了初始孔压沿深度任意分布的双层地基一维解答［10］，但没有对其固结性状进行分析。本文根据双层地基固结理论，导出了瞬时加载、单面排水、考虑初始孔压非均布的固结公式，对其固结性状进行了分析，给出了实际运用条件。并结合计算实例，说明了硬壳层应力扩散效应对固结曲线的影响。

1 初始孔压线性分布的双层地基固结求解

对应于瞬时加载单面排水条件下的单层地基数学模型可用下式表示。

控制方程：

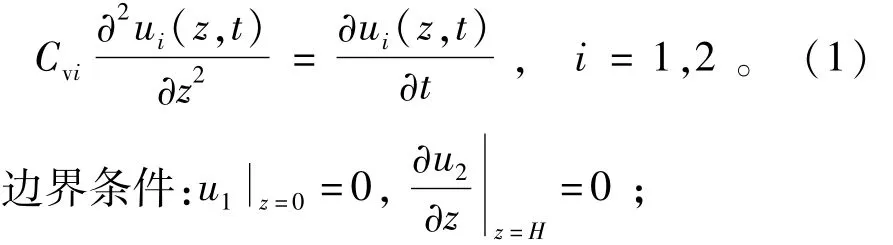
初始条件：

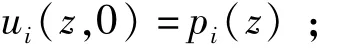
层间连续条件：

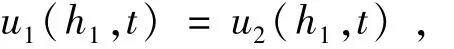
各参数含义如下：ui（z，t）为第i层土的超孔隙水压力；pi（z），Cvi，kvi，Esi，msi分别为第i层土的初始超孔隙水压力、固结系数、渗透系数、压缩模量、体积压缩系数γw为水的重度；h1，h2分别为第1，2层土的厚度，H＝h1＋h2。根据变量分离法可得考虑初始孔压分布的解析解如下［10］：

其中：λm为超越方程（λm）tg（μcλm）＝1的正根，m＝1，2，…。

定义参数：

将初始超孔隙水压力的分布假定为双线性，即假设：

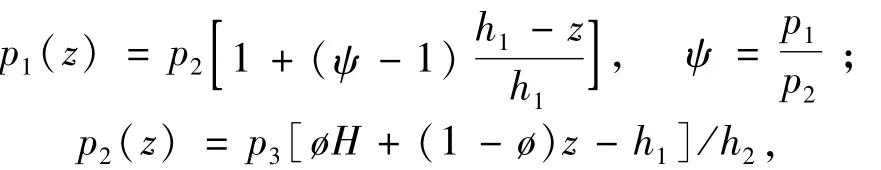
p1，p2，p3分别为z＝0，z＝h1，z＝h1＋h2时的初始孔压力，分布见图1。

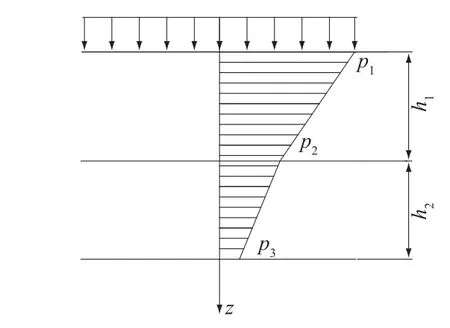
图1 初始孔压计算模型Fig．1 Computation model of the distribution of initial pore water pressure

将p1（z），p2（z）代入Cm中得

其中：

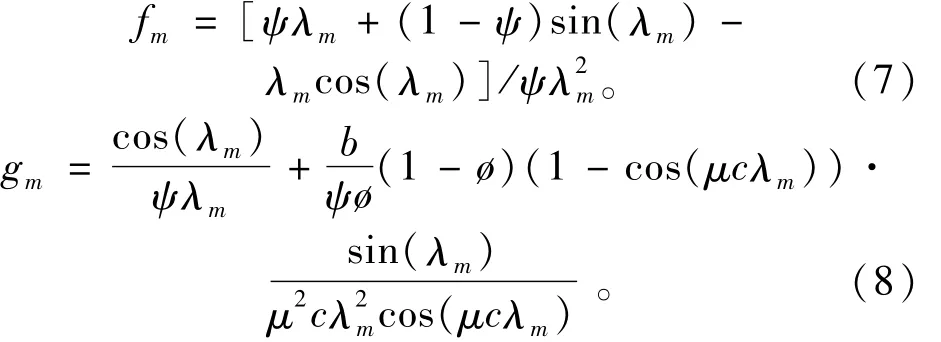
当φ＝ø＝1时，Cm退化到双层地基初始孔压为常数的情况。

即

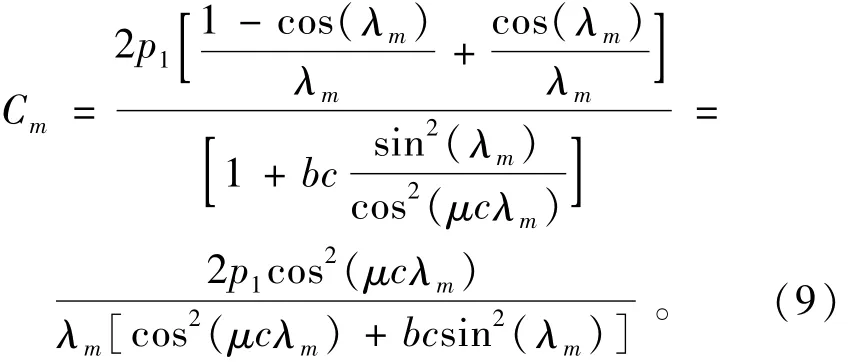
令：

则按沉降定义固结度有

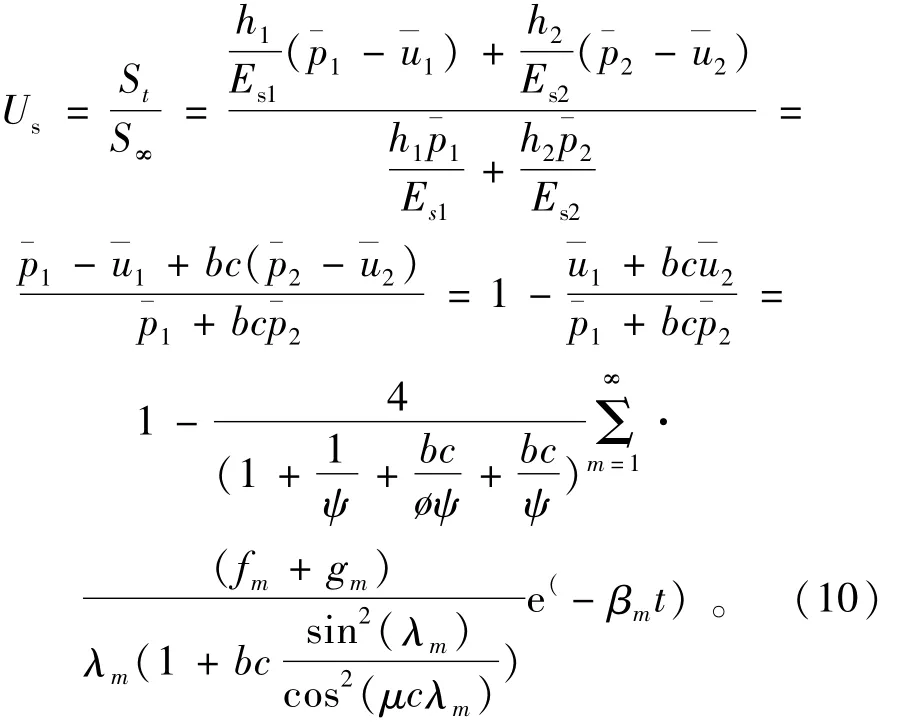
从式（10）中可看出，在a，b，c一定情况下，Us的大小只与ψ，ø的大小有关，即与初始孔压比p1∶p2∶p3的大小有关。

2 程序验证

在求解超越方程时，先通过f（a）×f（b）＜0寻找有根区间［a b］，再通过将割线法、二分法和二次反插法相结合的混合法［11］，求得有根区间对应的正根。笔者编制可以考虑初始应力分布为双线性分布的计算程序DLSS。程序验证时首先退化为初始孔压均匀分布双层地基固结问题，然后退化为初始孔压线性分布单层地基固结问题，计算结果与已有解答完全一致，说明编制程序的可靠性。

2．1 退化为初始孔压均匀分布双层地基固结

当ψ＝ø＝1，即可退化到初始孔压均匀分布双层地基固结情况，取a＝10，b＝1，c＝1，时间参数Tv＝（Cv1／H2）t，即退化到文献［12］中图3对应的双层地基固结曲线，如图2所示的曲线1。

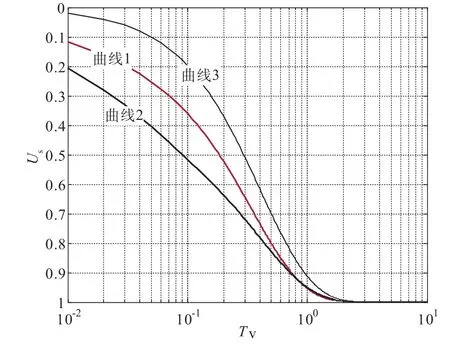
图2 模型验证的固结曲线Fig．2 Consolidation curves ofmodel validation

2．2 退化为初始孔压线性分布单层地基固结

取a＝b＝c＝1时，即可退化到考虑初始孔压线性分布的单层地基固结问题，取p1∶p2∶p3＝100∶50．005∶0．01，即可退化为单层地基初始孔压沿深度减小的三角形分布，取p1∶p2∶p3＝0∶100∶200，即可退化为单层地基初始孔压沿深度增加的三角形分布，2条曲线分别见图2所示的曲线2与曲线3，与文献［13］中图4－29的曲线一致。

3 初始孔压分布的双层地基固结性状分析

3．1 典型初始孔压分布对固结曲线的影响

在工程实际中，不同工况将产生不同的初始孔压分布。图3为5种工况对应的简化初始孔压分布图，此时压缩土层为双层地基。5种不同的工况如下：

（1）基础底面积很大而压缩土层较薄的情况；

（2）无限宽广的填土层，由于自重应力而产生固结的情况；

（3）基础底面积较小，在压缩土层地面的附加应力已接近于零的情况；

（4）在地基自重作用下尚未固结就在上面修筑建筑物基础的情况；

（5）基础底面积较小，在压缩土层地面的附加应力还不接近于零的情况。

图3 初始孔压分布简化图Fig．3 Simplified distribution of initial pore water pressure

可知当初始孔压沿深度减小时，固结速率在前中期要快于初始孔压为常数的情况；当初始孔压沿深度增加时，固结速率在前中期要慢于初始孔压为常数的情况。

3．2 下层地基初始孔压变化对固结曲线的影响

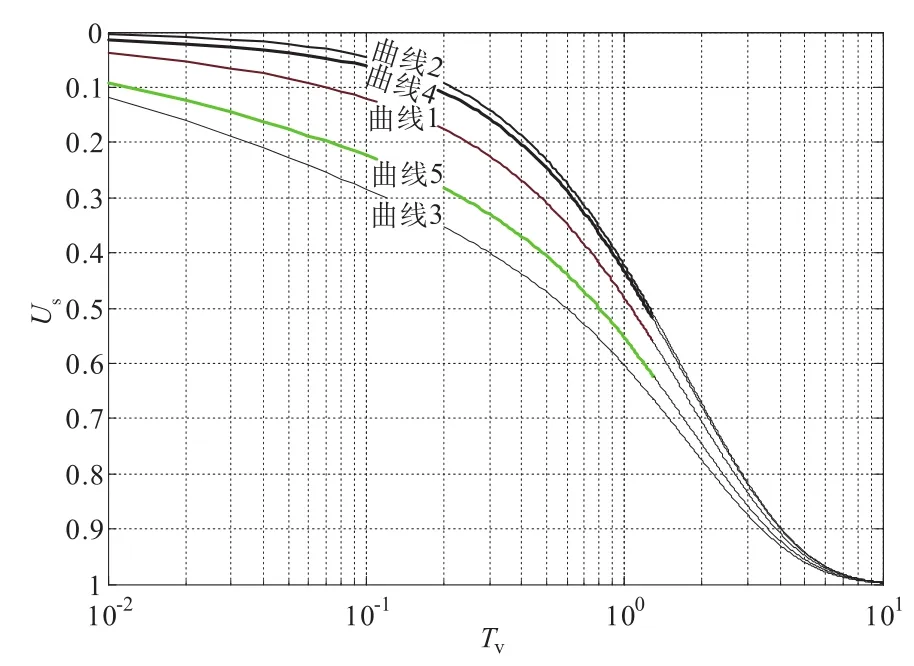
图4 典型初始孔压分布对应的固结曲线Fig．4 Consolidation curves of typical distribution of initial pore water pressure

图5 下层地基不同初始孔压的固结曲线Fig．5 Consolidation curves of different initial pore water pressures in the lower ground

由图5可得到下层地基初始孔压变化对固结曲线的影响为：随着p2∶p3的增大，在前中期固结的越快，最大差值可达到22%（b＝5时），19%（b＝0．5时），但在后期与初始孔压不变的情况趋于一致。当p2∶p3趋于无穷大时，固结曲线即为该种情况的下限。

3．3 上层地基初始孔压变化对固结曲线的影响

由图6可得到上层地基初始孔压变化对固结曲线的影响为：随着的增大，固结的前中期将比不考虑初始孔压的情况要偏快，最大差值可达到12%（b＝5时），10%（b＝0．5时），但在后期将趋于一致。当趋于无穷大时，固结曲线即为该种情况的下限。

通过对比图5与图6可知，图5中曲线1—8的变化幅度均大于图6的，可知单面排水条件下，下层地基初始孔压变化对固结曲线的影响要比上层的大。

图6 上层地基不同初始孔压的固结曲线Fig．6 Consolidation curves of different initial pore water pressures in the upper ground

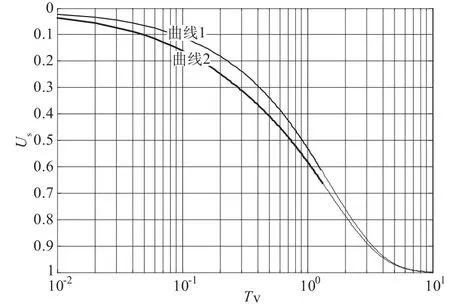
图7 固结曲线的对比Fig．7 Com parison of consolidation curves

4 计算实例

硬壳层软土地基上承受条形均布荷载大小为P1＝100 kPa，荷载分布宽度为L＝10 m，硬壳层厚度为h1＝4 m，软土层计算深度为h2＝30 m，硬壳层与软土层压缩模量比为b＝6，软土层与硬壳层渗透系数比为a＝0．5。荷载加载方式假设为瞬时加载，地基顶面排水，底面不透水，采用工况5下的初始孔压分布进行计算。

4．1 附加应力计算

通过应力扩散角法得知［14］，当h1／L＝0．4，b＝6时，应力扩散角为φ＝27．8°。所以层间处荷载分布宽度L1＝L＋2h1tanφ＝14．2 m，有p2＝p1L／L1＝70．4 kPa。

通过文献［15］中应力扩散角法提供的方法求解软土层层底的附加应力为p3＝15．3 kPa。因此有p1∶p2∶p3＝100∶70．4∶15．3。

4．2 固结度计算

通过编制程序计算得Us－T v，其中T v＝（Cv1／H2）t，固结度曲线见图7，其中曲线1是初始孔压均匀分布的情况，曲线2为初始孔压实际分布的情况，可见固结曲线在前中期是有差异的，考虑初始孔压实际分布的土体要比孔压均匀分布的土体在前中期固结的更快一些。对于此算例，最大固结度差值达到8%左右。

4．3 硬壳层应力扩散效应对固结曲线的影响

已有研究表明［15］，影响硬壳层应力扩散效应的主要因素为厚宽比（硬壳层的厚度与荷载分布宽度的比值）和模量比（硬壳层与软土层压缩模量的比值）。模量比越大，应力扩散越显著；厚宽比越大，应力扩散越明显。结合以上分析可知，硬壳层应力扩散作用越强，竖向附加应力沿深度减小越大，在固结前、中期与初始孔压均布情况相比固结的越快。

5 结 论

本文通过理论推导，编制相应计算程序，定性地分析了初始孔压分布对固结曲线的影响，并结合计算实例，得到了以下结论：

（1）在固结参数a，b，c一定的情况下，固结曲线只与初始孔压比p1∶p2∶p3的大小有关。

（2）考虑初始孔压分布的双层地基固结性状比单层的复杂得多，但总体趋势与单层相似。当初始孔压沿深度减小时，固结速率在前中期要快于初始孔压均布的情况。孔压减小越多，固结过程越快，固结曲线在后期趋于一致；当初始孔压沿深度增加时，固结速率在前中期要慢于初始孔压均布的情况。孔压增加越多，固结过程越慢，固结曲线在后期趋于一致。

（3）对于单面排水的情况，下层地基的初始孔压变化对固结曲线的影响较上层的大。

（4）硬壳层应力扩散作用越强，竖向附加应力沿深度减小越大，在固结前、中期与初始孔压均布情况相比固结的越快。

（5）在实际应用中，对涉及到以上5种工况的初始孔压分布可简化为图3所示的情况。

［1］ GRAY H．Simultaneous Consolidation of Contiguous Layers of Unlike Compressible Soils［J］．ASCE Transactions，1945，110：1327－1356．

［2］ 谢康和．变荷载下任意层地基一维固结理论［J］．岩土工程学报，1995，17（5）：80－85．（XIE Kang-he．Onedimensional Consolidation Theory of the Arbitrary Layer Foundation Under Variable Load［J］．Chinese Journal of Geotechnical Engineering，1995，17（5）：80－85．（in Chinese））

［3］ 王宏志，陈仁朋，周万欢，等．双层地基一维非线性固结的DQM解［J］．水利学报，2004，（4）：8－14．（WANG Hong-zhi，CHEN Ren-peng，ZHOUWan-huan，et al．Computation of 1-D Nonlinear Consolidation in Double-layer Foundation by Using Differential Quadrature Method［J］．Journal of Hydraulic Engineering，2004，（4）：8－14．（in Chinese））

［4］ 袁坚敏，谢康和．双层地基一维非线性固结性状分析［J］．科技通报，2005，21（4）：471－475．（YUAN Jianmin，XIE Kang-he．Analysis of1-D Nonlinear Consolidation Behavior of Double-Layered Soils［J］．Bulletin of Science and Technology，2005，21（4）：471－475．（in Chinese））

［5］ 刘祚秋，富明慧，周翠英．变荷载下任意层地基一维非线性固结的数值分析［J］．中山大学学报（自然科学版），2007，46（5）：1－4．（LIU Zuo-qiu，FU Ming-hui，ZHOU Cui-ying．Numerical Analysis of One Dimensional Nonlinear Consolidation of Layered Foundation under Time Dependent Loading［J］．Acta Scientiarum Naturalium Universitatis Sunyatseni，2007，46（5）：1－4．（in Chinese））

［6］ 温介邦，谢康和，胡安峰．双层超固结软黏土地基一维非线性固结分析［J］．水利学报，2007，（2）：226－232．（WEN Jie-bang，XIE Kang-he，HU An-feng．Analysis on One-dimensional Nonlinear Double-layered Over-consolidation Soil Foundation［J］．Journal of Hydraulic Engineering，2007，（2）：226－232．（in Chinese））

［7］ 胡凌华，谢康和．成层地基半透水边界一维固结分析［J］．科技通报，2005，21（3）：321－326．（HU Ling-hua，XIE Kang-he．Analysis on One Dimensional Consolidation Behavior of Layered Soil with Partial Drainage Boundaries［J］．Bulletin of Science and Technology，2005，21（3）：321－326．（in Chinese））

［8］ TERZAGHIK，PECK R B．Soil Mechanics in Engineering Practice（Third Edition）［M］．New York：John Wiley＆Sons，1967．

［9］ 李 飞，葛爱兵．初始孔压分布对地基土一维固结性状影响研究［J］．路基工程，2007，（6）：1－5．（LI Fei，GE Ai-bing．Research on One Dimensional Consolidation Behavior of Foundation Soil by Distribution of Initial Pore Water pressure［J］．Subgrade Engineering，2007，（6）：1－5．（in Chinese））

［10］谢康和．双层地基一维固结理论与应用［J］．岩土工程学报，1994，16（5）：24－35．（XIE Kang-he．One-dimensional Consolidation Theory and Application of the Double-Layered Ground［J］．Chinese Journal of Geotechnical Engineering，1994，16（5）：24－35．（in Chinese））

［11］PRESSW H，FLANNERY B P，TEUKOLSKY S A，et al．Numerical Recipes in C-The Art of Scientific Computing（Second Edition）［M］．New York：Cambridge University Press，1992．

［12］谢康和．双层地基固结实用计算理论与曲线（一）［J］．地基处理，1993，4（4）：1－14．（XIE Kang-he．Consolidation Calculation Theory and Curve of Double-Layered Ground（1）［J］．Foundation Treatment，1993，4（4）：1－14．（in Chinese））

［13］陈仲颐，周景星，王洪谨．土力学［M］．北京：清华大学出版社，1992：145－148．（CHEN Zhong-yi，ZHOU Jingxing，WANG Hong-jin．Soil Mechanics［M］．Beijing：Tsinghua University Press，1992：145－148．（in Chinese））

［14］王晓谋．硬壳层软土地基竖向附加应力扩散的数值分析［J］．长安大学学报，2007，27（3）：37－41．（WANG Xiao-mou．Numerical Analysis on the Vertical Additional Stress Diffusion of Hard Shell Layer Soft Soil Foundation［J］．Journal of Chang’an University，2007，27（3）：37－41．（in Chinese））

［15］梁永辉．上覆硬壳层软土地基的工程特性试验研究及数值分析［D］．上海：同济大学，2007，（3）：21－22．（LIANG Yong-hui．Model Tests and Numerical Study on Engineering Properties of Soft Subsoil with Upper Crust［D］．Shanghai：Tongji University，2007，（3）：21－22．（in Chinese） ）

（编辑：王 慰）

One Dimensional Consolidation Behavior of Double-Layered Ground w ith Non-uniform Distribution of Initial Pore W ater Pressure

JIANGWei-wei1，ZHANG Jun-hui2
（1．Guangdong Highway Design Institute Co．Ltd．，Guangzhou 510030，China；2．Key Laboratory of Highway Engineering of Ministry of Education，Changsha University of Science and Technology，Changsha 410004，China）

According to the consolidation theory of double-layered ground，a solution is given to the problem of onedimensional consolidation in consideration of instant load，singleside drain and non-uniform distribution of initial pore water pressure．The simplified diagram of initial porewater pressure distribution under differentworking conditions is given for engineering practice．The influence of initial pore water pressure distribution on one-dimensional consolidation behavior of double-layered ground is analyzed through computer program．The impact of stress spreading in dry crust on the consolidation curves is illustrated by calculating examples．

distribution of initial pore water pressure；hybrid method；double-layered ground；one-dimensional consolidation；stress spreading；dry crust

TU43

A

1001－5485（2013）09－0080－05

10．3969／j．issn．1001－5485．2013．09．016

2013，30（09）：80－84

2012－10－07；

2012－10－11

江唯伟（1985－），男，湖北荆州人，硕士，工程师，主要从事路基路面及地基处理方面的研究，（电话）15099957531（电子信箱）327410253＠qq．com。