基于离散颗粒模型的岩体结构面动-静态刚度系数对比的数值模拟研究*

周 剑 王彦兵 张路青 金永军 涂新斌

(①北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124，中国)(②中国科学院地质与地球物理研究所，中国科学院页岩气与地质工程重点实验室，北京 100029，中国)(③国网经济技术研究院有限公司，北京 102209，中国)

0 引 言

与岩石块体相比，岩体中往往具有一组或多组节理、层理、片理或其他类型结构面(谷德振，1979；Brady et al.，2013)。岩体中结构面的发育程度、规模大小、组合形式等是控制岩体稳定性的重要因素(Goodman，1976)，同时还影响着岩体的渗透性(Pyrak-Nolte et al.，1990)。结构面的力学特性是诸多地质工程高效开发及安全运营的关键因素，包括高陡岩质边坡工程(Wu et al.，2017;Hu et al.，2018)、深部硬岩隧道工程(Feng et al.，2018)、二氧化碳地质封存(Iding et al.，2009)、非常规油气水力压裂开采(Maxwell et al.，2002)、增强型地热系统建设(Zimmermann et al.，2010)等。Goodman et al.(1968)较早地对岩体结构面变形行为进行了研究，并提出节理单元模型，之后许多学者在此基础上提出各种改进的节理单元(Brady et al.，2013)。岩体工程的定量计算中引入节理单元后实现了岩石块体之间的非连续性变形计算，计算结果与工程实践符合更好。在岩体力学计算分析中，结构面的法向刚度kn与切向刚度ks是必要的力学参数，计算分析的精度和可靠程度与这两个参数密不可分。因此，获取较为准确的结构面法向、切向刚度显得十分重要。王芝银等(2011)提出基于岩体三轴压缩试验的节理力学参数确定方法：通过节理岩体常规三轴试验测得的应力和应变，计算岩体的法向刚度系数与切向刚度系数。李宁等(1998)认为室内试验确定kn与ks存在取样制样复杂易扰动、代表性不强、初始压力难以确定等缺点，野外试验则成本昂贵、不易操作，于是提出在位移等效及应变等效的基础上利用声波技术在现场测试无充填及有充填结构面的刚度的方法。

根据测试方法的不同，结构面刚度可分为静态刚度与动态刚度。参考国际岩石力学与工程协会(ISRM，1981)建议，基于准静态加载条件下的结构面变形曲线计算获得的刚度系数属于静态刚度系数。岩体结构中弹性波传播至结构面处将会发生反射现象和透射现象，弹性波携带的能量在结构面处将重新分配，这一现象与结构面的动态刚度系数密切相关。Pyrak-Nolte et al.(1990)基于位移不连续模型(DDM)利用超声波透射系数反算了结构面法向刚度系数，并且与单轴压缩试验的结果吻合较好。基于应力波传播反算得到的结构面刚度系数是一种动态的刚度系数。周剑等(2013)基于应力波穿越结构面后的时延特征，给出了结构面动态刚度系数的反演方法。尽管结构面刚度系数一直作为岩体工程静态变形分析(赵海军等，2019；高相波等，2020)及动力过程计算的输入参数(李宁等，1998；田小甫等，2007)，动态与静态刚度系数两者之间的关系尚未形成一个明确的认识。

离散元法是一种非连续介质力学分析方法，其在模拟裂隙岩体结构面静态及动态力学行为方面有着比较独特的优势。离散元法在裂隙岩体中弹性波传播的研究方面得到了很好的应用。郭易圆等(2002)依据离散单元法编制了计算程序研究了有限长岩杆中纵波的传播，模拟得到杆中波形与解析解近似，并讨论了软弱夹层对应力波传播的影响。Toomey et al.(2000)基于离散元的思想，利用弹性圆形颗粒按六边形的形状规则排列建立连续介质模型，在不考虑介质阻尼情况下进行地震波传播的模拟，该模拟结果与高阶差分方法计算得到的地震波形非常吻合。Resende et al.(2010)利用颗粒流方法从建模、动静态边界条件及吸收边界处理、颗粒粒径与波长比值、结构面力学特征、应力波频率等方面研究了岩块及含结构面岩体中的应力波传播特点，模拟获得的结构面处应力波的透反射系数与DDM方法预测的基本一致。

鉴于当前岩体结构面动态与静态刚度系数两者的对比研究尚不深入，本文从细观力学角度利用离散元数值模拟方法，开展岩体结构面的拟静态加载试验模拟及应力波传播模拟，探索结构面动态与静态刚度系数的相关性。拟静态加载模拟中，基于PFC2D(Particle Flow Code 2 Dimension)中接触模型的二次开发，构建了分段线性接触模型，用以研究不同法向应力条件下结构面的非线性变形特征，并据此计算结构面的静态法向刚度系数。同时，利用应力波透射系数反算结构面动态法向刚度，并与之对比。

1 分段线性接触模型

Cundall(1971)首先提出了离散单元法，将颗粒介质的运动及其相互作用采用圆形(或异型)离散单元来模拟，每一时刻颗粒在平面内的位置和速度由平动和转动运动方程来确定。PFC2D即二维颗粒流程序，是以圆形颗粒介质的运动及其相互作用为研究对象的一种离散单元方法。该方法通过将实际的材料离散成由若干个刚性颗粒组成的模型，来研究实际材料的各种力学特性(Potyondy et al.，2004)。颗粒流方法以牛顿第二定律和力-位移定律为基础，采用显式差分算法，循环应用牛顿定律分析颗粒的运动特征、力-位移定律分析颗粒的接触特征，直到所有颗粒都不再出现不平衡力和不平衡力矩为止，从而实现对颗粒介质的运动及其相互作用过程的模拟。

在PFC2D程序中提供的接触关系模型包括线接触刚度模型和简化的Hertz-Mindlin接触模型，其中Hertz-Mindlin接触模型是一种非线性的模型，适用于无黏性散体介质的模拟，不能应用于连续介质模拟中。大量的试验结果表明，由于结构面两壁面上相互接触的凸起体形态不规则、分布不均匀，结构面法向受力与对应的变形呈现非线性关系。为了较为准确描述结构面非线性变形行为，在颗粒离散元程序中建立假设：颗粒在受力条件下出现相互嵌入的现象，随着嵌入的深度(dn)增加，颗粒的相互作用力与颗粒嵌入深度宏观上呈非线性关系。利用 C++ 语言开发一种分段线性接触模型(图1)来近似模拟颗粒接触的非线性行为，并嵌入到PFC2D程序中分析结构面动/静态刚度系数的关系。

图1 分段线性接触模型示意图Fig.1 Schematic diagram of multistage linear contact model

圆形颗粒按六边形规则排列组合形成计算模型，模型中间设置一条结构面(图2)，结构面用红色直线表示，并设定结构面处的接触模型为自行开发的分段线性接触模型。图2所示模型中左右两侧及下部的墙体位置不变，参考Zhang et al.(2013，2014)关于颗粒流模拟计算中加载速度的建议，设置顶部墙体以0.005m·s-1的速度向下加载，使模型产生变形。根据线性位移引伸计的原理，监测结构面位置接触点两侧的位移得到结构面法向压力-变形之间的关系曲线(图3)。图3中所示模拟获得的结构面力-变形曲线呈分段线性特征，与图1所示接触模型特征基本一致，其表明自行开发的分段线性接触模型是可靠的。

图2 颗粒按六边形组合方式构建的计算模型(含一条结构面)Fig.2 The model containing a fracture in the middle assembled by particles in the hexagon way with particles

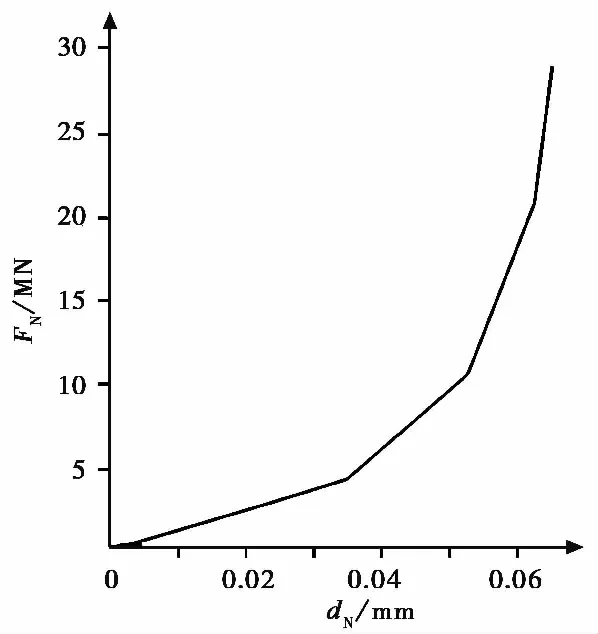
图3 结构面法向压力随变形的关系曲线Fig.3 The curve of normal force with deformation of a fracture

2 基于PFC2D的应力波传播模拟

建立基于颗粒方法的长杆模型如图4所示，该模型由半径为0.25m的圆形颗粒按矩形方法排列而成，模型长度为150m，宽度为5m。模型中微观颗粒的密度为3347.09kg·m-3，颗粒的法向刚度和切向刚度均为120GPa·m-1，颗粒间的摩擦系数取为0.5，为确保模型在应力波作用下不会产生破坏，颗粒间的黏结强度设为非常大值，并设定颗粒在应力波作用下运动时不受阻尼的影响。长杆模型被结构面分开为左右两部分，结构面刚度系数对应力波传播产生显著影响。将结构面刚度系数归一化处理，设结构面归一化法向刚度

图4 颗粒呈矩形排列的颗粒流模型Fig.4 Particle flow model for rectangular array of particles

Kn=kn/ρCpω

式中：kn为法向刚度系数；ρ为模型密度；Cp为模型中纵波波速；ω为应力波的频率。模拟中设定结构面的归一化法向刚度Kn取值从0.1变化到5.0。模型左端输入频率为100Hz，振幅为0.1的余弦波(式(1))，从结构面两侧模型1/4和3/4位置分别获取通过不同刚度结构面的透反射波如图5a和5b所示。提取入射波与透射波的波幅计算应力波透射系数，并与解析解对比发现：基于PFC2D模拟方法得到的应力波通过不同刚度结构面的透射系数与解析解吻合较好(图6)。

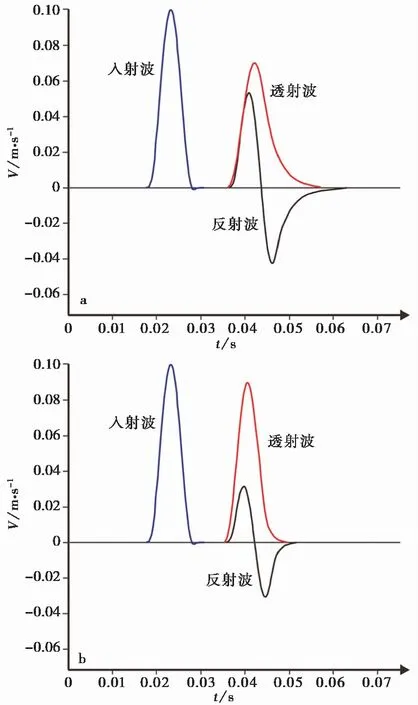
图5 应力波通过两种不同刚度结构面的透反射图Fig.5 Transmission and reflection diagrams of stress waves passing through fractures with different stiffnessa.Kn=0.6；b.Kn=1.0

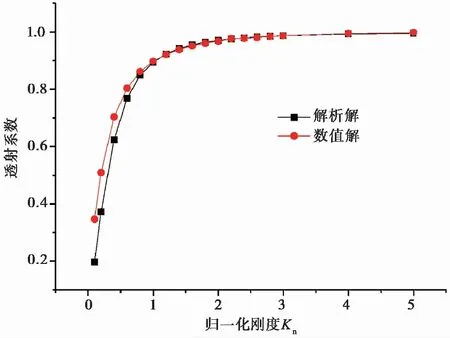
图6 应力波透射系数随结构面归一化刚度系数变化的曲线Fig.6 The curves of the transmission coefficient of stress wave under various normalized fracture stiffnesses

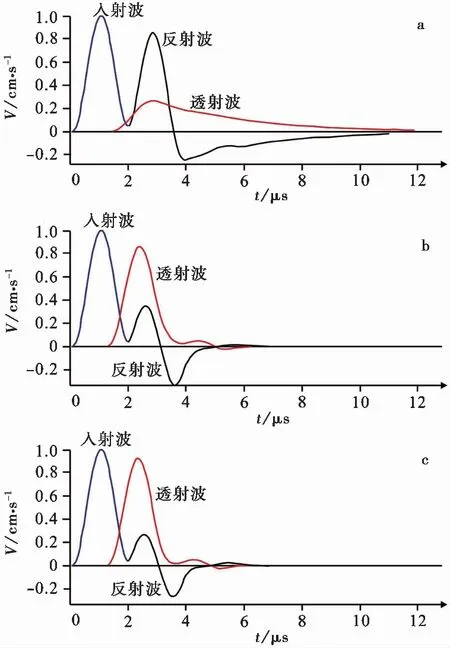
u(t)=(1-cos2πf0t)/2 0

(1)

式中：f0为输入波频率。

3 应力波吸收边界条件

在颗粒离散元模拟计算中，通常在模型的边界上定义一定宽度范围内颗粒组成的条带作为力或者其他边界条件的实施对象，如图7所示模型顶底部绿色和红色颗粒组成的条带可作为静力与动态冲击荷载作用的对象。与连续介质力学中采用应力边界不同，在颗粒离散元模拟中不能直接施加应力边界条件，往往只能将应力转化为力作用于模型边界的颗粒中心。假定计算时在图7所示的模型顶底部施加应力σ，我们将该应力等效为作用在模型顶底边界上半径为rball颗粒中心的作用力Fball。

Fball=σ·2rball

(2)

式(2)表明，由于边界上颗粒半径大小不一，因此作用于不同半径颗粒中心的力也不同。如图7所示，模型两端的颗粒大小和排列都不规则，等效力需要分别施加于端部颗粒上，如果仅仅选择模型两端最外层的颗粒用以施加等效力则会产生误差。因此，我们选择模型两端一定厚度范围内(3～4倍颗粒平均直径)的颗粒层来施加等效力，尽量减小颗粒尺寸不均匀带来的误差。以图7所示模型顶部绿色颗粒区作为施加静态应力边界条件的研究对象，顶部宽度为W，绿色颗粒区的颗粒数量为N，则每个颗粒上作用力Fball表达式为：

图7 颗粒随机排列组合的PFC2D模型Fig.7 PFC model assembled by random particles

(3)

式中：Bcoef为施加边界条件的颗粒层厚度的修正系数；ri(i=1～N)为施加边界条件的颗粒层内的颗粒半径。

计算动力学问题时，由于模型尺寸的限制，在模拟无限区域内应力波传播时往往需要设置吸收边界条件来消除有限边界对应力波的反射。在当前实现应力波吸收边界条件的方法中，Lysmer et al.(1969)提出的方法被广泛应用在各类数值模拟的软件中，比如，Itasca公司的数值模拟软件中(除PFC2D和PFC3D)均提供了该方法。PFC2D程序中只能间接实现边界吸收条件。根据波前面动量守恒，有：

σ=ρ·c·v

(4)

式中：σ为介质中的应力；ρ为介质的密度；c为波速；v为质点运动速度。

应力波垂直入射自由边界处时，其反射波是与入射波对称的波，入射波与反射波在自由边界附近的叠加，质点的振动速度加倍。引入吸收边界条件的目的是消除自由边界的反射波。根据应力-速度关系式(4)可知，在自由边界面上施加应力σabsorb可消除自由边界的反射，vball是边界层各个颗粒的运动速度。

σabsorb=ρ·c·(-vball)

(5)

根据静态条件下推导的边界力与应力的转换关系式(5)，在实现吸收边界条件时，边界层内每个颗粒中心的作用力Fball-absorb的表达式为：

(6)

建立颗粒随机排列的数值模型如图7所示。图7中模型高宽分别为10mm和5mm，其微观参数可参见表1。模型顶部和底部的两种不同颜色所示的边界层均设置吸收边界条件，吸收自由面的反射波，模型中间设置三排监测点用来监测应力波传播时模型质点运动情况。该模型被近视直线型的结构面切割，结构面的归一化刚度Kn取1.0时，从模型的底部输入频率为1MHz、振幅为0.01m·s-1的余弦波，底部和中部监测点获得的入射波、反射波和透射波速度波形曲线如图8，模型端部的反射波完全被吸收。结构面的归一化刚度Kn介于0.1～5.0，经一系列的计算得到不同Kn条件下的应力波的透射系数(图9)。图9表明当Kn≥0.2时应力波穿过颗粒随机排列组合形成的模型中近似平直结构面的透射系数与解析解也基本一致；当Kn=0.1时由于模拟得到的透射应力波频率较入射波发生较大变化，此时不能直接利用透射波幅值计算应力波透射系数跟解析解进行比较。总的来说，图9进一步说明了基于PFC2D模拟应力波传播是可行的。

表1 图7所示模型中的微观参数Table 1 Microscopic parameters in the model shown in Fig.7

图8 图7所示模型中结构面归一化Kn=1.0时透反射应力波曲线Fig.8 Transmission and reflection stress wave curves for normalized Kn=1.0 in the model shown in Fig.7

图9 应力波穿过颗粒随机的PFC模型中结构面的透射系数Fig.9 Transmission coefficient of stress wave passing through the fracture in a PFC model assembled by random particles

4 结构面动-静态法向刚度对比

选择Barton结构面分级中的第一种结构面(JRC=0～2)作为参考对象，构建含结构面岩体的数值模型，并结合上述分段线性接触模型，分别基于轴向加载和应力波传播两种方式研究结构面在不同受力条件下法向刚度系数变化趋势。首先，建立含结构面岩体的颗粒流模型，可分为3步(图10)：(a)建立颗粒随机分布的完整块状模型；(b)删除块状模型中间的部分颗粒产生上、下两个次级块体模型；(c)使上、下两个次级块体模型靠拢，结构面逐渐闭合。其次，对结构面处的接触点依据分段线性接触模型赋值对应的细观力学参数。最后，采用逐步加载的方式对该模型进行轴向加载，获取结构面的力-变形之间的关系曲线。

图10 建立含结构面岩体的颗粒流模型的步骤Fig.10 Steps for establishing PFC model of rock mass with a fracture

为体现结构面的非线性特征，本研究中采用4段线性接触模型模拟结构面处颗粒的接触变形行为。图10所示模型中颗粒平均半径为0.022mm，设定颗粒嵌入深度dn分别为颗粒平均半径0.35倍、0.5倍、0.6倍作为分段线性接触模型中接触刚度的分界点，第1至第4段的接触刚度分别为1.5×109iN·m-1、3.0×109iN·m-1、1.5×1010iN·m-1和3.0×1010iN·m-1。图10所示的模型在正应力作用下的变形特征曲线如图11所示，结构面的非线性特征得到了很好的表示。依据图11所示的应力-变形曲线，分别计算结构面在不同变形量下对应的结构面刚度系数变化曲线如图12所示，结构面法向刚度系数取值范围介于2860～38700GPa·m-1。

图11 结构面数值模型法向应力-相对位移曲线Fig.11 Stress-displacement curve of the numerical fracture

图12 结构面法向刚度与变形量的关系曲线Fig.12 The curve of normal stiffness of a fracture varying its deformation

图10所示模型两端加载过程中，轴向应力每增加5MPa后保持压力恒定一段时间，从模型底部输入频率为500kHz，幅值为0.01的余弦脉冲波。模型中设置两排监测点分别记录入射波与透射波的波形。图13a～图13c所示分别对应的是正应力为10MPa、100MPa和200MPa时，入射波、反射波与透射波的波形曲线。根据入射波和透射波波形曲线计算得到不同压应力状态下对应的透射系数，再反算得到不同压应力状态下结构面动态法向刚度如图14所示。数值模拟结果显示结构面刚度系数介于2800～38700GPa·m-1之间，与Pyrak-Nolte et al.(1990)获得的平直原生结构面在0～85MPa压应力下的动态法向刚度值(2000～150000GPa·m-1)基本一致。模拟结果还表明：通过弹性波透射系数反算得到的结构面动态刚度系数与静态刚度系数之比值约为1.0，一般而言，岩体或岩体结构面的动态力学参数要大于静态力学参数(弹性模量、剪切模量、结构面刚度等等)。van Heerden(1987)通过测试干燥砂岩得到动态弹性模量是其静态弹性模量的1～3倍。Tutuncu et al.(1992)得到饱和砂岩的动态弹性模样与静态弹性模量的比值为1～6。Cai(2001)测试了混凝土制作而成的人工结构面分别在拟静态及20kHz声波条件得到的结构面刚度，发现利用声波方法得到的结构面在0～20MPa压应力作用下刚度取值范围为20～1200GPa·m-1，并且该刚度是拟静态条件下的1.2～2倍。Zhou et al.(2020)在单轴加卸载过程中对页岩、花岗岩人工结构面样品进行了力学测试和超声波测试，结果表明：加载初期两种人工结构面的动态刚度系数均高于静态刚度系数，随着法向应力增加动态刚度系数接近静态刚度系数。具体表现为：法向应力为15MPa时，动态法向刚度与静态法向刚度之比约为2.0，随法向应力的增加该比值接近1.0。

图13 不同压应力下应力波通过结构面后的透反射波Fig.13 Transmission and reflection waves of stress waves passing through the structural plane under different compressive stressesa.压应力为10MPa；b.压应力为100MPa；c.压应力为200MPa

图14 不同压应力作用下结构面动静态法向刚度变化曲线Fig.14 Dynamic and static normal stiffness curves of structural surfaces under different compressive stresses

与前人的试验结果相比，低应力条件下，本文中基于数值模拟获得的结构面动态刚度系数与静态刚度系数之比值要偏小；高应力条件下，模拟结果与试验结果基本一致。

5 结 论

结构面刚度系数一直作为岩体工程静态变形分析及动态过程计算的重要输入参数。然而，结构面动态与静态刚度系数两者之间的定量关系尚未形成确定的认识。建立动/静态刚度系数相关性的经验公式，实现两者数值之间的转换，可方便不同工况下岩体工程计算中结构面参数取值。基于准静态加载条件下的结构面变形曲线计算可获得其静态刚度系数。岩体中应力波传播至结构面处将会发生反射现象和透射现象，利用应力波在结构面处的透反射系数可以反演计算结构面的动态刚度系数。本文中运用颗粒离散元数值模拟方法，开发新型接触本构模型，实现了结构面动、静态刚度系数的对比研究，取得了以下认识：

(1)颗粒流程序PFC2D中提供的接触本构无法准确描述结构面非线性变形行为。结合结构面壁面凸起体受力后的非线性变形特征，利用C++语言开发一种分段线性接触模型。该模型加载至PFC2D中，实现了结构面的非线性变形特征的模拟。

(2)通过黏结接触模型将离散圆形颗粒组合，实现了完整长条形岩块中应力波传播模拟。在模型中设置一条结构面，模拟再现了应力波在结构面处的传播特征，并发现：基于颗粒流模拟方法得到的应力波通过不同刚度结构面的透射系数与解析解相吻合。

(3)利用离散颗粒流方法在有限大小介质中实现无限介质中应力波传播模拟尚无直接可用于消除边界反射的模型。基于连续介质力学中的黏滞吸收边界条件，在PFC2D模型边界设置等效阻尼力，实现了垂直入射平面应力波吸收边界条件的应用。

(4)构建含结构面岩体模型，结构面接触部位设置分段线性接触模型，通过模拟单轴压缩试验与应力波传播分别获得了一致性较好的结构面动、静态刚度系数，模拟获取的结构面动/静态刚度系数之比值约为1.0。

本研究中的认识还存在一定的不足，在低应力条件下，基于数值模拟获得的结构面动、静态刚度系数之比与室内试验结果存在一定的差异，另外还需要从结构面粗糙度方面加以考虑，开展进一步的研究。