基于数字图像处理的矿物颗粒形态定量分析*

陈建湟 张中俭 徐文杰 李丽慧

(①中国地质大学(北京)工程技术学院，北京 100083，中国)(②清华大学水沙科学与水利水电工程国家重点实验室，北京 100084，中国)(③中国科学院地质与地球物理研究所，中国科学院页岩气与地质工程重点实验室，北京 100029，中国)

0 引 言

岩石薄片鉴定是在偏光显微镜下鉴定矿物和岩石的一种方法。它具有经济、快捷、直观的特点，在石油天然气勘探(Srisutthiyakorn et al.，2018)、石质文物保护(Reedy，2013；张中俭等，2015)等领域应用广泛。目前，我国《岩石薄片鉴定规范》(SY/T 5368-2016)采用目估法对薄片中矿物的成分、含量、结晶特点、光学性质、结构、构造和生成顺序进行鉴定，确定岩石类型及其成因特征。该规范分别采用粒度和磨圆度对矿物颗粒大小和形态进行评价。粒度指矿物颗粒轮廓的最小外接圆，通过比对岩石薄片显微照片上的比例尺目估得到。磨圆度的评价方法是将待测矿物颗粒图像和已标定形态特征的图像进行比对。根据《岩石薄片鉴定规范》和Krumbein et al.(1963)的研究，将磨圆度的值按照一定区间分为棱角(0～0.15)、次棱角(0.15～0.25)、次圆(0.25～0.4)、圆(0.4～0.6)、极圆(0.6～1.0)5个等级。这种方法具有方便、快捷的优点，但其评价结果受测试人主观选择的影响，并且仅用磨圆度不能刻画矿物颗粒的全部特征。

在颗粒形态量化研究领域中，研究人员对砂颗粒的形态研究较早。目前，砂颗粒的形态特征可以采用球度S、凸度C、长宽比A和磨圆度Π等4个独立参数来刻画(Wadell，1932；Blott et al.，2008；Altuhafi et al.，2013；Liu et al.，2018)，如图1所示。这4个形态参数分别用于描述颗粒的近圆程度、凹陷程度、狭长程度和棱角的尖钝程度，式(1)～式(4)分别给出了相关计算公式：

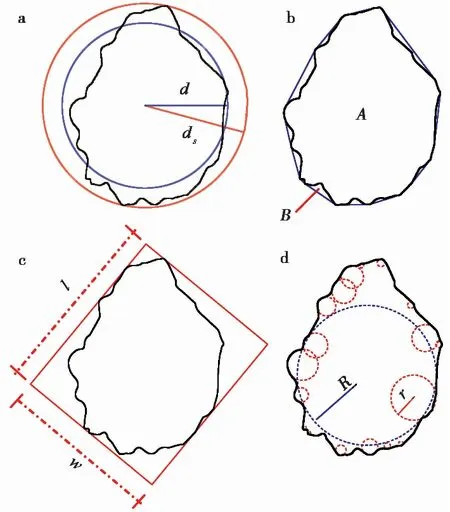
图1 颗粒形态参数计算示意图Fig.1 Schematic diagram of particle shape parametersa.球度；b.凸度；c.长宽比；d.磨圆度

球度S的计算公式：

(1)

式中：d为颗粒等效面积圆的半径；ds为颗粒的最小外接圆半径。

凸度C的计算公式：

(2)

式中：AS为颗粒的面积；BS为颗粒凸包线的面积。

长宽比A的计算公式：

(3)

式中：w为颗粒最小外接矩形的短边；l为颗粒最小外接矩形的长边。

磨圆度Π的计算公式：

(4)

式中：ri为颗粒棱角的曲率半径；R为颗粒的最大内切圆半径；N为颗粒棱角数量。

图像处理是利用计算机对图像进行像素级处理、分析的过程。在工程地质方面，有学者利用图像处理技术开展地质体的细观力学性质(岳中琦等，2004；徐文杰等，2007a，2007b；赵洲等，2019；Xu et al.，2020)、碎屑流堆积体粒径(彭双麒等，2019)、岩性识别(胡启年等，2020)等方面的研究；还有学者利用图像处理技术分析岩石薄片图像从而计算矿物颗粒粒径分布(Seelos et al.，2005；袁瑞等，2015)，颗粒分形维数、球度、凸度等(Berrezueta et al.，2019)，颗粒间孔隙的孔喉比(刘春等，2018)，以及根据岩石薄片图像预测岩石的压缩性(Das et al.，2020)、弹性模量和渗透性(Saxena et al.，2016;Srisutthiyakorn et al.，2018)。

本文拟利用岩石薄片的显微图像，基于图像处理技术，借鉴砂颗粒的形态参数球度、凸度、长宽比和磨圆度等，全面、定量地刻画矿物颗粒的形态。对于球度、凸度、长宽比的参数，由于其计算仅涉及到颗粒的长度和面积等，可以利用现有的算法库进行求解(如OpenCV)，根据式(1)～式(3)可直接计算相应的参数。磨圆度的理论公式(即式(4))由Wadell(1932)提出。由于需要计算颗粒棱角的曲率半径、颗粒棱角的数量等参数，导致利用该公式难以直接计算出磨圆度。一些学者利用图像处理技术对单一颗粒进行磨圆度的计算。Zheng et al.(2015)首先用局部加权平均的方法将颗粒轮廓光滑处理，然后标记轮廓外凸的坐标点为棱角关键点，最后用全部棱角关键点按照递减棱角关键点的方式循环拟合圆，以达到搜索棱角圆的目的。该方法不独立对颗粒棱角进行识别，计算步数多且计算结果存在一定偶然性。Vangla et al.(2018)首先利用傅里叶级数拟合颗粒轮廓，然后将轮廓上曲率为0的部位作为不同颗粒棱角的分界，进行棱角识别，最后求得各个棱角中每个棱角关键点的曲率半径，挑选其中一个代表该棱角的曲率半径。该方法在棱角关键点识别中会引入棱角周边的点而导致棱角存在曲率渐变的情况，并且不容易挑选出代表该棱角的曲率半径。本文在傅里叶级数拟合颗粒轮廓的基础上，提出新的磨圆度计算方法，使计算结果更为客观、便捷，并且可以同时计算多个颗粒的磨圆度。

本文论述了计算球度、凸度、长宽比和磨圆度等形态参数的具体方法(尤其详细论述了磨圆度的计算方法)，利用已知形态参数的规则图形验证了该方法的准确性，利用薄片显微图像进行了矿物颗粒形态的计算应用，讨论了影响矿物颗粒形态计算结果的影响因素，展望了其应用前景。

1 矿物颗粒形态定量分析方法

本研究方法具体包括：岩石薄片制备和显微图像获取；利用图像分割技术区分矿物颗粒，提取矿物颗粒轮廓像素坐标；利用离散几何方法求解矿物的形态参数。

1.1 岩石薄片显微图像获取

根据《岩石制片方法》(SY/T 5913-2004)，对岩石样品进行薄片制作。将制作好的岩石薄片放置于偏光显微镜下观察并拍照，如图2a所示。

1.2 矿物颗粒分割和像素坐标提取

将岩石薄片的图像转换为灰度图，利用图像分割技术从岩石薄片显微图像中将不同矿物颗粒和背景区分开并转为二值图。因为单个矿物颗粒的灰度值通常相近，矿物颗粒之间的界限与矿物颗粒的灰度值相差较大，不同矿物颗粒以及颗粒边界占据不同灰度范围。根据这一特征，采用阈值分割法(Otsu，1975)对岩石薄片显微照片进行矿物颗粒分割。阈值分割法通过设定不同的特征阈值，将图像分为矿物颗粒和背景2类。由于岩石薄片显微照片背景复杂，先对颗粒进行着色，再进行图像分割。图2展示了某大理岩薄片显微照片及矿物颗粒分割结果。利用上一步得到的二值图通过Satoshi et al.(1985)提出的算法提取矿物颗粒轮廓像素坐标，并剔除超出图像边界的矿物颗粒。

图2 图像分割技术及矿物颗粒轮廓提取Fig.2 Image segmentation technology and extraction of mineral particle contoura.岩石薄片显微图片；b.矿物颗粒着色；c.利用阈值分割技术获取的矿物颗粒轮廓

1.3 矿物颗粒形态参数计算

1.3.1 球度计算

利用上述得到的矿物颗粒轮廓像素坐标，分别计算每个矿物颗粒的面积AS和最小外接圆半径ds，通过矿物颗粒面积求得其等效面积圆半径d，根据式(1)求解每个矿物颗粒的球度。

1.3.2 凸度计算

利用矿物颗粒轮廓像素坐标分别计算每个矿物颗粒的凸包线(Graham，1972)，进一步求解每个矿物颗粒凸包线的面积BS，在球度的计算过程中已经得到每个矿物颗粒的面积AS，根据式(2)可以求得每个矿物颗粒的凸度。

1.3.3 长宽比计算

利用矿物颗粒轮廓像素坐标分别计算每个矿物颗粒的最小外接矩形(Doytsher，1988)，根据式(3)将最小外接矩形的短边w比长边l，求得每个矿物颗粒的长宽比。

1.3.4 磨圆度计算

磨圆度的计算是本文重点论述的内容，也是本文具有创新性的内容，计算流程如图3所示。利用矿物颗粒轮廓像素坐标计算其最大内切圆半径R(刘书桂等，1998)，然后识别矿物颗粒各个棱角并利用最小二乘法依次拟合各个棱角圆，得到各个棱角的曲率半径ri，根据式(4)求得矿物颗粒的磨圆度。根据式(4)，颗粒棱角的识别范围为曲率半径小于最大内切圆半径的棱角，将上述棱角的坐标点定义为棱角关键点。将棱角关键点按照归属棱角的不同进行独立分组，使得颗粒的每个棱角对应若干个棱角关键点。这样，颗粒棱角的识别可分为棱角关键点识别和棱角关键点分组两个关键步骤。

图3 磨圆度的计算流程Fig.3 Calculation process of roundness

第1步，颗粒棱角关键点的识别包括颗粒轮廓光滑处理和颗粒棱角关键点标记两个过程：

(1)矿物颗粒轮廓放大后存在锯齿边，分辨率越低，锯齿边的波动幅度占矿物颗粒宽度的比重越大，对颗粒棱角识别的准确性影响越大，所以需要对颗粒轮廓进行光滑处理。具体做法是将颗粒轮廓从形心处按极坐标展开，利用傅里叶级数来拟合，并得到矿物颗粒轮廓的傅里叶级数关系式(图4)。另外，利用该关系式可以使分辨率过低的颗粒轮廓实现超分辨率，增加颗粒棱角轮廓的坐标点。

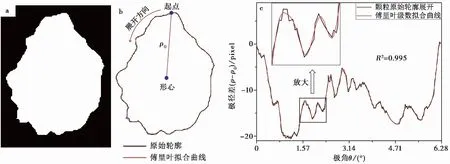
图4 利用傅里叶级数光滑颗粒轮廓Fig.4 Schematic diagram of smoothing particle contour based on Fourier seriesa.原始轮廓；b.极坐标展开示意图；c.傅里叶级数拟合曲线

(2)用光滑处理后的颗粒轮廓进行棱角关键点标记。在傅里叶级数拟合的颗粒轮廓上取相邻的3个轮廓像素坐标作一个圆，如果该圆的圆心在轮廓内部、半径小于最大内切圆半径、该圆没有超出轮廓，则标记这3个点的中间点。若以上条件不能同时满足，则不标记。满足上述条件的所有轮廓像素坐标即为颗粒棱角关键点(图5a)。

图5 颗粒棱角关键点识别(a)及棱角圆计算(b)Fig.5 Key points identification of particle edges and corners(a) and corner circle calculation(b)

第2步，按照不同棱角将颗粒棱角关键点划分成组。这些关键点组成全部棱角。每组关键点拟合一个圆，定为棱角圆。颗粒棱角关键点分组可分为初步分组和精细分组两个过程：

(1)采用统计分析的方法对关键点初步分为若干组。关键点具有属于同一棱角相对聚集、属于不同棱角相对分散的特点。设置一个长度df，当相邻两个棱角关键点的距离d小于df时，这两个棱角关键点为相同组；否则，这两个棱角关键点为不同组。

对于df的设置包括如下3个步骤：1)计算相邻两个棱角关键点的距离，得到最大距离dmax和最小距离dmin；2)利用式(5)计算相邻两个棱角关键点的距离归一化值P，P值分布密集的区间对应颗粒棱角区域，P值分布稀疏的区间对应非棱角区域；3)为了进一步区分P值为密集区间或稀疏区间，引入分组系数a，使得P∈[0，a)时为密集区间，P∈(a，1]时为稀疏区间。a值可以通过统计若干个颗粒图像的相邻两个棱角关键点的归一化值P的分布来确定。当P=a时式(5)所求得的d即为df，如式(6)所示。

(5)

df=a×(dmax-dmin)+dmin

(6)

(2)对上述初步分组的关键点进行棱角圆计算，分析是否对关键点进行精细分组。当初步分组计算的棱角圆存在下列情况之一时，认为棱角圆不契合原始轮廓，尚需对初步分组结果进行精细分组：1)拟合的棱角圆超出颗粒边界；2)拟合的棱角圆的傅里叶级数拟合优度R2过低；3)棱角关键点对应的圆心角过小。

棱角关键点的精细分组采用二分法，即将该组在组内最大间距处分为两组，将这两组分别拟合棱角圆。如果上述棱角圆仍存在上述3种情况之一时，则对新组重复二分，直到所拟合的棱角圆不存在上述情况或关键点的数量小于3时停止。图5b即为对图5a所示的棱角关键点进行精细分组后得到的棱角圆。

由以上论述可知，本文提出的磨圆度计算方法更为客观和简便，且能同时计算若干个颗粒的磨圆度。相比Zheng et al.(2015)所提出的方法，有效减少棱角圆拟合步数，减少了棱角识别的偶然性；相比Vangla et al.(2018)所提出的方法，该方法不存在曲率渐变的情况，并且不用从若干曲率半径中挑选代表。

2 结果验证与实例应用

为了评价该方法的准确性，用已知形态参数的理论图形进行验证(图6a)。表1给出了上述图形的各个形态参数的理论值和用本文方法计算的结果。根据表1可知理论图形的球度、凸度、长宽比和磨圆度计算结果最大绝对误差分别为6.2%、0.3%、0.6%和3.2%。图6b进一步展示了计算磨圆度时棱角圆的计算结果，可以看出计算的棱角与原始轮廓的棱角一致。因此，该方法的准确性得到了验证。

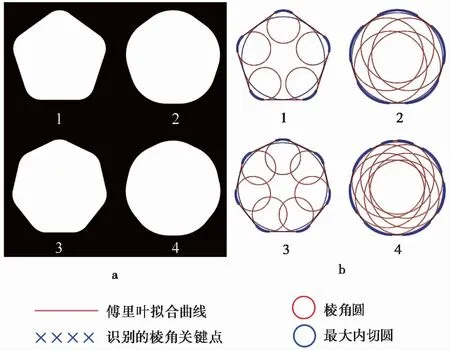
图6 已知形态参数的理论图形(a)及棱角圆计算结果(b)Fig.6 Theoretical figure with known shape parameters(a) and calculation result of corner circle(b)

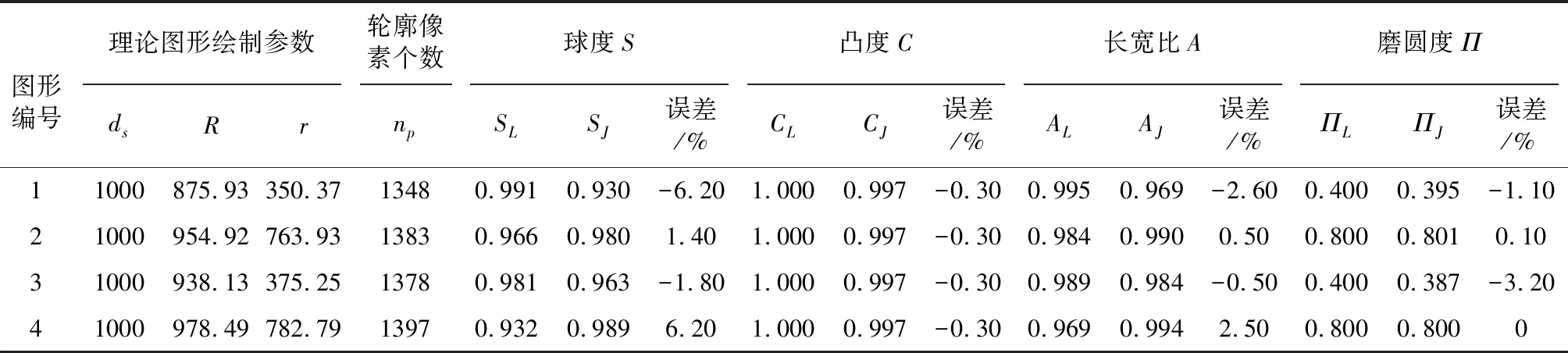
表1 理论图形的绘制参数和形态参数计算结果Table 1 Results of drawing parameters and shape parameters of theoretical graphs

图7 图2所示白云石矿物棱角圆的计算结果Fig.7 Results of corners circles of the dolomite minerals(see Fig.2)in micrograph

当计算的矿物颗粒的样本足够大时，就可以利用上述方法计算得到矿物颗粒形态参数的统计结果。该方法尤其适合砂岩、大理岩、石英岩、花岗岩等矿物颗粒形态参数的定量分析，因为这些岩石的矿物颗粒轮廓明显、排列紧密。

表2 图2所示白云石矿物颗粒的轮廓像素信息与形态参数计算结果Table 2 Pixel information of dolomite mineral particle profile(see Fig.2) and results of the shape parameters

3 形态参数计算的影响因素

矿物颗粒形态参数的计算结果可能受到多个因素影响，包括图像分辨率Re、颗粒轮廓的傅里叶级数拟合优度R2、棱角关键点分组系数a等，本文对上述影响因素进行了详细分析。

3.1 图像分辨率Re的影响

为了分析同一颗粒不同分辨率图像对颗粒形态参数计算的影响，将8张不同分辨率的图像分别进行颗粒形态参数计算，图片的具体信息及计算结果如表3所示。可以看出，在所选的图片尺寸范围内，颗粒的球度、凸度、长宽比的计算结果对Re较不敏感，磨圆度的计算结果对Re较敏感。

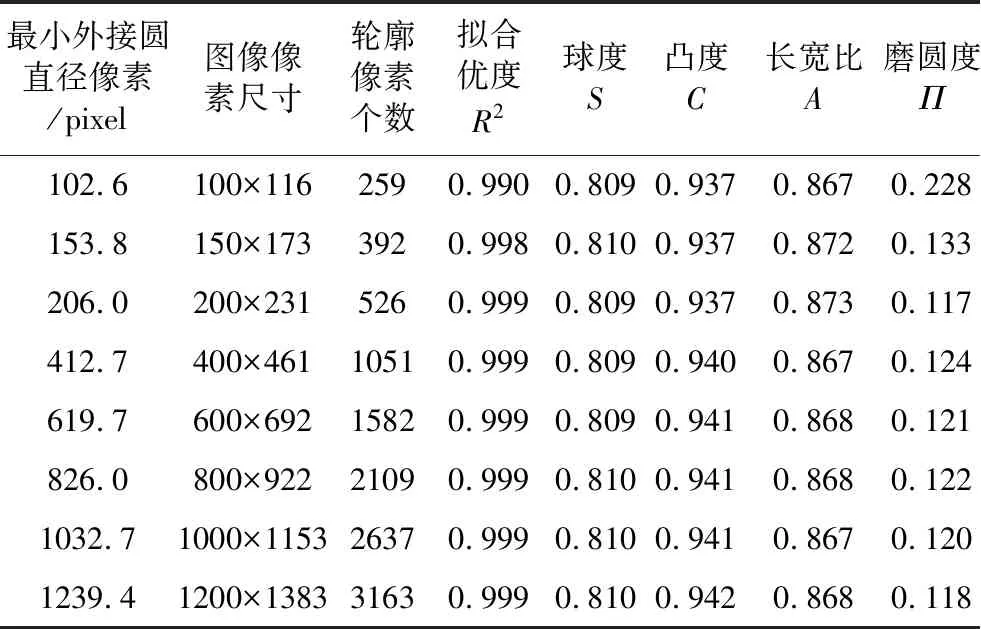
表3 同一颗粒不同分辨率的图像信息及其形态参数计算结果Table 3 Results of shape parameters of the same particle with different resolution

图8展示了4种不同图像分辨率下棱角圆的计算结果，可以看出：(1)不同分辨率图像对于颗粒棱角位置的识别都是准确的。在棱角区域，高分辨率图像与低分辨率图像都能够完全地识别颗粒棱角。(2)较高分辨率图像计算的棱角圆更小，说明高分辨率有助于还原颗粒的尖棱角，使得计算结果更加符合实际。在颗粒的最小外接圆直径像素数大于206 pixel之后，颗粒磨圆度的计算结果在0.12附近波动(图9)，且拟合的棱角圆结果也相对固定。所以，为保证磨圆度计算结果准确，颗粒的最小外接圆直径像素数下限约为200 pixel。

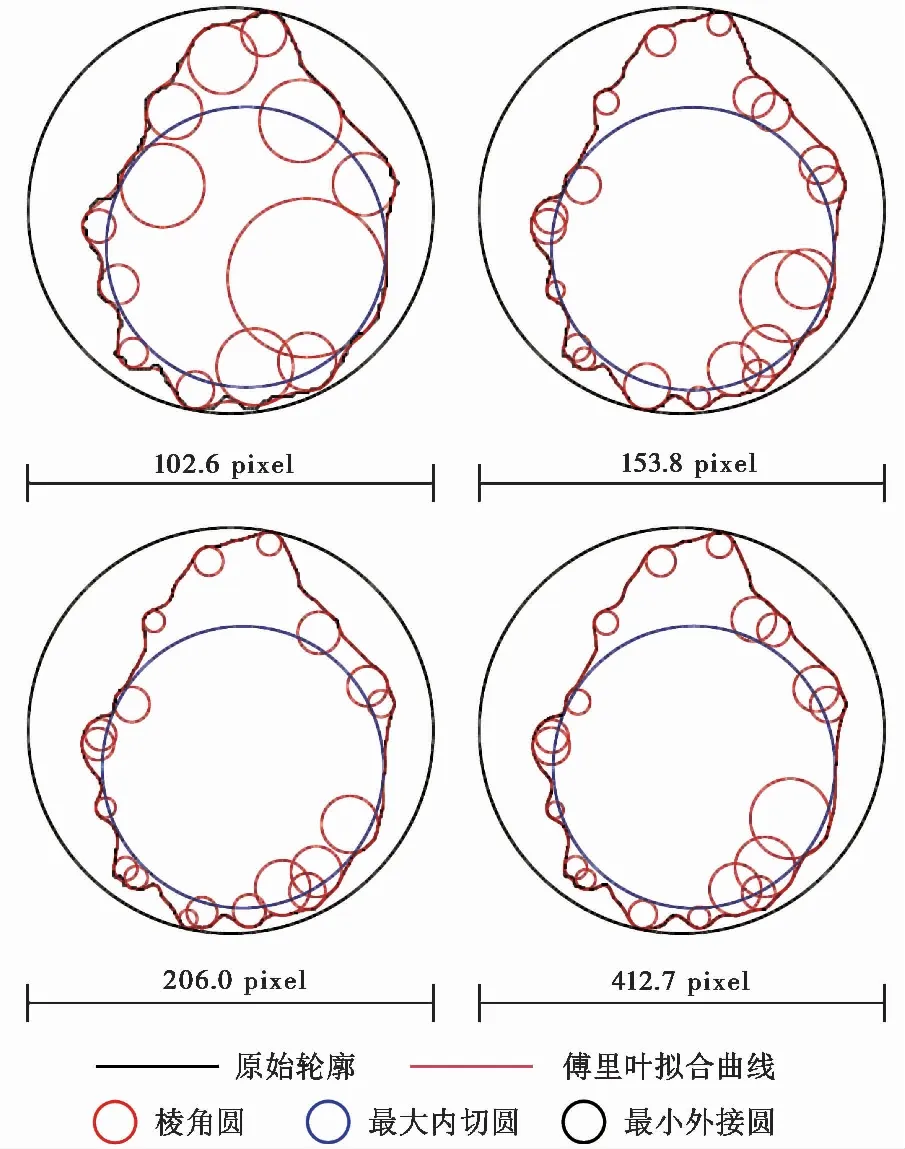
图8 不同图像分辨率棱角圆计算结果Fig.8 Results of corners circle with different image resolution

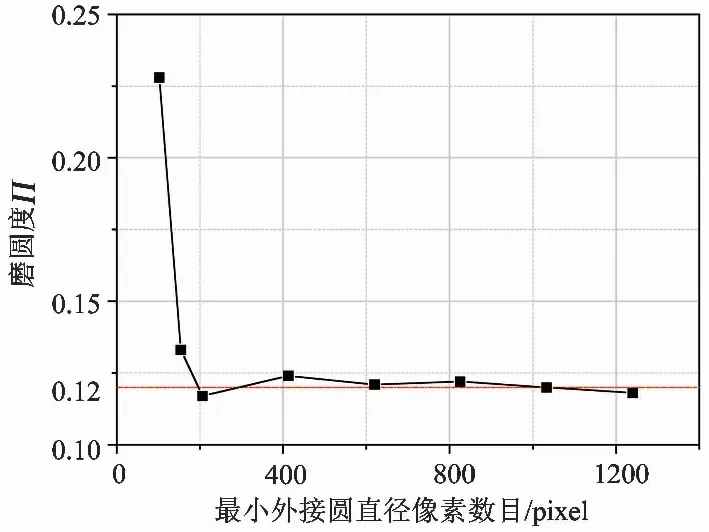
图9 最小外接圆直径像素数目与磨圆度计算值的关系Fig.9 The relation between the pixel numbers and the roundness values

3.2 傅里叶级数拟合优度R2的影响

对于球度、凸度、长宽比这3个形态参数，颗粒图像的锯齿边对其影响不大，计算时不需要对颗粒轮廓进行光滑处理，所以傅里叶级数拟合优度R2对球度、凸度、长宽比这3个形态参数没有影响。

为了分析同一颗粒、同一分辨率图像下，不同R2对磨圆度计算结果的影响，对一个磨圆度理论值为0.2、最小外接圆直径像素数为197 pixel的图形(图10a)进行傅里叶级数拟合。傅里叶拟合项数n分别为10～75。图11展示了n、R2、Π值两两之间的关系，可以看出：

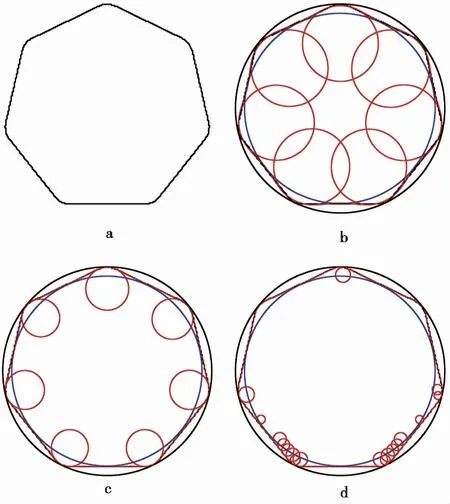
图10 不同傅里叶级数拟合状态下的颗粒棱角圆计算结果Fig.10 Results of particle corner circles under different Fourier series fitting statesa.颗粒原始轮廓；b.欠拟合；c.优拟合；d.过拟合

(1)对于n与R2而言，在n∈[10，75]范围内，随着n的增加，R2先快速增长后趋于稳定。

(2)对于n与Π而言，在n∈[10，20]范围时随着n的增加，Π值降低并趋于理论值0.2，在n∈[21，60]时，Π相对稳定在0.18左右，当n>60时，Π的计算结果波动较大。

(3)对于R2与Π值而言，根据磨圆度计算值与理论值接近的程度，将傅里叶级数拟合结果分为欠拟合、优拟合、过拟合3种情况(图10，图12)。与原始颗粒轮廓相比，欠拟合时，所拟合的轮廓更光滑，但颗粒棱角变钝，磨圆度计算值偏大；优拟合时，颗粒轮廓恰好光滑又不使颗粒棱角变形，磨圆度计算值与理论值基本相同；过拟合时，由于拟合的轮廓包含原始轮廓的锯齿边，所拟合的轮廓不光滑，程序误将锯齿边识别为颗粒棱角，造成磨圆度计算值波动。

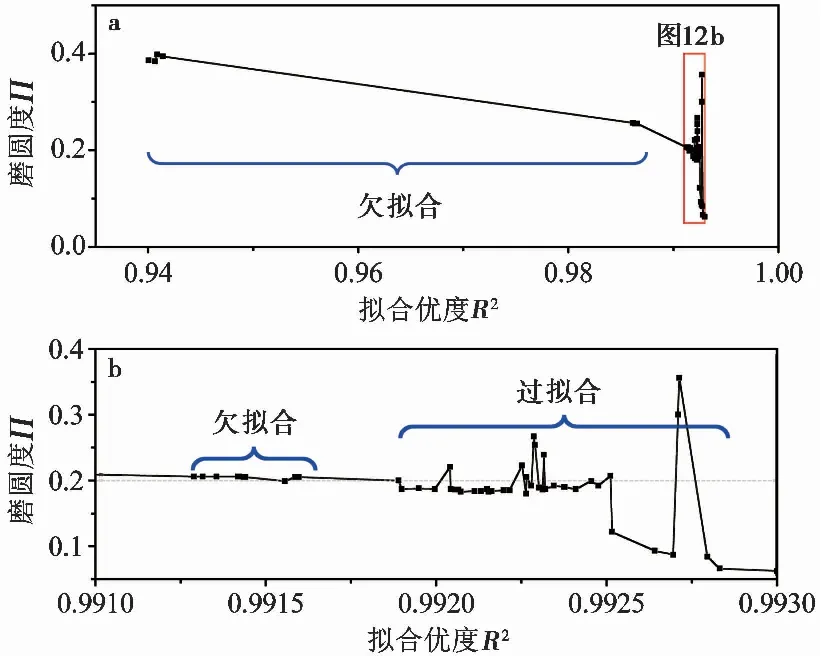
图12 根据R2和Π划分不同傅里叶级数拟合状态Fig.12 Different Fourier series fitting states according to R2 and Π

总之，傅里叶级数拟合优度R2的选取与锯齿边的振幅有关。存在一个最优的R2范围，R2大于该范围则过拟合，会把颗粒的锯齿边也拟合进来；R2小于该范围则欠拟合，棱角偏钝，计算的磨圆度结果偏大。

3.3 棱角关键点分组系数a的影响

根据1.3.4部分介绍的颗粒棱角关键点的分组方法，式(6)计算得到的df是判断相邻两个棱角关键点是否属于同一个棱角的标准，现对棱角关键点分组系数a的取值进行讨论。

为了分析a的合理取值，本文统计了20个颗粒图形(Krumbein et al.，1963)的相邻两个棱角关键点的距离归一化值P(见式(5))，如图13所示。这20个颗粒图形P值小于0.1的比重占到88.8%。根据本文1.3.4所述，a值尽量小、P

图13 所统计的20个颗粒图像的P值分布图(a)及其不同区间占比统计(b)Fig.13 Value distribution map of P based on 20 particle images(a) and its proportion of different intervals(b)

本文将P值分布区间在[0，1]区域内进行10等分，得到的a值可精确到十分位。若要a值精度更高，按照上述统计方法，将P值分布区间在[0，1]区域内进行更多等分即可。对于本文所介绍方法，a=0.1满足对棱角关键点进行初步分组的要求。

4 结论与展望

本文基于图像处理技术提出了同时进行若干矿物颗粒形态参数(包括球度、凸度、长宽比和磨圆度)定量分析的方法。该方法分为3个步骤：制备岩石薄片和获取显微图像；利用图像分割技术区分矿物颗粒，提取矿物颗粒轮廓像素坐标；利用离散几何方法求解矿物颗粒的形态参数。尤其对于磨圆度的计算，本文在傅里叶级数拟合颗粒轮廓的基础上，创新性地提出了棱角关键点识别和棱角关键点分组两步走的方法，前者包括颗粒轮廓光滑处理和颗粒棱角关键点标记两个过程，而后者包括初步分组和精细分组两个过程。

本文分析了图像分辨率Re、傅里叶级数拟合优度R2、棱角关键点分组系数a对形态参数计算结果的影响，发现：(1)球度、凸度、长宽比的计算结果基本不受Re和R2的影响；(2)磨圆度的计算结果受Re和R2的影响，建议计算磨圆度时颗粒最小外接圆直径像素数大于200 pixel，存在一个最优的R2范围，在这个范围内计算的磨圆度结果接近理论值；(3)当a精确到十分位时，确定a取值0.1最为合理。

本文所提出的方法未对矿物种类进行区分，未来可将矿物薄片的人工鉴定程序计算机化，通过机器学习与数据挖掘的方法来识别矿物种类，再按照矿物种类进行形态参数量化分析，并建立矿物颗粒形态参数的数据库，利用矿物颗粒的形态研究地质演变过程、岩石颗粒力学行为，从而使该方法具有更高的科学和实用价值。