基于ANSYS无制动结构钢吊车梁加固后的力学性能研究

陶 龙， 邓亨长， 徐国挺， 李清培

(1 四川公路桥梁建设集团有限公司， 成都 610093； 2 四川路桥华东建设有限公司， 成都 610500)

0 引言

门式刚架轻型房屋钢结构在工业厂房中应用广泛。在使用过程中，其自身承载力常受其他因素影响，为保证安全需对其进行加固，其中吊车梁加固是重点环节[1-2]。

李斌等[3]提出采用高强螺栓将角钢与腹板及上翼缘连接起来的方式加固无制动结构钢吊车梁。郑山锁等[4]提出采用钢斜撑加固无制动结构钢吊车梁。晏金炜等[5]对特重级无制动结构钢吊车梁加固进行研究，提出采用焊接方式增大钢梁截面尺寸来提高钢吊车梁的性能。施澄宇[6]结合钢结构厂房加固改造工程实践，采用增大截面法加固无制动结构钢吊车梁。于志强等[7]对轨道偏心荷载作用下大吨位无制动结构钢吊车梁进行分析，提出采用斜板加固方法提高钢吊车梁力学性能。

某工地钢筋加工场为单跨门式刚架轻型房屋钢结构厂房。厂房内设有工作级别A3级LD5T的电动单梁桥式起重机。吊车梁(图1)采用Q235B型钢HN396×199×7×11，为跨度6m的简支梁，加劲肋厚6mm，加劲肋间距750mm，加劲肋下端距下翼缘50mm。受后期生产需要，厂房荷载增加，将起重机换成一台LD16T电动单梁桥式起重机(最大轮压111.5kN，吊车轮距3m)后，吊车梁不能满足新的工作要求，需对其进行加固。

图1 6m简支吊车梁

1 无制动结构钢吊车梁受力模型

无制动结构钢吊车梁主要承受荷载：1)竖向荷载，即吊车轮压，设计值F，见式(1)；2)横向水平荷载，即吊车横向水平制动力，设计值T，见式(2)；3)纵向水平荷载，即吊车刹车力。由于吊车刹车力通过吊车梁传递给柱间支撑，对吊车梁影响不大，可不考虑。

F=γQα1Fkmax

(1)

式中：γQ为荷载分项系数，取值1.4；α1为荷载动力系数，取值1.05；Fkmax为吊车最大轮压标准值。

T=γQTk

(2)

式中：Tk为荷载标准值，Tk=ξ(Q+G)/n，其中，ξ为横向荷载系数，取值10%，Q为吊车额定起重量，G为横向小车重量，G=0.4Q，n为吊车车轮总数。

吊车梁上轨道偏心(偏心距e)会使竖向荷载F产生附加扭矩Mv=Fe；同时作用在轨顶的横向荷载相对于吊车梁剪心距离a会产生附加扭矩MH=Ta；因此吊车梁实际受力模型是双向弯曲和扭转的联合作用(图2)。

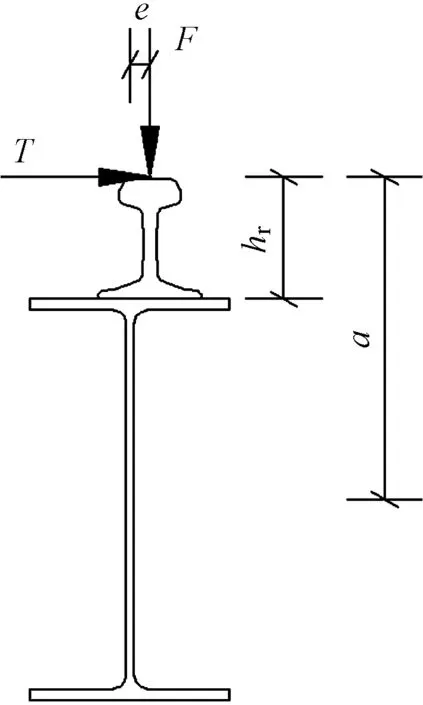
图2 吊车梁实际受力情况

2 有限元模型建立及验证

2.1 有限元模型建立

无制动结构钢吊车梁在双向弯曲和扭矩联合作用下会发生大转角、大变形，这种几何非线性特征会对结构受力特性产生影响。为深入研究无制动结构钢吊车梁加固方案在弹性及弹塑性阶段的受力性能，吊车梁模拟采用三维壳单元Shell181。

钢材弹性模量E=2.06×105N/mm2，泊松比ν=0.3，屈服强度fy=235N/mm2，采用双线性等向强化模型Biso，切线模量取0.01E。材料屈服判断依据von Mises屈服准则及Mises流动法则。在求解时打开大应变以及应力刚化选项来考虑几何非线性问题。简支钢吊车梁边界条件为：约束梁两端上下翼缘竖向位移；约束两端腹板侧向位移；约束一端下翼缘纵向位移。

模型荷载加载：将作用在轨顶的竖向荷载F转化为作用吊车梁上翼缘的竖向荷载F及附加扭矩Mv=Fe，将作用在轨顶的横向水平荷载T转化为作用上翼缘的横向水平荷载T及附加扭矩MH1=Thr，hr为吊车梁上的轨道高度(图2)。模型加载见图3。

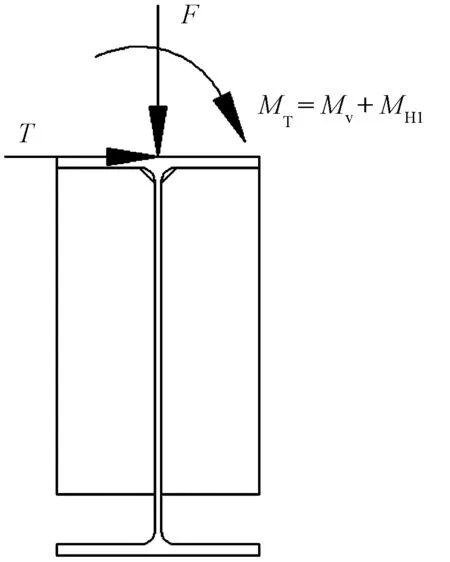
图3 ANSYS模型加载示意图

2.2 有限元模型验证

文献[8]对简支H型钢梁、工字钢梁和槽钢进行了稳定性试验研究，以跨中集中力的偏心e、跨中集中力与试件的夹角α两个参数来调整双向弯矩和扭矩值，并给出试验结果。本文选取其中具有代表性的HEB200钢梁模型来验证ANSYS模型的正确性，如图4所示。

图4 HEB200钢梁有限元模型

表1为HEB200试件试验结果及ANSYS分析结果，ANSYS分析结果与试验结果吻合良好。可见本文所选ANSYS模型参数基本正确，可有效模拟钢吊车梁的受力与变形。

HEB200试件试验结果与ANSYS分析结果对比 表1

3 原吊车梁力学性能及加固方案

3.1 原吊车梁的分析结果

表2为吊车荷载参数，力值比例系数β=T/F=0.047。通过影响线分析，吊车梁最大竖向弯矩245.86kN·m，最大横向弯矩11.53kN·m，最大剪力245.86kN。

吊车荷载参数 表2

根据《钢结构设计标准》(GB 50017—2017)[9](简称钢标)，按式(1)验算原吊车梁在双向弯曲作用下的强度、稳定性：

(3)

式中：Mx，My分别为绕截面主轴x，y轴的弯矩；V为沿腹板平面作用的剪力设计值；Wnx，Wny分别为对x，y轴的净截面模量；Wx，Wy分别为对x，y轴的毛截面模量；S为计算剪应力处以上毛截面对中和轴的面积矩；I为构件毛截面惯性矩；tw为构件的腹板厚度；γx，γy为对主轴x,y截面塑性发展系数；φb为梁整体稳定系数；f为钢材抗弯强度设计值；fv为钢材的抗剪强度设计值。

原吊车梁受弯强度验算值为299.88MPa，受剪强度验算值为99.06MPa，β=0.047时，竖向临界荷载为93.17kN。经验算，原吊车梁受弯强度、稳定性不满足设计规范要求。

选取弯矩最不利工况(图5)，进一步探讨吊车梁在双向弯曲和扭转联合作用下的力学性能。

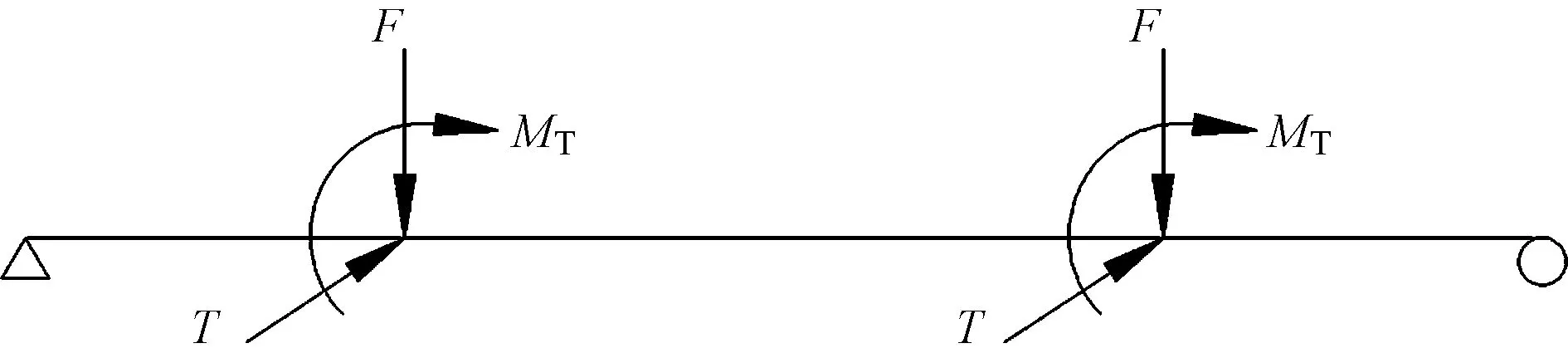
图5 6m简支吊车梁最不利受力简图

结果显示，加载至设计荷载的37.85%，即竖向临界荷载为62.04kN时，原吊车梁发生屈曲失稳，显然扭转效应的存在使吊车梁的临界荷载大大降低。

图6为原吊车梁屈服状态下截面各点位沿纵向的等效应力。可以看出，上翼缘应力首先达到屈服状态，腹板应力呈现出两端大、中间小的不均匀分布现象。在屈服状态下，吊车梁最大竖向位移达42.86mm，最大横向位移达79.37mm。可见在屈服状态下，吊车梁的竖向、横向刚度均相对较小。

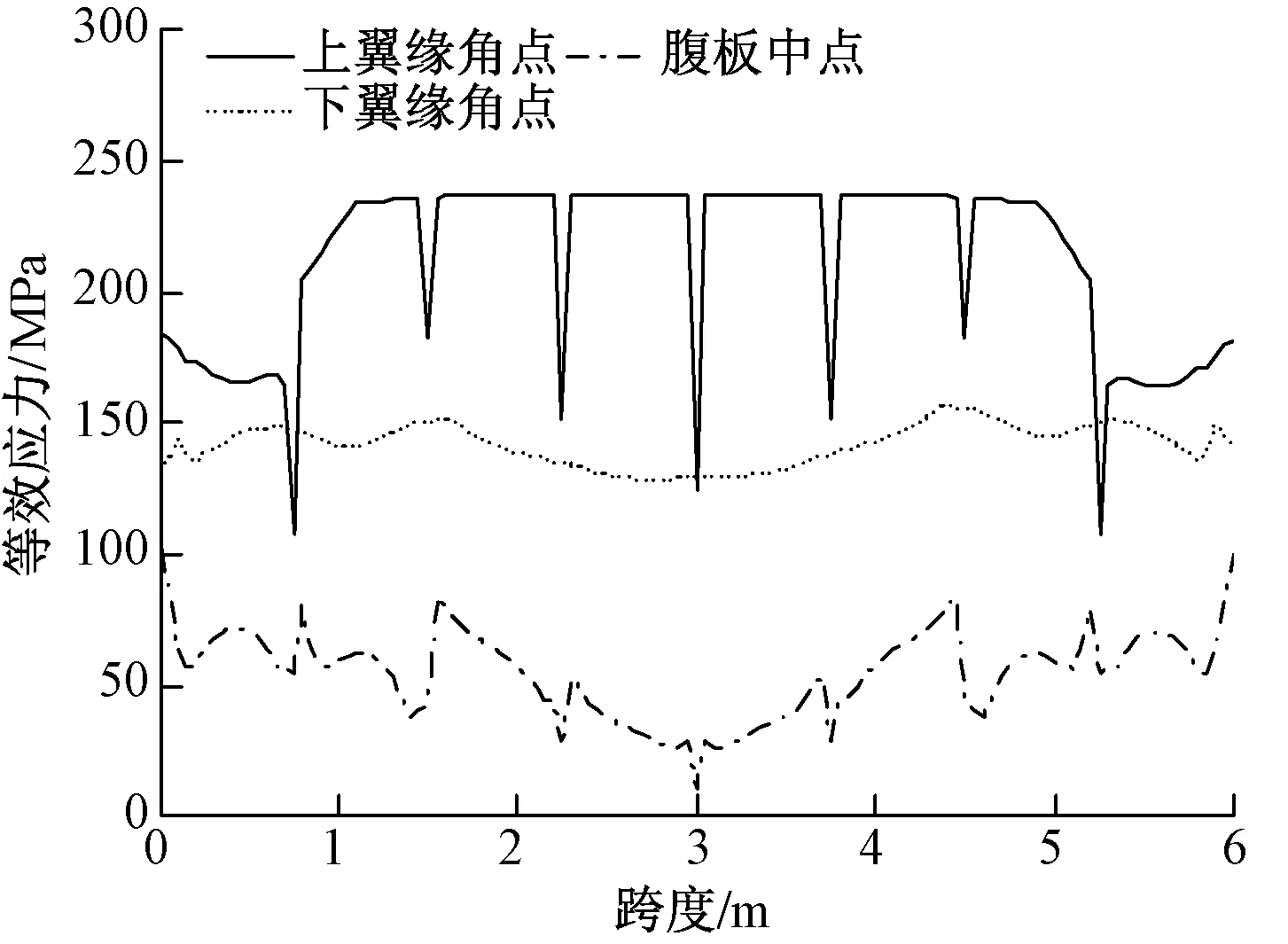
图6 原吊车梁屈服状态

3.2 拟定加固方案

原吊车梁分析结果显示，在吊车荷载增大较多的情况下，原吊车梁的竖向、横向刚度均不满足要求。增大吊车梁刚度可采用的方法有：缩短跨度、增加梁高、加厚腹板、加宽翼缘等。结合国内外吊车梁加固研究成果，并考虑到吊车梁实际工作环境特点，初步拟定3种加固方案，如表3所示。

吊车梁不同加固方案 表3

4 吊车梁加固方案分析

4.1 各方案分析结果

(1)方案1

在1/3，2/3跨采用钢斜撑支承加固原吊车梁，将原6m简支梁转变为跨度2m的3跨连续梁。

吊车梁最大竖向弯矩65.562kN·m，最大横向弯矩3.073kN·m，最大剪力163.91kN。根据式(3)，吊车梁受弯强度验算值79.97MPa，受剪强度验算值66.04MPa，β=0.047时，竖向临界荷载321.49kN。吊车梁强度和稳定性满足设计规范要求。

选取弯矩最不利工况(图7)进行有限元分析。结果显示，加载至设计荷载的95.48%，即竖向临界荷载为156.5kN时，吊车梁发生屈曲失稳。可见方案1加固方式无法满足需求，也进一步证明对于无制动结构钢吊车梁而言，仅考虑双向弯曲，忽略扭转效应不够安全。

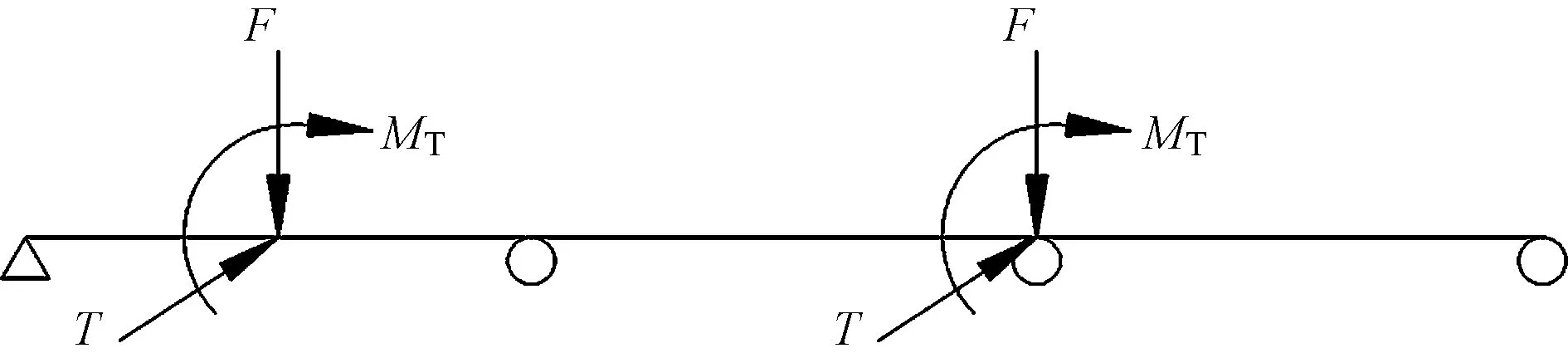
图7 6m连续吊车梁最不利受力简图

图8为方案1加固后吊车梁屈服状态下截面各点位沿纵向的等效应力。可以看出，采用方案1加固，吊车梁在钢斜撑支承位置(下翼缘)以及上翼缘加载位置都达到屈服状态。吊车梁在屈服状态下，最大竖向位移降至17.56mm，降幅较大；最大横向位移仍有48.81mm，降幅较小。方案1加固方式虽然提高了吊车梁竖向刚度，但对横向刚度提高不大。

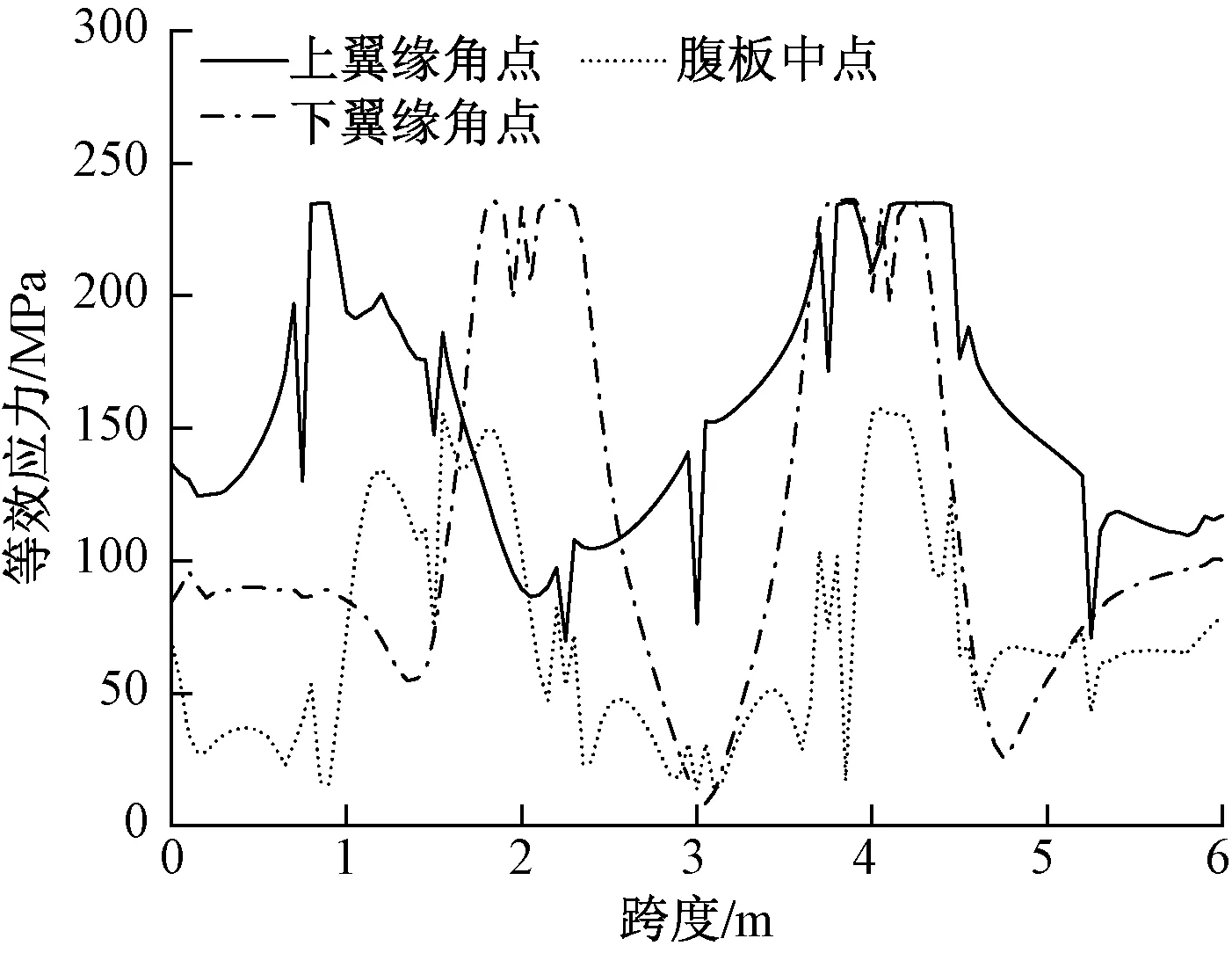
图8 方案1吊车梁屈服状态

(2)方案2

原吊车梁分析显示，吊车梁上翼缘在荷载作用下首先进入屈服状态，因此可采用加宽上翼缘来加强翼缘。但仅加强翼缘难以满足承载力要求，进一步采取增大梁高来提高吊车梁的抗弯性能。由于厂房上方净空尺寸限制，考虑将原吊车梁向下增高，即加固成“鱼腹形”钢吊车梁(图9(a))。

上翼缘两侧各加宽65mm，加宽至329mm，翼缘宽厚比为14.64<15，可满足局部稳定要求。根据式(3)，钢梁向下加高100mm，加固部分腹板厚12mm，加固部分翼缘厚14mm，吊车梁受弯强度验算值152.21MPa，受剪强度验算值78.97MPa，β=0.047时，即竖向临界荷载为207.5kN。吊车梁强度和稳定性满足设计规范要求。

原横向加劲肋与下翼缘之间存在50mm空隙，梁加高后，增设钢板将原横向加劲肋接长填补该空隙，同时在下翼缘以下增设6mm厚钢板使横向加劲肋向下延长至距离新翼缘50mm处。

弯矩最不利工况与原吊车梁一致。根据分析结果，提取截面各点位应力结果作为判别加固效果的依据(图9(a))。其中位置1为对接焊缝，位置2为上翼缘角点，位置3和位置4为角焊缝，位置5为下翼缘角点。图9(b)～(f)为方案2加固后吊车梁截面各点位沿纵向的应力计算结果。结果显示，钢梁向下加高100mm，在吊车荷载作用下，位置2正应力值达235MPa，跨中上翼缘区域已非常接近屈曲状态。

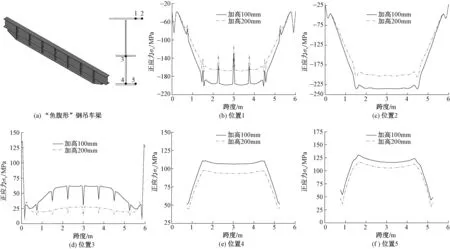
图9 方案2加固后吊车梁及其横截面不同位置应力

将钢梁高度进一步增加，当加高至200mm时，位置1最大正应力170MPa；位置2最大正力205MPa；位置3最大正应力135MPa，最大剪应力30MPa；位置4最大正应力98MPa，位置5最大正应力116.9MPa，强度满足要求。此时吊车梁最大竖向位移8.27mm，最大横向位移6.29mm，刚度满足要求。

(3)方案3

方案3是在原吊车梁上下翼缘之间焊接通长的两片平行于腹板的钢板(图10)，将截面封闭成箱。根据式(3)，采用8mm厚平行板，吊车梁受弯强度验算值145.38MPa，受剪强度验算值78.97MPa，强度和稳定性满足规范要求。

图10 加焊平行板的钢吊车梁

弯矩最不利工况与原吊车梁一致。根据分析结果，提取截面各点位(图10)应力结果作为判别加固效果的依据，其中位置2为角焊缝。结果显示(图11)，吊车梁具有较高的强度，没出现屈曲失稳，但位置2最大正应力180.3MPa>160MPa，不满足要求。

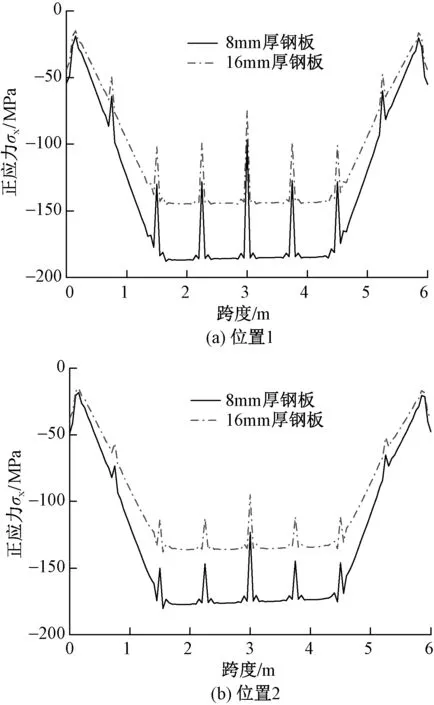
图11 方案3加固后吊车梁横截面不同位置应力

将平行板厚度增至16mm，位置2最大正应力138MPa<160MPa，位置1最大正应力145.27MPa，强度满足要求。此时吊车梁最大竖向位移11.6mm，最大横向位移1.05mm，刚度满足要求。

4.2 有限元分析结果与规范比较

实际无制动结构钢吊车梁是双向弯曲和扭转的联合受力。而关于无制动结构钢吊车梁在双向弯曲和扭转作用下的强度、稳定性计算问题，现行钢标没有相应条款，也没有相应设计方法。现行《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[10](简称薄规)，给出了冷弯薄壁型钢结构在双向弯曲和扭转作用下的强度、稳定性计算式为：

(4)

式中：B为与所取弯矩同一截面的双力矩；Wω为毛截面扇形模量。

表4为不同加固措施下吊车梁有限元分析结果与按照式(3)，(4)计算结果的比较。由表4可知：1)方案2双力矩引起的翼缘正应力值较大，造成薄标解(式(4))和钢标解(式(3))差异大。虽然薄规解考虑了双力矩影响，但与ANSYS解仍有一定偏差。主要原因是方案2这类水平非对称开口截面抗扭转刚度小，在弯扭耦合作用下，因翘曲产生的正应力在截面上分布不均匀，会产生二次弯矩，进而产生二次扭矩。稳定性方面薄规解偏于安全。2)方案3截面抗扭刚度大。强度方面，双力矩引起正应力值较小，薄规解和钢标解差异较小，与ANSYS解偏差较小。方案3钢梁截面属于双对称闭口截面，按照规范计算的钢梁强度偏大，两个规范的强度结果均偏安全。因此对于方案3，可以忽略双力矩的影响。这也进一步证明，双对称闭口截面可采用梁单元来简化分析。

不同加固措施下吊车梁有限元分析结果与规范解比较 表4

4.3 加固方案探讨

根据上述分析结果，采用方案2(向下加高200mm)和方案3(16mm平行板)对吊车梁加固后，吊车梁均能满足新的工作需求。

对比方案2(向下加高200mm)和方案3(16mm平行板)，方案2所需的钢材量(292.77kg)要比方案3(563.69kg)少，且方案2的焊接工作量与方案3大致相等。考虑到施工的便利性及经济性，推荐采用方案2(向下加高200mm)对原吊车梁进行加固，即上翼缘两侧各加宽65mm，钢梁向下加高200mm，加固部分腹板厚度为12mm，加固部分翼缘厚度为 14mm。

5 结论

(1)通过对比有限元分析结果和试验结果，证明本文所采用的有限元模型能够较精确地模拟无制动结构钢吊车梁在弹性或弹塑性阶段的力学性能。

(2)原吊车梁采用方案2(向下加高200mm)加固后，能满足新工作需求。强度方面，方案2这类水平非对称开口截面在弯扭耦合作用下的二次应力效应，造成与薄规解的差异。稳定性方面，薄规解偏于安全。对于方案2这类水平非对称开口截面，双力矩引起的正应力不能忽视。

(3)采用方案3(16mm平行板)加固吊车梁能满足工作需求。强度和稳定性方面，规范解均偏于安全。对于方案3这类双对称闭口截面，双力矩引起的正应力较小，可忽略，这类梁可采用梁单元来简化计算。

(4)对比不同加固方案，推荐采用方案2，该措施能够显著提高吊车梁的力学性能，且施工便利，经济性好。