单形的几何稳定性研究

孙玉婷，王 文，杨世国

（1.安徽文达信息工程学院通识教育学院，安徽合肥 231201；2.合肥师范学院数学与统计学院，安徽 合肥 230601；3.安徽新华学院国际教育学院，安徽合肥 230088)

0 引言

凸体几何发源于上世纪初的现代几何学科，随着国内外优秀数学家对凸体几何研究的深入，到上世纪末凸体几何研究得到蓬勃发展.凸体几何的理论和方法广泛的应用于体视学（stereology）、仿晶学（sryslallography）和固态物理学等领域[1].尤其对C60的研究显示了凸体几何在化学研究中的作用，从而让C60在化工、建筑等其他领域得到广泛应用[2-3].

单形是凸体几何的主要研究对象，而本文主要研究其不等式的稳定性.单形不等式的稳定性最早由MINKOWSKI 提出，是指在一些含有等号的几何不等式中，当其中的几何体为某种特殊几何体或几何体相似时取等号.现假设某几何体使得不等式与相等时相差很小，那么此时几何体与取等号的特殊几何体的“偏差”也很小，则称此几何不等式是稳定的，否则称此几何不等式是不稳定的.由于它的支撑函数或向径函数的表达式很难找到，使得其几何不等式的稳定性研究十分困难.文献[4-5]证明了Veljan-Korchmaros 不等式是稳定的，并提出了单形的“偏正度量”概念：

设n维单形Ω的棱长为是以aˉ为棱长的n维单形，则单形Ω的“偏正度量”为当且仅当Ω为正则单形）.

文献[6]给出了单形不等式更强的稳定性版本.

1 主要结果

并推广了[7]中切点单形不等式，得到推广式

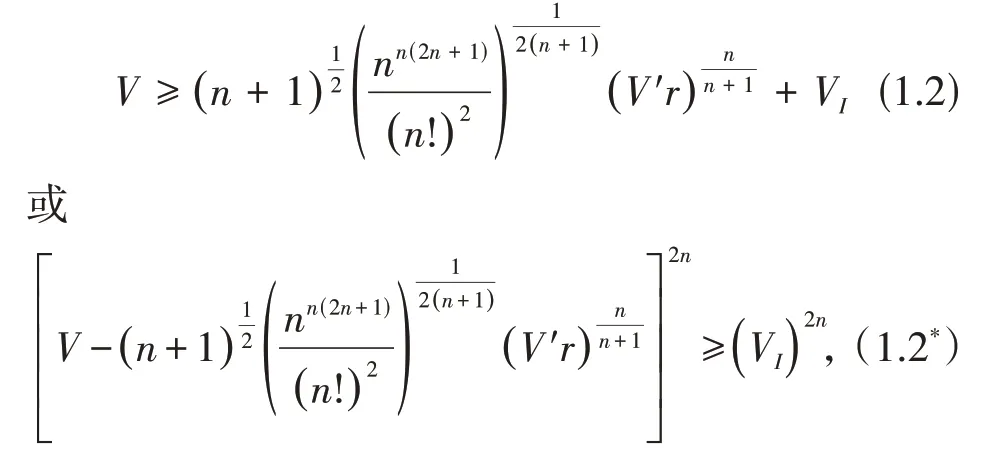
当Ω为正则单形时，（1.2）和（1.2*）中等号成立.

本文将证明（1.1）与（1.2）是稳定的，并给出他们的稳定性版本，并推广不等式（1.1）与（1.2），而本文其中一个结论实质上是比文献[1]有更强的稳定性.

定理1.1n维单形Ω有

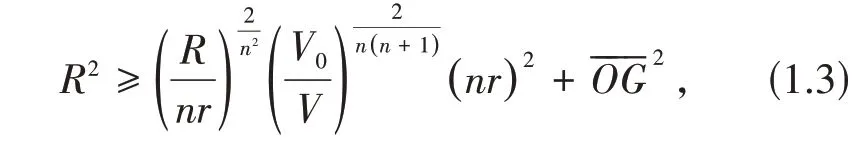
且当且仅当Ω为正则单形等号成立.

或有不等式(1.1*)的一个稳定性版本

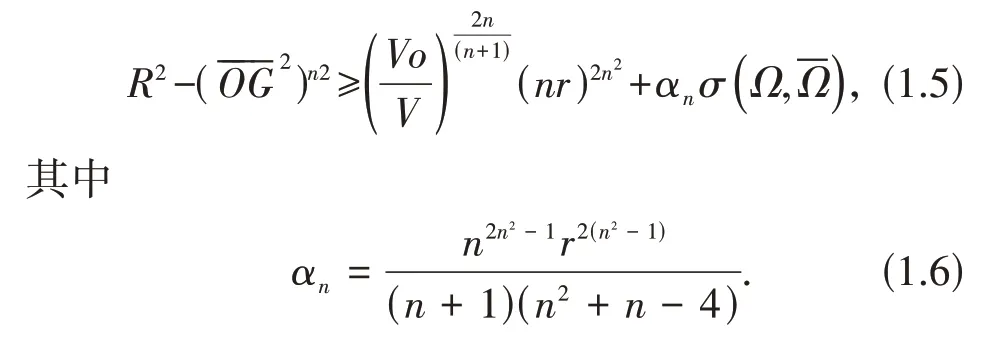
当且仅当Ω为正则单形，(1.5)式中等号成立.

定理1.3n维单形Ω有

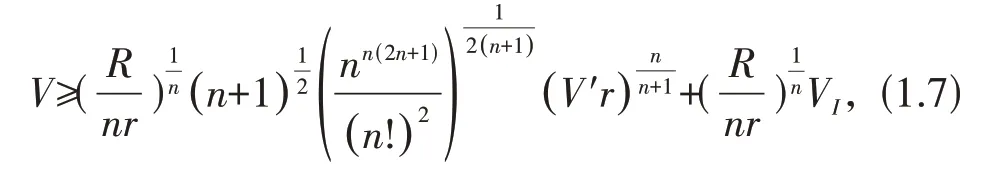
且当Ω为正则单形时等号成立.

定理1.4设是n维单形的偏正度量，对任意的ε＞0，当

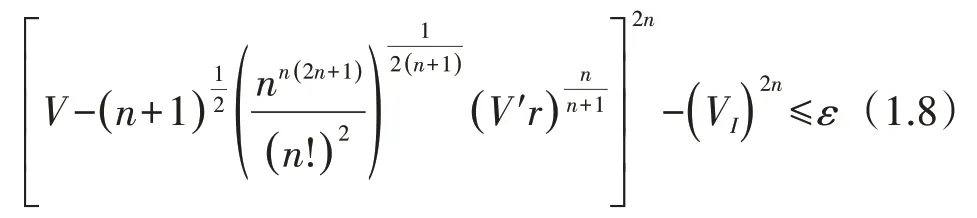
时，则有

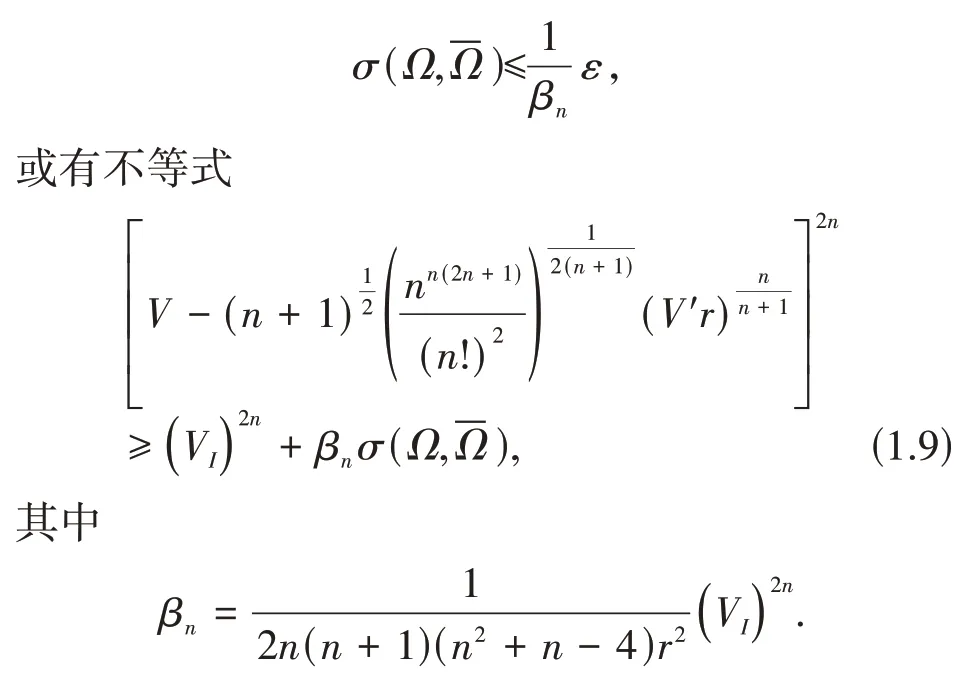
当且仅当Ω为正则单形，(1.9)式中等号成立.

2 主要结果证明

引理2.1[4]设n维单形Ω，则

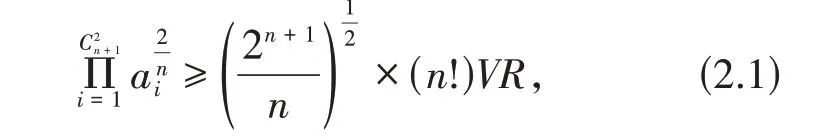
且当Ω为正则单形时等号成立.

引理2.2[5]设n维单形Ω，则

且当Ω为正则单形时等号成立.

引理2.3[9]设n维单形Ω，则

且当Ω为正则单形时等号成立.

引理2.4[10]设x≥1,0 ＜β≤1，有

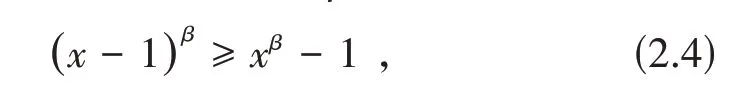
当β=1 时，（2.4）式为恒等式；当0＜β＜1 时，(2.4)式等号成立当且仅当x=1.

引理2.5[10]设n维单形Ω，有

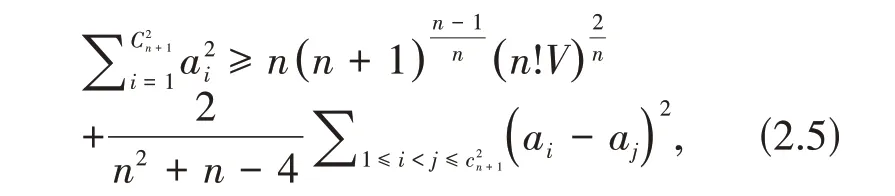
且当Ω为正则单形时等号成立.

引理2.6设n维单形Ω，则

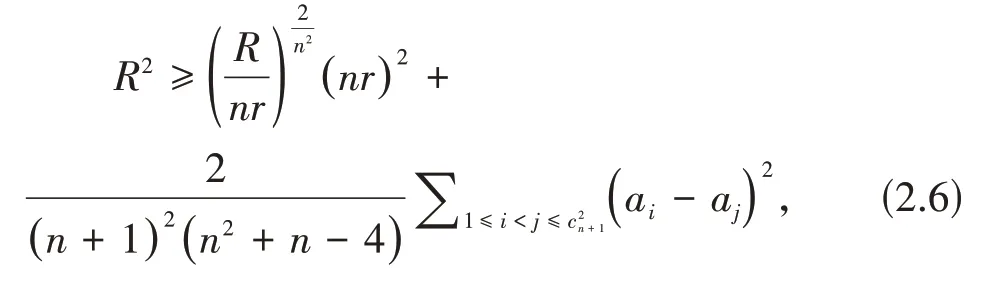
且当Ω为正则单形时等号成立.

证明利用文献[9]中不等式

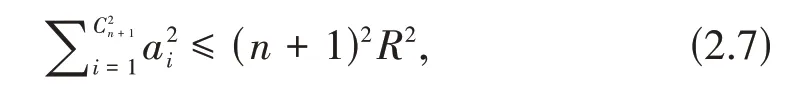
当Ω重心与外心重合时等号成立，由(2.5)和(2.7)得

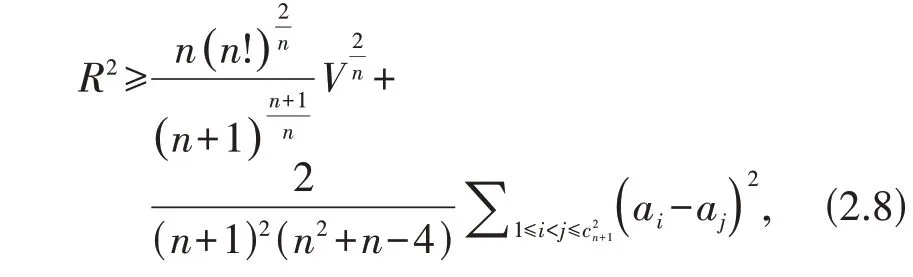
由(2.8)和(2.2)引理得证.

定理1.1的证明由[11]中结果

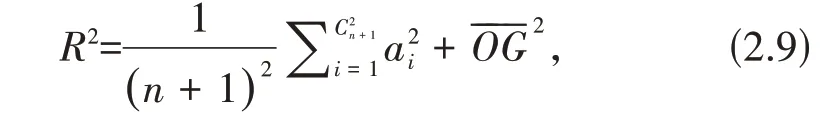
并利用算术几何平均不等式及(2.1)得

由(2.9)和(2.10)得

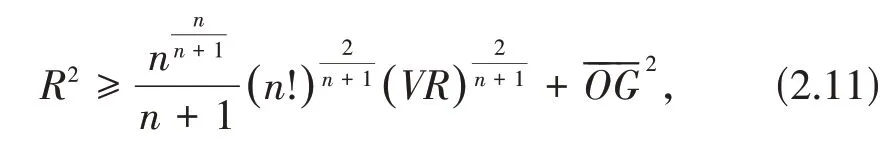
且当Ω为正则单形时等号成立.

利用引理2.3有

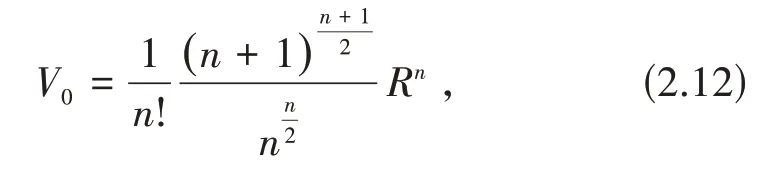
由(2.11)和(2.12)得

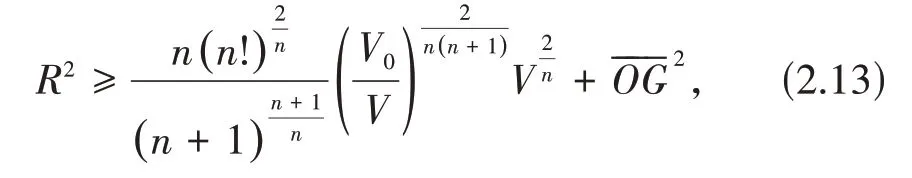
由(2.13)和(2.2)得

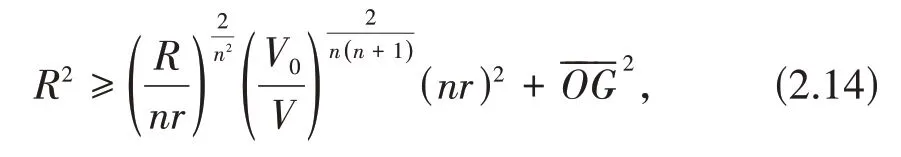
且当Ω为正则单形时(2.14)式等号成立.

故定理1.1成立.

定理1.2的证明(2.14)式可改写成

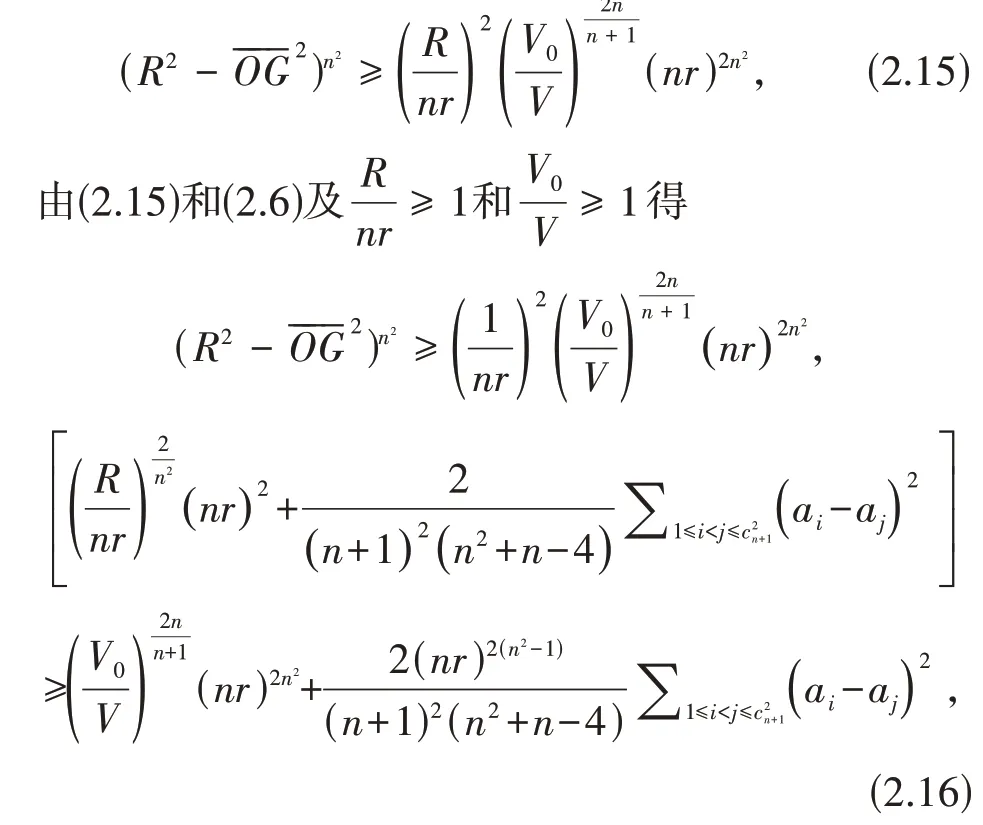
注意到代数恒等式

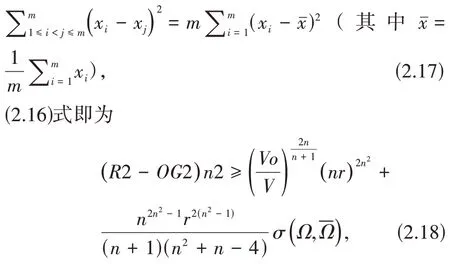
Ω为正则单形时(2.18)等号成立.

故定理1.2成立.

定理1.3 的证明由于切点单形Ω′得外接球半径为γ,外心为I,将不等式(2.11)应用于切点单形Ω′,有

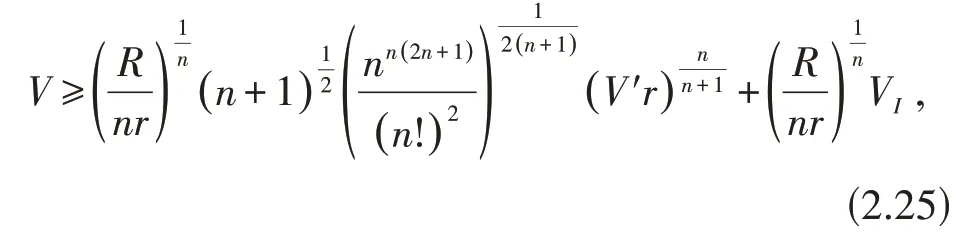
当Ω为正则单形时等号成立.

从而定理1.3成立.

且当Ω为正则单形时等号成立.

利用文献[5]中引理3.11有

且当Ω为正则单形时等号成立.

由(2.26)和(2.27)得

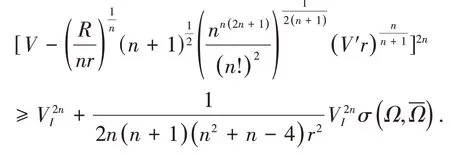
从而定理1.4成立.

3 结语

本文通过研究欧氏空间正则单形与一般单形的偏差估计，为后期研究非欧空间如球面空间、双曲空间等单形的稳定性奠定了一定的基础；同时由于单形是特殊的凸体，单形的稳定性研究为一般凸体稳定性研究提供了一定的启发.