基于VMD-GPR的锂离子电池健康状态预测研究

曾 镖，徐位君，谈 宸

（荆楚理工学院电子信息工程学院，湖北 荆门 448000）

0 引言

锂离子电池具有能量密度大、输出功率高、无污染、无记忆效应、自放电小等优点，已成为当前新能源汽车主要应用的电池类型。而电池的健康与否，在很大程度上决定了电动汽车性能的优劣。

目前，已有人工智能相关方法应用于锂离子电池健康状态预测。例如依靠神经网络等人工智能方法对电池的荷电状态进行预测[1]；通过改进的各类优化算法对建立预测模型进行超参数寻优，提升模型的预测准确度[2]；改变模型输入的参数，对各类影响因素进行相关性分析，选取合适的因素作为训练输入[3]。但都未分开考虑复杂运行环境给锂离子电池带来的多方影响[4]。

本文将采集到的锂离子电池的电压和内阻作为模型输入，通过锂离子电池的容量来表征其健康状态并作为模型输出，构建基于VMD-GPR的铅酸锂离子电池的健康状态预测模型。通过分解将各类影响因素分开，对各分量分别构建预测模型，最后通过集成算法得到最终的预测模型。

1 变分模态分解

变 分 模 态 分 解 （Variational Mode Decomposition，VMD）算法通过自适应迭代将原信号分解成N个本征模态函数（Intrinsic Mode Function，IMF），在满足各IMF累加等于原始信号f（t）的条件下，使各IMF带宽之和最小[5]。其具体的求解步骤如下所述：

1）将初始信号f（t）分解为N个分量相应的约束变分方程为：

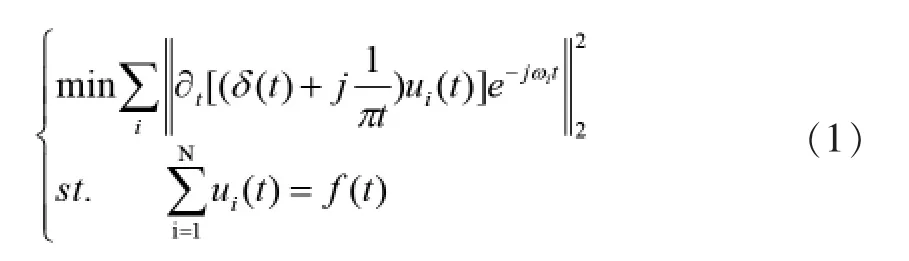
其中：ui(t)、wi分别为分解得到的第i个本征模态分量及其中心频率，б(t)为狄拉克函数。

2）引入拉格朗日乘子，把约束变分问题转化为非约束变分问题。如式（2）所示：

其中：λ为拉格朗日乘子，α为二次惩罚因子，保证了重构信号的精度。

3）逐步求解各分量带宽uk和中心频率ωk。如式（3）、式（4）所示：

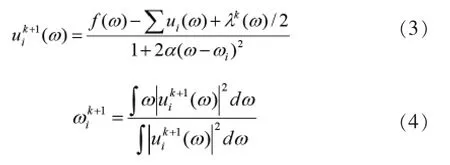
其中：u(ω)、f(ω)为模态分量和初始信号经过傅里叶等距变换的结果；k为迭代次数；i为模态分量编号。

4）更新λk直至达到迭代终止条件。更新公式如式（5）所示：

若式（6）成立，则停止迭代并输出分解后的分量集合{ui(t)}，若不成立则转入步骤3）重复以上步骤。

2 基于VMD-GPR的锂离子电池健康状态预测模型

高斯过程(GaussianProcess，GP)对于处理非线性、小样本的数据预测问题有不错的适应性。在假设数据样本符合正态分布以及联合正态分布的基础上将数据分组为训练样本和待预测数据，通过逐步计算训练样本和待预测数据样本的联合概率分布、先验概率分布，从而最终得到预测数据的高斯分布情况。

由于锂离子电池的内阻和端电压方便测取，且内阻与电池的老化程度密切相关，因此结合内阻和端电压作为模型的输入，利用锂离子电池的剩余容量表征其健康状态SOH并作为模型的输出。通过VMD将各原始数据分解为固定个数分量，并一一对应整理为新的子训练集，分别训练GPR模型。该预测模型的框架如图1所示。

图1 锂离子电池健康状态预测模型框架

3 算例分析

本文选用的锂离子电池规格为标定电压48V、额定容量300Ah，并在MATLAB2016a软件平台进行仿真。预测结果如图2、图3、图4所示，其中GPR、VMD-GPR曲线分别代表使用GPR模型和改进后的模型，误差统计结果如表1所示。

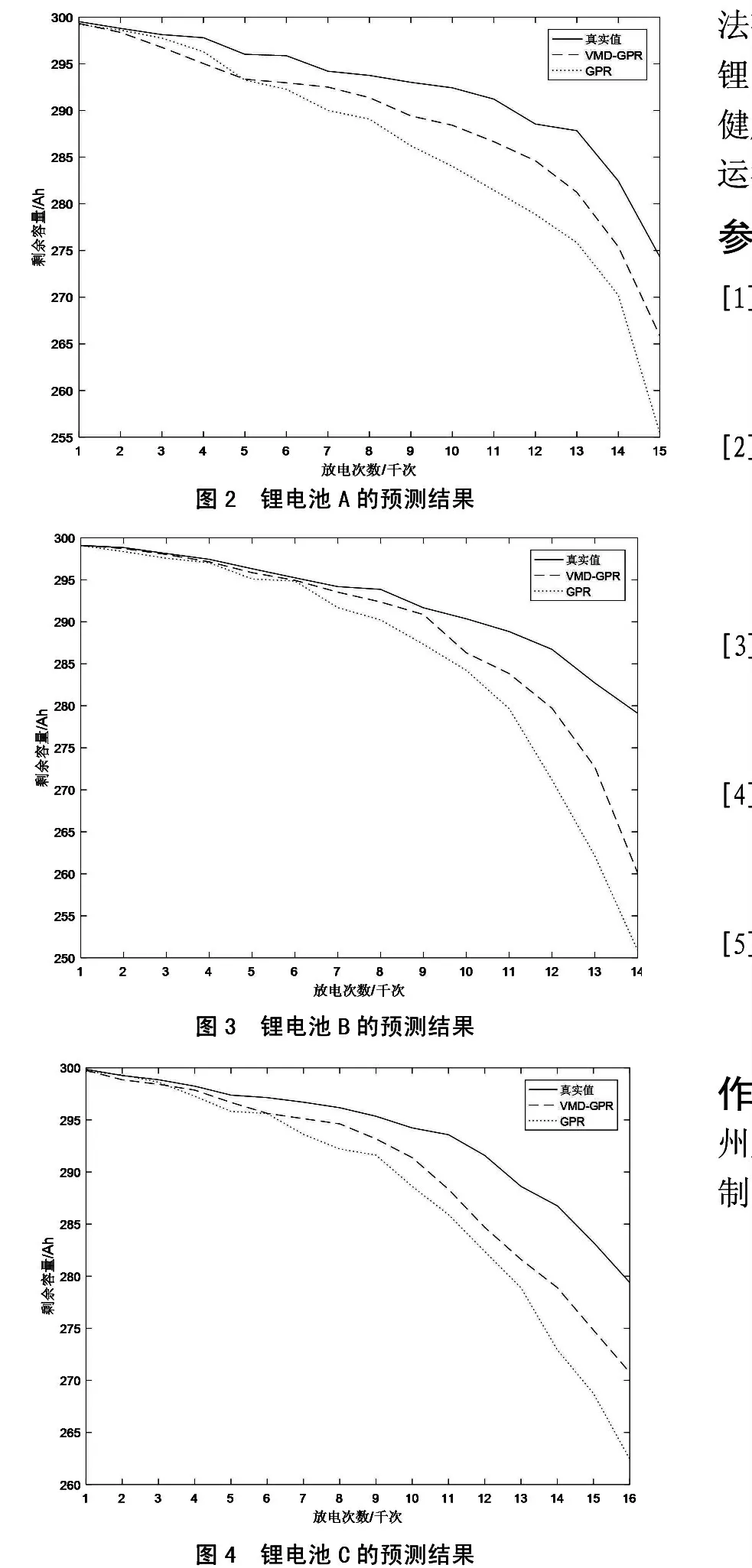
图2 锂电池A的预测结果

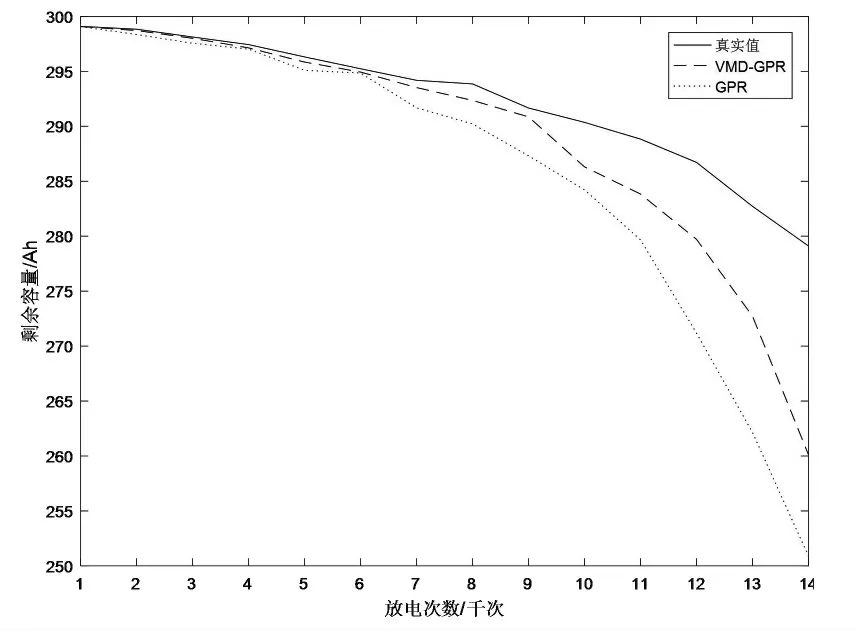
图3 锂电池B的预测结果

图4 锂电池C的预测结果

表1 各模型预测误差（RMSE）对比

由表1中的误差可知，VMD-GPR模型由于采用上述方法进行了改进，该模型对不同变电站的预测效果基本一致且准确率较高。而在GPR模型中，预测效果在不同变电站中并不稳定而且误差较大。

4 结论

本文所提出基于VMD-GPR锂离子电池的健康状态预测模型准确率较传统方法有大幅提高，该模型能在考虑不同工况对锂电池健康状态的影响，并准确估算锂电池健康状态，为锂离子电池的日常维护和稳定运行提供有效支撑。