压滤机张紧辊筒壁厚的可靠性设计*
2021-03-12张嘉易
彭 程,张嘉易
(沈阳理工大学机械工程学院,辽宁 沈阳 110159)
0 引言
带式压滤机作为一种自动化过滤脱水设备,因为其过滤脱水效果显著,受到了相关行业的普遍欢迎[1]。目前广泛应用于造纸、食品加工、采矿洗煤、环境保护等行业。张紧装置是带式压滤机上较为重要的一个部件[2]。其主要作用是提供一个合适的张紧力使滤带始终处于张紧状态,确保带式压滤机具有良好的过滤效果。
带式压滤机张紧装置包括张紧机构和张紧辊筒两部分。其中张紧辊筒部分是本文研究的主要重点,张紧辊筒装配图如图1所示,其包括张紧辊轴头、张紧辊筒、透盖等多个零件构成。因为张紧辊筒的性能直接影响带式压滤机的工作状态,虽然辊筒设计在安装和运行上做了很多考虑,但在设计方面还有许多关键结构有待于进一步优化设计,鉴于压滤机上辊筒的重要性,所以本文针对带式压滤机的张紧辊筒的壁厚进行机械可靠性的设计。通过常规设计方法与可靠性设计计算方法的对比分析。选择更加优化的设计参数。
本文主要解决以下问题:疲劳强度下带式压滤机张紧辊筒壁厚的可靠性优化设计方法;辊筒壁厚常规设计方法与可靠性设计方法的对比分析。
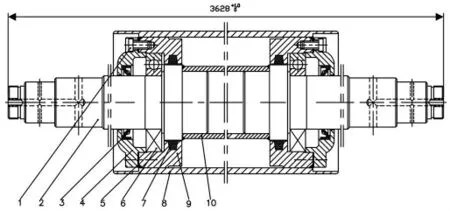
图1 张紧辊筒装配图
1 机械零件可靠性优化设计
在机械结构和零件设计方面,可靠性设计方法目前得到了广泛的应用和研究[3-4]。England等人阐述了评估结构对不可预见事件脆弱性的重要性,并探讨了不可预见事件的性质。论述了一种结构易损性理论,以确定最脆弱的失效事件序列。通过一种新的潜在危险性测量方法,研究了损伤在结构中传播的可能性。提出了能够找出桁架结构的薄弱部位的可靠性方法[5]。胡晓义等人针对复杂系统的可靠性分析热点问题进行了研究。阐述了航空机载系统的逻辑功能、设计架构以及容错方法逐渐复杂,采用人工推理的可靠性分析方法已经不能满足需求,提出模型驱动将成为可靠性设计的重要方法[6]。莫冰等人将可靠性设计方法应用于精密机械结构设计,对机械结构的精度程度、可靠程度与安全性进行了深入研究。应用应力——强度干涉模型,阐述了精密结构的可靠性设计要点,并对椭偏仪变角机构的转接轴展开了可靠性详细设计,在保证精密仪器使用要求的前提下,使结构具有高的可靠性指标[7]。
1.1 应力——强度干涉模型
常规设计是按经验安全系数为依据来判定零件强度是否达到要求,这种方法存在一定的保守性和偏差,没有考虑零件在长期使用中的失效概率。图2a所示为应力强度理论干涉模型曲线图。常规设计往往偏重于确保零件在出厂时强度大于应力的裕量,没能利用统计概率的方法定量计算零件在长期工作环境下材料强度的衰减情况。而可靠性设计方法充分利用材料在长期循环载荷下的强度衰减规律曲线,采用随机变量的统计概率计算方法,合理计算出满足规定可靠度下的机械零件关键结构尺寸。
1.2 联结方程
根据应力——强度干涉模型计算可靠度原理如下。
由于应力小于强度时不发生失效,所以应力小于强度的全部概率值就是可靠度R,用概率公式表示如下。

式中:σ—代表应力,δ—代表强度。如图2b所示,其中令:f(σ)为应力分布概率密度函数,g(δ)为强度分布概率密度函数,则强度大于应力的概率,即可靠度计算的一般公式表示如下[8]。

对于机械零件的应力和强度来说都受到多种因素的影响,如载荷、零件表面质量、加工精度、应力集中、尺寸等。因此,零件的应力和强度一般可看作正态分布,根据概率论相关知识可推出强度大于应力的计算公式如下。
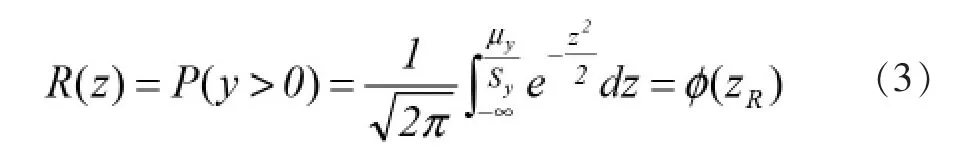
其中:y=δ-σ,于是得到机械可靠性设计中的重要公式——联结方程(即(3)式的积分上限)。

式中:ZR为可靠度指数,在根据统计概率方法计算出强度分布N(μδ,Sδ)和应力分布N(μσ,Sσ)后,将应力和强度的均值和标准差带入联结方程(4)后查标准正态表即可求得可靠度R,或由给定的R值求解危险截面尺寸。

图2 应力——强度干涉模型
2 张紧辊筒壁厚的传统计算方法
传统设计方法是以安全系数为依据,按机械手册中的经验公式[9],不考虑载荷与强度的分布情况,将设计变量与参数看作常量(一般为均值),按常规计算公式进行计算。
本文张紧辊筒选择外径为180mm的无缝钢管,材料为45号钢,查附表可得疲劳极限σ-1=279.95MPa[8],我国机械设计手册规定安全系数的取值根据材料不同及载荷的情况来确定,范围在1.3~2.5之间,这里辊筒载荷受煤泥等压滤物料薄厚变化张紧力波动影响(6%的波动比率),是动载荷,因此取安全系数为[ζ]=1.7。经辊筒受力分析,得辊筒危险截面弯矩均值为M=38 215 520N·mm。按压滤机结构要求,辊筒大径D=180mm,半径R=90mm。辊筒可看作受对称循环弯矩作用σm=0,最大弯曲应力发生在截面的底面和顶面,根据机械设计手册方法[9]可以得到下面安全系数公式。

得:

式(6)中:Kσ—代表弯曲应力集中系数,由于最大发生弯矩在辊筒中心,内外表面较为光滑,因此取Kσ=1,β-代表表面质量系数=加工系数β1×强化系数β2;εσ—代表尺寸系数。辊筒须用无缝钢管关键尺寸切削加工保证,由此查表得:β=0.793 3×1.6=1.269,εσ=0.802 5。由于是无限寿命下的疲劳强度计算,查表得45号钢的对称疲劳极限为:σ-1=279.59MPa。这里只有弯曲应力作用,因此应力幅为。

式中:σW—弯曲应力MPa;M—弯矩N·mm;C—截面中轴到辊筒外表面的距离mm;I—截面对中性轴的惯性矩mm4。
根据惯性矩公式有:

其中:α=r/R,r为辊筒内径,R为辊筒外径。令A=R3(1-a4)代入公式(7),利用公式(6)得到如下计算过程。

由上面算式得A≥290 516.308mm3,α≥0.881,r≥79.259mm,所以壁厚H最小值为H=R-r=10.741mm。
3 带式压滤机张紧辊筒壁厚的可靠性优化设计
可靠性设计方法是将所有的设计变量和参数都看作随机变量。按统计概率的计算方法计算出强度和应力的分布参数,主要是强度和应力的均值和标准差,然后带入联结方程求取未知参数。本文将α作为未知参数,按常用机械结构可靠度要求的可靠度指标R=99%的情况下[8],计算辊筒中间弯矩最大处的α值,从而确定辊筒壁厚H。具体计算方法如下。
零件发生强度破坏而失效的概率:F=1-R=0.01。由F值查标准正态函数分布表[8]得可靠性指数ZR=2.33。危险截面弯矩的均值为M=38 215 520N·mm,根据弯矩6%的波动比率,按3倍标准差原则计算弯矩标准差SM,变差系数为CM。

根据第四强度理论,合成应力为σe。

该辊筒由于是对称循环载荷,弯曲应力幅值(σW)a≠0;弯曲应力均值(σW)M=0,扭剪应力等于零。因此有,可以计算出合成应力为。由于辊筒加工尺寸误差与载荷变化比率相比可忽略不计,即可认为R的变差系数CR< 根据对称应力循环特性r=-1,其等寿命疲劳极限图中应力σe与横坐标轴的夹角θ=90°。查表可知当r=-1,N=107时σr=,疲 劳 极 限 标 准 差Sσ-1=8.17MPa,Cσ-1=0.029。 辊筒在计算截面处的疲劳极限为: 求出辊筒的疲劳极限应力均值: 将有关数值代入联结方程(4)有: 将式子两边同时平方并整理可以得到下式: 方程求解得到A1=142 492.683和A2=212 159.858。代入(12)式A2合理,由A=R3(1-a4)无缝管外径R为90mm,求得α=0.918,r=82.585mm。壁厚H=R-r=7.415mm。 根据机械手册安全系数选取范围[ζ]=1.3~2.5,利用常规设计方法计算辊筒壁厚结果如表1所示。 表1 不同安全系数的辊筒壁厚 从表1中可见即使安全系数最小时[ζ]=1.3,辊筒壁厚H=7.818仍然有较小的余量,这说明传统基于安全系数的计算方法偏于保守。 常规设计方法带式压滤机张紧辊筒壁厚最小应为10.741mm,运用可靠性设计在疲劳强度下计算出的张紧辊筒最小壁厚为7.415mm。通过计算出的结果对比,应用可靠性设计计算出的壁厚更精确,计算出的壁厚明显减小,这样在张紧辊筒的规格选择上能够更直观的表现出最佳方案,起到了优化设计的作用。由于常规算法没有考虑到各种变量的随机性,只是按照安全系数来计算,这样计算出的结果误差较大,导致材料浪费。应用可靠性设计计算出的材料重量减轻,减少材料浪费,降低辊筒生产成本,提高压滤机生产经济效益。


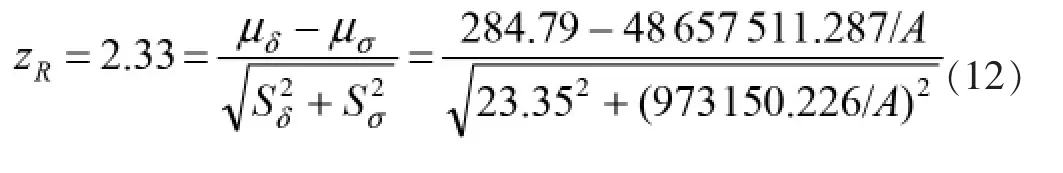

4 可靠性与常规设计对比

5 结论
