基于热-结构耦合分析的液化石油气储罐失效预警判定*

2021-03-11李伟东陈明哲

中国安全生产科学技术 2021年2期

李伟东，陈明哲，李玉，韩帅

(1.中国人民警察大学，河北廊坊 065000； 2.东营市消防救援支队，山东东营 257000； 3.德州市消防救援支队，山东德州 253000)

0 引言

据统计，2019年全国液化石油气(Liquefied Petroleum Gas,LPG)总产量约4 135.7万t，比2018年累计增长10.9%[1]。作为新型燃料，LPG被广泛使用[2],同时LPG储罐火灾、爆炸等事故逐渐增多，给人民生命及财产安全造成巨大危害。

火灾环境下液化气储罐热力学响应一直是石油化工领域热点问题：Giordano等[3-4]通过实验和数值分析相结合的方法,确定LPG容器临界爆炸条件，在二维CFD模拟基础上,探索森林火灾导致LPG储罐失效条件;Chukwugozie等[5]采用数值模拟方法，在ANSYS中研究瞬态边界温度对LPG储罐结构的影响，并通过304不锈钢材料标准曲线对应力-应变曲线进行验证;Mihai等[6]以LPG储罐质量最小为目标函数，通过有限元数值模拟计算出储罐最佳形状与尺寸，并进行验证;黄拴雷等[7]采用ALOHA软件对LPG储罐泄漏事故进行研究，并基于LPG泄漏量、空气湿度、风速、储存温度等爆炸事故后果影响因素进行数值模拟;邢志祥等[8]根据LPG储罐热响应规律建立数学模型，开发用于预测储罐温度与压力随时间的变化情况的数值模拟软件，并在不同火灾类型下对储罐的力学响应进行实验;Zhao[9]将Legendre小波函数与传统有限元相结合，建立LPG储罐在火灾下的温度-压力-应力耦合模型，有效分析了各因素对LPG储罐火灾耦合场变化规律的影响;王学岐等[10]与张瑞华[11]分别运用FLACS软件与多相混合数学模型对液化气球罐的泄漏扩散、爆炸事故后果进行数值模拟分析，从不同角度与层面分析了泄漏爆炸影响因素;任婧杰[12]搭建立式圆柱形LPG储罐热响应实验平台，对储罐罐壁与内部介质的传热现象进行数学描述，发现储罐受喷射火时的压力、壁温和介质升温速度均高于池火;巩建鸣等[13]利用一系列LPG储罐在火场下的热响应数学模型，计算不同容积、不同形状压力容器在受热时的动态过程，得出球罐罐壁和内部介质的温度场随时间变化规律，并预测储罐的破裂时间;江伟等[14]利用有限元分析软件对LPG储罐遭受火灾威胁时，对高温与内压作用下导致的储罐破裂变形过程进行数值模拟，并得出储罐罐壁不同位置应力分布;米静[15]利用ANSYS软件对火灾环境中LPG球罐采取三维有限元分析，研究温度与静力载荷共同作用下，不同时间节点球罐应力及应变分布，探讨球罐失效机理。

针对LPG储罐数值模拟、实验及事故机理的研究较多，但有关储罐失效预警模型方面研究较少。在进行灭火时，消防人员只能凭借主观经验判断火场中LPG储罐是否达到临界失效点。若撤退不及时，LPG储罐爆炸将危及消防人员生命安全；若过早撤退，容易失去扑救火灾最佳时机，后果可能更严重。通过数值模拟研究储罐在池火灾下热力学响应规律，分析LPG储罐失效条件，建立LPG储罐失效预警系统，为消防救援提供数据参考。

1 数学模型

1.1 池火灾模型

假设池火灾全包围球形储罐，如图1所示，火焰内任意微元体dV对储罐壁上任意点P微元dA的辐射热如式(1)所示[16-17]：

(1)

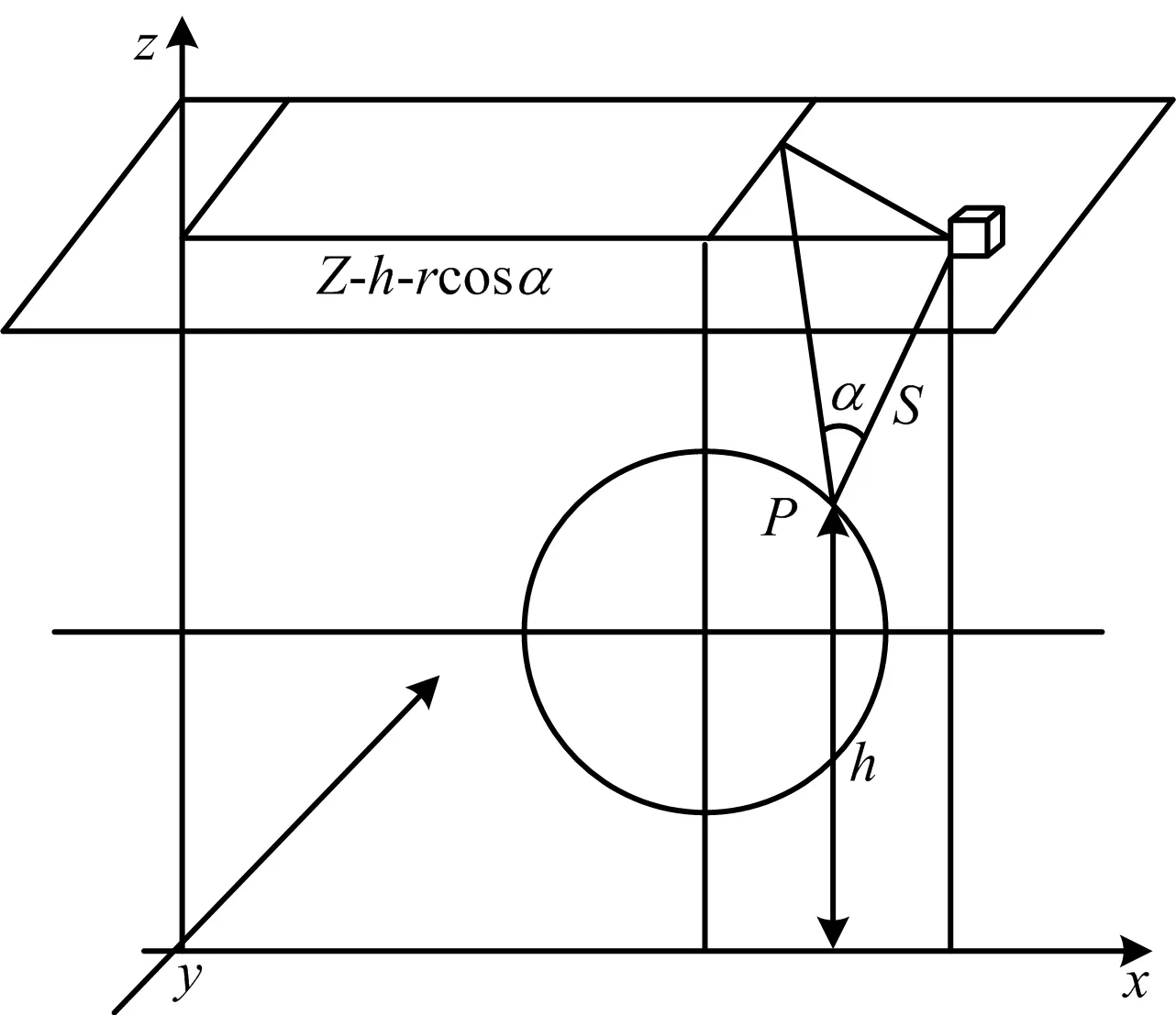
图1 dV对储罐罐壁P点的辐射Fig.1 Radiation of dV to P point on wall of storage tank

火焰对P点的辐射热流量如式(2)～(4)所示：

(2)

(3)

s2=(x-a)2+(y-sinθ)2+(z-h3-rcosθ)2

(4)

式中：Q为辐射热，W；k为导热系数，W/(m·K)；V为积分区域，是P点的切平面以外的火焰区；q为辐射热的流量，W/m2；σ为蒂夫-玻尔兹曼常数，5.67×10-8W/(m2·K4)；Tf为火焰内稳定区域温度，K；α为火焰倾斜角度，(°)；θ为纬度角，是储罐壁上P点和火焰微元连线与P点法线的夹角，(°)；s为火焰内任意微元距储罐壁上P点距离，m；h为储罐壁上P点高度，m；x，y，z分别为火焰微元在坐标轴上对应距离，m；r为火焰半径，m。

1.2 球罐传热模型

1)球罐外部传热模型

假设外部边界条件均匀分布，边界条件主要为热辐射，其次为热对流，数学表达式如式(5)～(7)所示：

(5)

qt=εwσ(tf4(τ)-tw4)

(6)

qc=hfc(tf(c)-tw4)

(7)

式中：λ为罐壁导热系数，W/(m·K)；δ为壁厚，m；tw为球罐外壁温度，随时间、位置的改变而变化，K；qt为火灾环境与球罐罐壁间辐射热流量，W/m2；qc为火灾环境与球罐罐壁间对流热流量，W/m2；εw为球罐罐壁黑度，介于0～1之间；σ为黑体辐射系数，5.67×10-8W/(m2·K4)；tf为火焰温度，K；hfc为对流换热系数，W/(m2·K)。

2)球罐罐壁导热

总而言之，在当前新媒体环境下，积极推进高校学生心理健康教育有着很大的必要性，但要想不断推进高校大学生心理健康教育工作的开展，还需要高校紧密结合学生的发展特性，充分发挥新媒体技术的优势，以此不断推进高校心理健康教育的发展。

球罐罐壁导热方式为热传导，模型为球形储罐，导热微分方程如式(8)所示：

(8)

式中：T为罐壁温度，K；λ为罐壁导热系数，W/(m·K)；ρ为罐壁密度，kg/m3；c为罐壁比热，J/(kg·K)。

2 球罐热-结构耦合分析

2.1 球罐设计参数

本文选取2 000 m3球罐为研究对象，罐壁材料为Q345R，上下柱材料为Q235A，主要构件参数见表1。

表1 球罐主要结构及参数Table 1 Main structure and parameters of spherical tank m

2.2 球罐模型建立

采用Workbench模型中的Static Structural模块，运用其自带软件Designmodel进行建模。由于整个球罐模型较大，且球罐为周期对称图形，为节省计算时间，提升工作效率，对其进行对称处理。采取自动划分与多区划分相结合的方法对模型进行网格划分，并选取球罐1/10进行分析。网格单元总数15 873,节点总数48 356,网格质量数值0.929，划分结果如图2所示。

假设储罐被火焰包围，处于均匀热辐射状态，可认为火焰与罐壁相切，即α= 90°，h=0，将球罐尺寸参数带入池火灾公式(1)～(4)，得辐射热通量约50 kW。

2.3 罐壁温度场分析

本文以充装率85%的球罐为例，施加温度荷载后，得到球罐温度场云图如图3所示。由图3可知，球罐温度最高部位出现在气相区，最高温度可达619.66 ℃，气相区温度远远高于液相区温度。在气液交界处出现明显分层现象，此处存在较大温度梯度。

为更加直观显示罐壁温度分布，将球罐切开，观察切口温度分布并放大，如图4所示。由图4可知，球罐罐壁温度呈梯度变化，气相区与液相区温度较稳定，气液过渡区温度梯度较大。

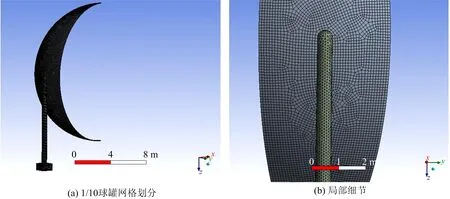
图2 网格划分及局部细节Fig.2 Spherical tank meshing and local details

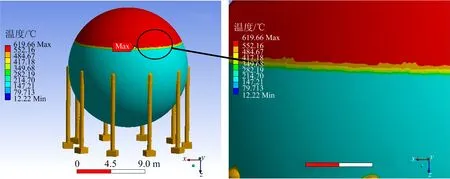
图3 球罐温度场云图Fig.3 Cloud diagram of temperature field on spherical tank

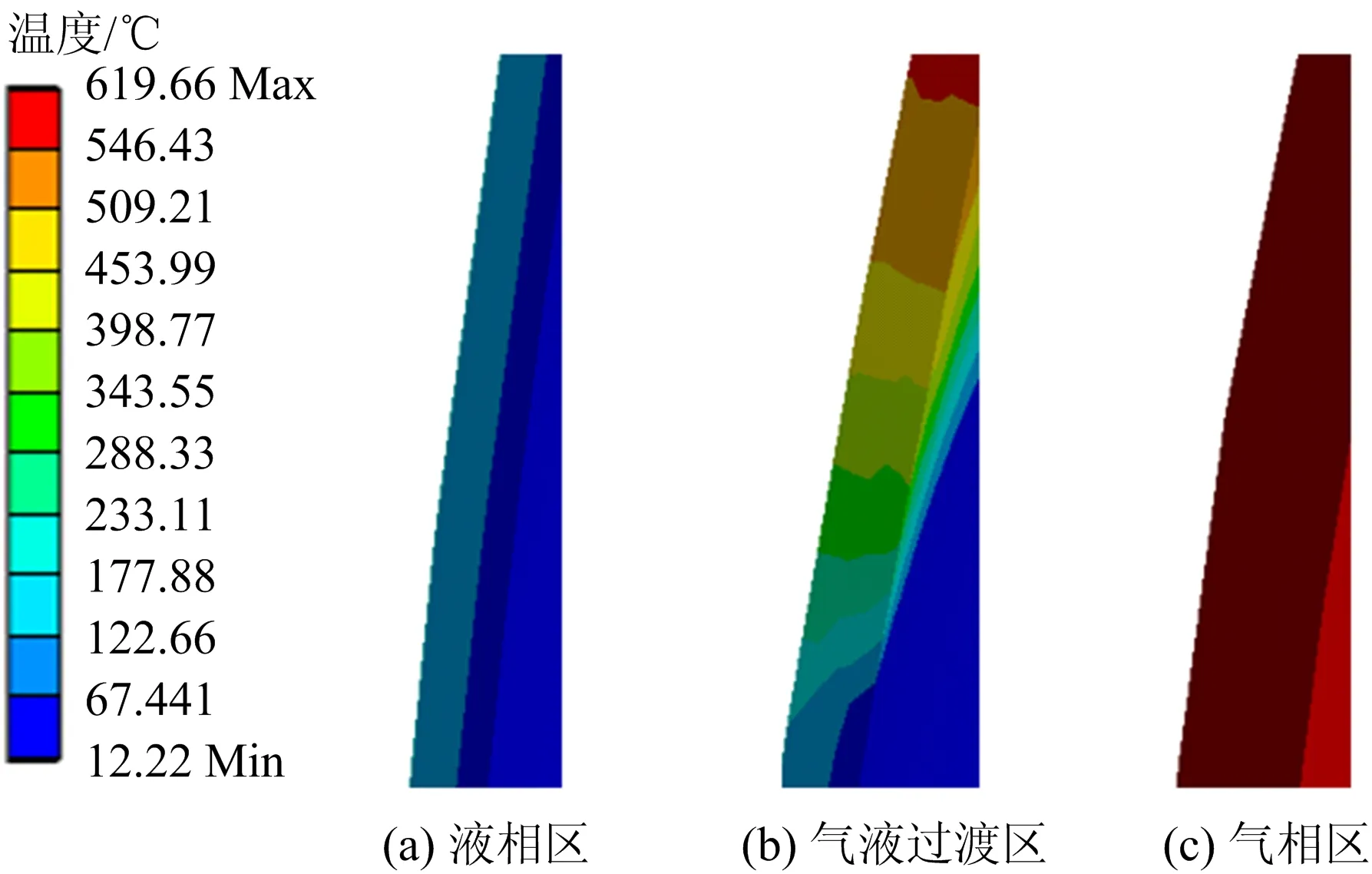
图4 不同区域罐壁温度分布Fig.4 Temperature distribution of different areas on tank

2.4 介质温度场分析

液相区温度分布如图5所示，每条曲线代表不同液位高度(物料半径从1～6 m，间隔1 m的6个水平高度)LPG的径向温度分布。由图5可知，液相区温度随LPG液位升高而增大，靠近油罐壁时温度迅速升高，最终温度几乎相同，液相区主体温度无明显变化。

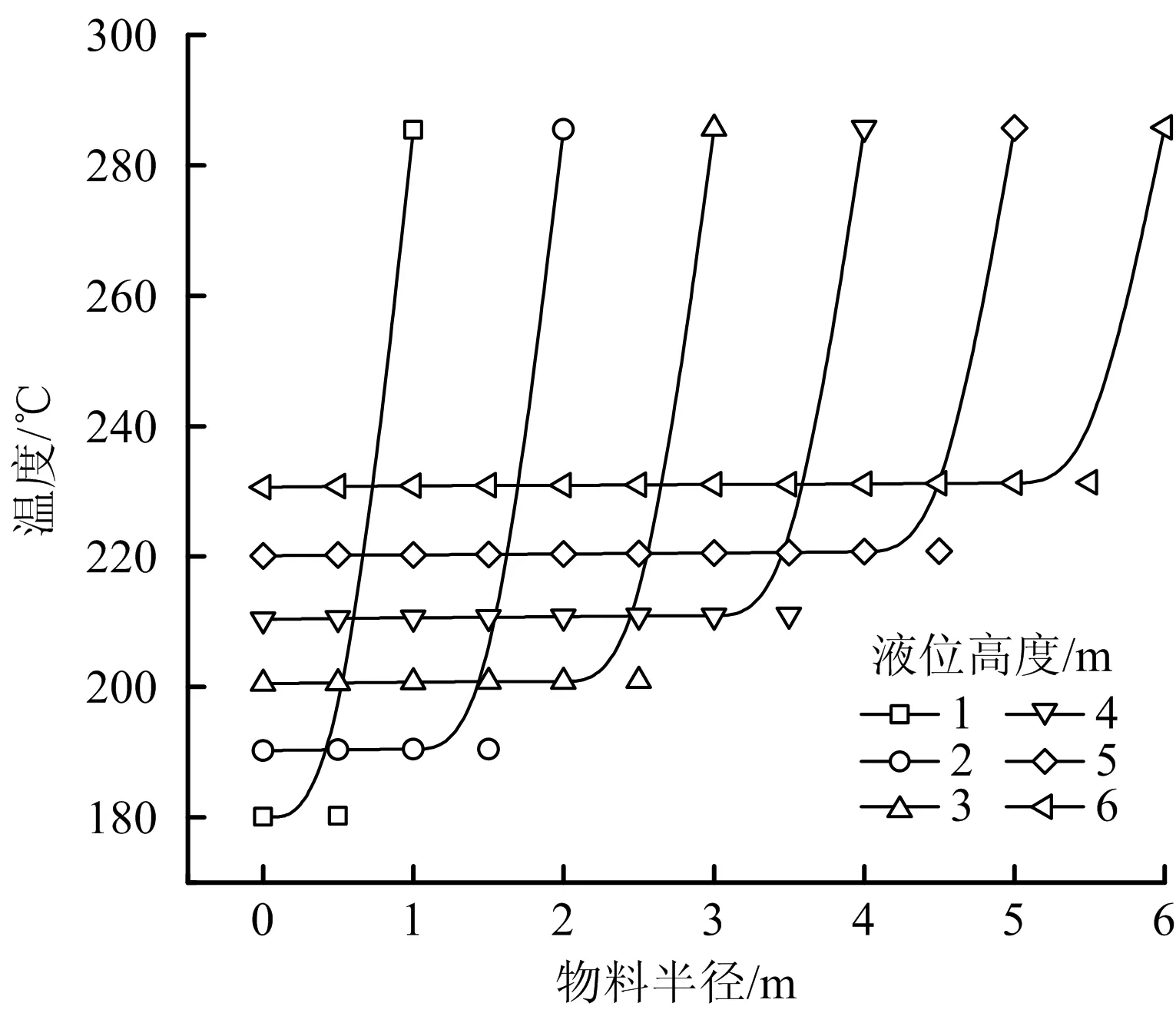
图5 液相区温度分布Fig.5 Temperature distribution in liquid phase zone

2.5 应力分析

球罐在火场中受到的载荷包括：自身重力、液体静压力、热应力和液体饱和蒸气压。其中重力和液体静压力为固定载荷；热应力可利用ANSYS 间接分析法求解；饱和蒸汽压力为随温度变化的载荷，当到达安全阀设计压力时，阀门开启，压力不再上升，忽略阀门开启时的压力波动，取设计压力2.16 MPa进行加载，最终得出球罐整体应力分布及球罐形变云图，如图6～7所示。

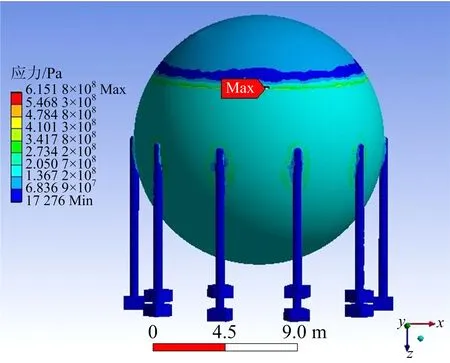
图6 球罐整体应力分布Fig.6 Overall stress distribution of spherical tank

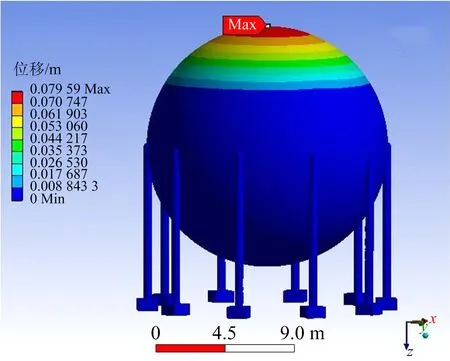
图7 球罐形变云图Fig.7 Cloud diagram of spherical tank deformation

由图6～7可知，球罐最大应力值出现在气液交界处，约615.18 MPa。这是由于气液交界面处载荷不连续，且存在较大温度梯度，产生较大热应力；另外此处温度值较高，所以此处为最危险部位，这与米静[15]的研究结果一致。在支柱与球罐连接处，由于结构发生变化，存在较大应力区域，应力值达290.89 MPa；位移最大部分出现在罐顶区域，最大位移值约0.079 m。

3 球罐失效判定

3.1 球罐失效准则建立

在真实火场环境下，当外部载荷到达一定数值，球罐到达应力极限就会发生破裂失效，不会随载荷增加无限增大。利用有限元模拟找到球罐失效应力值和对应载荷意义重大。

压力容器失去正常功能即认定失效[18]。针对不同行业和受众，失效准则不同：对于工业厂商，应力值大于等于许用应力时，设备已经处于非正常工作状态，即认定失效；但在实际火灾环境中，球罐大都处于故障状态，应力值甚至达到屈服强度，形态上发生明显变化；对于消防救援人员，只要储罐没有发生破裂，仍然可以继续进行灭火行动。因此，工业上失效标准不可以直接用来指导液化气储罐灭火救援行动。

结合消防救援实际情况，定义球罐应力值达到抗拉强度时储罐失效，此时储罐发生破裂，极易发生爆炸，危险性极高。为保障消防救援人员人身安全，给指战员预留充足反应时间，需在储罐失效前设置预警值：当储罐应力值达到许用应力时，发出第1次预警，此时仅储罐故障，危险性较小；应力值达到屈服应力时，发出第2次预警，此时储罐已经发生不可恢复性永久位移；如果应力值得不到控制，储罐最终将破裂失效，此时危险性极高。

根据《钢制压力容器—分析设计标准》(JB 4732—1995)(2005年确认)，对罐壁材料Q345R在不同温度下许用应力、屈服强度和抗拉强度进行数据拟合，拟合函数公式见表2。拟合指数R2均接近1，说明拟合效果较好。得到拟合函数后，通过插值法计算不同温度下Q345R许用应力、屈服强度和抗拉强度，确定储罐状态。

表2 拟合函数表达式Table 2 Expressions of fitting function

3.2 球罐失效及预警判定

为更好地确定储罐预警应力值和失效应力值，需要找到球罐失效边界条件，在实际火场中，若测得球罐温度值与应力值即可确认此时球罐状态。火场中利用远距红外测温仪测量温度值，利用长距离应力测试仪测量应力值。

结合上文中极限辐射热通量及许用应力、屈服强度、抗拉强度数值，采用插分法，通过带入不同辐射热通量值，多次模拟计算后求得球罐失效及预警时温度和应力值，结果如图8～10所示。

图8 第1次预警应力场云图及判定Fig.8 The stress nephogram and judgement of the first warning

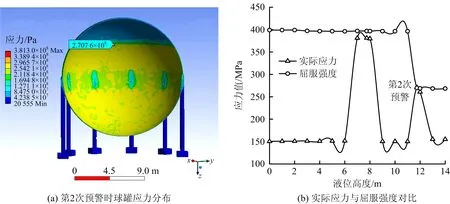
图9 第2次预警的应力场云图及判定Fig.9 The stress nephogram and judgement of the twice warning

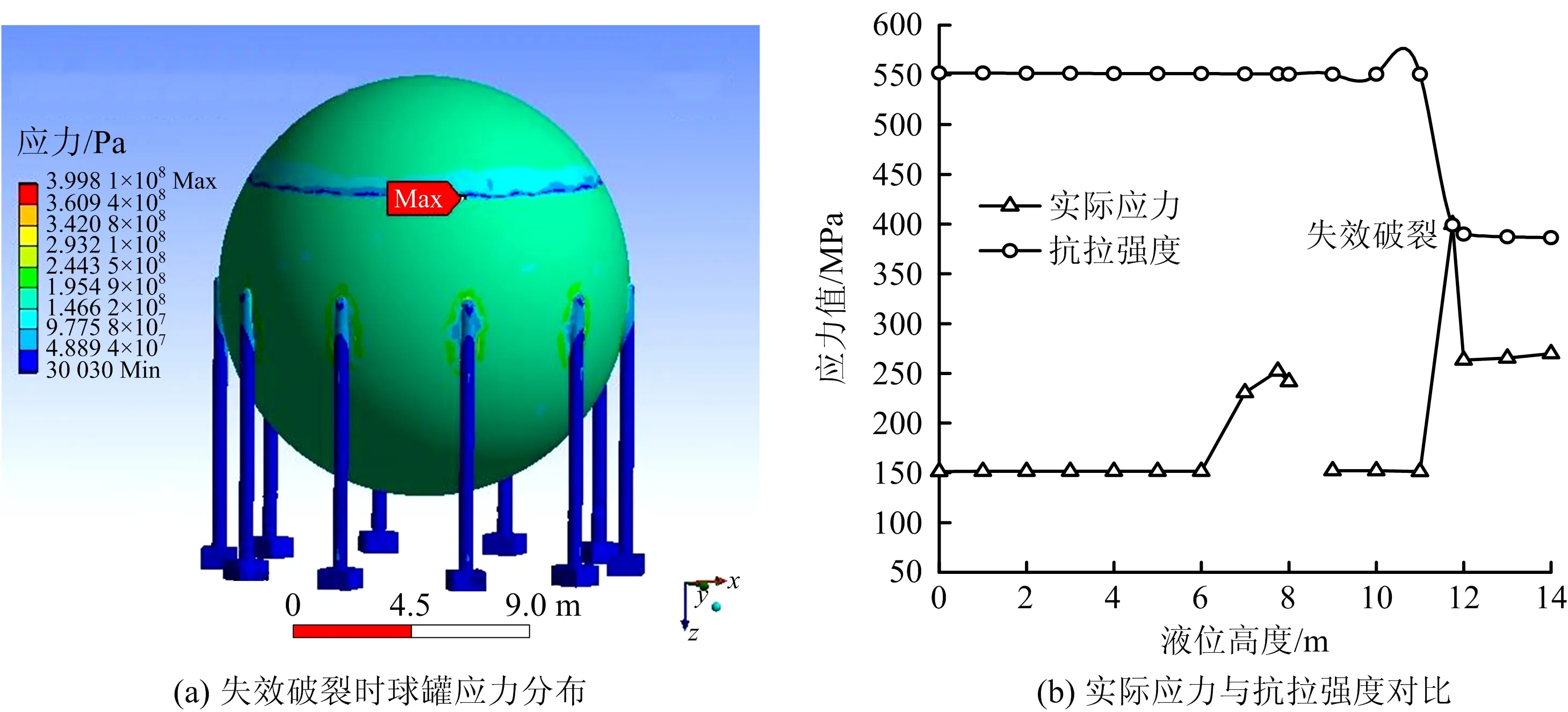
图10 失效破裂时应力场云图及判定Fig.10 The stress nephogram and judgement when failure burst occur

由图8～10可知，当降低热辐射通量，温度下降热应力变小，此时机械应力大于热应力，球罐最大应力值部位为支柱与罐壁连接处。虽然此时支柱与罐壁连接处应力值最大，但由于气液交界面处温度更高，所以最先达到预警值和失效值。

第1次预警时，应力值196.46 MPa，热辐射通量12.92 kW，气液交界面温度值123.41 ℃；第2次预警时，应力值270.76 MPa，热辐射通量27.79 kW，气液交界面温度值358.57 ℃；球罐破裂失效时，发出第3次预警，应力值399.81 MPa，热辐射通量35.02 kW，气液交界面处温度值413.33 ℃。

消防指战员在指挥火灾现场时，首先测出球罐表面最高温度和实时应力，然后根据温度值计算球罐预警及失效破裂时理论应力，若实际应力大于理论应力值则发出预警信号，进而确定下一步消防措施，保护消防救援人员安全。