混杂纤维增强应变硬化水泥基复合材料的弯曲性能预测
2021-03-11夏超凡李志华
张 聪,夏超凡,袁 振,李志华
(1.江南大学 环境与土木工程学院,江苏 无锡 214000; 2.武汉理工大学 硅酸盐建筑材料国家重点实验室,湖北 武汉 430000; 3.中国建筑材料科学研究学院 绿色建筑材料国家重点实验室,北京 100024)
应变硬化水泥基复合材料(SHCC)的极限拉伸应变大、延性好,近年来受到了土木工程领域的广泛关注[1-6].但是由于成本原因,SHCC的推广应用依然存在瓶颈.纤维混杂化是提高SHCC性价比的重要手段之一[7-20].近年来,国内外学者对钢纤维(SF)/聚乙烯醇(PVA)纤维混杂应变硬化水泥基复合材料(SF-PVA/SHCC)的基本力学性能开展了广泛的试验研究[8-20].相比于直接拉伸试验,弯曲试验更容易开展且其数据离散较小.而且从结构材料的工程应用角度来看,深入了解SF-PVA/SHCC的弯曲性能是其在建筑结构构件中应用的前提.近年来,国内外学者对PVA纤维混杂应变硬化水泥基复合材料(PVA/SHCC)以及SF-PVA/SHCC的弯曲性能开展了一定的研究,但是目前依然欠缺能够预测SF-PVA/SHCC弯曲性能的理论计算方法.
1 试验
1.1 基体材料
基体选用水泥砂浆,材料包括无锡天山水泥集团有限公司生产的P·O 42.5水泥、河南四通化建有限公司提供的Ⅰ级粉煤灰和精细石英砂(粒径100~210μm,平均粒径150μm),按照m(水泥)∶m(粉煤灰)∶m(石英砂)=1.0∶4.0∶1.8的比例混合,水胶比mW/mB=0.34.瑞士进口的Sika牌聚羧酸高性能减水剂,减水率(质量分数)28.3%,用于调节新拌浆体的工作性,掺量为胶凝材料质量的0.5%.
1.2 纤维材料
钢纤维(SF)由上海真强纤维有限公司生产,有端部弯钩,长度为13mm,直径为0.2mm,长径比为65,抗拉强度为2000MPa,弹性模量为200~210GPa,密度为7.8g/cm3;PVA纤维由日本可乐丽公司生产,长度为12mm,直径为39μm,抗拉强度为 1100MPa,弹性模量为 42.8GPa,密度为1.3g/cm3.试验中各纤维掺量(均以SHCC的体积分数计)如表1所示.
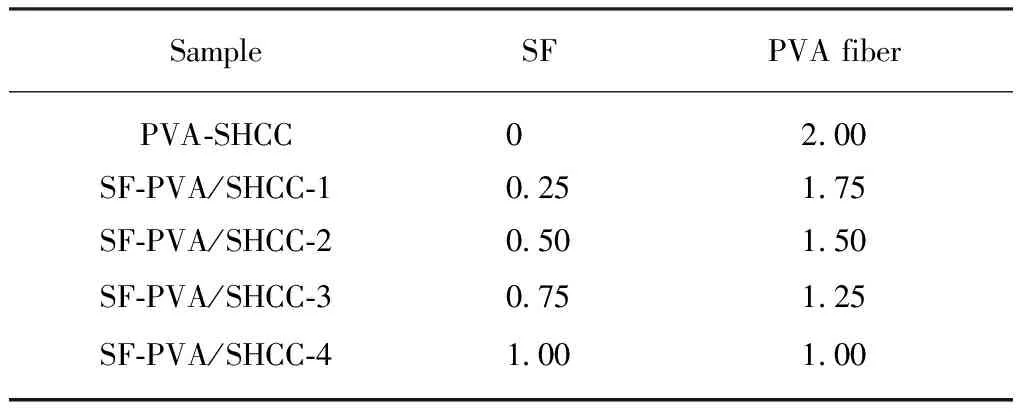
表1 应变硬化水泥基复合材料中纤维掺量
1.3 试件制作
采用无锡建材试验仪器厂的JJ-5型行星式水泥胶砂搅拌机,先将水泥、粉煤灰、石英砂干拌2min;随后加入水和高效减水剂,搅拌2min;最后均匀加入纤维,搅拌5min,获得新拌水泥基材料.搅拌过程中发现,新拌材料工作性良好,纤维分散比较均匀,未发现明显的纤维缠绕与结团现象.采用100mm×400mm×15mm试件测试材料的抗弯性能,每组配合比成型试件3个.参照JC/T 2461—2018《高延性纤维增强水泥基复合材料力学性能试验方法》,新拌材料装模后放入标准养护箱中养护24h后拆模,在(20±2)℃、相对湿度95%的条件下继续养护至28d,将试件取出进行弯曲性能试验.
1.4 弯曲性能试验
采用济南兰博时代测试技术有限公司的WAW-100D型万能试验机,按照图1所示加载装置进行加载.试件跨距为300mm,通过荷载传感器(量程10kN)和位移计(LVDT)测试试件的弯曲荷载及跨中挠度.加载方式为位移控制,加载速率为0.5mm/min.
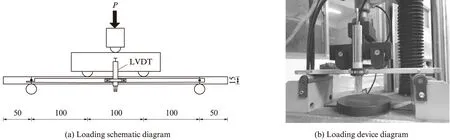
图1 弯曲性能试验加载装置Fig.1 Loading instrument for flexural property test(size:mm)
2 结果与讨论
2.1 弯曲荷载-挠度曲线
图2为各组试件的弯曲荷载-挠度曲线.图3为各组试件的抗弯强度与极限弯曲挠度的平均数据统计.由图2、3可以看出:(1)钢纤维劣化了SHCC的弯曲变形能力,说明PVA纤维对SHCC的弯曲挠度硬化行为起控制作用;随着钢纤维掺量的提高,SHCC的弯曲变形能力将进一步劣化,当钢纤维掺量由0%增加到1.00%时,SHCC的极限弯曲挠度降低了63.7%.这是因为相同掺量条件下,钢纤维的根数和PVA纤维的根数差异太大.因此,实际上纤维的有效桥联应力是不足的[4],导致SHCC的硬化过程和多缝开裂过程并不稳定,从而无法使SHCC表现出明显的高延性.(2)钢纤维提高了SHCC的弯曲承载能力,其抗弯强度随着钢纤维掺量的提高而增大,随着钢纤维掺量由0%增加到1.00%,SHCC的抗弯强度提高了57.3%.这是由于本文所采用的超细钢纤维属刚性纤维且带有端部弯钩,而乱向分布的微细钢纤维可以很好地阻碍混凝土内部微裂缝的扩展以及宏观裂缝的发生和发展,对主要由主拉应力控制的抗弯强度有明显的改善作用.而PVA纤维属柔性纤维,相比于微细钢纤维,PVA纤维对SHCC的抗弯强度影响较弱.
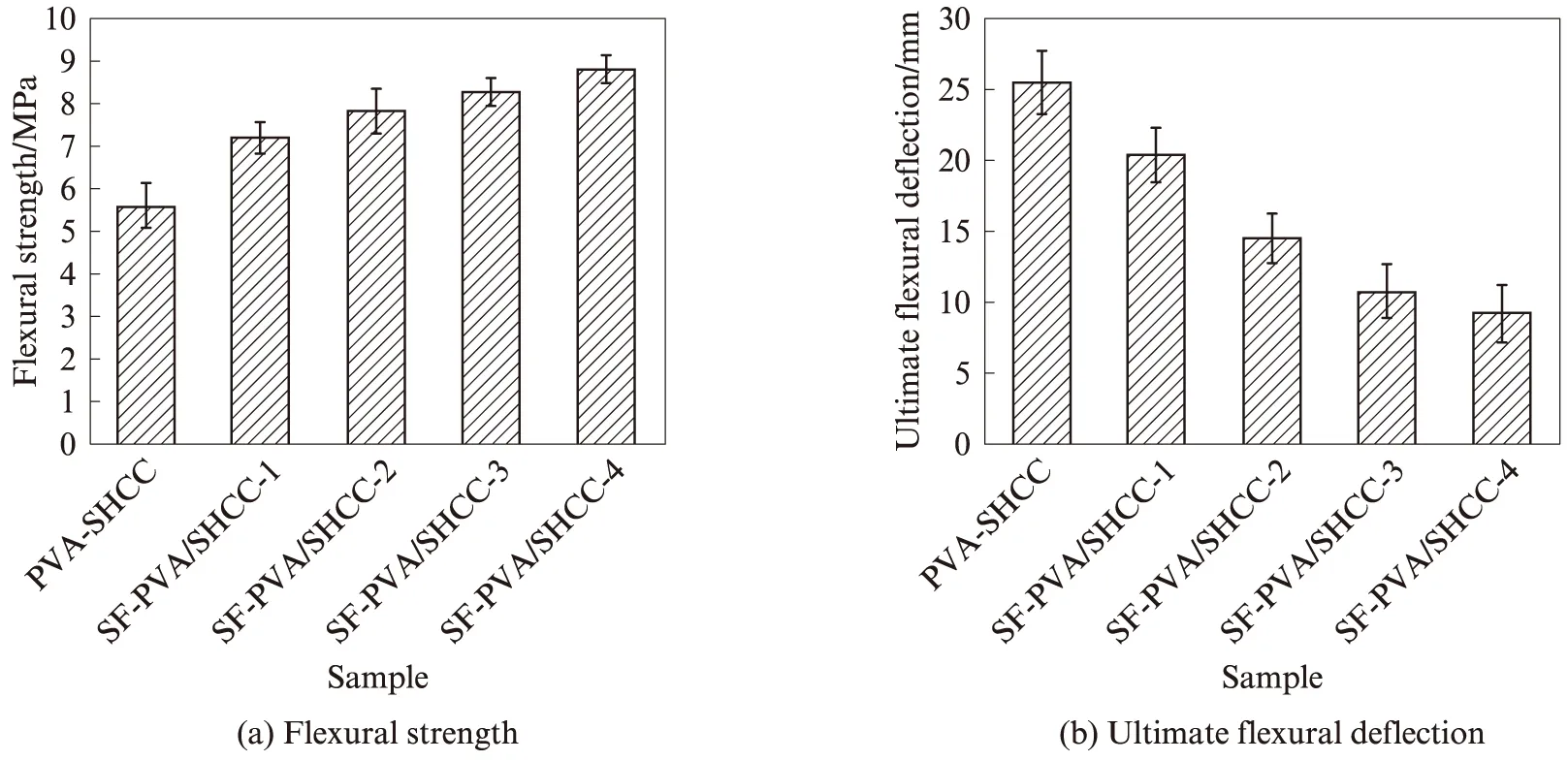
图3 各组试件的平均抗弯强度和极限弯曲挠度Fig.3 Average flexural strength and ultimate flexural deflection of each group sample
2.2 弯曲裂缝形态
图4为各组试件跨中区域的弯曲裂缝形态.由图4可以看出:PVA-SHCC在弯曲荷载作用下表现出了明显的多缝开裂特征,裂缝宽度和裂缝间距均较小;随着钢纤维掺量的提高,试件的弯曲裂缝宽度和裂缝间距逐渐变大,裂缝数量逐渐减少,多缝开裂现象逐渐变得不明显,且出现裂缝局部化的现象.上述发现与各组试件荷载-挠度曲线所表现出来的规律一致:随着钢纤维掺量的提高,荷载-挠度曲线变得更加平滑(多缝开裂行为减弱),极限挠度值逐渐减小(裂缝减少且出现局部化现象).
2.3 弯曲性能预测
2.3.1抗弯强度计算
Maalej等[21]研究发现,SHCC的抗弯强度(极限弯曲应力,σbu)与其抗拉强度(极限拉伸应力,σtu)的比值在1~4之间.在此基础上,本文通过引入纤维增强因子(RIv)[22],用于考虑混杂纤维体积和纤维几何特征的影响,将PVA-SHCC以及SF-PVA/SHCC的σbu与σtu的关系表达为式(1).
(1)
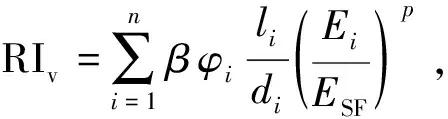
每当母亲用一些类似“牙膏没有从最尾端挤出”“冰箱门没关紧”“看电视超过半个小时”等等小事向我兴师问罪,并且总是将矛头转向我的成绩上面去时,我便知道,夜里,父亲又会来到我的房间。
根据Li等[24]的研究,σtu=gσ0.其中:σ0为纤维桥联应力,按式(2)计算;g为纤维效应系数,按式(3)计算.
(2)
(3)
式中:τPVA、τSF分别为PVA、SF纤维与基体的界面粘结强度,其取值可参考文献[25];φPVA、lPVA、dPVA分别为PVA掺量、长度和直径;φSF、lSF、dSF分别为SF的掺量、长度和直径;Fbe端部弯钩钢纤维的形状特征系数[23],取值范围1.2~2,本文取为1.8;f为界面参数,取值范围0~1,本文根据Ahmed等[20]的建议,取为0.55.
2.3.2极限弯曲挠度计算

(4)
(5)
根据Lin等[28]的研究,εtu可按式(6)计算.
(6)
式中:δcu为裂缝极限开口位移;xd为裂缝极限间距.为简化计算,假设极限状态时裂缝间距相等.

图4 各组试件跨中区域的弯曲裂缝形态Fig.4 Flexural cracking pattern of each group sample in mid-span area
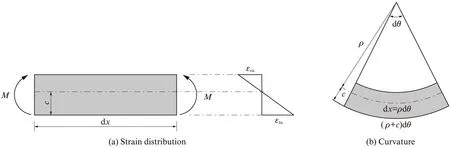
图5 板隔离体的应变分布和曲率Fig.5 Strain distribution and curvature of slab free body
Kanda等[28]以及Li等[29]研究发现,PVA纤维会出现滑移-硬化行为,而刚性纤维如钢纤维会出现滑移-软化行为.Lin等[27]研究发现,如果忽略PVA纤维的滑移-硬化行为,会使δtu明显偏低.对于有滑移-软化现象的钢纤维,δtu取值参考Li等[30]的研究.根据Lin等[27]的建议,考虑PVA纤维滑移-硬化行为,δtu可按式(7)计算.
(7)
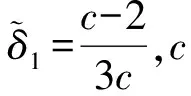
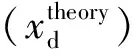
(8)
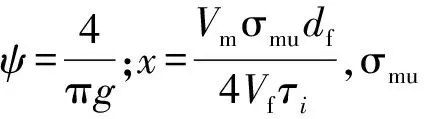
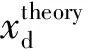
(9)

表2为各组试件抗弯强度σbu和极限弯曲挠度(D)的理论计算结果与试验结果的对比,其中σbu-theory/σbu-test均值为0.98,标准差为0.061,变异系数为0.062,Dtheory/Dtest均值为1.06,标准差为0.037,变异系数为0.035.
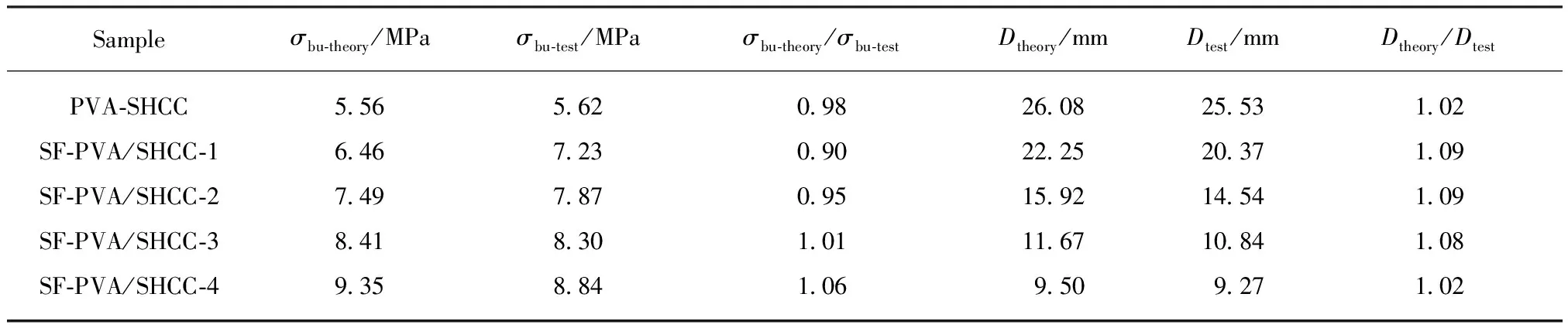
表2 各组试件的平均抗弯强度和极限弯曲挠度的理论值与试验值对比
从表2可以看出,计算模型可以较好地预测SF-PVA/SHCC的弯曲性能.其中,极限弯曲挠度的理论计算结果均高于试验结果,是因为理论计算中假定裂缝是均匀等间距分布的,是一种理想状态,而实际试验中SHCC的裂缝分布不均匀,裂缝开展是不充分的,因此实际情况下SHCC极限挠度的试验值低于理论计算值.
3 结论
(1)钢纤维劣化了SHCC的弯曲变形能力和多缝开裂能力;随着钢纤维掺量由0%增加到1.00%,SHCC的极限弯曲挠度降低了63.7%;随着钢纤维掺量的提高,SHCC的弯曲多缝开裂能力进一步劣化;钢纤维对提高SHCC的弯曲承载能力有利,材料的抗弯强度随钢纤维掺量的提高而增大,随着钢纤维掺量由0%增加到1.00%,SHCC的抗弯强度提高了57.3%.
(2)本文提出的弯曲性能计算方法可以较好地预测SF-PVA/SHCC的抗弯强度和极限弯曲挠度.
