基于一维耦合腔光子晶体的声光可调谐平顶滤波器的研究

2021-03-11张若羽李培丽

物理学报 2021年5期

张若羽李培丽

(南京邮电大学电子与光学工程学院, 南京 210023)

本文利用一维耦合腔光子晶体, 提出了一种声光可调谐平顶滤波器.该滤波器利用声光效应, 通过改变超声波频率使一维耦合腔光子晶体透射谱的平顶滤波器的中心波长产生漂移, 从而实现可调谐的滤波功能.基于传输矩阵法和声光效应理论, 建立了这种平顶滤波器的理论模型; 利用COMSOL 软件, 对平顶滤波器的矩形度、通带带宽、插入损耗、可调谐特性、加工精度进行仿真研究.研究结果表明, 通过施加频率为6—11 MHz的超声波, 可实现通带带宽为5—6 nm 及中心波长在1514—1562 nm 范围内可调谐的平顶滤波器; 在可调谐范围内通带带宽内插入损耗不超过2.23 dB, 最低仅为0.78 dB, 矩形度最低可达1.4; 加工误差在 ± 10 nm 内平顶滤波器的中心波长、矩形度、插入损耗、通带带宽出现的偏差很小.该平顶滤波器具有易于设计和集成、通带平坦、可调谐范围宽、通带带宽稳定、插入损耗低、品质因素高的特点, 在光开关、可调谐光纤激光器、光纤传感等光通信领域有重要应用.

1 引言

随着光通信的普及和发展, 光滤波器作为光纤通信及光网络中最基础的元器件之一, 需求量巨大且应用范围广泛, 其技术水平和产量大小会对光网络的发展产生直接影响[1].可调谐滤波器具有提高光通道的灵活选择性和降低光器件的工作成本的优点.声光可调谐滤波器是一种基于各向异性晶体在声光作用下的反常布拉格衍射效应制成的可调谐滤波器[2].近年声光可调谐滤波器的制作工艺越来越成熟, 具有较宽的调谐带宽, 可以进行多个波长选择[3].声光可调谐滤波器在成像光谱技术、光栅分光技术、半导体激光器可调谐滤光技术等方面取得重大突破[4].光子晶体声光可调谐滤波器[5]结构简单、易于集成、调谐可控, 能够实现光学信息的高效处理, 在光纤通信领域发挥重要作用, 尤其是波分复用、频谱分析等方向.

按照通带滤波特性分类, 一维光子晶体滤波器可分为平坦型滤波器、波纹型滤波器、线性相移型滤波器[6].其中, 一维光子晶体平坦型滤波器的矩形度达到一定程度则可称为一维光子晶体平顶滤波器[7].由于目前对一维光子晶体可调谐平顶滤波器研究较少, 本文对利用声光效应的一维光子晶体可调谐平顶滤波器进行了研究.

1999 年, 加州理工大学的Yariv 提出在光子晶体中周期或非周期性地引入微腔缺陷可以形成耦合腔波导, 并运用了紧束缚近似方法对微腔结构的频带进行描述[8].2000 年, Bayindir 等在实验上首次验证耦合腔光子晶体, 并发展了散射方法、矩阵方法等描述耦合腔结构的其他方法[8].基于这种耦合腔结构对一维光子晶体的局域现象进行广泛研究, 发现一维耦合腔光子晶体具有比不存在耦合腔的光子晶体在光子带隙范围内更高的局域光的能力[9].一维耦合腔光子晶体可应用于全光缓存器、全光信号处理器等光器件.

2 结构设计及工作原理

2.1 结构设计

图1 为设计的基于一维耦合腔光子晶体的声光可调谐平顶滤波器结构图及施加的超声波波形图, 图中光波为平行光, 超声波为纵波, 均垂直入射, a 为超声波振幅, 超声波沿 z 轴传播, 透射光波依然垂直于一维光子晶体介质平面.平顶滤波器由一维光子晶体组成, 结构为(AB)NC(xAxB)K(yAyB)K(AB)N.其中材料A 为氟化镁, 不属于声光材料,折射率 nA=1.38 , 厚度 dA=243 nm ; 材料B 为二氧化碲, 属于声光材料, 折射率 nB=2.06 , 厚度dB=162.7 nm ; 缺陷层C 为空气, 折射率 nC=1 ,厚度 dC=350 nm.缺陷层C 保证了平顶滤波器通带带宽透射率较高, 并且使得一维耦合腔光子晶体可调谐平顶滤波器缺陷模右端低透射区的波段更宽.取周期数 N =15 , K =10 , 倍数 x =0.37 ,y =0.54.

为了保证两种材料A, B 在晶体制备过程中能够晶格匹配, 因而对晶格失配度进行计算.晶格失配度的计算公式[10]:

其中, a1和 a2分别表示交替生长的两种材料的晶格常数, a1>a2; d1和 d2分别表示交替生长的两种材料的晶面间距; θ1和 θ2分别表示交替生长的两种材料的晶面旋转角度.

材料A 氟化镁属于四方晶格结构, 晶格常数为 0.462 nm ; 材料B 二氧化碲属于四方晶系结构,晶格常数为 0.479 nm.根据(1)式, 氟化镁与二氧化碲的晶格失配度为3.5% , 晶体可以顺利生长.

2.2 工作原理

氟化镁和二氧化碲这两种材料周期性地交替生长, 在一维光子晶体中引入缺陷形成耦合腔, 此时光子带隙中就出现了缺陷模[11].如果在一维光子晶体中有多个耦合腔, 相邻耦合腔间距较远时,缺陷模间的耦合作用较弱, 在带隙中会形成较窄且尖锐的通带; 当相邻耦合腔间距较近时, 缺陷模间的耦合作用较强, 缺陷模之间发生耦合, 此时形成了一维耦合腔光子晶体结构, 这一结构特点决定缺陷模形成了较宽且平坦的通带, 在通带范围内可以实现有效滤波[12].

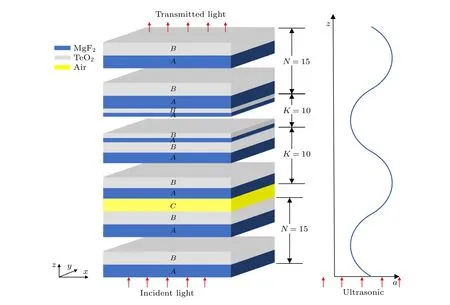
图1 基于一维耦合腔光子晶体中声光效应的可调谐平顶滤波器结构图及超声波波形图Fig.1.Structure diagram and ultrasonic waveform of tunable flat top filter based on acousto-optic effect in one-dimensional coupled-cavity photonic crystals.

当超声波作用于一维耦合腔光子晶体时, 一维耦合腔光子晶体中的声光材料二氧化碲就会产生随时间和空间呈周期性变化的弹性形变, 其折射率和厚度也会随之发生变化[13].一维耦合腔光子晶体折射率和厚度变化后, 缺陷模中心波长发生改变.也就是说, 施加超声场后一维耦合腔光子晶体形成的缺陷模会产生漂移, 因而平顶滤波器透射谱缺陷模的中心波长也会随之发生漂移.

3 理论模型

入射光在一维耦合腔光子晶体中的传输特性可用传输矩阵法来分析, 该平顶滤波器的传输矩阵M[14]为

其中， mj分别代表光在材料 j 中的传输矩阵,j =A,B,C; N , K 为周期数.

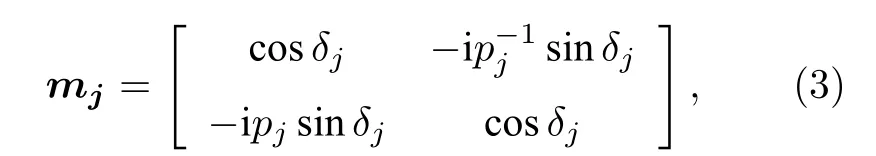
施加超声波后, 声光材料在应力作用下介质会发生一定形变, 折射率和厚度均会发生相应变化.

超声波产生的应变方程为[15]

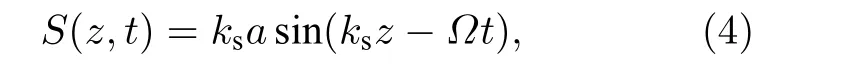
其中, a 表示振幅, Ω 表示声波角频率, t 表示时间,ks表示超声波波矢.

其中, f 表示超声波频率, v 表示超声波波速, 超声波波速与介质材料本身有关.

变化的折射率 ∆ nij和厚度 ∆ dij可分别表示为:

其中, p11为声光系数, ∆ nij和 ∆ dij分别表示光子晶体异质结第 i 层介质对应的材料 j 改变的折射率和厚度, 空气缺陷不算层数.

由于只有材料B 二氧化碲是声光材料, 因此变化的折射率和厚度只考虑B 层的情况, 此时 i 为偶数.

当 2 N +1 ≤i ≤2N +2K 时, 即在一维耦合腔光子晶体的第2 个PC 中,

当2N +2K+1 ≤i ≤2N +4K 时, 即在一维耦合腔光子晶体的第3 个PC 中,

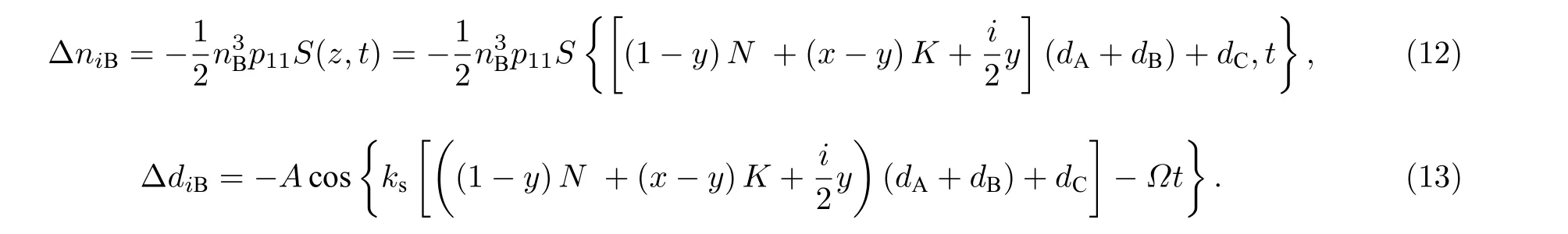
当2N+4K +1 ≤i ≤4N +4K 时, 即在一维耦合腔光子晶体的第4 个PC 中,

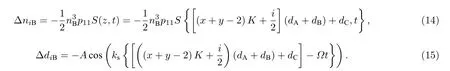
产生声光效应后引起折射率变化和厚度变化,此时的折射率 n 和厚度 d 可表示为:

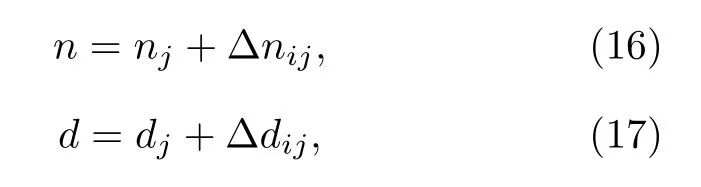
其中, nj和 dj分别表示介质材料 j 原本的折射率和厚度.

光的反射系数r 和透射系数t[16]可用下式表示:

（4）高校的项目库形同虚设。虽然财政部门一直提倡和要求高校要完善项目库，等专项资金到的时候，就可以直接从项目库挑选项目进行资金安排，提高执行效率，但是很多高校并未真正建立项目库，往往都是等专项资金下达后，财务部门将专项资金切块给职能部门，职能部门再组织二级学院进行项目申报，然后进行评审立项，分配资金额度，最后财务部门才下达预算，“分蛋糕”过程需要耗费很多时间，预算效率低下。

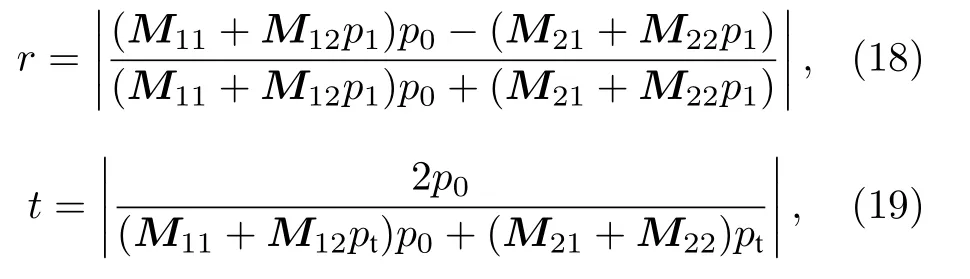
其中, p 的下标0 表示入射空间, 下标1 表示透射空间.

光的反射率 R 和透射率 T 可以用下式表示:

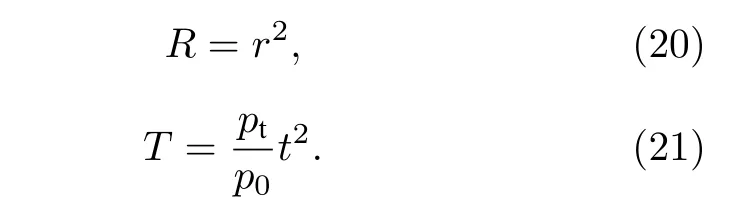
由(4)式、(8)式—(15)式可看出, 改变超声波频率 f 会使得一维耦合腔光子晶体中声光材料的折射率 n 和厚度 d 发生改变, 进而对平顶滤波器中心波长产生影响.因而本文通过改变超声波的频率对平顶滤波器中心波长进行控制.

4 仿真结果及分析

不考虑材料的色散影响和超声波的损耗问题,使用COMSOL Multiphysics 软件对基于一维耦合腔光子晶体中声光效应的可调谐平顶滤波器进行仿真研究.

考虑材料本身的吸收损耗对透射光谱的影响,经过仿真得到如图2 所示一维耦合腔光子晶体的透射谱, 短线和点划线分别代表一维耦合腔光子晶体(AB)15C(0.37A0.37B)10和(0.54A0.54B)10(AB)15的透射谱, 实线代表一维耦合腔光子晶体(AB)15C(0.37A0.37B)10(0.54A0.54B)10(AB)15的透射谱.在一维耦合腔光子晶体(AB)15C(0.37A0.37B)10(0.54A0.54B)10(AB)15中, (AB)15C(0.37A0.37B)10和(0.54A0.54B)10(AB)15两个耦合腔间距较近, 缺陷模发生耦合, 形成了带宽为1559.9—1565.1 nm的平坦通带.在这一通带内透射率高, 通带带宽为5.2 nm , 半高宽为 1 0 nm , 在通带带宽内能够有效滤波.因此能够实现通带较宽、透射率较高的平顶滤波器.

图2 一维耦合腔光子晶体的透射谱Fig.2.Transmission spectrum of one-dimensional coupledcavity photonic crystal.

对一维耦合腔光子晶体施加超声波, 会使声光介质的折射率和厚度发生不同程度的变化, 产生声光效应, 从而平顶滤波器中心波长发生漂移.图3(a)是在不同振幅下平顶滤波器中心波长与超声波频率的关系图.可以看出, 未施加超声波时平顶滤波器中心波长为1562 nm.当超声波频率较小时, 平顶滤波器缺陷模的中心波长随着不同振幅下超声波频率的增加几乎不发生改变; 当超声波频率增加到一定程度, 超声波振幅较大时平顶滤波器中心波长随着超声波频率的增加先向短波方向产生一定漂移.不同振幅的超声波均能通过改变超声波频率实现调谐功能.

图3(b)是在不同超声波振幅下平顶滤波器中心波长与透射率的关系图.可以看出, 当平顶滤波器中心波长从 1 510 nm 增加到 1 514 nm 的过程中,中心波长对应的透射率从37%急剧增加至90%;当继续增大平顶滤波器中心波长至 1 562 nm 的过程中, 不同振幅下中心波长对应的透射率都从90%变为平缓增加至97%.因此漂移的平顶滤波器中心波长范围为1514—1562 nm.

图3 不同超声波振幅下一维耦合腔光子晶体透射谱中心波长随超声波频率的改变 (a)平顶滤波器中心波长与超声波频率的关系图; (b)平顶滤波器中心波长与透射率的关系图Fig.3.Variation of the central wavelength of transmission spectrum of one-dimensional coupled-cavity photonic crystals with different ultrasonic amplitudes: (a) Relationship between the center wavelength of flat top filter and ultrasonic frequency; (b) relationship between the center wavelength of flat top filter and transmissivity.

从图3(a)可以看出, 超声波振幅越大, 平顶滤波器中心波长从 1 562 nm 漂移至 1 514 nm 需要的超声波频率就越小.如振幅为 0.4 nm 的超声波, 仅需频率为 1 1 MHz 的超声波即可使平顶滤波器缺陷模中心波长漂移至 1 514 nm.考虑超声波发生器的成本, 利用最小的超声波频率达到最佳的调谐效果,本文采用振幅为 0.4 nm 、施加频率为6—11 MHz的超声波实现可调谐平顶滤波器.

设置超声波的振幅为 0.4 nm , 改变超声波的频率进行仿真.图4 为平顶滤波器不加超声波、施加频率为 8 MHz 和 1 1 MHz 超声波3 种情况的透射谱.短线、点划线、实线分别代表不加超声波、施加8 MHz 和 1 1 MHz 超声波的透射谱.当不加超声波时, 此时1559.9—1565.1 nm 波长范围的入射光能够通过一维耦合腔光子晶体, 平顶滤波器通带带宽为 5.2 nm , 中心波长为1562 nm, 这一波段可以滤波; 当施加频率为8 MHz 的超声波时, 1537.3—1542.8 nm 波长范围的入射光能够通过一维耦合腔光子晶体, 平顶滤波器通带带宽为5.5 nm, 中心波长为1540 nm, 这一波段可以滤波; 当施加频率为11 MHz 的超声波时, 1511.6—1517.3 nm 波长范围的入射光能够通过一维耦合腔光子晶体, 平顶滤波器通带带宽为5.7 nm, 中心波长为1514 nm,这一波段可以滤波.因此, 可通过施加频率为6—11 MHz 的超声波实现平顶滤波器的调谐功能, 平顶滤波器缺陷模的中心波长调谐范围为1514—1562 nm, 通带带宽为5—6 nm.

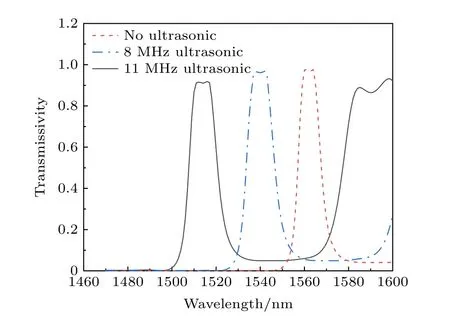
图4 平顶滤波器施加频率8, 11 MHz 的超声波和不加超声波的透射谱Fig.4.Transmission spectra of flat top filter with ultrasonic wave at 8, 11 MHz and without ultrasonic wave.

5 平顶滤波器性能分析

矩形度、通带带宽、插入损耗、加工精度是衡量平顶滤波器的重要指标.本文对基于一维耦合腔光子晶体中声光效应的可调谐滤波器的矩形度、通带带宽、插入损耗、加工精度分别进行研究.

5.1 矩形度

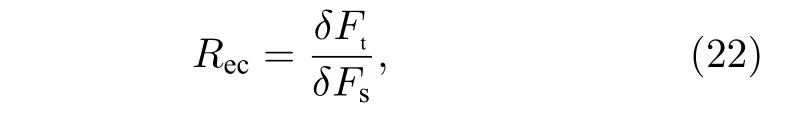
矩形度[17]是指透射谱波形逼近理想方波的程度.矩形度 Rec定义为其中, δ Ft为透射率90%的单个缺陷模宽度, δ Fs为缺陷模单侧透射率大于10%、小于90%的过渡带宽度.矩形度越大则波形越接近理想方波.

平顶滤波器矩形度与中心波长的关系如图5所示, 可以看出在1514—1562 nm 波长范围内矩形度在1.40—1.75 的范围内.随着超声波频率的改变, 矩形度相对稳定.平顶滤波器的矩形度最低达到1.40, 通带相对平坦, 符合平顶滤波器的要求.

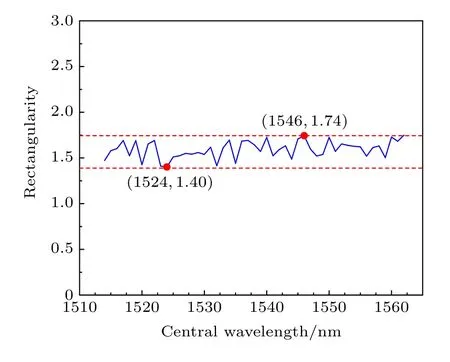
图5 平顶滤波器中心波长与矩形度的关系图Fig.5.Relationship between center wavelength of flat top filter and rectangularity.

5.2 通带带宽

通带带宽[18]是指透射率90%以上的频谱宽度.通带带宽BW 定义为

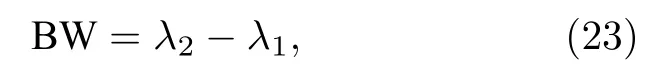
其中, λ1和 λ2分别表示透射谱中透射率为90%的截止波长.

图6 平顶滤波器中心波长与通带带宽的关系Fig.6.Relationship between center wavelength of flat top filter and passband bandwidth.

平顶滤波器通带带宽与中心波长的关系如图6所示, 可以看出随着超声波频率的改变, 1514—1562 nm 波长范围内通带带宽在5—6 nm 之间.该平顶滤波器在调谐过程中通带带宽相对稳定, 滤波带宽在 5.5 nm 左右, 在光通信器件中的光开关、可调谐光纤激光器、信号滤波器等方面有一定应用价值.

5.3 插入损耗

插入损耗[19]是平顶滤波器通带波段内某一波长下输出功率与输入功率之比.插入损耗 Υ 为

其中, Pout是平顶滤波器在通带波段内某一波长下的输出功率, Pin是平顶滤波器在通带带宽内某一波长下的输入功率.

考虑到材料本身损耗的影响, 平顶滤波器插入损耗与中心波长的关系如图7 所示, 其中实线和短线分别表示入射光在这一中心波长下对应的通带带宽内的最大插入损耗和最小插入损耗.随着中心波长的漂移, 施加不同超声波频率时通带带宽内对应的最大插入损耗和最小插入损耗变化不大.最大插入损耗在1.72—2.23 dB 范围内, 最小插入损耗在0.78—1.07 dB 范围内.

图7 平顶滤波器中心波长与插入损耗的关系图Fig.7.Relationship between center wavelength of flat top filter and insert loss.

5.4 加工精度对平顶滤波器的影响

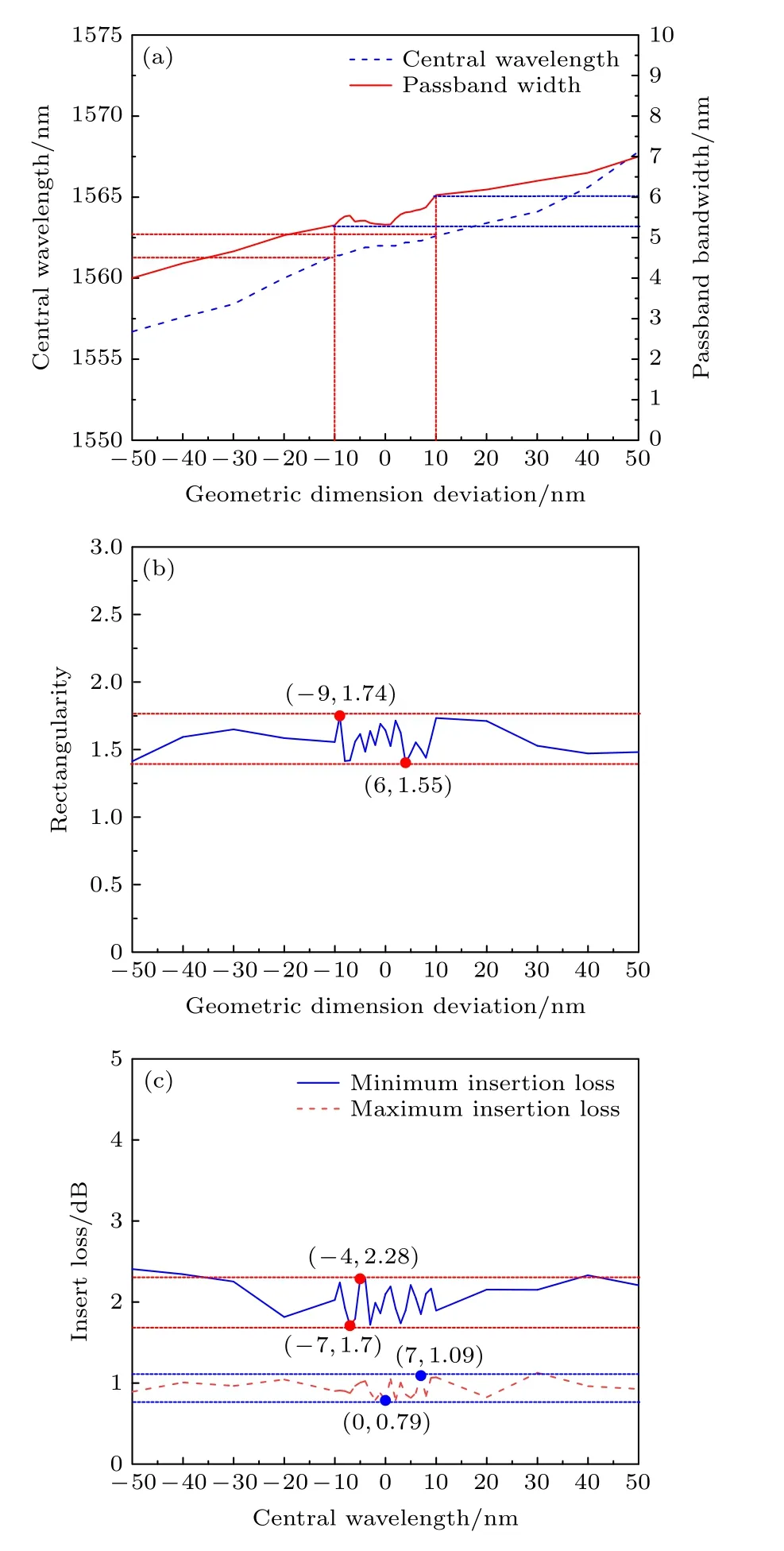
图8 一维光子晶体几何尺寸偏差与相关参数的关系 (a) 一维光子晶体几何尺寸偏差与平顶滤波器中心波长和通带带宽的关系图; (b) 一维光子晶体几何尺寸偏差与平顶滤波器矩形度的关系图; (c) 一维光子晶体几何尺寸偏差与平顶滤波器插入损耗的关系图Fig.8.Relationship between geometric size deviation and related parameters of one-dimensional photonic crystal:(a) Relationship between geometric dimension deviation of one dimensional photonic crystal and central wavelength or passband bandwidth of flat top filter; (b) relationship between the geometric size deviation of one-dimensional photonic crystal and rectangularity of flat top filter; (c) relationship between the geometric size deviation of one-dimensional photonic crystal and the insert loss of flat top filter.

在工程上, 制备一维光子晶体的过程中, 由于工艺水平的限制难免会出现几何偏差, 加工精度会影响到平顶滤波器的中心波长、通带带宽、矩形度、插入损耗等参数.一维光子晶体几何尺寸偏差与相关参数的关系如图8 所示, 正数代表一维光子晶体厚度较标准增加, 负数代表一维光子晶体厚度较标准减少.图8(a)表示一维光子晶体几何尺寸偏差与平顶滤波器中心波长和通带带宽的关系图,实线表示通带带宽, 短线表示中心波长.可以看出随着一维光子晶体几何尺寸偏差从减少–50 nm 到50 nm, 平顶滤波器中心波长向长波方向漂移, 通带带宽呈增加趋势.在 ± 10 nm 的加工精度范围内平顶滤波器中心波长漂移不超过 0.6 nm , 通带带宽在5—6 nm 范围内.图8(b)表示一维光子晶体几何尺寸偏差与平顶滤波器矩形度的关系图, 可以看出在 ± 10 nm 的加工精度范围内平顶滤波器矩形度出现了一定波动, 在这一范围内不低于1.55, 满足平顶滤波器的要求.图8(c)表示一维光子晶体几何尺寸偏差与平顶滤波器插入损耗的关系图, 实线表示通带带宽内最大插入损耗, 虚线表示通带带宽内最小插入损耗.可以看出在 ± 10 nm 的加工精度范围内最大插入损耗不超过 2.28 dB , 相较原平顶滤波器的最大插入损耗仅增加 0.05 dB.

综上所述, ± 10 nm 的加工精度范围内平顶滤波器的中心波长、通带带宽、矩形度、插入损耗出现的偏差很小, 具有容错性.

将近年的平顶滤波器性能与本文的平顶滤波器性能进行比较, 如表1 所示.

从表1 可以看出, 近年来可调谐平顶滤波器主要使用光器件, 通带带宽很窄, 调谐范围集中在1550 nm 通信窗口的研究较少, 尚未有利用声光效应进行调谐的滤波器.虽然一维光子晶体易于集成, 但尚未有利用光子晶体材料制作的声光可调谐平顶滤波器.因而本文设计的声光平顶滤波器更易集成, 通带带宽较宽, 调谐范围集中在通信波段,更具有创新性.

6 结论

本文利用一维耦合腔光子晶体的声光效应, 提出了一种声光可调谐平顶滤波器, 建立了这种声光可调谐平顶滤波器的理论模型, 利用COMSOL 软件进行仿真研究.研究结果表明, 对于不同振幅的超声波, 平顶滤波器中心波长随超声波频率的增加向短波方向漂移, 考虑到平顶滤波器通带带宽内的透射率需超过90%和超声波发生器成本, 选择振幅为 0.4 nm 的超声波, 平顶滤波器中心波长的可调谐范围为 1 514 −1562 nm.平顶滤波器矩形度在1.40—1.75 这一范围内, 插入损耗最低为 0.78 dB ,最高不超过 2.23 dB , 通带带宽在 5.5 nm 左右, 调谐过程中矩形度、通带带宽和插入损耗稳定.在实际工程中, 加工误差在 ± 10 nm 内, 平顶滤波器的中心波长、矩形度、插入损耗、通带带宽出现的偏差很小.本文设计的可调谐平顶滤波器易于集成, 透射谱通带平坦, 具有调谐功能, 可应用于频谱分析、可调谐光纤激光器、信号滤波器等方面.