电解质浓度对胶体粒子表面有效电荷的影响*

赵小安 徐升华† 周宏伟 孙祉伟

1) (中国科学院力学研究所, 微重力重点实验室, 北京 100190)

2) (中国科学院大学工程科学学院, 北京 100049)

胶体粒子的表面有效电荷是决定胶体性质的重要物理量, 但溶液环境(如电解质溶液浓度)是否影响其数值至今尚无统一认识, 近年来的一些研究工作给出了存在争议的不同结果和假设.在直接实验测量方面,由于电解质离子和胶体表面吸附离子的置换, 粒子表面基团的不完全电离和胶体粒子对离子吸附的共同作用, 使得对这类粒子在不同溶液环境下的表面有效电荷的测量和变化机理的认识极为困难.针对该问题, 本文测定了羧基和磺酸基修饰的聚苯乙烯胶体颗粒在不同粒子浓度和HCl 浓度下的电导率, 由于两种粒子与HCl 电离产生的阳离子相同(均为H+), 可根据电导率−数密度法(迁移法)得到胶体颗粒表面有效电荷数.通过实验结果分析, 明确了HCl 浓度以及粒子数密度对胶体粒子表面电荷的影响规律以及表面电荷随HCl 浓度增大的原因.除此之外, 羧基修饰颗粒比磺酸基修饰颗粒的表面电荷随HCl 浓度变化更快; 对于同一HCl 浓度, 磺酸基修饰胶体表面电荷不受粒子数密度影响, 而羧基修饰胶体颗粒却与之相关.基于粒子表面电荷的理论模型, 对这些问题都给出了相应的解释.

1 引 言

胶体粒子之间的相互作用是影响胶体诸多性质和行为的重要因素, 包括胶体的稳定性[1,2]、胶体的无序有序相变[3,4]等.根据DLVO (Derjaguin−Landau−Verwey−Overbeek) 理论, 带电胶体粒子之间存在范德瓦耳斯吸引作用与静电排斥作用[5−7],而排斥作用可表示为Yukawa 势的形式[8,9], 如公式(1)所示, 其中, Ze为粒子表面有效电荷数,ε0和 εr分别是真空介电常数和相对介电常数, a 为粒子半径, r 为两胶体颗粒中心间距.(1)式中的 κ 是徳拜屏蔽常数, 其表达式如(2)式所示, 其中 φ 为粒子的体积分数, v0表示单个粒子体积(即 4 πa3/3 ),Ms为电解质摩尔质量, C0为电解质浓度.因此带电胶体的表面带电特性是决定静电排斥力大小的重要参量之一.

鉴于表面有效电荷数的重要性, 在表面有效电荷相关理论模型、计算与分析以及测量方法等方面都有许多研究工作报道[10−15].然而, 表面有效电荷在测量和应用中仍存在很多问题, 例如不同方法获得的表面有效电荷往往有很大差异, 通过测得的胶体晶体弹性模量反推得到的弹性有效电荷, 要比利用电导率−粒子数密度关系法直接测量得到的迁移有效电荷小40%左右[11].近几年才发现这一差异主要是由于反推弹性有效电荷的理论未考虑孔隙的影响而导致的, 通过对理论的修正, 已经使得反推的弹性有效电荷与测量的结果有了很好的一致性[16].

表面有效电荷的直接测量一般都是在不加电解质的情况下进行, 然而很多实验体系中都加入了电解质, 但表面有效电荷的数值是否随电解质浓度而变化目前仍无定论.随着聚集行为及粒子间作用力等方面研究的不断深入, 近些年来的一些新的实验结果都通过外加离子会影响表面有效电荷的方式来进行解释.Heinen 等[17]针对加入电解质并发生聚集的体系, 测量了体系的聚集时间, 进而根据DLVO 理论, 基于流体动力学作用, 逆推得到胶体表面有效电荷随电解质溶液浓度增大而增大, 并建立了表面有效电荷数和盐浓度的关系式.Gutsche 等[18]通过光镊测量的粒子间相互作用势反推了粒子表面有效电荷, 也认为电解质会对表面有效电荷产生影响.但这些结果都是通过理论公式反推得到的,缺乏直接的实验测量结果的支持.

在实验测量方面, 如果加入电解质将不可避免地存在电解质离子与胶体表面吸附离子的交换, 一般情况下由于难以确定离子的交换量, 从而无法通过电导率−粒子数密度关系法直接测量出表面有效电荷.Hessinger 等[15]通过实验发现加入盐溶液后胶体体系的电导率会出现异常变化, 他们假定表面有效电荷与电解质浓度无关, 从而认为这一现象完全是由于电解质溶液电离的阳离子与胶体粒子和水电离的H+发生置换而导致的.但这一假定是否合理仍值得商榷, 实际上电解质的加入会压缩双电层, 这有可能会减少胶体表面的吸附离子, 从而影响表面有效电荷, 文献[15]中电导率的异常变化也可能是表面有效电荷发生变化而导致的.

因此, 为了解决表面电荷是否与离子浓度有关的争议, 有必要从实验上直接测量不同离子浓度下的表面有效电荷, 以澄清胶体粒子表面有效电荷是否与离子浓度有关, 这对于进一步认识表面有效电荷的相关特性, 以及明确反推表面有效电荷的相关理论是否合理都有重要意义.电导率法是测量水中胶体粒子表面有效电荷的常用方法, 但是如果体系中引入其他电解质, 阳离子与H+发生置换的量和表面有效电荷这两个参数都是待定的, 因而无法从测量电导率得到这两个参量的值, 这也是Davis等[19−21]引入额外假设的原因, 但其假设的合理性难以验证.为了避免阳离子与H+发生置换对测量结果的影响, 本研究选取HCl 溶液作为电解质, 使用磺酸基(强酸, H+可完全电离)与羧基(弱酸,H+不能完全电离)修饰的聚苯乙烯胶体颗粒, 因而确保了该分散液体系中H+为唯一阳离子, 无论是否发生溶液中的阳离子与粒子电离的阳离子的置换, 都可以从实验测得的电导率得到粒子的表面有效电荷, 从而更可靠地来确定表面电荷是否与外加离子浓度有关.

基于电导率与粒子表面有效电荷关系的理论模型, 结合实验结果的分析, 本文较为系统地给出了电解质溶液浓度、粒子数密度以及电荷基团对表面有效电荷的影响规律和机制, 对于澄清表面电荷的影响因素以及在不同参数条件下表面电荷和相互作用的研究和应用都有重要参考价值.

2 材料与实验

2.1 聚苯乙烯胶体制备与参数

为了比较强酸和弱酸修饰胶体粒子的差异, 本文分别使用了羧基修饰和磺酸基修饰的两种聚苯乙烯胶体粒子进行实验.两种微球均购于上海辉质生物有限公司, 其粒径和多分散度如表1 所示.在实验之前, 对测定样品进行过滤和高速离心处理,通过重量法测定固含量, 并利用阴阳离子交换树脂对两种粒子进行30 h 以上去离子处理, 以减少初始杂质离子对实验的影响, 再分别制备颗粒体积分数为0.5% (磺酸基修饰PS)和10% (羧基修饰PS)的聚苯乙烯胶体, 以备后续实验使用.由于样品表面带有较高的电荷, 所以可以长时间保持稳定.另外, 在分析粒子的表面有效电荷时需要用到粒子的电迁移率, 还使用Zeta 电位分析仪(Zeta−Plus, Brookhaven, USA)测量了其迁移率, 其结果列在表1 中.

表1 实验中所使用的粒子参数Table 1.Parameters of the particles.

2.2 实验方法

本文使用电导率−数密度法确定胶体颗粒表面有效电荷.实验装置包括数字电导率测量仪(DDS−12A, 上海鹏顺科学仪器有限公司, 上海)、恒温水浴(Circulator RH25−6A, Labtech International Ltd., United Kingdom)和磁力搅拌器(RCT Basic S25, IKA Word Inc., Germany), 如图1 所示.本文实验全程通过恒温水浴保持实验样品温度为25 °C.首先加入一定量需测定浓度的HCl 电解质溶液至储液瓶中, 待电导数值稳定, 再使用移液器(research plus pipette, eppendorf, Germany)分次向储液瓶中滴入50 µL 配制的待测胶体(该待测体系中的HCl 浓度与初始HCl 浓度一致, 从而可保证在整个实验过程中HCl 浓度稳定).每次添加结束时, 开启磁力搅拌器把储液瓶内样品搅拌均匀, 直到电导率仪的数值不再发生变化后记录读数.针对不同的HCl 初始浓度, 重复上述实验, 可得到一系列不同HCl 浓度及不同胶体粒子数密度所对应的电导率数据, 以用于后续的数据分析和处理.实验过程中, 需控制实验时间尽可能短且电解质溶液浓度较低, 以防止胶体颗粒在电解质溶液中聚集[21]而影响测量的精度, 从而可有效保证实验的准确性.

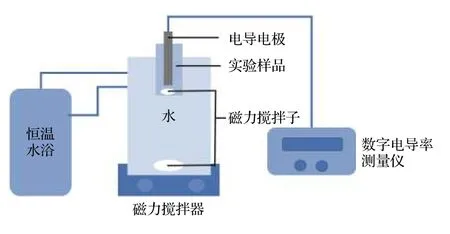
图1 实验装置示意图Fig.1.Schematic diagram of experimental equipment.

3 结果与讨论

3.1 理论模型

为了根据实验测量的电导率计算表面有效电荷, 需要电导率与电荷之间的关系式.Delgado 等[22]最先使用经验公式计算有效电荷数:

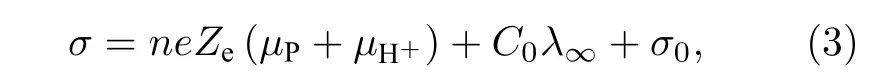
其中, λ∞表示无限稀释情况下的电解质溶液的摩尔电导率; C0为摩尔浓度; σ0为背景电导率(包括水的电离及未知离子); e 为元电荷; µP和 µH+分别表示被测粒子和H+的电迁移率.

事实上, 双电层内外部存在离子交换, 并且电荷总量维持稳定[23,24], 即电解质所电离的阳离子与胶体粒子表面的阳离子发生置换, 因此, 将电解质电导率用 C0λ∞直接相加并不合理, 而将置换后的离子的迁移率进行平均, 可在考虑离子置换的贡献前提下, 得到有电解质存在情况下胶体的电导率[15],如公式(4)所示:

若体系中增加的电解质阳离子以po+表示, 阴离子以ne—表示, 则公式(4)可展开为

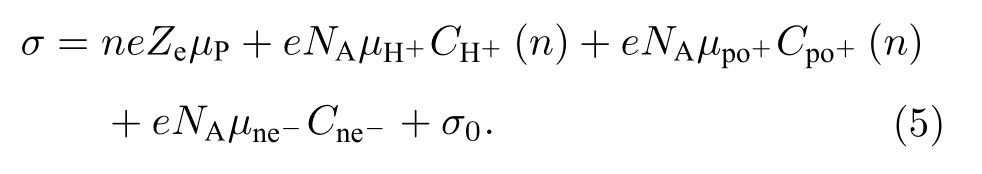
由于电解质阳离子与双电层内部的H+可能发生置换, 因而 Cpo+(n) 并不等于 Cne-, 但考虑到置换后体系仍为电中性, 因而有

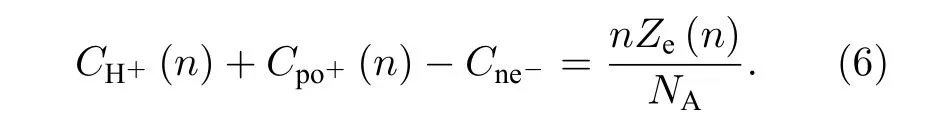
对于带负电的胶体粒子(包括本文所使用的磺酸基修饰和羧基修饰的粒子等), 只有阳离子会出现置换, 因而阴离子浓度和电解质浓度相同, 即

将(6)式和(7)式代入(5)式可得

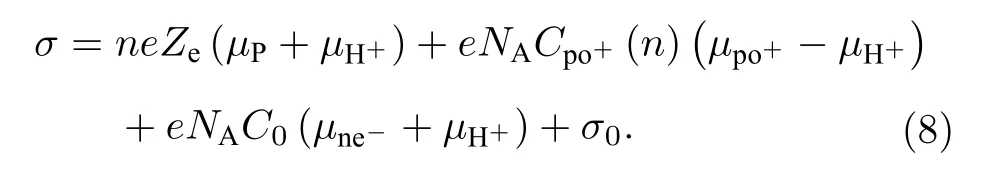
由于离子置换后的 Cpo+(n) 难以测量, 当电解质的阳离子不是H+时, 利用公式(8)难以得到粒子的表面有效电荷 Ze, 但如果电解质的阳离子为H+,尽管双电层内外仍发生H+置换, 但体系中阳离子只有H+一种, 这种情况下, 可将公式(8)化简, 即对于本文所使用的电解质HCl 的情况, 可将公式改写为

其 中, µH+=36.5×10−8m2/(V·s) ,µCl-=7.1×10−8m2/(V·s).从公式(9)可知, 如果HCl 浓度固定, 则该式右边的第二项和第三项都为常量, 如果 Ze在该浓度下与粒子数密度n 无关, 则 σ −n 曲线应为一条直线.

为了方便考虑HCl 浓度与粒子浓度的比值对电导率的贡献, 还可将公式(9)变形为单个粒子引起的电导率变化量(σ — σ0)/n 与单个粒子对应的电解质离子数NAC0/n 的关系式:[15]

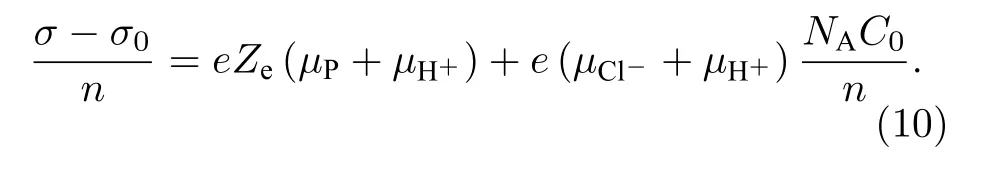
虽然(10)式是(9)式的变形, 但是在利用实验数据分析表面有效电荷 Ze的过程中, 其拟合方式是不同的, 因此两个公式得到的结果的对比可以帮助验证实验结果的准确性.另外, 该公式综合考虑了电解质浓度和数密度的耦合关系的影响, 如果表面有效电荷与粒子数密度和电解质浓度均无关, 那么对于不同的电解质浓度和粒子数密度, 所有的点都应该落在同一条直线上.因此利用该公式的分析还可以进一步明确表面有效电荷是否和离子浓度有关.

基于以上考虑, 后面两节将利用(9)式和(10)式来分析和讨论实验结果.

3.2 电导率与粒子数密度的关系

图2 给出了磺酸基/羧基修饰聚苯乙烯胶体在不同HCL 浓度下的电导率与数密度的关系曲线,对同一HCl 溶液浓度, 磺酸基修饰颗粒的电导率均与粒子数密度呈线性增长关系(图2(a)), 符合公式(9)关于表面电荷不随粒子数密度发生变化的假设, 而羧基修饰胶体颗粒的电导率随粒子数密度的变化曲线(图2(b))在某一HCl 溶液浓度下并不完全线性, 数密度较低时, 电导率增长较快, 增势逐渐减缓, 直到数密度到达某一数值后, 电导率与数密度才呈线性关系.

磺酸基修饰胶体粒子直接通过拟合的线性斜率可准确得到各HCl 溶液浓度下的表面有效电荷数值, 如表2 所示, 其结果表明, 随着HCl 的浓度增大, 粒子的表面有效电荷也随之增大, 盐浓度从2.08 × 10—6mol·L—1增加到6.92 × 10—6mol·L—1,有效电荷的大小增加了约20%.在文献[16]的聚集实验中, 聚集速率的实验结果反推了粒子的表面电荷, 盐浓度由0.15 mol·L—1增加至0.6 mol·L—1,表面有效电荷增大了约80%, 有效电荷随电解质浓度增大而增大的趋势和实验结果是一致的.因为聚集实验中的电解质浓度远远大于本文实验中的浓度, 所以其增大的比例也更大.

羧基修饰聚苯乙烯胶体颗粒电导率与数密度的非线性关系, 使得直接利用曲线的拟合斜率来求表面有效电荷数的方法并不恰当, 只能利用公式(9)对羧基修饰胶体颗粒在各数密度点的斜率进行计算, 来得到不同粒子数密度下的表面电荷, 其结果如图3 所示, 初期有效电荷数较大, 随胶体数密度的增大逐渐降低, 并最终稳定.表3 为不同电解质浓度下稳定后的表面有效电荷, 即本文所采用的实验结果.

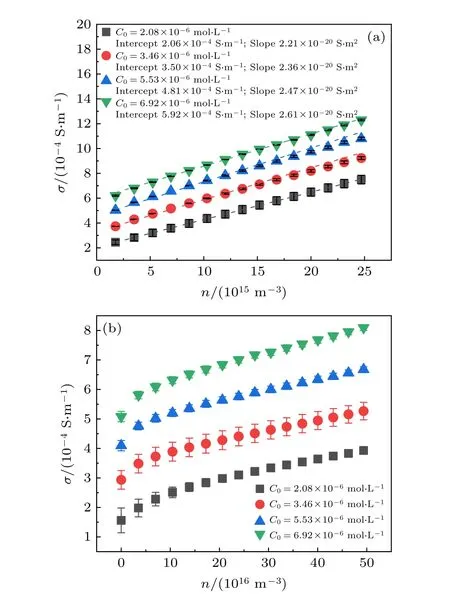
图2 (a)磺酸基和(b)羧基修饰聚苯乙烯胶体的电导率−数密度关系曲线Fig.2.Conductivity of (a) sulfonic acid and (b) carboxyl−modified polystyrene as function of the number density.

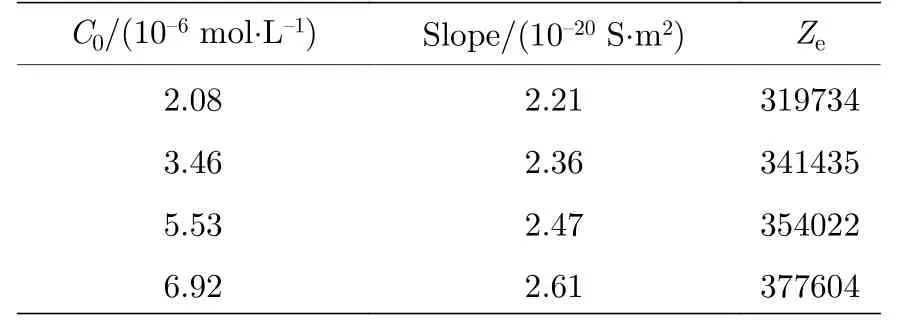
表2 磺酸基修饰聚苯乙烯胶体颗粒的σ−n 曲线斜率以及表面有效电荷数Table 2.The slope of σ−n curve and the surface ef−fective charge of sulfonic acid−modified polystyrene.

图3 羧基修饰聚苯乙烯胶体颗粒的表面有效电荷Fig.3.Surface effect charge of carboxyl−modified polystyrene.

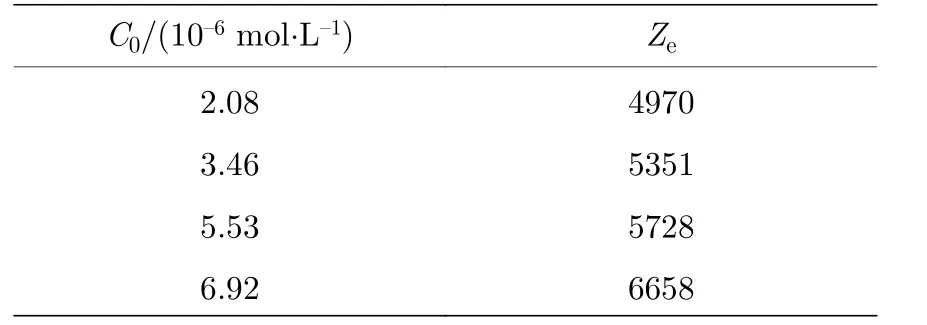
表3 羧基修饰聚苯乙烯胶体颗粒表面有效电荷数Table 3.The surface effective charge of carboxyl−modified polystyrene.

图4 磺酸基(a)和羧基(b)修饰聚苯乙烯粒子示意图Fig.4.Schematic diagram of the particles with sulfonic acid groups (a) and carboxyl groups (b).

磺酸基修饰与羧基修饰粒子的电导率与数密度关系曲线的不同表现是因为磺酸基为强酸(图4(a)), 一般认为其H+完全电离, 事实上双电层内仍有部分反离子同胶核一起运动, 故分析电荷要比有效电荷(与游离的H+有关)大[16,25].根据双电层厚度1/ κ (公式(2)), 电解质的加入使得双电层厚度被压缩[26−28], 使原本处于紧密层中随胶核一起运动的H+被部分地排挤出来, 变成可以自由移动的H+, 使有效电荷随电解质浓度增大而增大.而羧基为弱酸, 弱酸本身无法完全电离(图4(b)),加入电解质后, 电解质压缩双电层, H+从双电层内部扩散到外部, 内部H+浓度减小促进羧基电离[29].粒子浓度增大时, 外部H+浓度随之增大, 阻止H+从双电层内部向外扩散, 抑制羧基电离.随着粒子数密度增大, 电导率−数密度的斜率降低, 到一定程度后达到稳定, 电导率−数密度曲线变为线性.

通过拟合聚苯乙烯胶体颗粒表面有效电荷数与HCl 溶液浓度(图5), 在低浓度盐的情况下, 磺酸基与羧基修饰胶体颗粒的表面有效电荷随HCL 溶液浓度的变化近似线性增长.

图5 磺酸基(a), 羧基(b)修饰聚苯乙烯粒子的表面有效电荷数Fig.5.The surface effective charge of sulfonic acid−modi−fied (a) and carboxyl−modified (b) colloidal particles.

3.3 单个粒子引起的电导率变化量与单个粒子对应的电解质离子浓度关系

根据公式(10), 理论上的斜率为 e (µCl-+µH+) ,数值是6.98 × 10—26S·m2; 截距为针对实验数据, 根据公式(10)拟合的结果如图6所示, 进而得到不同电解质浓度下的直线斜率、截距以及从截距获得的表面有效电荷(表4 和表5).理论斜率和实验斜率比较接近, 通过公式(9)和公式(10)分别求得的颗粒表面有效电荷数也非常接近, 通过对比表2 和表4, 得到磺酸基修饰的颗粒的Ze和平均误差为0.64%; 通过表3 和表5 得到的羧基修饰颗粒的Ze和平均误差为5.32%.由此可见, 将粒子数密度与HCl 溶液浓度纳入表面电荷求解方程考虑范围内是合理且有效的.除此之外, 不同HCl 溶液浓度的曲线尽管很接近, 实际并不重合, 图6 也表现了这一偏移是有明确倾向性的, 并且各线的偏移差最大分别达到了22.22%(磺酸基修饰)和52.24%(羧基修饰).对于本文选取的低浓度电解质溶液来说, 该差异还是很明显的, 表明聚苯乙烯带电粒子的表面有效电荷随HCl 溶液浓度增大, 与3.1 节的结论一致.此外, 羧基修饰颗粒相比磺酸基修饰颗粒表面电荷的增幅更大, 是因为羧基为弱酸基团, 尚未完全电离, 所以双电层内H+的减少促进了羧基电离, 使得有效电荷增大的较磺酸基修饰的颗粒多.

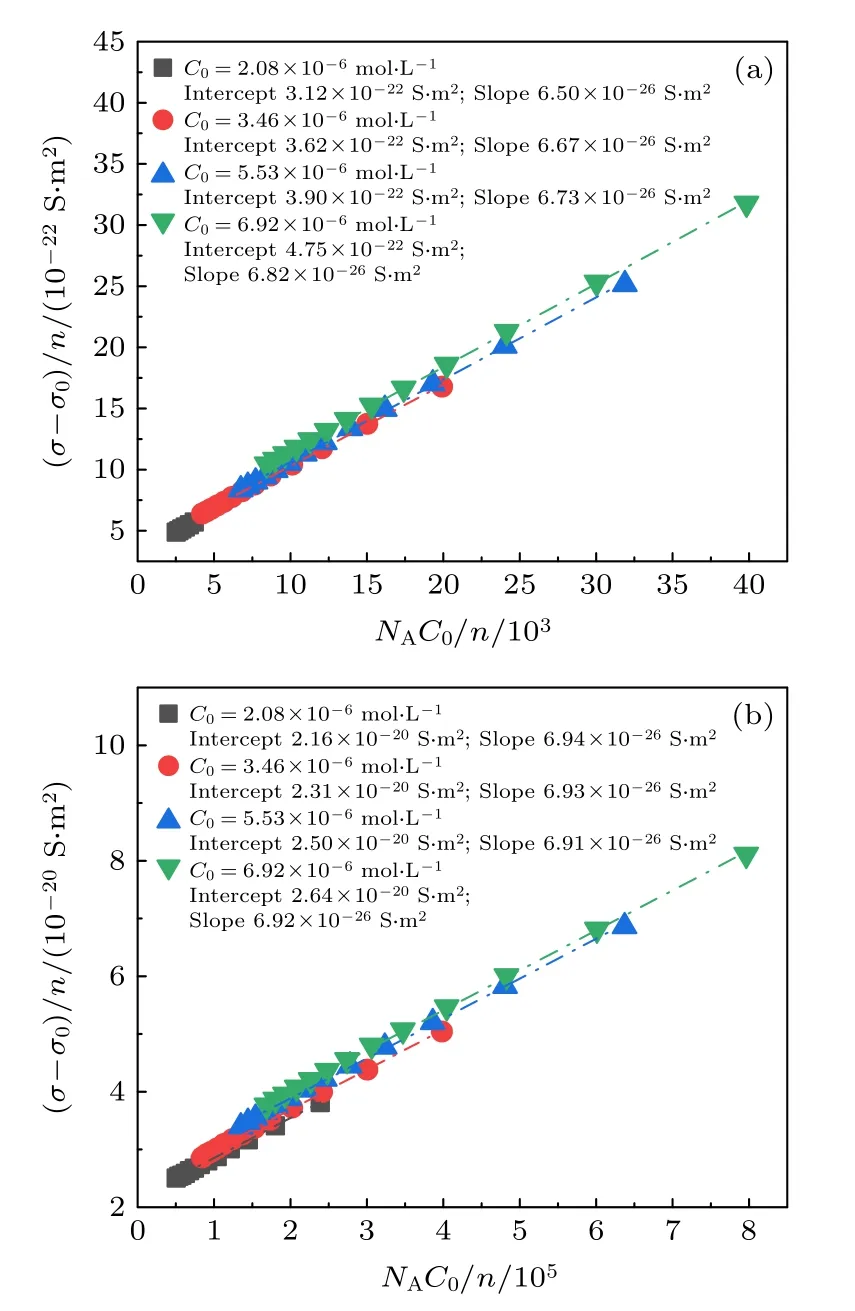
图6 磺酸基(a), 羧基(b)修饰聚苯乙烯胶体颗粒关于单个粒子引起的电导率变化量(σ-σ0)/n 与单个粒子对应的电解质离子浓度NAC0/n 关系曲线Fig.6.Conductivity contribution per particle (σ-σ0)/n as a function of the number concentration of small ions per particle NAC0/n performed on sulfonic acid−modified (a)and carboxyl−modified (b) polystyrene colloidal particles.

表4 磺酸基修饰聚苯乙烯颗粒的有效电荷Table 4.The surface effective charge of sulfonic acid−modified polystyrene.

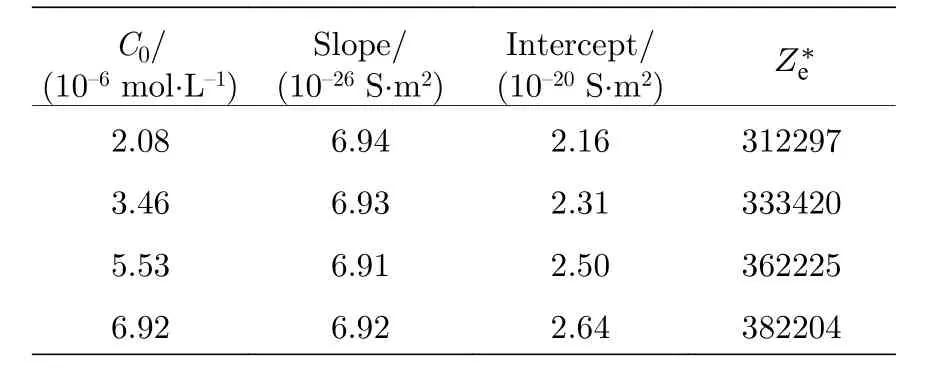
表4 磺酸基修饰聚苯乙烯颗粒的有效电荷Table 4.The surface effective charge of sulfonic acid−modified polystyrene.

C0/(10—6 mol·L—1)Slope/(10—26 S·m2)Intercept/(10—20 S·m2) Z∗e 2.08 6.94 2.16 312297 3.46 6.93 2.31 333420 5.53 6.91 2.50 362225 6.92 6.92 2.64 382204

表5 羧基修饰聚苯乙烯颗粒的有效电荷Table 5.The surface effective charge of carboxyl−modified polystyrene.

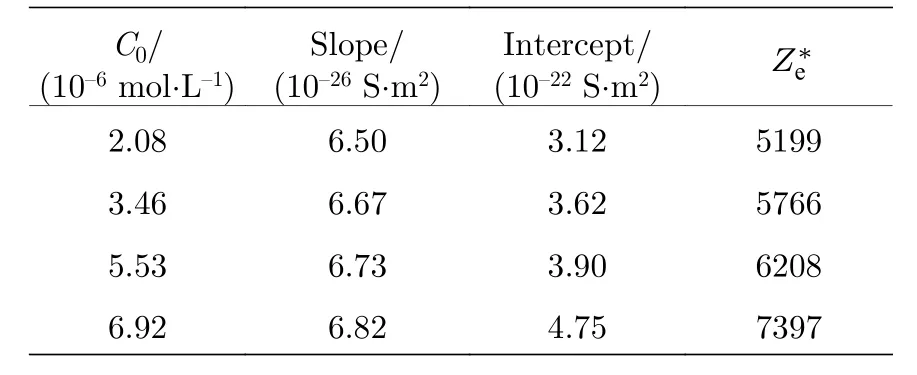
表5 羧基修饰聚苯乙烯颗粒的有效电荷Table 5.The surface effective charge of carboxyl−modified polystyrene.

C0/(10—6 mol·L—1)Slope/(10—26 S·m2)Intercept/(10—22 S·m2) Z∗e 2.08 6.50 3.12 5199 3.46 6.67 3.62 5766 5.53 6.73 3.90 6208 6.92 6.82 4.75 7397

4 结 论

本文阐述的研究工作是针对体系中电解质浓度等因素是否影响胶体粒子表面电荷的争议性问题而开展的.选用羧基和磺酸基修饰的聚苯乙烯粒子的胶体体系, 根据电导率−数密度法(迁移法)测量胶体在不同HCl 浓度下的电导率, 总结和分析电导率随胶体颗粒数密度和HCl 溶液浓度变化的规律和原因.本文研究结果表明, 修饰基团的酸性强弱不同, 颗粒数密度和盐浓度造成胶体颗粒电离平衡也不同, 两种粒子表面有效电荷数均存在随HCl 溶液浓度的升高而增大的趋势, 且弱酸修饰颗粒较强酸修饰颗粒表面电荷增多的更快.另外, 羧基修饰胶体颗粒表面有效电荷数随粒子数密度的增大而减小并趋于定值, 而磺酸基修饰胶体颗粒表面有效电荷数不随粒子数密度变化.