复杂网络牵制控制优化选点算法及节点组重要性排序*

刘慧 王炳珺 陆君安 李增扬

1) (华中科技大学人工智能与自动化学院, 武汉 430074)

2) (武汉大学数学与统计学院, 武汉 430072)

3) (华中师范大学计算机学院, 武汉 430079)

本文研究复杂网络动力学模型的无向网络牵制控制的优化选点及节点组重要性排序问题.根据牵制控制的同步准则, 网络的牵制控制同步取决于网络的Laplacian 删后矩阵的最小特征值.因此, 通过合理选择受控节点集得到一个较大的Laplacian 删后矩阵最小特征值, 是牵制控制优化选点问题的核心所在.基于Laplacian删后矩阵最小特征值的图谱性质, 本文提出了多个受控节点选取的递归迭代算法, 该算法适用于任意类型的网络.通过BA 无标度网络、NW 小世界网络及一些实际网络中的仿真实验表明: 该算法在控制节点数较少时, 能有效找到最优受控节点集.最后讨论了在复杂网络牵制控制背景下节点组重要性排序问题, 提出节点组的重要性排序与受控节点的数目有关.

1 引 言

近年来, 复杂网络上的控制与优化引起各研究领域的兴趣[1−4].在许多现实场景中, 控制一个网络的所有节点几乎是不现实的, 特别在节点数多、连接复杂的大规模网络中.为了节约控制成本, 可以通过只控制网络的部分节点并利用网络的连通性来达到控制整个网络的目的, 即牵制控制.该研究方向受到广泛关注, 并取得了许多代表性的进展.文献[5,6]提出可以通过对网络的部分节点施加控制器来实现整个网络的同步, 并研究了无标度网络的牵制控制, 发现牵制控制度大的节点比随机选点控制所需要的节点少.文献[7]提出了自适应牵制控制同步判据, 给出了网络中牵制节点的数量和耦合强度的关系式.文献[8]发现了网络在线性反馈的牵制控制下, 可以通过自适应调整耦合强度使网络达到同步.文献[9,10]从网络的图谱性质出发, 研究了复杂网络的牵制控制的能控性.其他扩展性工作还有许多, 这里不再一一赘述.上述工作主要集中在提出牵制控制同步的准则上, 没有深入研究如何选择控制节点达到网络的优化控制.至今, 牵制控制如何选择受控节点仍然是没有充分解决的问题, 需进一步理解牵制控制策略与网络结构特征的关系[11].

目前, 有一些工作从网络的拓扑度量出发给出网络牵制控制选点的策略.比如, 文献[1]提出,当网络受控节点较少时, 应当优先控制度大的节点, 当受控节点较多时, 应当优先控制度较小的节点.Wang 和Chen[5], Song 和Cao[12], 以及Ali 和Soleyman[13]研究了基于度指标的选点方案, 倾向于控制度最大的节点; Rong 等[14]、Jia 和Li[15]讨论基于介性中心度(betweenness centrality, BC)的牵制控制方案.文献[16]提出了一种基于数据流的牵制控制策略, 该策略在实际网络中可以获得与基于BC 的牵制方案相似的效果, 但计算量更小.文献[17]使用K-shell 分解法来寻找处于网络中心位置的节点, 发现K-core 值更大的节点能更有利于网络传播.文献[18]提出根据节点的森林距离大小来选择网络的控制节点, 优先选择森林距离较小的节点, 且该策略可以应用在有向网络及非连通网络中.文献[19]依据矩阵扰动理论得出推论, 可以根据Laplacian 矩阵的最大特征值对应特征向量的最大分量选择控制节点, 所得节点对网络Laplacian矩阵的特征值影响最大.但是, 这些工作都只能从某个或某些拓扑度量出发指导性地建议牵制选点方案, 或者对某类特性的网络提供针对性的建议,很难给出一个精准的方案, 在实际应用时效果不好把握.本文在我们前期工作[1]的基础上, 结合Laplacian 删后矩阵最小特征值的图谱性质, 提出了牵制控制多个节点的节点组筛选算法, 能精准地找出最优的受控节点集合.该方法不局限于特定属性的复杂网络, 对任何类型的网络都适用.

2 模型介绍及问题提出

先介绍复杂网络动力学模型, 并给出牵制控制同步准则.考虑如下具有N 个节点的连续时间动态网络模型[20], 其中网络的所有节点的自身动力学一致, 网络的状态方程描述如下:

其中i=1, 2, ···, N.在上述方程中, xi∈Rn表示节点i 的状态, f (·) 描述节点的自身动力学, 正常数c 表示网络的全局耦合强度, ui是施加在节点i 上的控制器, P ∈Rn×n是内连耦合矩阵, 它是正定或者半正定的.LN=[lij]N×N为网络的Laplacian 矩阵.本文仅考虑无向网络的情况, 即Laplacian 矩阵对角线上的元素为节点的度, 非对角线元素分别根据节点i, j 之间是否存在连边而为–1 或0.

假设网络的目标状态s(t)满足:

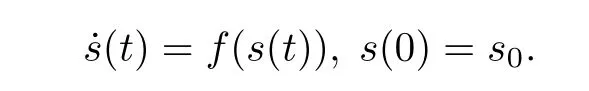
对复杂网络进行牵制控制的目的是: 通过控制网络中的部分节点, 使得网络中所有节点的状态都趋近于目标状态s(t).由文献[1]可知, 对于一个无向网络, 当选定其受控节点集时, 可以通过如下代数不等式来判别网络能否通过牵制控制达到同步,

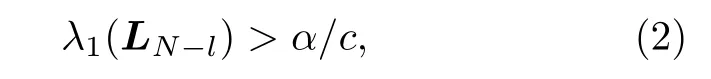
其中, l 表示受控节点个数; LN−l是网络拉普拉斯矩阵 LN删去受控节点对应行和列所得到的矩阵,即拉普拉斯矩阵的删后子矩阵, 也称为Grounded-Laplacian 矩阵[21], N–l 表示删后子矩阵的维数;λ1(LN−l)表示该删后子矩阵的最小特征值.此外,式中α 是由节点自身动力学函数 f (·) 和内连耦合矩阵P 决定的, 与网络全局耦合强度c 及网络结构无关.

接下来, 提出本文要研究的问题, 即优化(2)式左端项.当网络的受控节点数 l 给定时, 如何确定受控节点或者受控节点集, 使得被牵制控制的网络的 λ1(LN−l) 最大, 这就是牵制控制优化选点问题.然而, 寻找网络合适的受控节点集使得λ1(LN−l)最大化, 这个问题的计算量是庞大的.计算量主要来自两部分, 第一部分是计算矩阵特征值的复杂度, 第二部分是受控节点的组合数量庞大而造成的复杂度.特别是牵制控制多个节点的情况, 从所有节点中选择最优的受控节点集S ={s1,s2,··· ,sl},从而得到最大的 λ1(LN−l) , 这是一个计算量巨大的NP-hard 问题.现有的研究对于给定的受控节点数l, 仅能对可能的优化控制节点集给出宽泛建议[1].例如当受控节点数较少时, 应当优先牵制度大的节点, 当受控节点数较多时, 优先控制度小的节点; 或者仅能给出 λ1(LN−l) 的上界及下界拓扑特征估计, 并不能得到精确的最优受控节点集.本文结合删后矩阵 λ1(LN−l) 的几个特征估计式,推导出网络节点的筛选条件, 提出控制多个节点的牵制控制优化选点算法, 能够在控制节点数较少时准确找出最大 λ1(LN−l) , 并减少 λ1(LN−l) 的计算次数.

3 牵制控制优化选点算法

先介绍本文算法的理论基础及推导过程.该算法旨在筛除低价值受控节点及受控节点组合, 减少受控节点集 λ1(LN−l) 的计算, 从而以较少的计算量得出最优受控节点集.

定理1[1]假设网络拓扑结构用图G 表示.图G 的节点集为 V (G)={1,··· ,N}, 受控节点集S ⊂V , 受控节点数为l, 其中 s1,··· ,sl表示受控节点, 令 p1,··· ,pN−l表示未受控的节点, 未受控节点集表示为V/S, 并用符号 ωpj表示受控节点集S 到未受控节点 pj的连边数, 则有

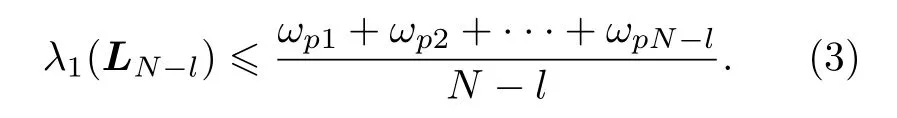
下面对(3)式进行变形, 用符号e 表示受控节点集内部连边数(即受控节点与受控节点之间的连边数), ksi表示受控节点 si的度.注意到, 有如下关系式成立:

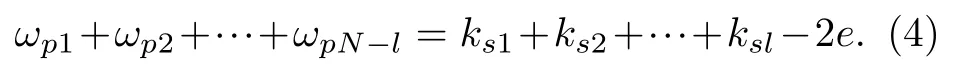
根据(3)式和(4)式可得

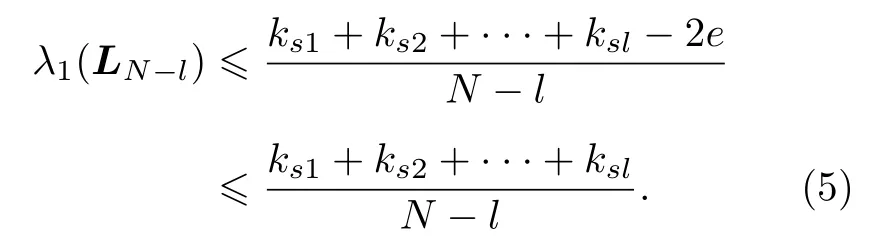
由此得到能减少最优 λ1(LN−l) 的计算次数的一个过滤条件.(5)式基于节点度进行筛选, 即寻找一个节点集, 使节点总度满足该式.而在实际网络中,对于某些度较小的节点, 即使将其搭配度最大的前l - 1 个节点, 所组成的节点集可能也无法满足条件, 因此这种度小的节点无需考虑, 这就是节点初步筛选的依据, 即节点度不满足下式的节点将直接被排除:

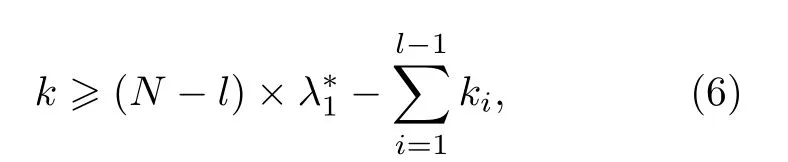
其次, 假设通过初步筛选之后剩余了n 个节点, 在这n 个节点中满足不等式(5)的节点组合,理论上有种, 从这些组合中寻找最优组合仍然计算量较大.但往往在剩余n 个节点中有大部分都是度较小的节点, 它们基本只能和度最大的节点组成满足条件(5)式的组合.根据排列组合可知,在剩余n 个节点中找到l 个满足度筛选条件的节点组合可以分为两部分: 第一部分是包含度最小节点的组合, 组合数有种, 其中w =min(l, m), m 表示当前最小度节点的个数; 第二部分是不包含度最小的节点的组合, 组合数有种.这两部分的组合数用公式表示如下:

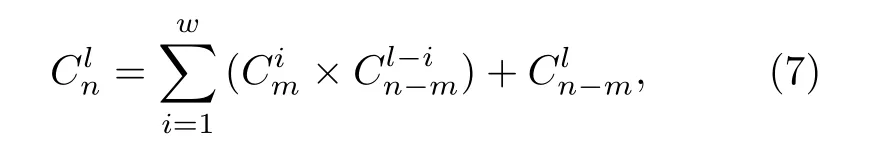
牵制控制多个节点算法最优 λ1(LN−l) 的计算算法具体实现如下: 在节点组合筛选过程中, 首先选择l 个节点作为初始受控节点, 通常选择度排序中的前l 个节点.计算控制这l 个节点的λ1(LN−l)作为筛选标准 λ∗, 根据(3)式有

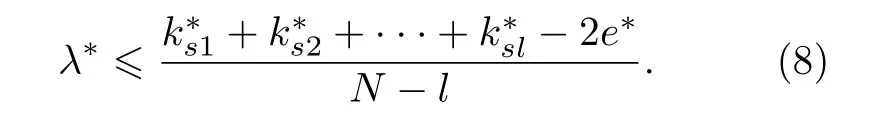
如果控制节点集 { s1,s2,··· ,sl} 要得到一个更大的 λ1(LN−l) , 即

则必须有

(10)式和(11)式即是筛选控制节点集的依据.只要在后续节点集 λ1(LN−l) 计算中得到一个更大的 λ1(LN−l) , 则将这个 λ1(LN−l) 当作新的 λ∗来筛选剩余节点集.最终对所有剩余组合计算筛选后得到的 λ∗即为最优 λ1(LN−l).

需要说明的是, 筛选条件(11)式计算简单, 仅需要知道节点的度即可.而筛选条件(10)式计算量相对大些, 还需要计算受控节点集的内部连边数, 比筛选条件(11)式准确程度更高.所以在实际仿真中, 可以结合两者实现计算复杂度和精准程度上的平衡, 也可以只采用其中的一个式子.基于以上实现过程, 现将选取多个牵制节点的算法列出如下.

算法1

步骤1选择度排名前l 的节点当作初始控制节点, 然后计算其特征值 λ1(LN−l) 作为 λ∗;

步骤2将 λ∗代入(6)式, 通过节点的度筛除不能满足(6)式的节点;

步骤3递归计算剩余节点中的满足条件(11)的节点组合;

步骤4在第3 步的基础上, 计算剩余节点中的满足条件(10)的节点组合;

步骤5逐个计算剩余节点组合对应的删后矩阵的 λ1, 如果计算出更大的 λ1(λ1>λ∗) , 则将其当作新的筛选标准, 返回第2 步继续迭代;如果未找到更大的 λ1, 则当前 λ∗即是最优 λ1(LN−l) , 当前控制节点集即是最优控制节点集.

4 实验仿真及算法有效性分析

本节将上述选点算法分别运用到生成网络如无标度网络、小世界网络, 以及真实数据网络如Email 网络、Dolphin 网络.通过数值仿真说明所提算法减少计算量的有效性, 通过与其他选点算法的对比说明算法1 相较于其他选点策略在选择λ1(LN−l)较大的节点集时更优.

4.1 算法初步应用和最优控制节点集的讨论

例1考虑参数设置为N = 1000, q = 5 的一个BA 无标度网络, 该网络以5 个节点的环状图作为初始网络, 每次增加一个新的节点, 且依照度优先连接策略连接到网络中已有的q 个节点上.生成的BA 网络见图1.根据本文的算法, 将受控节点数l 从2 增加到4, 来观察最优受控节点集的情况.节点的度排序情况见表1.

牵制控制两个节点, 即l = 2 的情况.如果枚举法需计算499500 次998 阶矩阵的最小特征值.根据算法1, 首先选择节点集合{2, 11}控节点集,计算此时的 λ1(LN−l) , 以此 λ∗=0.1986 作为初始的筛选标准, 可以得到节点{2, 11, 3, 18, 1,9, 4}满足条件(6)式, 然后依次计算节点组合的λ1(LN−l), 发现遍历所有的组合也没有得到更大的λ1(LN−l) , 则最初的 λ∗=0.1986 为最优的 λ1(LN−l) ,节点集合{2, 11}为牵制控制两个节点时的最优受控节点集合.

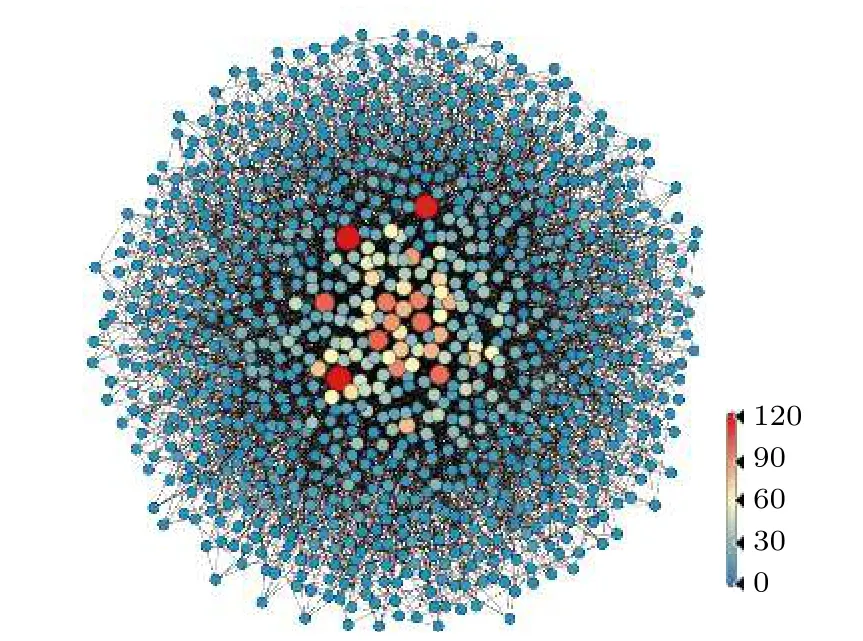
图1 生成 的BA 网 络.不同颜色代表节点的度的大小,红色表示度大的节点, 蓝色表示度小的节点Fig.1.A generated BA network.Different colors represent different node-degrees in the network; nodes in red have relative large degrees, and nodes in blue have small degrees.

牵制控制三个节点, 即l = 3 情况.如果采用枚举法需计算166167000 次997 阶矩阵的最小特征值.根据算法1, 首先选择节点集合{2, 11, 3}作为初始的受控节点集合, 计算此时的 λ∗=0.3046 ,以此 λ∗作为初始的筛选标准, 可以得到节点{2, 11,3, 18, 1, 9, 4, 8, 14, 31}满足条件(6)式, 然后依次计算节点组合的 λ1(LN−l) , 发现节点组合{2, 3,18}的 λ1(LN−l)= 0.3155 更大, 然后将此λ1(LN−l)作为新的 λ∗再进行筛选节点, 最终未能发现更大的 λ1(LN−l) , 即此时的节点集合{2, 3, 18}即为牵制控制三个节点时的最优受控节点集合.

牵制控制四个节点, 即l=4 情况.根据算法1,首先选择节点集合{2, 11, 3, 18}作为初始的受控制节点集, 计算此时的 λ∗=0.3894 , 以此 λ∗作为初始的筛选标准, 发现节点的度排序前17 的节点都满足筛选条件(6), 依次计算节点组合的 λ1(LN−l) ,发现节点集合{2, 11, 18, 9}的λ1(LN−l)=0.3963更大, 且将其作为新的筛选标准后, 没有发现更大的 λ1(LN−l) , 即此时的节点集合{2, 11, 18, 9}即为牵制控制四个节点时的最优受控节点集合.

表1 节点度排序及节点编号(BA 网络, N = 1000, q = 5)Table 1.Degree ordering and node numbering in a BA network with N = 1000 and q = 5.

从上面的实验结果可以看出, 当受控节点数由少变多时, 比如从控制3 个节点增加到控制4 个节点时, 最优受控节点组合分别是{2, 3, 18}、{2, 11,18, 9}, 优化的受控节点集合不是在控制3 个节点的优化组合上加上一个节点, 而是在原有的基础上有所删减、有所变化的节点集合.这就说明, 当受控节点数目l 增加时, 最优受控节点集不能通过贪心选点策略得出.

4.2 算法1 减少优化 λ 1(LN−l) 的计算量的有效性分析

为了客观评价本文算法减少计算量的效果, 这里给出两个指标:首次筛选剩余节点n(算法1 第二步), 度筛选后剩余节点组合R(算法1 第三步).这两个指标能体现算法1 在筛选中的效果.这两个指标的计算结果均为10 次重复实验取平均.

1) 首次筛选剩余节点数n 相关仿真结果及分析

用n 表示首次筛选（算法1 第二步）后剩余的节点数, 实验结果在表2 中列出.n 是一个重要的指标, 它很大程度决定了本文算法的计算复杂度,因为 λ1(LN−l) 理论计算次数与剩余节点n 关系很大.如果首次筛选不能将n 缩减到100 个节点左右的范围, 则待考虑的节点组合仍然会非常多, 后续的计算量比较大.简而言之, n 越小算法效果越好.由表2 可见, 随着受控节点数l 从2 增加到6,剩余节点数n 增加; 随着连边数q 减少或者连接概率P 减少, 剩余节点数n 随之增加.但实际上, 通过步骤3 计算后的剩余节点组合远小于.因为即使是通过首次筛选后的节点, 它们当中度较小的节点也占相当大的比例, 它们往往只能搭配极少数度大的节点.因此在种组合中, 绝大部分组合都不满足条件, 详细见后文剩余节点组合R 对应的实验数据.

2) 剩余节点的组合数量R 相关仿真结果及分析

用R 表示通过算法1 第三步筛选后的节点组合数量.指标R 是 λ1(LN−l) 的实际计算次数的上限, 因为即使后续组合没有计算出更大的λ1(LN−l)来实现又一轮的节点组合筛选, 也仅需将剩余组合全部计算.如果后续计算中得到了更大的 λ1(LN−l) ,并依据算法1 第二、三步再筛选掉一部分节点组合, 则计算次数将更少.从表3 中可以看到满足条件的组合数R 远小于这也说明了相比于穷举法, 本文的递归算法是有效的, 筛除了大量低价值节点组合.

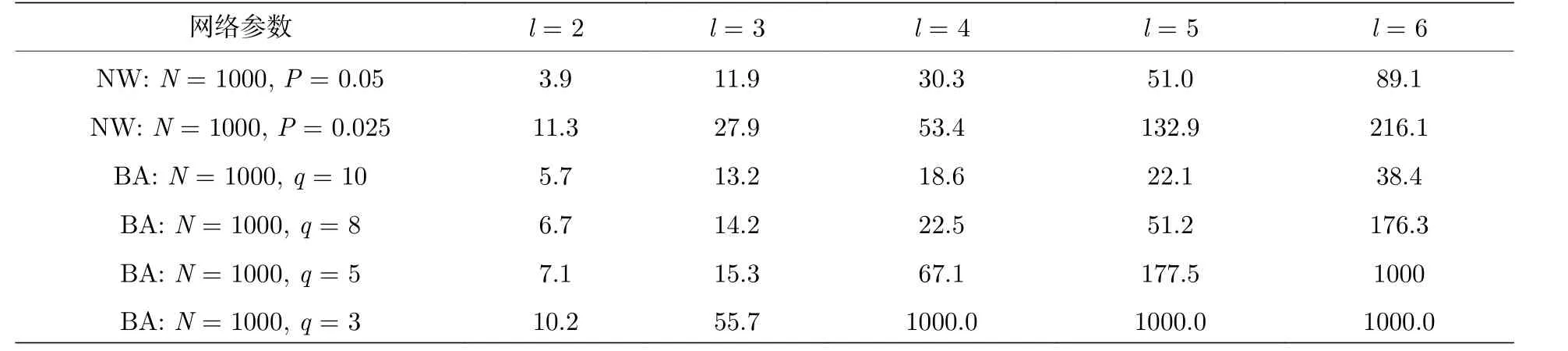
表2 通过步骤2 筛选后的剩余节点数nTable 2.Number of remaining nodes n after Step 2 in Algorithm 1.

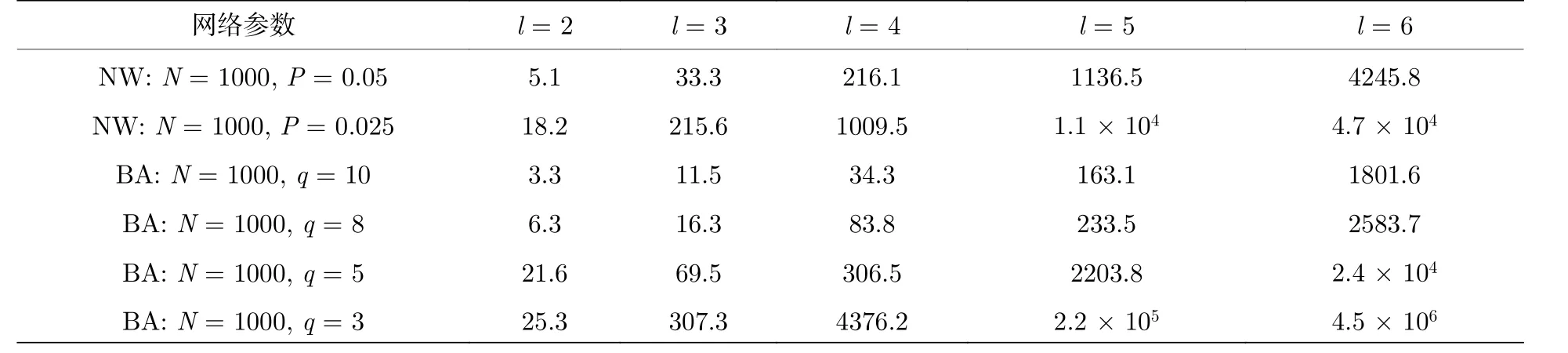
表3 通过步骤3 筛选后剩余节点的组合数量RTable 3.Number of combinations R of remaining nodes after Step 3 in Algorithm 1.

4.3 本文算法与其他选点策略的对比

本节将对当前常用牵制控制选点策略与本文算法运用在实际网络中, 进行算法选点效果的对比.首先介绍当前常用选点策略.1)度选点算法.依据节点度排序来选择受控节点, 该算法无需额外计算量, 故通常在控制多个节点时, 采用度选点算法比较方便.2) BC (betweenness centrality[14])选点策略.该策略基于介数中心度选点, 旨在找出位于网络的重要路径上的节点.3) K-shell 算法[22], 选取K-core 值大的节点.4)最近提出的基于ESI 指标的算法[19].5)本文算法, 筛选计算出最优λ1(LN−l)及受控节点.

将以上5 种策略运用在实际网络Dolphin 网络及Email 网络[23]中, 不同策略所得的选点及相应的 λ1(LN−l) 见表4 和表5 所示.表4 和表5 的实验结果表明: 本文算法得到的 λ1(LN−l) 保持最优.这验证了本文算法相比于其他算法更优.另外,把受控节点分布情况进行了可视化展示, 见图2 和图3.图中蓝色节点为未受控节点, 黄色节点(Dolphin网络中）及红色节点（Email 网络中)为受控节点,节点尺寸越大, 表示节点度越大.图2 为Dolphin网络的情况, 4 个子图(图2(a)—图2(d))给出了当受控节点数l = 5, 分别运用度算法、BC 算法、K-shell 算法、本文算法得到的受控节点分布情况.图3 给出Email 网络的情况.从上述网络选点情况可见, 度选点策略通常难以分辨节点的相对位置,而不能准确地找到最优牵制控制节点集.BC 选点策略擅长寻找到关键路径上的节点, 而这样的节点容易在一条关键路径上前后成群出现, 也不够准确找到最优牵制控制的节点集.K-shell 选点策略擅长寻找在网络中的相对中心位置的节点, 集中性强, 当节点数较多时, 对网络边缘节点控制较差.ESI 算法是根据网络Laplacian 矩阵的某个特征向量来选点, 故而其选点策略在节点的拓扑特征上不好分析, 但从实验结果发现该算法的效果不太稳定.本文所提算法能够准确计算出控制节点数量较少时的最优受控节点, 这样的节点往往度较大, 在网络中的位置也相对分散, 是牵制控制的最优节点集.

表4 不同算法在Dolphin 网络中的选点及 λ 1(LN−l) 对比Table 4.Node-selections and the corresponding λ 1(LN−l) under different algorithms on the dolphin network.

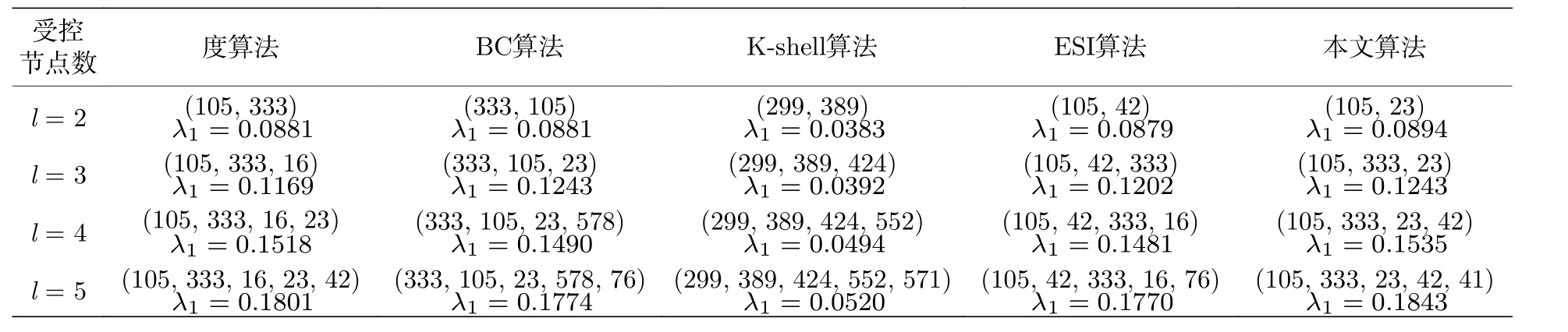
表5 不同算法在Email 网络中的选点及 λ 1(LN−l) 对比Table 5.Node-selections and the corresponding λ 1(LN−l) under different algorithms on the email network.

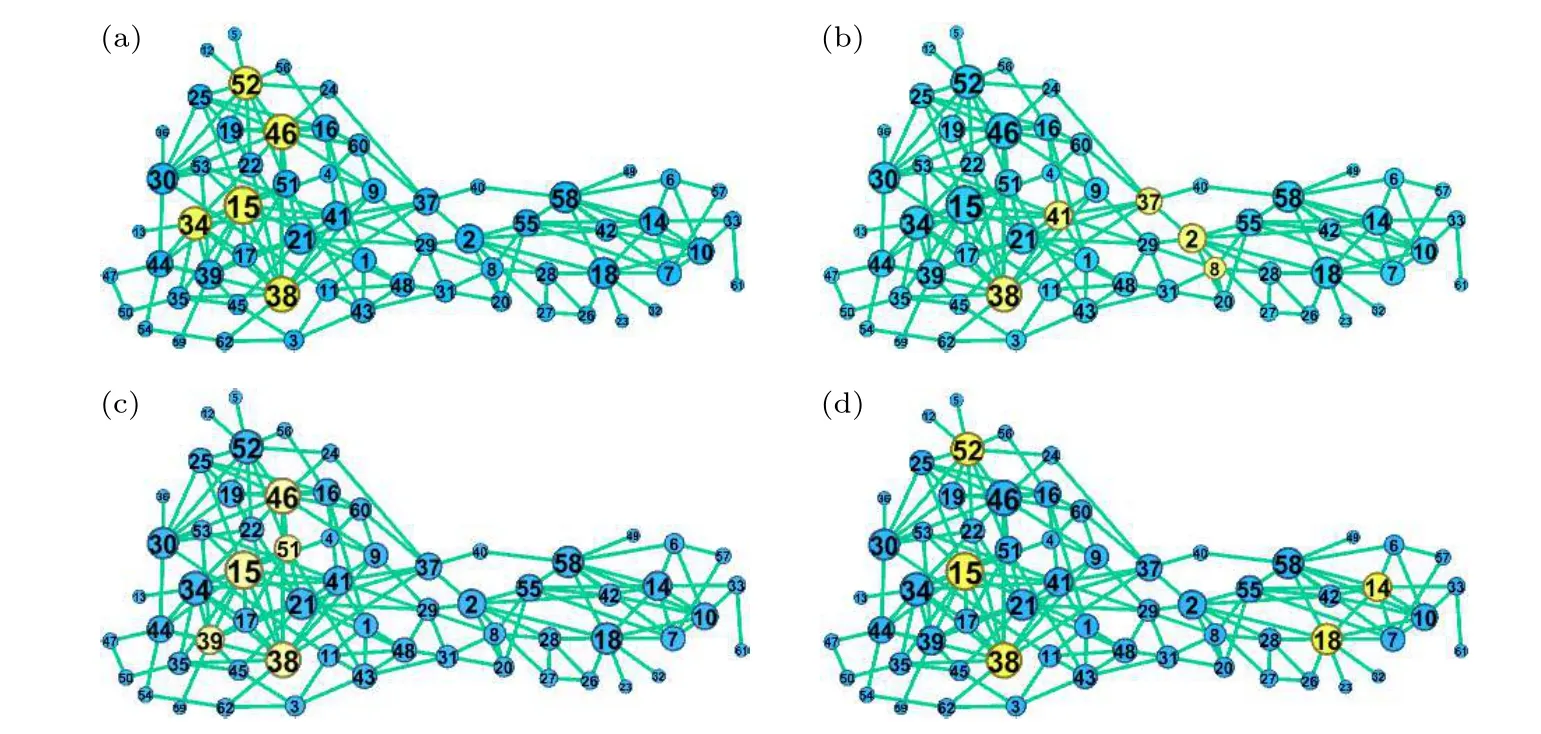
图2 在4 种不同算法下Dolphin 网络的选点情况 (a)度算法选点情况; (b) BC 算法选点情况; (c) ESI 算法选点情况; (d)本文算法选点情况Fig.2.Visualization of nodes selections on the Dolphin network underfour strategies ( l =5 ): (a) Using the degree-based pinning scheme; (b) using the BC-based pinning scheme; (c) using the ESI-based pinning scheme; (d) using our proposed algorithm.

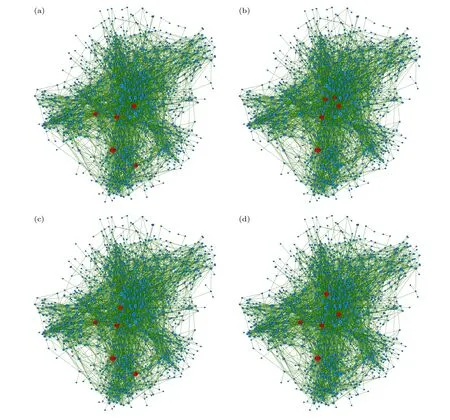
图3 在4 种不同算法下Email 网络的选点情况 (a) 度算法选点情况; (b) BC 算法选点情况; (c) ESI 算法选点情况; (d) 本文算法选点情况Fig.3.Visualization of nodes selections on the Email network under four strategies: (a) Using the degree-based pinning scheme;(b) using the BC-based pinning scheme; (c) using the ESI-based pinning scheme; (d) using our proposed algorithm.

在上述仿真中可见, 本文算法相较于其他算法, 能计算出控制节点数较少情况下（l ≤ 6）的最优控制节点集, 一定程度上填补了准确找出最优受控节点算法的空缺.但本文算法针对控制节点较多情况, 尽管能够一定程度上缩减计算量, 但剩余计算量仍然较大, 难以直接计算.

5 节点组重要性排序

如何确定网络的重要节点组, 这在现实应用场景中广泛存在.前面研究的确定网络重要节点组,实际上就是提出了一种网络节点组重要性排序方法.文献[1]提出对于无向网络确定重要节点组由网络Laplacian 删后主子矩阵的最小特征值决定;并且导出其上下界的精细估计, 指出按度大小牵制控制并不是最优方法, 牵制控制度大还是度小的节点取决于控制节点的数目; 本文给出了一定条件下删后主子矩阵最小特征值一个优化算法.

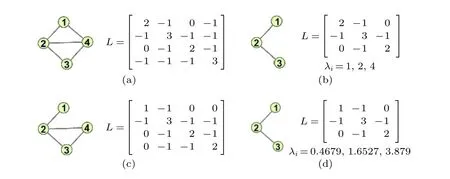
图4 两个网络A 与B 结构不同, 但删去节点4 后网络相同 (a) 网络A 及其Laplacian 矩阵; (b) 网络A 删除节点4 及其Laplacian 矩阵; (c) 网络B 及其Laplacian 矩阵; (d)网络B 删除节点4 及其Laplacian 矩阵Fig.4.The structures of networks A and B are different, but the remaining structures are the same after deleting node 4.(a) network A and its Laplacian matrix; (b) network A deleting node 4 and its Laplacian matrix; (c) network B and its Laplacian matrix;(d) network B deleting node 4 and its Laplacian matrix.

通过下面的例1 说明删后主子矩阵及其特征值蕴含了原矩阵的隐藏信息.

例1见图4, 原网络A, B 不同, 删去节点4后的网络相同, 但是删后子矩阵不同, 其特征值也不同.网络A 的删后矩阵最小特征值为1, 网络B 的删后矩阵最小特征值为0.4679.这说明了节点4 在网络A 中比在网络B 中更重要.在这个简单的例子中, 虽然删后网络相同, 但是删后主子矩阵特征值保留了原网络的隐藏信息.

下面给出一些例子说明删后矩阵最小特征值方法应用在节点组重要性排序上的有效性.

例2一个简单链状网络上的分析.见图5 所列5 个节点的链状网络.

图5 链状网络节点数N = 5 及其拉普拉斯矩阵Fig.5.Chain graph with N = 5 and its Laplacian matrix.

在该网络中, 对于一个节点的重要性排序, 节点1, 2, 3 的 λ1(LN−l) 分 别 为 0.1206, 0.1981,0.3820, 所以单个节点排序中节点3 最重要, 节点2 和4 其次, 节点1 和5 最差.对于两个节点的节点组重要性排序: 节点组(2, 4), (1, 4), (2, 5)的λ1(LN−l)=1(最重要), (1, 5)为0.5858 (其次重要), (2, 3), (1, 3), (3, 4), (3, 5)为0.3820 (较不重要), (1, 2), (4, 5)为0.1981(最不重要).这一简单例子也说明, 单个节点排序最重要的节点不一定包含在两个节点的节点组的第一位.

例3一根水平樑如何选择两个基点(l=2)将它吊起呢？假设樑长度为1, 然后作细等分（只要细分足够密, 离散网络的节点组排序可以逼近连续问题的基点选择）, 分点视为节点, 便成为N 个节点的链.设N=82, 根据对称性, 第一个基点节点从节点1—41 中选, 另一个从82—42 中选.图6 刻画了 λ1(LN−2) 与所选节点位置的关系.从图6 可以看出, 当两个节点选取(21, 62)时特征值取得最大值.当两个节点都取两端(1, 82)或中间(41, 42)时, 特征值达最小值.也就是说对于链状图最优节点接近在1/4 和3/4 的位置.例如取N = 302的链, 经计算最优节点为(76, 227), 也符合上述1/4 和3/4 的规律.

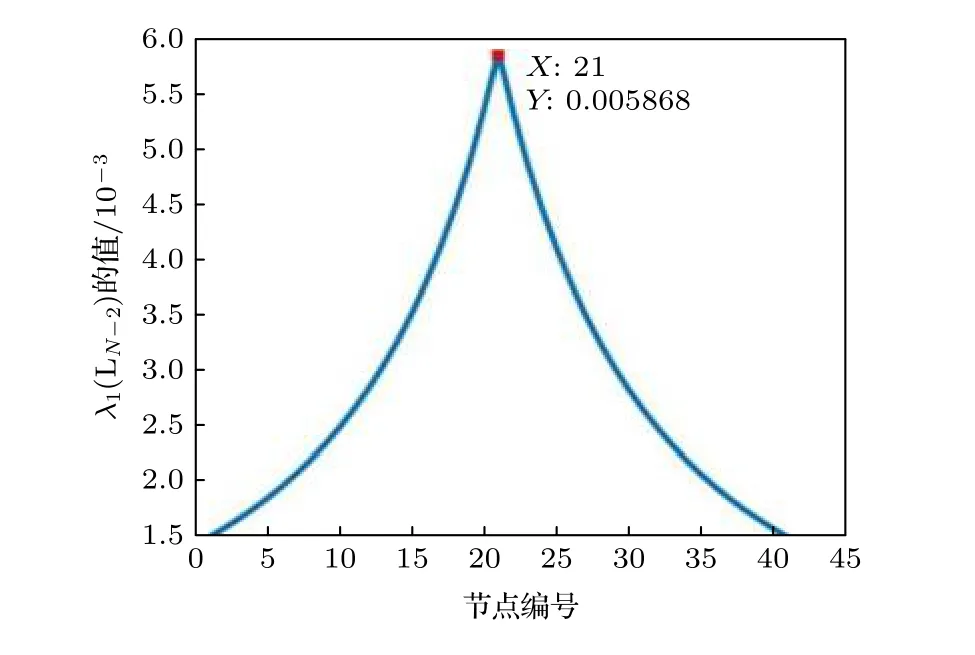
图6 λ 1(LN−2) 与左节点位置(两节点对称选取)的关系图, 这里N = 82Fig.6.The relationship of λ 1(LN−2) and the left node’s position, where N = 82 and the two nodes are selected symmetrically.

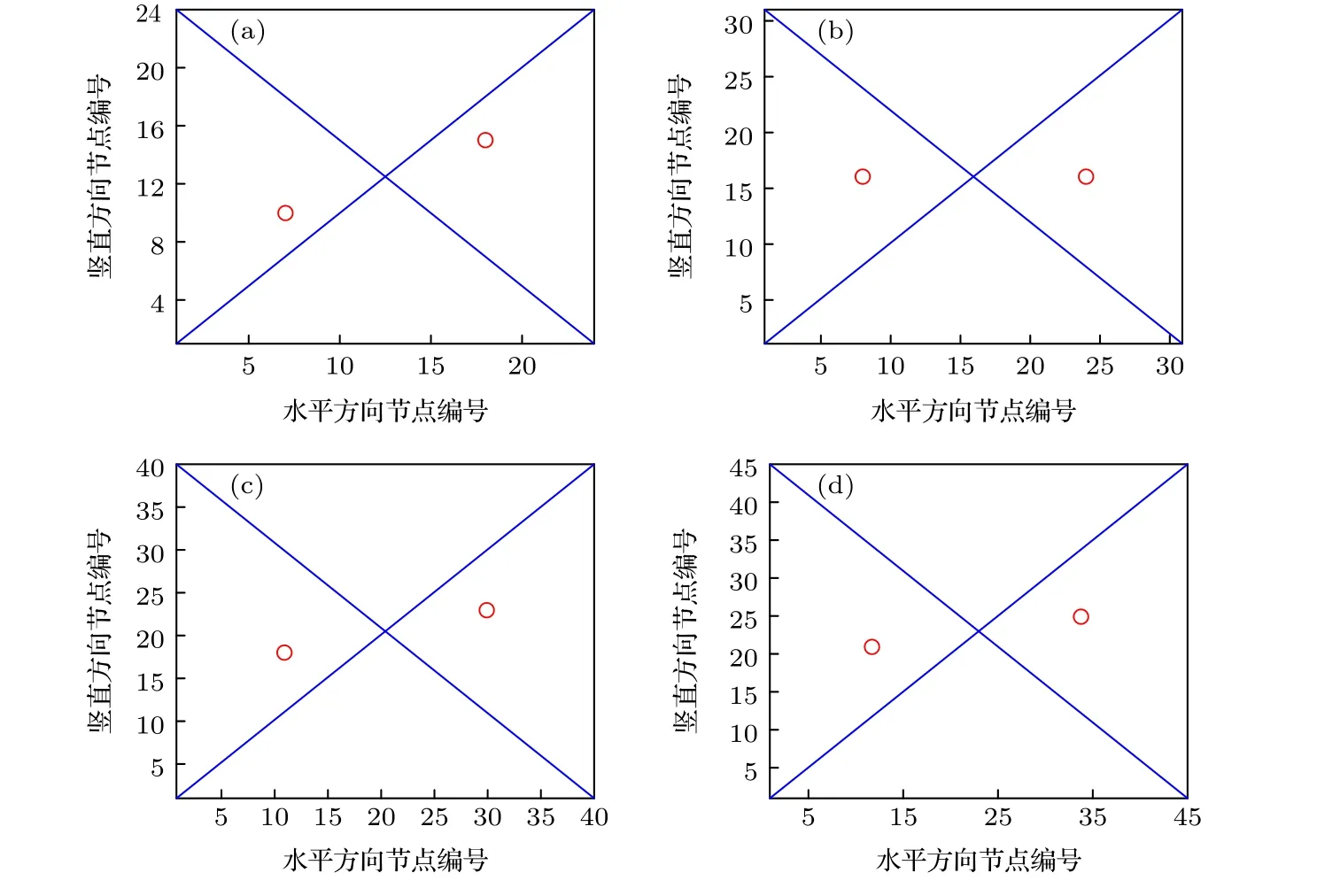
图7 在正方形网格中选两个最重要的节点, 见图中红色的点 (a) 24 × 24 的正方形网格; (b) 31 × 31 的正方形网格; (c) 40 ×40 的正方形网格; (d) 45 × 45 的正方形网格Fig.7.Pinning two nodes in a square lattice.The optimal options are shown by red nodes: (a) The square with 24 × 24 nodes;(b) the square with 31 × 31 nodes; (c) the square with 40 × 40 nodes; (d) the square with 45 × 45 nodes.

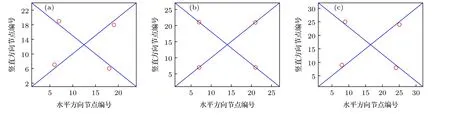
图8 正方形网络选4 个最重要的节点, 见图中红色的点 (a) 24 × 24 正方形网格; (b) 27 × 27 正方形网格; (c) 32 × 32 正方形网格Fig.8.Pinning four nodes in a square lattice.The optimal options are shown by red nodes: (a) The square with 24 × 24 nodes;(b) the square with 27 × 27 nodes; (c) the square with 32 × 32 nodes.

例4寻找正方形网络中最重要的2 个节点组成的节点组.在正方形网格中选两个最重要的节点使得 λ1(LN−2) 最大.图7 中红色的点是计算得到的最优位置.从图7 发现, 控制节点处于对称位置, 却并不一定处于对角线上.

接着, 在正方形网络中寻找最重要的4 个节点, 发现找到的最优节点组也处于对称位置, 但多数情况都不是位于对角线上, 大正方形网络分成4 个小正方形网络, 最优控制节点在4 个小正方形找中心节点偏移一格的位置上, 见图8(a)和图8(c)所示情形; 也有落在对角线上的情形, 见图8(b).

例5社团的重要性.比较三个社团在网络中的重要性, 见图9, 其中红色8 个节点, 蓝色7 个节点, 绿色6 个节点.它们的Laplacian 矩阵的删后主子矩阵最小特征值分别为0.1905, 0.1792, 0.1597,说明红色组最重要, 其次为蓝色, 最后为绿色.

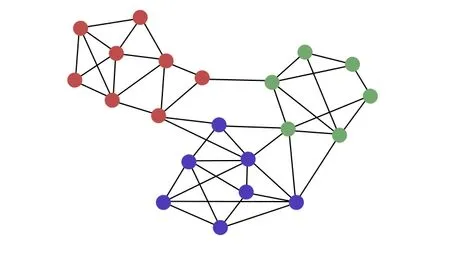
图9 比较三个社团在网络中的重要性, 图中红蓝绿色标识了三个社团, 该图取自文献[24]Fig.9.Compare the importance of three communities in a network, in which red, blue, and green colors implicit three different communities.This network is taken from Ref.[24].

6 结 论

复杂网络的牵制控制优化是一个十分有意义的研究方向.但是由于控制多个节点时的最优受控节点集的选择是一个NP-hard 问题, 如何找出最优受控节点集是一个富有挑战性的问题, 本文正是基于此开展工作.基于Laplacian 删后矩阵的图谱性质, 提出了选择最优受控节点集的算法, 该算法在受控节点数较少(小于等于6)时, 能够准确地找到最优的受控节点集合.进一步, 本文提出复杂网络节点组重要性的问题, 这与以往定义网络节点重要性不同: 本文所提出的节点组重要性, 节点的选取依赖于节点组所包含节点的数目;节点组包含节点的数目不同, 会有不同的重要节点选择方案及排序.在以后的研究中, 我们将分析牵制控制策略及节点组重要性在多层网络[25]中的情况, 并希望进一步挖掘节点组重要性在实际网络中的应用.