七年级学生对数轴上动点问题的“畏惧”成因及对策分析

李渝东 吴治新

(1.重庆市永川区兴龙湖中学校 402160；2.重庆市永川区北山中学校 402160)

就笔者所任教学校及地区来看，动点问题对于一般学生而言是一个不愿面对、甚至畏惧的一个综合问题.既然已经出现这样的现象，作为一线教师的我们就应该思考：为什么会产生这样的影响？怎样消除学生对于动点问题的畏惧感？故笔者撰写此文，以与众多一线教师、学者交流探讨.

一、学生对数轴上动点问题的“畏惧”成因分析

笔者通过对教材结构和学生面对动点问题后的心态及做法进行调查整理后发现，造成学生对数轴上动点问题的“畏惧”原因如下：

①学生在面对数轴上的点左右运动的时候，时常联想到之前学习过的相遇、追及问题.不断的讨论相遇时间、路程、速度之间的关系，甚至还牵扯多种情况讨论，故学生一时难以接受，造就一种根深蒂固的畏难心理.②对解决数轴上动点问题的方法未系统性掌握，导致大部分学生遇到此类问题时无从下手，故选择弃之.③各类型数轴上动点问题分类解决练习欠缺，例如动点个数、动点运动方向等.

笔者认为，如若解决以上问题，学生对于数轴上动点问题将不再恐惧，甚至期望遇见并解决此类动点问题.

二、解决学生对数轴上动点问题畏惧的有效策略

1.重构方法，提升自信

通过对一道例题的多解，重构解决数轴上动点问题方法步骤.

例1在数轴上，已知有B、A两点对应的数分别为3、-1，P点为一动点对应的数记为x. (如图1)

图1

问：若点A到点P的距离等于点B到点P的距离,则点P表示的数为多少？

解法1：根据题意，利用中点公式(a+b)/2代入直接求解；(其中a、b为数轴上任两点所代表的数)

解法2：根据题意，利用距离公式AB= |b-a|或|a-b|，列方程、分类求解；(其中b、a为数轴上任两点B、A所代表的数)

解法3：根据题意，利用动点公式A：a±m，结合加减运算即可求解.(其中a为数轴上点A所代表的数，m为点A在数轴上某方向移动的路程，点如果向正方向运动即加、如果向负方向运动即减)

其中在使用距离公式时有一常用技巧.我们在使用之前要明白，为何距离公式含有绝对值？原因在于距离一定为正，我们无法判断两点对应的数谁大谁小时，两数相减就无法判断距离结果为正还是为负，故加上绝对值.在解决含有绝对值的方程时，经常运用分类讨论的方法，这是学生感觉麻烦的地方，特别是需要讨论的情况过多的时候.为在某些情况下避免累赘讨论，故用到这样一个技巧：大减小一定为正，则不必加绝对值.

笔者列举此题的三种解法，正是解决动点问题的必备知识及结论，紧抓这三大法宝，就拥有了解决数轴上动点问题的底气和信心.

2.题型分类，系统解决

笔者发现，通过对七年级数轴上动点问题的分类分析，动点和距离时常综合起来考察.从动点个数的角度分为以下两类：

其一：一个点运动

其二：两个或多个点运动，又分为以下两小类：

(1)两或多个点同时运动

前提条件仍为例1所示：P点从O点向右运动，速度为5个单位长度每秒,A点向右运动，速度为5个单位长度每秒,B点向右运动，速度是4个单位长度每秒,三点同时出发按照上述速度和方向出发，多少秒后P到A和B的距离相等?(如图1)

解运用动点公式，P：0+5tA：-1+5tB：3+4t

运用距离公式及文中所提技巧，PA=5t-(-1+5t)=1,PB=|5t-(3+4t)|= |t-3)|；

根据题意令其相等，求得t，PA=PB，|t-3)| =1，得t=2或4. 故2或4秒后P到点A、点B的距离相等.

另外：一条线段动实质则为两个点同时、同向、同速运动，方法如上即可.

(2)两或多个点不同时运动

此类问题要求对动点公式A：a±m(a为数轴上点A所表示的数，m为点A在数轴上某方向移动的路程，向正方向用加、负方向用减)理解透彻，不同时运动时路程m的值如何取.

例2已知数轴上有点A对应的数为a、点B对应的数为b、点C对应的数为c,并且三点满足|a+24|+|b+10|+(c-10)2=0这一关系式，动点P从A出发,以1个单位每秒的速度向C移动,如果令时间为t秒．

(1)求a、b、c的值．(2)若PA=2PB，求点P对应的数．

(3)当P点运动到点B时,Q点开始从点A出发,以3个单位每秒的速度向点C运动, 点Q到达点C后,再以同样的速度马上返回，运动到A停止运动，在Q点开始运动后第多少秒时，P点、Q点两点的距离为4？并且说明理由. (如图2)

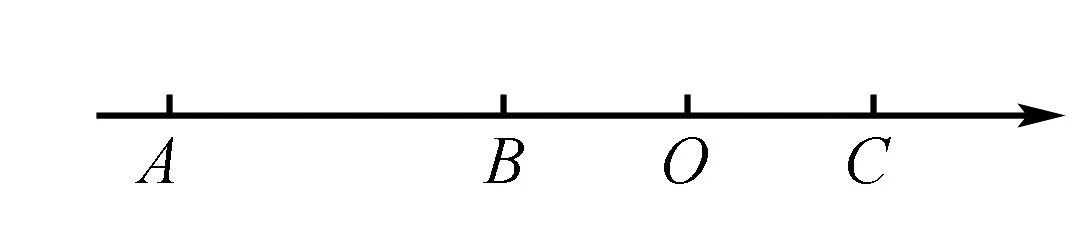
图2

解(3) 设Q点运动时间t.

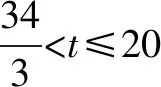
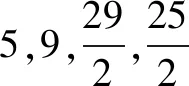
如上笔者是以动点个数进行分类，在实际教学中还可加入动点运动方向等因素，更加细致的进行分类教学.

数轴上动点问题解决方法总结为以下几点：

步骤一，运用动点公式表示动点所代表的数；

步骤二，根据具体运动情况及距离要求写出代数式并列方程；

步骤三，运用分类思想，求解含有绝对值的方程.

3.反思总结，提升历练

对动点问题学习困难的情况在一线教学中属于普遍现象.数轴中的问题数不胜数，其作为有理数的研究工具，在今后的学习中经常接触.然而在各教学问题的解决上如何正确面对和引导，是众多一线教师需要反思的问题.在实际教学中，我们要以让学生增强对学习数学的信心和兴趣，同时也应注重探究学习的方法，如本文在解决动点问题时运用到控制变量法，分类讨论法等.养成这样良好的数学学习习惯，培养学生能从客观事实中寻求真理的严谨态度.

充分利用教学活动，让学生在这一活动过程中逐渐提高发现和提出、分析和解决问题的能力，也就是理清问题成因及对策；让教师在教学过程中努力完善提升自己的教学手段和教学方法，激发和培养学生积极思考的学习态度；让每位学生在数学课上能动手做、动脑想、动口说从而落实“三会”.