线段中点与角平分线的类比学习
2021-03-11陈妹
陈 妹
(江苏省南京师范大学附属中学江宁分校 211102)
在数学学习和研究中,类比是一种重要的思想方法,也是合情推理得一种重要形式.类比是根据两个对象或两类事物的一些属性相同或相似,猜测另一些属性也可能相同或相似的思维方法,亦是由特殊到一般的过程.
一、线段中点与角平分线的概念
1.线段中点:把一条线段分成相等的两部分的点,叫这条线段的中点.
2.角平分线:从一个角的顶点引出一条射线,把这个角分成相等的两个角的,则这条射线叫这个角的角平分线.
二、单中点与单角平分线问题的类比
例1如图1,已知线段AB=10cm,在直线AB上有一点C,且BC=2cm,若点M是线段AC的中点,则线段AM=____.

图1
分析①如图1,当点C在线段AB的延长线上时,此时AC=AB+BC=12,



图2
类比1已知∠AOB=60,∠BOC=20°,若OM平分∠AOC,则∠AOM=____.
分析①如图1,当∠BOC在∠A0B外部时,此时∠AOC=∠A0B+∠BOC=80°,
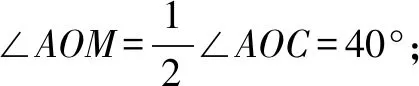
②如图2,当∠BOC在∠A0B内部时,此时∠AOC=∠A0B-∠BOC=40°,

做此题时要引导学生应考虑到A、B、C三点之间的位置关系的多种可能,即点C在线段AB的延长线上或点C在线段AB上.类比到角中,∠BOC也可以在角的内部,也可以在角的外部,对于不同的情况,要进行分类讨论.
三、双中点与双角平分线问题的类比
例2如图3,已知线段AB=10cm,C为线段AB上一点,M、N分别为AC、BC的中点,

图3
(1)若BC=4cm,求MN的长;
(2)若BC=7cm,求MN的长;
(3)若C为线段AB上任一点,你能求MN的长吗?请写出结论,并说明理由.
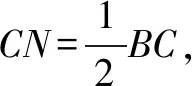

图4
类比2如图,已知∠AOB=90°,∠AOC在∠AOB的内部,OM、ON分别平分∠AOC和∠BOC,
(1)若∠AOC=20°,求∠MON的度数;
(2)若∠BOC=50°,求∠MON的度数,
(3)由(1)(2)的结果你发现了什么规律,请写出结论,并说明理由.
分析在(1)(2)两问中,由ON平分∠AOC的中点,则得

考查了两点间的距离,利用线段的中点的性质转化线段之间的和差关系是解题的关键,类比2综合考查了角平分线的定义,角的和差等相关知识,重点掌握角平分线的定义.这两题从本质上来讲,都是根据已知条件求解线段的长度或者角的度数,都是求解定值的过程,也都是由特殊到一般的过程,注重引导学生运用整体思想说理,同时要注意在不同的情况下灵活选用线段中点或角平分线的不同表示方法,有利于解题的简洁性.
例3如图5,已知线段AB=10cm,C为线段AB延长线上一点,M、N分别为AC、BC的中点,
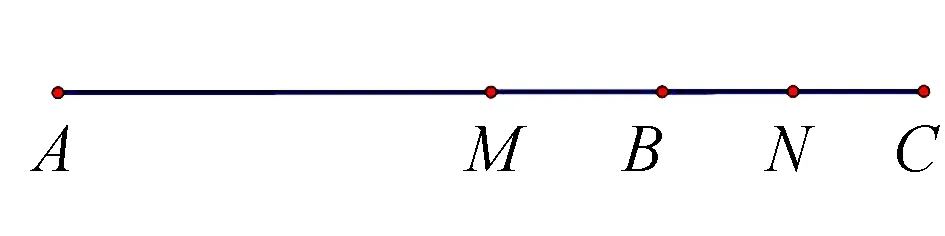
图5
(1)若BC=4cm,求MN的长;
(2)若BC=7cm,求MN的长;
(3)若C为线段AB延长线上任一点,你能求MN的长吗?若能,请求出MN的长,并说明理由.

图6
类比3如图,已知∠AOB=90°,∠AOC在∠AOB的外部,OM、ON分别平分∠AOC和∠BOC,
(1)若∠AOC=20°,求∠MON的度数;
(2)若∠AOC=50°,求∠MON的度数;
(3)由(1)(2)的结果,你发现了什么规律,请写出结论,并说明理由.
同样的,类比“例2”与“类比2”,也很容易求出这两题的一般结论.此时不妨引导学生去总结一下求双中点和双角平分线问题的一般规律.在双中点问题中的一般性结论:在同一条直线上,有公共端点两条线段中点之间的距离就等于,不重合的那两端点距离的一半.通过类比,我们可以得到在双角平分线问题中的一般性结论:当两个角的顶点及边重合时,两个角的平分线所组成的角,就应该等于不重合的两边所构成角的一半.紧扣线段的公共端点或角的公共边,从中点定义或角平分线出发,得出一般性的结论.
练习1.已知C为直线AB上任一点,M、N分别为AC、BC的中点,试探究MN与AB之间的关系,并说明理由.
2.已知∠AOB,过点O一射线OC,OM平分∠AOC,ON平分∠BOC,试探究∠MON与∠AOB的关系,并说明理由.
诚如数学家G·波利亚说:“类比是一个伟大的引路人.”在数学问题的解决中,很多数学家就是利用类比法猜想某些结论的成立,并对之进行证明,推进了数学的发展.在本文中通过对中点定义、角平分线定义在解题中应用的类比,不仅可以让学生自己得到类似知识点的概念,引导学生体会应用由特殊到一般的思想方法,探索图形中的一般规律,而且有利于在学习过程中培养勤于思考、乐于探究的学习习惯,提高学生在数学学习中的自信心和积极性.在数学学习研究中,用到的往往不是单一的思想方法,比如本文中还涉及到数形结合思想、分类讨论思想,甚至对于题目的处理也可以运用方程思想来解决.这也再次要求我们教师在平时的教学中不断渗透数学思想方法,重视培养学生的核心素养,教会学生去思考,做好学生数学学习的引路人.
